graphics - 演算法筆記

shape rendering

🗎

前言

想要畫一張複雜的圖，無論是藝術家還是數學家，都是從簡單的幾何形狀：直線、方、圓開始。本篇文章將介紹如何繪製簡單的幾何形狀。

shape rendering 的演算法已經在顯示卡上燒成電路、並且包裝成函式庫。前人種樹後人乘涼，我們大可不必痛下苦功編寫程式碼。然而本篇文章不談函式庫。

shape rendering 擁有相關的檔案格式 SVG 。然而本篇文章不談資料結構。

操控鍵盤滑鼠即時繪製圖形，我們需要了解監聽和處理事件的機制。然而本篇文章不談事件處理。

繪製直線、曲線、方形、圓形等等圖形，管理鍵盤、滑鼠、視窗等等介面，我們需要規劃編排大量程式碼。然而本篇文章不談物件導向。

shape rendering 的軟體已經發展成熟。然而本篇文章不談如何製作軟體，也不談如何使用軟體。

像素

const int X = 1024, Y = 768;
struct Color {unsigned char r, g, b;};
Color image[Y][X];
void drawPixel(int x, int y, Color c = (Color){0,0,0})
{
image[y][x] = c;
}
bool onImage(int x, int y)
{
return x >= 0 && x < X && y >= 0 && y < Y;
}
void initImage()
{
memset(image, 0xff, sizeof(image)); // 白色
}

直線

給定線段的兩個端點，如何找到線段對應的像素呢？

腦筋靈活的讀者肯定馬上聯想到一次內插。不過像素看起來零零散散的，根本沒有連成一線。

void drawSegment(Point p1, Point p2)
{
int xmin = max(0, (int)ceil (min(p1.x, p2.x)));
int xmax = min(X-1, (int)floor(max(p1.x, p2.x)));
for (int x = xmin; x <= xmax; ++x)
{
float y = (p2.x == p1.x ? p1.y : (x - p1.x) / (p2.x - p1.x) * (p2.y - p1.y) + p1.y);
drawPixel(x, round(y));
}
}

DDA algorithm 則是計算兩個端點在 X 軸、 Y 軸上的差距，取較大者作為像素數量，使得像素互相碰觸。另一方面，從逐點內插，改為預先計算斜率、逐步累加，大幅降低了運算量。

void drawSegment(Point p1, Point p2)
{
Point length = p2 - p1;
int step = ceil(max(
fabs(length.x),
fabs(length.y),
fabs(length.z)
));
Point gap = length / step;
for (int i=0; i<step+1; ++i)
{
int x = round(p1.x); // 四捨五入
int y = round(p1.y);
if (!onImage(x, y)) continue;
drawPixel(x, y);
p1 = p1 + gap;
}
}

Bresenham's algorithm 搞定了浮點數誤差。

Wu's algorithm 加入了抗鋸齒效果。

曲線

大家習慣使用 Bézier curve 。

遞推：窮舉各種參數值。相鄰控制點，反覆取加權平均數，直到得出一點。

分治法：貝茲曲線從中切開，分頭遞迴下去，直到兩端點位於相同像素。相鄰控制點，反覆取中點，以得到切開地點。

外插：以泰勒近似得到外插公式。計算速度極快，誤差稍高。

解方程式：窮舉水平線，求得水平線與曲線的交點。

void drawCurve(Point p1, Point p2, Point p3, Point p4)
{
if (fabs(p1.x - p4.x) < 1.0
&& fabs(p1.y - p4.y) < 1.0) return;
Point a1 = (p1 + p2) / 2.0;
Point a2 = (p2 + p3) / 2.0;
Point a3 = (p3 + p4) / 2.0;
Point b1 = (a1 + a2) / 2.0;
Point b2 = (a2 + a3) / 2.0;
Point c = (b1 + b2) / 2.0;
drawPixel(round(c.x), round(c.y));
drawCurve(p1, a1, b1, c );
drawCurve(c , b2, a3, p4);
}

還有加粗的貝茲曲線演算法、抗鋸齒的貝茲曲線演算法。

手繪線

其實就是一大堆的滑鼠座標位置，通常會斷斷續續不相連。

可視作 polyline 的頂點。然後套用減少頂點的演算法，甚至以 Bézier curve 作為模型。一方面平滑線條、一方面節省記憶體。

方

畫四條直線。或者視作簡單多邊形！

圓

Bresenham's algorithm 。可以推廣為橢圓和拋物線。

簡單多邊形（窮舉法）

分為空心和實心。空心很簡單，多邊形每條邊分別畫直線。

實心複雜多了。填充一個多邊形裡面所有的像素，讓整塊多邊形擁有顏色。多邊形以頂點座標的形式儲存，頂點座標是浮點數。像素座標則是整數。

最簡單的方式是試誤法：窮舉畫面上所有像素，運用「判斷點在多邊形內部」的演算法，若在內部則填色。

時間複雜度 O(XYN) 。 X 與 Y 是畫面的長與寬， N 是簡單多邊形的頂點數目。

簡單多邊形（ flood fill algorithm ）

還有沒有更好的方法呢？我們可以把問題分成兩個步驟：一、先鉤勒多邊形的邊界；二、再填充多邊形的內部。一旦有了邊界，就不必費心判斷像素是否在多邊形內。

鉤勒的部分，運用畫直線演算法即可。填墨的部分，讀者應該馬上就聯想到「 flood fill algorithm 」，遞迴往四方向填墨。

鉤勒需時 O(N+B) ，填墨需時 O(B+4A) ，總時間複雜度 O(N+B+A) 。 N 是多邊形的頂點數目， B 是多邊形邊界的像素數目， A 是多邊形內部的像素數目。

凸多邊形（ scanline fill algorithm ）

一、求出凸多邊形的最低像素和最高像素，把凸多邊形的邊，分為左邊界和右邊界。二、建立兩條陣列，陣列大小等同於凸多邊形的垂直高低差，用來儲存垂直方向各個像素的左邊界與右邊界。三、依序窮舉凸多邊形的邊，把每條邊碰到的像素位置算出來，作為邊界值，存到陣列。四、水平方向，一條一條填滿多邊形。

鉤勒需時 O(N+2B) ，填墨需時 O(2B+A) ，總時間複雜度 O(N+B+A) 。

雖然表面上 flood fill algorithm 與 scanline fill algorithm 的時間複雜度一模一樣，但是實際上 scanline fill algorithm 的速度比較快。

const int X = 1024, Y = 768;
float xmin[Y], xmax[Y];
void fillEdge(Point p1, Point p2)
{
int ymini = max(0, (int)ceil (min(p1.y, p2.y)));
int ymaxi = min(Y-1, (int)floor(max(p1.y, p2.y)));
for (int y = ymini; y <= ymaxi; ++y)
{
float x = (p2.y == p1.y ? p1.x : (y - p1.y) / (p2.y - p1.y) * (x - p1.x) + p1.x);
xmin[y] = min(xmin[y], x); // 更新左邊界
xmax[y] = max(xmax[y], x); // 更新右邊界
}
}
void fillPolygon(Polygon p)
{
float ymin = +1e9, ymax = -1e9;
for (int i=0; i<p.size(); ++i)
{
ymin = min(ymin, p[i].y);
ymax = max(ymax, p[i].y);
}
int ymini = max(0, (int)ceil (ymin));
int ymaxi = min(Y-1, (int)floor(ymax));
for (int y = ymini; y <= ymaxi; ++y)
{
xmin[y] = +1e9;
xmax[y] = -1e9;
}
for (int i=0; i<p.size(); ++i)
fillEdge(p[i], p[i+1]);
fillEdge(p.back(), p[0]);
initImage();
for (int y = ymini; y <= ymaxi; ++y)
{
int xmini = max(0, (int)ceil (xmin[y]));
int xmaxi = min(X-1, (int)floor(xmax[y]));
for (int x = xmini; x <= xmaxi; ++x)
drawPixel(x, y);
}
}

UVa 143 356

簡單多邊形（ scanline fill algorithm ）

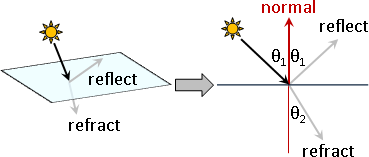
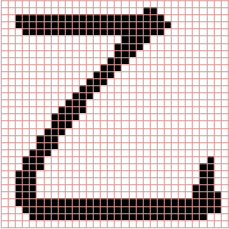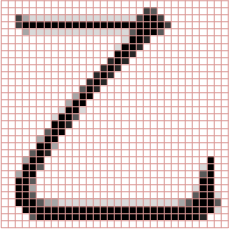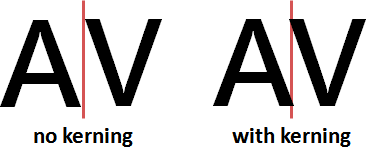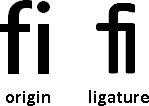font rendering

🗎

character

character 就是電腦符號。譯作「字元」或「字符」。

電腦符號都有編號。世界公定的編號方式是 Unicode 。例如第 30399 號是「算」，第 9775 號是「 ☯ 」。電腦符號包括了世界各國文字、數字、圖示、表情符號等等。

電腦符號必須編碼，節省儲存空間。 Unicode 有著 UTF-8 和 UTF-16 兩種主流的編碼方式。

字元編碼，是編碼理論的範疇。字元操作，是字串處理的範疇。字元顯示，是計算機繪圖的範疇，是我們現在要談的內容。

font

font 就是文字的造型。譯作「字體」或「字型」。

從書寫的觀點：中文字體有楷書、行書、草書、隸書、篆書五大類，有名的楷書如顏真卿、柳公權。字體是書法家發明的。

從電腦的觀點：繁體中文字型有標楷體、細明體、微軟正黑體。英文字型有 Times New Roman 、 Helvetica 、 Palatino 。字型是美術設計師和程式設計師發明的。

只要有文字的地方，通常都能更換字型，例如文字編輯器、瀏覽器、作業系統、命令提示字元。電腦可供使用的字型，主要是看你的電腦安裝了哪些字型。有專門製作字型、販售字型的公司，例如專精繁體中文字型的 JustFont 、文鼎、華康。亦有人號召製作免費開源字型，例如更紗黑體、文泉驛。

電腦顯示字元，必須透過字型。每一套字型都只替一部分的字元設計造型，例如 Times New Roman 只設計了英文字母、拉丁字母、少量的特殊符號，例如微軟正黑體只設計了英文字母、中文字、少量的特殊符號。一套字型當中，沒有設計造型的字元，就無法顯示，或者是顯示問號、空白方格等等莫名其妙的符號。儘管現今沒有任何一套字型涵蓋 Unicode 規定的所有字元，不過其實也不需要一套萬能的字型。對於沒有設計造型的字元，作業系統將另尋其他字型。

字型由作業系統控管。想要讓視窗程式顯示特定字型，土法煉鋼的方式是 Windows API ，輕鬆寫意的方式是程式語言內建的函式庫。想要讓網頁顯示特定字型，利用 CSS 的 font-family 即可。

glyph

接著到了本篇文章的主角「字形」。首先玩個小遊戲吧！拖曳控制點，按 enter 評分。美感和眼力必須很傑出。設計師的日常。

「字形」就是單獨一個字元的形狀。由演算法自動調整形狀，或由文字設計師手動調整形狀。

glyph 的資料結構

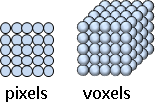
三種：點陣字 dot-matrix 、筆劃字 stroke 、輪廓字 outline 。

點陣字：用黑色方格（像素）拼成字形。

電腦已經淘汰點陣字型了，例如 Fixedsys 。然而有些字型為了支援極小尺寸，仍會搭配點陣字型，例如文泉驛點陣宋。

點陣字使用最多的地方不是電腦，而是大眾運輸的 LCD 跑馬燈。

筆劃字：直覺的方式。特別適合漢字。

記錄起點座標、終點座標、寫法（永字八法：側勒努趯策掠啄磔）（英文字母筆劃剖析）、曲率參數、變換矩陣。最後以演算法加粗筆劃，生成字型。優點是容易創造新字型，缺點是美感不佳。累死工程師、悶死設計師。

可惜的是，我們無法獲得筆劃資料。中文筆劃資料，屬於商業機密，更有專利保護。大家不得其門而入。例如王漢宗字型侵權案，個人猜測是從神秘管道得到筆劃資料，再自創加粗筆劃的演算法。

可惜的是，我們無法得知筆劃加粗的演算法。即便是開源字型，也從未公開演算法。必須跟字型公司簽技術合作。

這多少阻礙了組字、造字、文字資料庫、筆劃檢索、手寫辨識的進展。

輪廓字：公定的方式。現今字型皆是輪廓字。

輪廓由許多線條組成，線條一律是「直線線段：兩個端點」和「 Bézier curve ：兩個端點與兩個控制點」。最後以演算法填充輪廓內部，生成字型。

幸運的是，我們可以獲得輪廓資料。安裝免費開源的字形編輯軟體 FontForge ，下載免費開源的字型思源黑體、文泉驛正黑，將字形匯出成 .eps 或 .svg 檔案即得。上面的「算」就是這樣來的。

注意到，字型都有著作權，未經授權不可使用字型檔案裡面的數據，即使免費。讀者做實驗時，一定要記得選擇免費且開源的字型，以免觸法。

輪廓字的檔案格式主要有兩種：囊括所有格式的 OpenType （ .otf ）、早期的 TrueType （ .ttc .ttf ）。 OpenType 是當今主流，網路上有不少資訊。如果你有志鑽研字型渲染，可以自己寫程式存取 OpenType 檔案，也可以參考開源的字型渲染引擎 FreeType 。

em square ：字形的編輯區域

活字印刷當中， em 是指鉛字寬度。電腦字型當中， em square 是指字形的編輯區域。就這樣。

outlining ：描繪輪廓

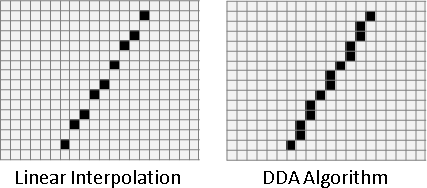
運用上個章節的繪製直線與繪製曲線演算法即可。

描繪輪廓目前沒有公定標準。即便是相同字型相同字形，在 Firefox 、 Chrome 、 Windows 、 OS X 的顯示結果通常略有不同。不同的字型渲染引擎，呈現不同結果。你也可以自己寫一個。

為了讓輪廓座標變成像素座標，這裡介紹一下 pt 和 dpi 。

電腦字型大小，單位是 pt (PostScript point) ，是長度單位。 72pt = 1 英吋， pt 除以 72 得到英吋。電腦字型通常預設 12pt 。

長度變成像素數量，單位是 dpi (dot per inch) ，每英吋多少點（像素）。電腦螢幕通常是 96dpi ，實體印刷至少是 300dpi 。

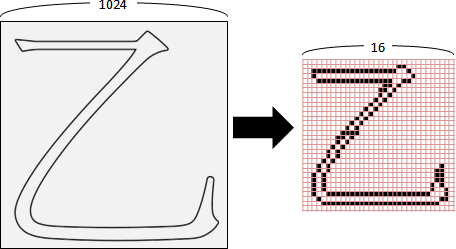
比方說， 12pt 字型， 96dpi 解析度，一個字形的邊長含有 12 ÷ 72 × 96 = 16 個像素。

假設 em square 的邊長是 1024 。輪廓座標 (x,y) ，等比例縮放得到像素座標 (round(x÷1024×16), round(y÷1024×16)) 。

filling ：填充輪廓

運用上個章節的 scanline fill algorithm 。輪廓不能交叉重疊，以利判斷內外。

如果讓輪廓具有方向性，順時針為正，逆時針為負，則得以設計聯集與差集。

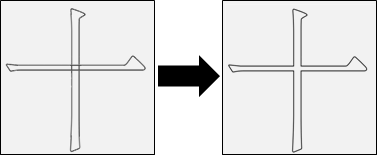
overlap removing ：重疊的輪廓，簡化成一個輪廓

為了順利填充輪廓，凡是輪廓交叉重疊，就必須重新整合。

有兩種狀況：一個輪廓自身交叉、兩個輪廓互相重疊。

需要處理的事情：求交點、求聯集或差集、重新安排頂點順序。需要的演算法：線段交點、 Bézier curve 交點、多邊形交集。不太容易實作，讀者可以挑戰看看。

字形編輯軟體有此功能，節省設計師的作業時間。

hinting / grid fitting ：微調字形位置

像素座標只能是整數。座標四捨五入變成整數，可能往左往下跑、可能往右往上跑，筆劃粗細有所改變。尤其是字形縮放大小，例如從 12pt 到 14pt ，問題更加嚴重。

像素大小固定。當字形縮小至非常小，例如 6pt ，所有筆劃通通黏結在一起。此時整個字形都得重新設計，甚至改成點陣字。

目前已經有演算法，可以自動微調字形位置。不過凡事總有例外，仍需設計師人工檢視、手動微調。各種常見縮放尺寸，都得一一檢視。中文數萬字，一字一字做，一日一日做，愚公移山、精衛填海！

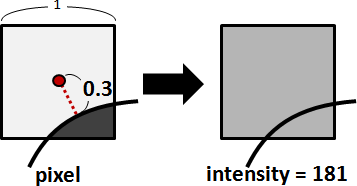
anti-aliasing ：微調字形邊緣的像素數值

在字形邊緣設定漸層顏色，使得字形邊緣柔順、清晰。

像素整齊排列。對於一條斜線，黑白顯示器，無可避免地，一定有鋸齒；灰階顯示器、彩色顯示器，則可以微調鄰近像素數值，達到平滑效果。

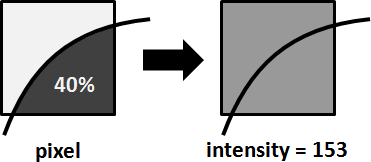
三種演算法：面積、距離、分割像素。

面積：像素視作正方形。如果字形佔據 40% 的面積，就將數值設定為 40% ，也就是 255 - (255 × 40%) = 153 。

距離：像素到輪廓的最短距離。貝茲曲線轉換成多項式，再解方程式（求根）求得最短距離。也可以用分治法。

分割像素：彩色顯示器，一個像素由 RGB 三個元件組成，調整 RGB 亮度比重，強調邊緣。缺點是邊緣五顏六色，相當刺眼，不是每個人都喜歡。知名演算法是微軟 ClearType 。

ICPC 3702

metrics ：設定字形間距

字形的部分已經介紹完畢了，接下來是排版的部分。

FreeType 的說明文件已經有精美圖片。這裡就不重畫了。

kerning ：微調字形間距

比方來說， AV 合在一起時，視覺感受是留白太多，需要更緊密一點。 AB 、 AD 不需要更緊密，保持原本排版即可。

解法是事先設定特殊組合。 OpenType 支援此設定。屬於文字處理的範疇。

另外還有一種情況，出現於阿拉伯文、泰文等等。這些語言根據語義，銜接或斷開字形。

解法是剖析語義。 OpenType 沒有此設定，由排版引擎自行實作。屬於自然語言處理的範疇。

ligature ：連合字形

比方來說， fi 合在一起時，書寫感受是筆劃太多，需要更簡潔一點，於是連合成新字形。解法同前。

專門用於程式設計的字體，也有連合功能。例如 Iosevka 、 Fira Code 、 Cascadia Code 、 JetBrains Mono ，將 != 改成 ≠ ，將 -> 改成 → 。

未涉及的主題

因為我沒有跟字型公司簽技術合作，所以知道的事情有限。

一、輪廓字的編輯介面。

二、輪廓字、筆劃字、點陣字之間的轉換。華康有個專利，演算法是迴歸。

三、拆字組字。簡化字型製作流程。

四、調字。根據環境、根據版面，自動調整字形。

五、手寫字形。工程師（詳細演算法）和設計師（詳細流程）有著不同的策略。

六、壓縮。減少字型檔案大小。例如 compact table format 和 MicroType Express 。

七、列印文字。印表機韌體設計。

font design

這是設計師的專業。已有人寫書拍片，我就不班門弄斧了。

演算法生成的字形太過呆板（例如墨字的四個點如何點）。目前的作業流程是：先由工程師產生大致輪廓，再由設計師調整細節。

繁體中文的筆劃寫法，台灣政府有訂立標準。不過政府標準不見得是好看的，也不代表是正統的。

typeface design / typography design

也許可以看看 spiro curve 、文字雲、筆劃裝飾。

math rendering

畫數學式子與畫字形，原理相同，只是還要再解決一個問題：數學式子的資料結構為何？目前最流行的方式，是用純文字記錄一道算式，所採用的文法是 TeX 的語法。

讀者可以參考 MathJax 。

web rendering

mesh rendering

🗎

這裡再提供一個更清楚的動畫。

model

將物體表面簡化成大量的平坦的多邊形，再運用「多邊形三角剖分」切割成大量的三角形，得到 mesh 。

替現實生活的物體建立 mesh ，是一套複雜的學問。所幸我們已經有現成的模型可以使用。例如此處的模型是 Utah teapot 。

mesh 由許多三角形組成。一個三角形擁有三個頂點座標（暨法向量）、正面顏色、背面顏色。

三角形的頂點順序，決定了三角形的正面：正視三角形的正面，我們習慣讓三角形頂點呈逆時針順序。依照頂點順序計算「叉積」，得到三角形的正面的法向量。這是大家約定俗成、心照不宣的規矩。

mesh 的資料結構通常是：一個陣列記錄每個點（暨法向量）、一個陣列記錄每個三角形的三個點的編號。由於三角形經常共用頂點，因此兩層式的資料結構，得以節省記憶體空間。

不過為了方便起見，以下採用笨蛋方法。

struct Triangle {Point foreColor, backColor, vertex[3], vnormal[3], normal;};
vector<Triangle> triangleList;
bool LoadFile(const char* fileName)
{
ifstream fin(fileName);
if (!fin) return false;
string s;
while (fin >> s)
{
/* 讀檔 */
Triangle t;
fin >> t.foreColor >> t.backColor;
for (int i = 0; i < 3; ++i)
fin >> t.vertex[i] >> t.vnormal[i];
/* 額外處理 */
// OpenGL的色彩值範圍是0...1，而不是0...255。
t.foreColor = t.foreColor / 256;
t.backColor = t.backColor / 256;
// 向量預先正規化，往後點積運算就不用除以向量長度。
for (int i = 0; i < 3; ++i)
t.vnormal[i] = normalize(t.vnormal[i]);
// 三角形法向量（有許多種求法，使用其中一種即可。）
t.normal = cross(t.vertex[1] - t.vertex[0], t.vertex[2] - t.vertex[0]);
// t.normal = cross(t.vertex[1] - t.vertex[0], t.vertex[2] - t.vertex[1]);
t.normal = normalize(t.normal);
if (fin) triangleList.push_back(t);
}
return true;
}

struct Point {float x, y, z;};
Point operator+(Point p1, Point p2)
{
return {p1.x + p2.x, p1.y + p2.y, p1.z + p2.z};
}
Point operator-(Point p1, Point p2)
{
return {p1.x - p2.x, p1.y - p2.y, p1.z - p2.z};
}
Point operator*(Point p, float s)
{
return {p.x * s, p.y * s, p.z * s};
}
Point operator/(Point p, float s)
{
return {p.x / s, p.y / s, p.z / s};
}
istream& operator>>(istream& in, Point p)
{
return in >> p.x >> p.y >> p.z;
}
ostream& operator<<(ostream& out, Point p)
{
return out << '(' << p.x << ',' << p.y << ',' << p.z << ')';
}
Point min(Point p1, Point p2)
{
return {min(p1.x, p2.x), min(p1.y, p2.y), min(p1.z, p2.z)};
}
Point max(Point p1, Point p2)
{
return {max(p1.x, p2.x), max(p1.y, p2.y), max(p1.z, p2.z)};
}
float dot(Point p1, Point p2)
{
return p1.x * p2.x + p1.y * p2.y + p1.z * p2.z;
}
Point cross(Point a, Point b)
{
return {a.y * b.z - b.y * a.z,
a.z * b.x - b.z * a.x,
a.x * b.y - b.x * a.y};
}
/*
float length(Point p)
{
return sqrt(dot(p, p));
}
*/
float InvSqrt(float x)
{
float xhalf = 0.5f * x;
int i = *(int*)&x;
i = 0x5f3759df - (i >> 1);
x = *(float*)&i;
x = x * (1.5f - xhalf * x * x);
return x;
}
Point normalize(Point p)
{
// return p / length(p);
return p * InvSqrt(dot(p, p));
}

UVa 10711

camera

替相機設定三個單位向量：長的方向、寬的方向、面對方向。

求得 mesh 中心點，倒退一萬步，作為焦點的位置。

// 圖片大小
const int X = 400, Y = 300;
struct Camera
{
float radius, depth;
Point dirx, diry, dirz, center, eye;
} camera;
void Camera::init()
{
// 倒退的距離不要太近也不要太遠，不然看不見整個物體。
radius = 1000;
// 圖片與焦點的距離（必須比倒退距離少）
depth = 300;
// 長的方向、寬的方向、面對方向（單位向量）
dirx = (Point){1,0,0};
diry = (Point){0,0,1};
dirz = (Point){0,1,0};
// mesh中心點
center = mesh_center();
// 焦點的位置，從物體中心倒退一萬步。
eye = center - (dirz * radius);
}
// 求得mesh中心點
Point Camera::mesh_center()
{
Point a = {+1e9, +1e9, +1e9};
Point b = {-1e9, -1e9, -1e9};
for (int i=0; i<(int)triangleList.size(); ++i)
for (int j=0; j<3; ++j)
{
a = min(a, triangleList[i].vertex[j]);
b = max(b, triangleList[i].vertex[j]);
}
return (a + b) / 2;
}

mesh rendering — camera to model

ray casting

建立焦點往像素的射線，找出第一個射中的三角形。

一、以相機的三個單位向量，建立焦點往像素的射線。

Hit Camera::cast(int x, int y)
{
// 焦點往像素的射線。（隱性轉型成float）
Point view = (dirx * (x - X/2))
+ (diry * (y - Y/2))
+ (dirz * depth);
/*
// 加上0.5，對準像素中心。此處不採用，便宜行事。
Point view = (dirx * (x - X/2 + 0.5))
+ (diry * (y - Y/2 + 0.5))
+ (dirz * depth);
*/
}

二、窮舉三角形。針對每一個三角形，以「平面與直線交點」求得交點和距離，隨時記錄最短距離。為了避免緩慢的 sqrt 運算，我們不求直線距離，而是求 dirz 方向的距離、也就是深度。

for (int i=0; i<(int)triangleList.size(); ++i)
{
Triangle& t = triangleList[i];
// 平面與直線交點
float dv = dot(view, t.normal);
float dt = dot(t.vertex[0] - eye, t.normal);
// 三角形與視線平行，距離無限大。
// 其中三角形與視線共面時，當作是太薄了看不見。
if (dv == 0) return 1e9;
// 以點積求得dirz方向的距離。dirz已經是單位向量。
float z = dot(view * dt / dv, dirz);

最後一行程式碼可以簡化。 * dt / dv 可以提到 dot 外面。 view 是由 dirx 、 diry 、 dirz 組成，這三個向量互相垂直； view 投影到 dirz 上，不需要看 dirx 和 diry ，只需要看 dirz 方向有多少投影量，點積結果顯然是 depth 。

float z = dt / dv * depth;

depth 是定值。有些人為了加速，甚至不乘上 depth ，只求倍率。倍率 1.0 剛好位於圖片上。

float z = dt / dv;

以倍率輕鬆求得交點。

float z = dt / dv;
Point hit = eye + (view * z);

三、以「判斷點在凸多邊形內部」，判斷交點是否在三角形內部。三維版本，叉積改為三重積，三角形面積改為四面體體積。

// 擊中的三角形、交點、深度、擊中正面或反面。
struct Hit {Triangle t; Point hit; float z; bool side;};
Hit Camera::cast(int x, int y)
{
// 預設沒有擊中三角形
Hit ans = {-1, eye, 1e9, true};
// 焦點往像素的射線
Point view = (dirx * (x - X/2))
+ (diry * (y - Y/2))
+ (dirz * depth);
// 焦點與三角形距離，投影到dirz上的長度。即深度。
// 目標是找到距離最短的。（已簡化成倍率）
float zvalue = 1e9;
// 窮舉所有三角形，判斷三角形與射線相交。
// 找到第一個射中的三角形。
for (int i=0; i<(int)triangleList.size(); ++i)
{
Triangle& t = triangleList[i];
// plane-ray intersection
float dv = dot(view, t.normal);
float dt = dot(t.vertex[0] - eye, t.normal);
if (dv == 0) continue;
float z = dt / dv;
if (!(z > 0 && z < zvalue)) continue;
Point hit = eye + (view * z);
// point in triangle test
Point v0 = t.vertex[0] - hit;
Point v1 = t.vertex[1] - hit;
Point v2 = t.vertex[2] - hit;
float c2 = dot(cross(v0, v1), t.normal);
float c0 = dot(cross(v1, v2), t.normal);
float c1 = dot(cross(v2, v0), t.normal);
if (c0 < 0) c0 = -c0, c1 = -c1, c2 = -c2;
if (!(c0 > 0 && c1 > 0 && c2 > 0)) continue;
// 確定擊中三角形，更新深度。（已簡化成倍率）
zvalue = z;
// 儲存結果
ans = (Hit){t, hit, z, dv < 0};
}
return ans;
}

ray casting: bounding volume hierarchy

若想加速，將所有三角形存入「 bounding volume hierarchy 」資料結構，依照區域分類所有三角形。

若想繼續加速，每個像素平行計算。實務上是運用顯示卡的 GPU ，撰寫 CUDA 程式碼，大幅加速。

struct Box {Point a, b;};
Box operator+(Box b1, Box b2)
{
return (Box){min(b1.a, b2.a), max(b1.b, b2.b)};
}
// 判斷射線是否穿過bounding box。
// 由於浮點數誤差，我們只能用複雜的方式，
// 判斷射線是否打中bounding box的六個表面。
#define check(x, y, z) \
if (view.x != 0) \
{ \
t = (box.a.x - eye.x) / view.x; \
y = eye.y + view.y * t; \
z = eye.z + view.z * t; \
if (box.a.y <= y && y <= box.b.y \
&& box.a.z <= z && z <= box.b.z) \
return true; \
\
t = (box.b.x - eye.x) / view.x; \
y = eye.y + view.y * t; \
z = eye.z + view.z * t; \
if (box.a.y <= y && y <= box.b.y \
&& box.a.z <= z && z <= box.b.z) \
return true; \
}
bool RayBoxIntersect(Point eye, Point view, Box box)
{
float x, y, z, t;
check(x, y, z);
check(y, z, x);
check(z, x, y);
return false;
}
// 本來應該是放在struct BVH裡面的變數，
// 由於C++限制太多，只好改成全域變數，方便使用。
vector<Box> box;
vector<Point> center;
bool cmpx(int i, int j) {return center[i].x < center[j].x;}
bool cmpy(int i, int j) {return center[i].y < center[j].y;}
bool cmpz(int i, int j) {return center[i].z < center[j].z;}
const int bvh_limit = 1;
vector<int> idx;
vector<Box> bvhbox;
struct Hit {Triangle t; Point hit; float z; bool side;} ans;
struct BVH {Point eye, view;} bvh;
void BVH::init()
{
int N = triangleList.size();
idx.resize(N);
box.resize(N);
center.resize(N);
bvhbox.resize(N * 4);
for (int i=0; i<(int)triangleList.size(); ++i)
{
Triangle& t = triangleList[i];
idx[i] = i;
box[i] = (Box){
min(t.vertex[0], t.vertex[1], t.vertex[2]),
max(t.vertex[0], t.vertex[1], t.vertex[2])
};
center[i] = (box[i].a + box[i].b) / 2;
}
build(1, 0, N-1);
}
void BVH::build(int o, int L, int R)
{
Box b = box[idx[L]];
for (int i=L+1; i<=R; i++)
b = b + box[idx[i]];
bvhbox[o] = b;
if (R-L+1 <= bvh_limit) return;
Point d = b.b - b.a;
if (d.x >= d.y && d.x >= d.z)
sort(idx.begin()+L, idx.begin()+R+1, cmpx);
else if (d.y >= d.z)
sort(idx.begin()+L, idx.begin()+R+1, cmpy);
else
sort(idx.begin()+L, idx.begin()+R+1, cmpz);
int M = (L + R) / 2;
build(o*2, L, M);
build(o*2+1, M+1, R);
}
void BVH::query(int o, int L, int R)
{
if (!RayBoxIntersect(eye, view, bvhbox[o]))
return;
if (R-L+1 > bvh_limit)
{
int M = (L + R) / 2;
query(o*2, L, M);
query(o*2+1, M+1, R);
return;
}
for (int i=L; i<=R; i++)
{
Triangle& t = triangleList[idx[i]];
// plane-ray intersection
float dv = dot(view, t.normal);
float dt = dot(t.vertex[0] - eye, t.normal);
// if (dv >= 0) continue; // backface culling
if (dv == 0) continue;
float z = dt / dv;
if (!(z > 0 && z < ans.z)) continue;
Point hit = eye + (view * z);
// point in triangle test
Point v0 = t.vertex[0] - hit;
Point v1 = t.vertex[1] - hit;
Point v2 = t.vertex[2] - hit;
float c2 = dot(cross(v0, v1), t.normal);
float c0 = dot(cross(v1, v2), t.normal);
float c1 = dot(cross(v2, v0), t.normal);
if (c0 < 0) c0 = -c0, c1 = -c1, c2 = -c2;
if (!(c0 > 0 && c1 > 0 && c2 > 0)) continue;
ans = (Hit){t, hit, z, dv < 0};
}
}
Hit BVH::cast(Point eye, Point view)
{
this->eye = eye;
this->view = view;
ans = (Hit){-1, eye, 1e9, true};
query(1, 0, triangleList.size()-1);
return ans;
}

UVa 12312

繪製三角形！

此處的模型是 Cornell box 。運用 OpenGL 建立視窗，將模型畫在圖片上。

窮舉每個像素，建立焦點往像素的射線；窮舉每個三角形，找出第一個射中的三角形，取得三角形顏色。

void display()
{
// 清空所有像素
glClear(GL_COLOR_BUFFER_BIT);
// 窮舉所有像素
for (int x = 0; x < X; ++x)
for (int y = 0; y < Y; ++y)
{
// 取得像素顏色
Hit h = camera.cast(x, y);
// 判斷焦點面對三角形的正面還是背面
Point color = h.side ? h.t.foreColor : h.t.backColor;
// 一個一個像素慢慢畫，不使用進階的OpenGL函式。
glColor3f(color.x, color.y, color.z);
glBegin(GL_POINTS);
glVertex2f(x, y);
glEnd();
}
// double buffering
glutSwapBuffers();
}
// 設定視窗座標系統
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei)w, (GLsizei)h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluOrtho2D(0, w, 0, h);
}
// 讀檔、設定視窗、設定繪圖細節
int main(int argc, char **argv)
{
const char fileName[] = "csie.tri";
bool load = LoadFile(fileName);
if (!load) cout << "Cannot open: " << fileName << endl;
camera.init();
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB);
glutInitWindowSize(400, 300);
glutInitWindowPosition(100, 100);
glutCreateWindow("Mesh Rendering");
glClearColor(0., 0., 0., 0.);
glShadeModel(GL_SMOOTH);
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutMainLoop();
return 0;
}

相機、矩陣、圖片函式庫，三種不同的座標系統，必須小心。

Point color[X][Y];
void make_image()
{
// 調整迴圈
for (int y = Y-1, i = 0; y >= 0; --y, ++i)
for (int x = 0, j = 0; x < X; ++x, ++j)
{
Hit h = camera.cast(x, y);
image[i][j] = h.side ? h.t.foreColor : h.t.backColor;
}
}

mesh rendering — illumination

illumination

直接取用三角形的原始顏色，外觀呆板，缺乏層次。真實世界，顏色繽紛，是因為光線照射。現在我們要引進一套光線系統，讓三角形華麗動人、閃閃發光！

一、 light 。光線的來源。

二、 optics 。光線射中物體之後，物體影響光線的機制。

三、 material 。光線射中物體之後，光線亮度與彩度變化。

四、 ray tracing 。追蹤光線軌跡。運算量最大的地方。

五、 sampling 。設定光線數量、方向，使圖片外觀柔順。

這套光線系統源自物理，源自人類對於世界現象的觀察。如果你熟悉物理理論、擅長物理實驗，可以創造更細膩的方式。

light

point light (omni light)：點光源。例如燭火、燈泡。
cone light (spotlight)：圓椎光源。例如聚光燈。
directional light (collimated light)：有向光源。例如遙遠的太陽。

area light：區域光源。光源們組成一大片面積。
model：物體當作光源，表面發光。
environment light：環境光源。光源們組成球面，包覆在場景外圍。

實際範例請見此。數量、位置、方向、亮度、彩度，五個要素。光源還可進一步組成面，添增變化。

妥善設置光源，精心營造氣氛。甚至可以實地拍攝天空的照片作為光源，諸如朝霧夕霞、天光雲彩，營造真實感。

optics

emission：發光。例如螢光棒。
absorption：吸收。日常生活常見物體都是。

reflect：反射。例如鏡子、水中倒影。
refract：折射。例如魚缸、晶鑽。
scatter：散射。例如葉隙光、雲隙光、頭髮。
diffract：繞射。很少見。

物體影響光線。或者簡單想成：光線碰撞物體，產生變化。

光波有兩個要素：頻率（彩度）和振幅（亮度）。

一道光通常由大量頻率組成，各種頻率有各種振幅。物體影響光線，不會改變頻率，而會改變各種頻率的振幅大小、行進方向。

發光吸收是振幅大小變化，反射折射散射繞射是行進方向變化。

optics 的數學模型

一、考慮反射角（等於入射角）、折射角（根據介質係數）。入射折射反射都在同一平面。適合當作業。

Point reflect(Point v, Point hit, Point normal)
{
return normal * (dot(v, normal) * -2.0) + v;
}
Point refract(Point v, Point hit, Point normal,
float index1, float index2)
{
Point nv = normalize(v);
float r = index1 / index2; // ratio of refractive index
float c = -dot(nv, normal); // cos(θ1)
// hit backface (can intergrate to the last line)
if (c < 0) {c = -c; normal = -normal;}
float d = 1.0 - r * r * (1.0 - c*c); // cos²(θ2)
// total internal reflection
if (d < 0) return (Point){0,0,0};
return (nv * r) + (normal * (r * c - sqrt(c2)));
}

二、考慮各種反射方向、折射方向。此模型稱作 BSDF = BRDF + BTDF 。雖然光線遵守物理定律、光線隨從明確軌跡，但是混雜了大量複雜結果，才是人類視覺觀感：光線不是一條而是一束，照射處不是一點而是一塊，介面不是一個平面而是很多曲折，射出不僅一個方向而是很多方向。例如虹彩。

三、考慮地點差異。此模型稱作 BSSRDF 。光線在介質內不斷散射，從別處散逸而出。光線的散射、粒子的擴散，兩者有著異曲同工之妙。距離交點越遠，射出機率越小，近似常態分布。亦可想成表面套用 Gauss filter 。例如濁液、皮肉、頭髮。

四、考慮時間差異。光線被介質吸收，緩緩射出。例如磷光、螢光。

五、考慮各種頻率。白光反射時，部分頻率消失（光的吸收）；白光折射時，各種頻率錯開（光的色散）。接近真實了。例如 dichroism 、 pleochroism 。

考慮越多，運算量、記憶量越大。四和五，當今硬體設備難以即時實現，除非取巧。

material

人類視覺透過複雜機制，揉合振幅和頻率，得到顏色。

工程師便宜行事，將光的要素，從頻率和振幅，換成顏色和亮暗程度。再瞎掰出：顏色 × 亮暗程度 = 呈現顏色。儘管不切實際，但是容易計算。

工程師便宜行事，反射光、折射光，顏色不變動，亮暗程度才變動。一種入射方向，擁有多種反射方向、折射方向，每種方向各有亮暗程度。方向以經緯度表示，亮暗程度以函數表示。函數有形容詞。

  diffuse / matte：漫射。霧面、粗糙表面。
                   反射光分散，朝不同方向。例如路面、牆壁、紙張。
specular / glossy：鏡射。鏡面、光滑表面。
                   反射光集中，朝同一方向。例如金屬、塑膠、磁磚。

給定一種材質，有物理儀器可以測量函數。採用實體的測量數據，便可模仿真實世界。已經有人收集測量數據、製作觀看軟體。

除了採用實體的測量數據，亦可採用虛擬的數學模型。現今已有多種數學模型，各有不同視覺效果。

ray tracing

一、光線接觸介面才有變化，產生反射折射。適用固體，例如居家擺設。演算法原理類似狀態空間搜尋。

   ray tracing: 焦點出發。
                光學：僅考慮反射角、折射角。
  path tracing: 焦點出發（亦可焦點和光源雙向出發）。
                光學：考慮各種反射方向、折射方向。
     radiosity: 光源出發，走K步，每步皆留下一些光子。
                焦點出發，走一步，以附近光子數量，決定像素亮度。
               （實作：每步結束後，另走一步到焦點，累加像素亮度。）
               （I^1 + I^2 + I^3 + ... + I^k）
photon mapping: 光源出發，走一步，留下一個光子。
                焦點出發，走K步，以附近光子數量，決定該步的光線亮度。

一、從焦點、光源出發，持續反射、折射，追蹤光線軌跡。
　　每次接觸介面當作一步。
二、從焦點出發時，每一步窮舉所有可能的入射方向。
　　從光源出發時，每一步窮舉所有可能的出射方向。
　　由於不可能完全窮舉，所以採用取樣，後面章節會介紹。
三、焦點、點光源僅有一點，通常瞄不準、追蹤不到。
　　因此最後一步必須無視物理定律，刻意走向焦點、點光源。(global illumination)
　　區域光源則無此問題。
四、為了減低計算量，通常只走K步。
　　又為了減少bias，以固定機率決定要不要走下一步。(Russian roulette)
　　又為了增加實感，累計一步、兩步、……、K步的結果。

// 模型全部都是球，不是mesh。
http://kevinbeason.com/smallpt/

二、光線接觸介質即有變化，於介質中不斷反射折射散射。適用氣體液體，例如雲霧、牛奶。依照濃度不同，有著各種演算法，但是皆昧於物理事實。

稀薄：視作濾心。穿過越多介質，亮暗程度變化越大。
　　　以介質厚度當作亮暗變化程度。
中等：視作粒子。氣體處處都是完美漫射。光線為直線，只散射（轉折）一次。
　　　窮舉視線的每一個位置，嘗試轉折至光源。
濃稠：視作固體。光學模型：考慮入射、出射地點差異。
　　　測量BSSRDF，套用固體的演算法。

ray tracing 的常見伎倆

    ambient occlusion: 遮光。擋住光線，產生陰影。
                       例如鼻翼的陰影、門縫。
subsurface scattering: 透光。光線於半透明介質內散射，深層與淺層的光線重疊。
                       例如白裡透紅的肌膚、透光的窗簾、濁液、葉片、玉。

soft light/shadow: 柔光、柔影。
從交點發出大量射線，判斷打中多少光源，決定亮度。
volumetric light/shadow: 光芒、陰暗。例如百葉窗散落的光、積雨雲散落的陰影。
從光源發出大量光線。再從焦點發出大量射線，判斷打中多少光線，決定亮度。

environment mapping: 物體周圍擺放圖片，映射在物體上。
shadow mapping: 預先計算物體陰影範圍，貼上陰影圖片。

電腦所能繪製的現象十分稀少。至今仍有許多光學現象，繪製尚未成功，同志仍須努力。

UVa 12313

Sampling

一、反射折射：追蹤光線軌跡，列舉數種可能的方向。

二、發射：增加焦點射向像素的光線數量，射中的顏色們取平均數，產生平滑、模糊、抗鋸齒效果。

anti-alias: 增加亂數數量，取平均數。
motion blur: 根據物體速率，決定亂數偏移量。
depth of field: 根據物體遠近，決定亂數偏移量。

射線數量是一個自訂常數，射線方向的偏移量是一群二維亂數。光線反射折射，採用球形；光線發射，採用正方形。

繪製三角形！

光源：一個點光源。光學：僅反射（入射角等於反射角）、無折射。材質：完美漫射。光線追蹤演算法： Ray Tracing 。無取樣。

圖片很陽春。如果想看更逼真的圖片，可以上網搜尋，或者自己動手畫畫看吧！

mesh rendering — texture

texture

以上介紹了光線照明系統，以下介紹表面紋路系統。

物體表面通常不是均一顏色、不是均一高低。工程師的解決之道：自訂表面紋理。紋理包括了顏色、高度、法向量等類型。

texture generation

製造紋理的方法有：請攝影師拍攝實際照片，請設計師繪製美工圖片，請工程師研發演算法。

製造紋理屬於圖片處理的範疇。原理是運用雜訊，產生紋理的顏色、高度、法向量等等，營造逼真畫面。要是不想自行製作紋理，亦可下載現成的紋理、下載現成的紋理。

texture mapping

將紋理貼上物體表面。物體表面、紋理，建立座標對應關係。請參考這篇文章。

簡易的方式是：物體的每個三角形（四邊形），各使用一片正方形紋理。採用三角形座標（四邊形座標），得到座標對應關係。請參考 image warping ，屬於圖片處理的範疇。

texture mapping: texture coordinates

將紋理布置於物體周圍。重設紋理的座標系統。

正方體：使用六片紋理，作為正方體的六個面。
圓柱體：使用一片紋理，左右銜接。（座標對應：長寬對應高度和角度）
半球體：使用一片紋理，中央凸出。（座標對應：長寬對應經緯）

texture mapping: mesh parameterization

將紋理映射至物體表面。重設物體表面的座標系統。

攤平：物體從某處剪開、攤平，得到對應關係。
　　　周界可以盡量調整成紋理形狀、內界可以盡量調整成整齊網格。
中心：源自物體中心的放射線，擊中表面和紋理，得到對應關係。
光學：源自焦點的射線，經由反射擊中紋理，得到對應關係。

攤平細分為兩種映射方式。

UV mapping：物體表面切割成棋盤方格，橫向座標稱作U，縱向座標稱作V。
UVW mapping：承上，處處追加深度數值。深度座標稱作W。

texture filtering

bilinear filtering：只有一張紋理。採用image warping改變紋理形狀。
trlinear filtering：考慮相機遠近，預先製作各種大小的紋理。scale transform。
anisotropic filtering：考慮相機角度，預先製作各種視角的紋理。shear transform。

二維紋理的映射當中，紋理與表面的大小形狀，經常不相符，必須調整紋理的大小形狀。

改變紋理的大小形狀，紋理可能出現鋸齒、可能失真。仿效內插的觀念，讓紋理柔順平滑。

texture data structure / texture atlas

   mipmap: 紋理預先縮放成各種比率，以應付各種遠近距離的呈現觀感。
heightmap: 附帶高度資訊。

紋理的資料結構。我沒有研究，請參考這篇文章、 Wavefront 的 obj 檔案格式。

texture embossing

重新設定表面法向量、表面高度，令表面凹凸不平、有立體感、有陰影，宛如壓印。請參考這篇文章、這篇文章。

bump mapping: 表面是平面，重新設定每一處的高低。
normal mapping: 表面是平面，重新設定每一處的法向量。
displacement mapping: 三角形頂點沿法向量移動。
parallax mapping: http://exibeo.net/docs/parallax_mapping.pdf
relief mapping: http://graphics.cs.brown.edu/games/SteepParallax/index.html

normal interpolation

重新設定表面法向量，使其圓滑。

想得到三角形上某一點的法向量：

一、求得三角形的正面的法向量。三個頂點叉積，即得。

二、求得三角形的三個頂點的法向量。一個頂點有許多個相鄰的三角形。相鄰三角形的法向量相加之後，當作該頂點的法向量。然而模型本身多半已經提供精準的頂點的法向量，可以省略這兩步驟。

三、求得三角形的任意一點的法向量。想要求得內插比重，直覺的方式是：將一次內插重新表示成線性變換矩陣，然後求反矩陣 ── 然而當三角形與原點共平面，反矩陣就不存在了。推薦的方式是「 barycentric interpolation 」，三塊小三角形的面積，就是內插比重。

法向量們方向漸層改變。打光後，三角形表面彷彿圓滑凸起。

形狀看似改變了，但是實際位置沒變。物體邊緣會產生破綻。

Point Camera::interpolate(Triangle t, Point hit)
{
// 點到三角形頂點的向量
Point v0 = t.vertex[0] - hit;
Point v1 = t.vertex[1] - hit;
Point v2 = t.vertex[2] - hit;
// 以四面體體積比例作為面積比例
float c2 = dot(cross(v0, v1), t.normal);
float c0 = dot(cross(v1, v2), t.normal);
float c1 = dot(cross(v2, v0), t.normal);
float c = c0 + c1 + c2;
// 一次內插。以三角形三個頂點的法向量，得到交點的法向量。
// 由於檔案裡面已經提供頂點法向量，就直接拿來用了。
Point n = (t.vnormal[0] * (c0 / c))
+ (t.vnormal[1] * (c1 / c))
+ (t.vnormal[2] * (c2 / c));
return n;
}

normal encoding

將一個法向量重新表示成一個浮點數，節省儲存空間。請參考這篇文章。

mesh rendering — model to camera

perspective projection

如何計算三維空間的一個點，在圖片上對應的 XY 座標呢？

先以「點積」求得三個方向的投影量、即是真實距離 x y z 。

再以「相似三角形邊長成比例」的原理，藉由 z 和 depth 的比例，求得投影距離 x' y' 。 x z 構成的三角形，縮小為 depth/z 倍，得到 x' ； y z 構成的三角形，縮小為 depth/z 倍，得到 y' 。

注意到，真實距離和投影距離都是以圖片中心為基準，距離可以是負值。最後我們調整投影距離成為圖片座標。

Point Camera::project(Point p)
{
// 運用點積求得真實距離
Point view = p - eye;
Point d = {
dot(view, dirx),
dot(view, diry),
dot(view, dirz)
};
// 相似三角形邊長成比例：
// 縮小為 depth/z 倍，求得投影距離。
if (d.z == 0) return d; // 避免除以0！
d = d / fabs(d.z) * depth;
// 求得圖片座標
return (Point){X/2 + d.x, Y/2 + d.y, d.z};
}

繪製空心三角形！

此處的模型是台大資訊系。

窮舉每個三角形，把三角形三個頂點投射到圖片上，求得圖片座標。運用 OpenGL 畫出每個三角形的外框，最後形成了「線框（ wireframe ）圖」。

void display()
{
glClear(GL_COLOR_BUFFER_BIT);
for (int i=0; i<(int)triangleList.size(); ++i)
{
Triangle& t = triangleList[i];
Point p0 = camera.project(t.vertex[0]);
Point p1 = camera.project(t.vertex[1]);
Point p2 = camera.project(t.vertex[2]);
glColor3f(1., 1., 1.); // 白色
glBegin(GL_LINES);
glVertex2f(p0.x, p0.y); glVertex2f(p1.x, p1.y);
glVertex2f(p1.x, p1.y); glVertex2f(p2.x, p2.y);
glVertex2f(p2.x, p2.y); glVertex2f(p0.x, p0.y);
glEnd();
}
glutSwapBuffers();
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei)w, (GLsizei)h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluOrtho2D(0, w, 0, h);
}
int main(int argc, char **argv)
{
const char fileName[] = "csie.tri";
bool load = LoadFile(fileName);
if (!load) cout << "Cannot open: " << fileName << endl;
camera.init();
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB);
glutInitWindowSize(400, 300);
glutInitWindowPosition(100, 100);
glutCreateWindow("Wireframe");
glClearColor(0., 0., 0., 0.);
glShadeModel(GL_SMOOTH);
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutMainLoop();
return 0;
}

polygon filling

大家應該會畫空心三角形了。現在來畫實心三角形吧！

把三角形三個頂點投射到圖片上，求得圖片座標。套用填充多邊形演算法，把三角形畫到圖片上。

鉤勒線段的部分，採用了「一次內插」，求得準確的三角形邊界；然後運用 ceil 和 floor 函數，讓相鄰三角形的接縫密合。

Triangle* triangle[X][Y];
void FillEdge(Point p1, Point p2)
{
int xmini = max(0, (int)ceil (min(p1.x, p2.x)));
int xmaxi = min(X-1, (int)floor(max(p1.x, p2.x)));
for (int x = xmini; x <= xmaxi; ++x)
{
// 一次內插。用X座標求得Y座標。
float y = (p2.x == p1.x ? p1.y : (p2.y - p1.y) / (p2.x - p1.x) * (x - p1.x) + p1.y);
ymin[x] = min(ymin[x], y);
ymax[x] = max(ymax[x], y);
}
}
void FillTriangle(Triangle& t)
{
// 三角形三個頂點，圖片座標
Point p[3];
for (int i=0; i<3; ++i)
p[i] = camera.project(t.vertex[i]);
// 計算X座標的極小值、極大值
float xmin = +1e9, xmax = -1e9;
for (int i=0; i<3; ++i)
{
xmin = min(xmin, p[i].x);
xmax = max(xmax, p[i].x);
}
// 初始化Y座標的極小值、極大值
int xmini = max(0, (int)ceil (xmin));
int xmaxi = min(X-1, (int)floor(xmax));
for (int x = xmini; x <= xmaxi; ++x)
{
ymin[x] = +1e9;
ymax[x] = -1e9;
}
// 計算Y座標的極小值、極大值
for (int i=0; i<3; ++i)
FillEdge(p[i], p[(i+1)%3]);
// 填充
for (int x = xmini; x <= xmaxi; ++x)
{
int ymini = max(0, (int)ceil (ymin[x]));
int ymaxi = min(Y-1, (int)floor(ymax[x]));
for (int y = ymini; y <= ymaxi; ++y)
triangle[x][y] = &t;
}
}

Triangle* triangle[X][Y];
void FillLine(float x1, float x2, int y, Triangle& t)
{
if (!(y >= 0 && y < Y)) return;
int xmini = max(0, (int)ceil (x1));
int xmaxi = min(X-1, (int)floor(x2));
for (int x = xmini; x <= xmaxi; x++)
triangle[x][y] = &t;
}
void FillTriangle(Triangle& t)
{
// 三角形三個頂點，圖片座標
Point A = camera.project(t.vertex[0]);
Point B = camera.project(t.vertex[1]);
Point C = camera.project(t.vertex[2]);
// 依照y座標排序
if (A.y > B.y) swap(A, B);
if (B.y > C.y) swap(B, C);
if (A.y > B.y) swap(A, B);
// 計算斜率
float dx1 = (B.y-A.y > 0) ? (B.x-A.x)/(B.y-A.y) : 0;
float dx2 = (C.y-A.y > 0) ? (C.x-A.x)/(C.y-A.y) : 0;
float dx3 = (C.y-B.y > 0) ? (C.x-B.x)/(C.y-B.y) : 0;
// 三角形的邊界
float x1 = A.x;
float x2 = A.x;
int y = (int)ceil(A.y); // 導致x1 x2不夠精確，可能漏填
int By = (int)floor(B.y);
int Cy = (int)floor(C.y);
// 填充
if (dx1 > dx2) {
for (; y<=By; y++, x1+=dx2, x2+=dx1)
FillLine(x1, x2, y, t);
x2 = B.x;
for (; y<=Cy; y++, x1+=dx2, x2+=dx3)
FillLine(x1, x2, y, t);
} else {
for (; y<=By; y++, x1+=dx1, x2+=dx2)
FillLine(x1, x2, y, t);
x1 = B.x;
for (; y<=Cy; y++, x1+=dx3, x2+=dx2)
FillLine(x1, x2, y, t);
}
}

visible surface determination

近的三角形，必須擋住遠的三角形。求得三角形與焦點的距離，才能判斷誰近誰遠。

從焦點往圖片像素的射線，射向三角形，以「三角形與直線交點」求得距離。為了避免緩慢的 sqrt 運算，我們不求直線距離，而是求 dirz 方向的距離、也就是深度。

float Camera::zvalue(int x, int y, Triangle t)
{
Point view = (dirx * (x - X/2))
+ (diry * (y - Y/2))
+ (dirz * depth);
float dv = dot(view, t.normal);
float dt = dot(t.vertex[0] - eye, t.normal);
if (dv == 0) return 1e9; // 三角形與視線平行
return dot(view * dt / dv, dirz);
}

最後一行程式碼可以簡化。 * dt / dv 可以提到 dot 外面。 view 是由 dirx 、 diry 、 dirz 組成，這三個向量互相垂直； view 投影到 dirz 上，只需要看 dirz 方向有多少投影量，點積結果顯然是 depth 。

return dt / dv * depth;

depth 是定值。有些人為了加速，甚至不乘上 depth ，只求個縮放倍率。倍率 1.0 剛好位於圖片上。

return dt / dv;

一邊填充三角形，一邊判斷深度。三角形的交接處，可以優先選擇靠近焦點的三角形，或者為了爭取速度而不做判斷。

float zvalue[X][Y]; // z-buffer，初始化為無限大
Triangle* triangle[X][Y]; // 每個像素對應的三角形
void FillTriangle(Triangle& t)
{
......
for (int x = xmini; x <= xmaxi; ++x)
{
int ymini = max(0, (int)ceil (ymin[x]));
int ymaxi = min(Y-1, (int)floor(ymax[x]));
for (int y = ymini; y <= ymaxi; ++y)
{
// 判斷深度，取深度最小者
float z = camera.zvalue(x, y, t);
if (z < zvalue[x][y])
{
zvalue[x][y] = z;
triangle[x][y] = &t;
}
}
}
}

古人曾經使用另一種演算法：運用「 BSP tree 」預先排序所有三角形，依照先後順序繪製，就不必判斷遠近。但是無法處理三角形循環互疊、無法處理相機移動，速度也極慢，現今沒人用。

illumination

此處介紹懶惰的打光方式。

光線與表面垂直，感覺最亮；光線與表面平行，感覺最暗。光線與表面的夾角大小，決定了亮暗。更精準來說，光線的垂直分量大小，決定了亮暗。

光線向量與法向量的點積，即是亮暗程度。設定為單位向量，亮暗程度就是 0.0 到 1.0 之間的數字。至於法向量可以使用上個章節提到的演算法求得。

ambient：物體發光，亮度為定值。
diffuse：光線向量與法向量的點積，作為亮暗程度。
specular：視線向量與反射向量的點積，作為亮暗程度。
          取k次方，夾角越小、亮度驟升。
modified specular：「視線向量與光線向量的中垂線」與法向量的點積，作為亮暗程度。
                   取k次方，夾角越小、亮度驟升。

Lambert model = c1⋅ambient + c2⋅diffuse
Phong model = c1⋅ambient + c2⋅diffuse + c3⋅specular
Blinn-Phong model = c1⋅ambient + c2⋅diffuse + c3⋅modified specular

Point light = {1,0,0}; // 平行光源方向（單位向量）
float Camera::illuminate(Triangle t, Point hit,
Point view, Point light)
{
view = normalize(view);
light = normalize(light);
// 交點的法向量
Point weight = interpolate(t, hit);
Point normal = (t.vnormal[0] * weight.x)
+ (t.vnormal[1] * weight.y)
+ (t.vnormal[2] * weight.z);
// 反射向量
Point reflect = normalize(normal * (dot(light, normal) * -2.0) + light);
// 視線向量與光線向量的中垂線
Point bisector = normalize(view + light);
// 全域基本亮度（0.0 ~ 1.0）
float ambient = 1.0;
// 垂直分量亮度（0.0 ~ 1.0）
float diffuse = fabs(dot(light, normal));
// 亮者越亮，產生亮點（0.0 ~ 1.0）
float specular = pow(fabs(dot(view, reflect)), 5.0);
// 亮者越亮，產生亮點（0.0 ~ 1.0）
float specular2 = pow(fabs(dot(normal, bisector)), 20.0);
// 光源照射的、焦點看到的，如果是不同面，就無亮度。
// （缺陷：即將翻面的三角形整片漏失）
if (dot(view, t.normal) * dot(light, t.normal) <= 0)
diffuse = specular = specular2 = 0;
// 光源照射的、焦點看到的，如果是不同面，就無亮度。
// （缺陷：即將翻面的三角形邊緣滲光）
// if (dot(view, normal) * dot(light, normal) <= 0)
// diffuse = specular = specular2 = 0;
// 自行調配比重，揉合三種亮度。
return (ambient * 0.2)
+ (diffuse * 0.4)
+ (specular * 0.4);
}
Point Camera::interpolate(Triangle t, Point p)
{
Point v0 = t.vertex[0] - p;
Point v1 = t.vertex[1] - p;
Point v2 = t.vertex[2] - p;
float c2 = dot(cross(v0, v1), t.normal);
float c0 = dot(cross(v1, v2), t.normal);
float c1 = dot(cross(v2, v0), t.normal);
float c = c0 + c1 + c2;
return (Point){c0, c1, c2} / c;
}

shading

素描的 shading ，著重線條樣式；電腦繪圖的 shading ，著重填充方式。

flat shading：求三角形任一點的顏色（例如重心），其餘通通一樣。
Gouraud shading：求三角形三頂點的顏色，其餘一次內插。
Phong shading: 求三角形每一點的顏色，法向量內插。

// Phong shading
Point Camera::color(int x, int y, Triangle t, float zvalue)
{
// 從焦點往圖片像素的射線。
Point v = (dirx * (x - X/2)) + (diry * (y - Y/2)) + (dirz * depth);
// 取得三角形顏色。判斷焦點面對三角形的正面還是背面。
Point c = (dot(v, t.normal) < 0) ? t.foreColor : t.backColor;
// 顏色×亮暗程度=呈現顏色
return c * illuminate(t, eye + (v * zvalue), v);
}

繪製實心三角形！

void display()
{
glClear(GL_COLOR_BUFFER_BIT);
// 初始化z-buffer
for (int x = 0; x < X; ++x)
for (int y = 0; y < Y; ++y)
zvalue[x][y] = +1e9;
// 填充每個三角形
for (int i=0; i<(int)triangleList.size(); ++i)
FillTriangle(triangleList[i]);
// 畫出所有像素
for (int x = 0; x < X; ++x)
for (int y = 0; y < Y; ++y)
{
if (zvalue[x][y] == +1e9) continue;
Point c = camera.color(x, y, *triangle[x][y], zvalue[x][y]);
glColor3f(c.x, c.y, c.z);
glBegin(GL_POINTS);
glVertex2f(x, y);
glEnd();
}
glutSwapBuffers();
}

culling

backface culling：預先剔除物體背後的三角形。
occlusion culling：預先剔除被其他物體遮住的三角形。
visibility culling：預先剔除視野範圍（field of view）之外的三角形。

culling 有三種，這裡只介紹 backface culling 。

如果物體有著密封外殼，背向焦點的三角形一定被遮住；如果物體有著破洞外殼、物體是一張薄紙，背向焦點的三角形才有機會露臉。

如果物體有著密封外殼，我們可以剔除背向焦點的三角形，避免無謂的填充，加快程式速度。

bool Camera::toward(Triangle t)
{
return dot(t.vertex[0] - eye, t.normal) < 0;
}
void display()
{
......
for (int i=0; i<(int)triangleList.size(); ++i)
if (camera.toward(triangleList[i]))
FillTriangle(triangleList[i]);
......
}

UVa 12628

clipping

裁切有兩種。第一種是設定視野範圍（ field of view ）。

我們可以設定左、右、上、下、遠、近邊界，設定六個平面作為邊界、裁切物體。值得一提的是，以近平面裁切物體，讓我們可以瞧見物體內部（此時就不應該實施 backface culling 了）。我們習慣讓近平面等於圖片位置。

當然也可以設定不規則形狀的邊界。

void FillEdge(Point p1, Point p2)
{
// 左邊界和右邊界。太左、太右就不畫。
int xmini = max(20, (int)ceil (min(p1.x, p2.x)));
int xmaxi = min(80, (int)floor(max(p1.x, p2.x)));
......
}
void FillTriangle(Triangle& t)
{
......
// 左邊界和右邊界。太左、太右就不畫。
int xmini = max(20, (int)ceil (xmin));
int xmaxi = min(80, (int)floor(xmax));
for (int x = xmini; x <= xmaxi; ++x)
{
ymin[x] = +1e9;
ymax[x] = -1e9;
}
......
for (int x = xmini; x <= xmaxi; ++x)
{
// 下邊界和上邊界。太低、太高就不畫。
int ymini = max(30, (int)ceil (ymin[x]));
int ymaxi = min(70, (int)floor(ymax[x]));
for (int y = ymini; y <= ymaxi; ++y)
{
float z = camera.zvalue(x, y, t);
// 近邊界和遠邊界。太近、太遠就不畫。
// if (z < camera.depth) continue;
if (z < 1.0) continue;
if (z > 5.0) continue;
if (z < zvalue[x][y])
{
zvalue[x][y] = z;
triangle[x][y] = &t;
}
}
}
}

裁切有兩種。第二種是阻止三角形伸展至焦點背後。

三角形頂點位於焦點背後，投射到圖片上就會歪斜！先前我們倒退一萬步，巧妙避開這個議題；現在我們想瞧瞧物體內部、讓圖片與焦點靠近物體、裁切物體，就必須解決這個議題。

解決方式是：運用「多邊形裁切」，以近平面裁切三角形，去除太近的部分，之後才投射、填充。裁切之後剩下的多邊形，通常會再剖分成三角形，方便套用原本的投射、填充程式碼。

省略

第一種裁切，對象是圖片像素；第二種裁切，對象是三角形。

3D transformation

物體平移、縮放、旋轉；相機平移、縮放、旋轉。一共六種。

物體旋轉。物體自轉，換個觀點來看，就是相機繞物體公轉。與其搬動大量三角形，不如只搬動一個相機。旋轉 dirx 、 diry 、 dirz 三個向量，重新倒退一萬步，就完成物體旋轉。

struct Matrix {float a[3][3];};
// 矩陣乘矩陣
Matrix operator*(Matrix m1, Matrix m2)
{
Matrix m = {{{0,0,0},{0,0,0},{0,0,0}}};
for (int i=0; i<3; ++i)
for (int j=0; j<3; ++j)
for (int k=0; k<3; ++k)
m.a[i][j] += m1.a[i][k] * m2.a[k][j];
return m;
}
// 矩陣乘向量
Point operator*(Matrix m, Point p)
{
return (Point){
m.a[0][0] * p.x + m.a[0][1] * p.y + m.a[0][2] * p.z,
m.a[1][0] * p.x + m.a[1][1] * p.y + m.a[1][2] * p.z,
m.a[2][0] * p.x + m.a[2][1] * p.y + m.a[2][2] * p.z
};
}

Point angle;
void Camera::init()
{
radius = 1000; depth = 300;
center = mesh_center();
angle = (Point){0,0,0}; // 一開始沒有旋轉
rotate();
}
void Camera::rotate()
{
// 製作三維旋轉矩陣
float c, s;
c = cos(angle.x); s = sin(angle.x);
Matrix rx = {{{1,0,0},{0,c,s},{0,-s,c}}};
c = cos(angle.y); s = sin(angle.y);
Matrix ry = {{{c,0,-s},{0,1,0},{s,0,c}}};
c = cos(angle.z); s = sin(angle.z);
Matrix rz = {{{c,s,0},{-s,c,0},{0,0,1}}};
// 實施旋轉
Matrix r = rx * ry * rz;
dirx = r * (Point){1,0,0};
diry = r * (Point){0,0,1};
dirz = r * (Point){0,1,0};
light = r * (Point){1,0,0}; // 光源跟著轉
// 倒退一萬步
eye = center - (dirz * radius);
}

相機旋轉。相機自轉，換個觀點來看，就是物體繞相機公轉。其實不必想太多，直接旋轉相機就好了。

物體旋轉通常用於 3D 繪圖軟體，相機旋轉通常用於第一人稱射擊遊戲，焦點旋轉則不常使用。由於 clipping 的關係，焦點旋轉時會看不見近身景色。第一人稱射擊遊戲的角色是站在相機中心、採用相機旋轉，而不是站在焦點、採用焦點旋轉。

省略

物體縮放。以物體中心為原點，縮放三角形頂點座標。

相機縮放。以相機焦點為原點，縮放三角形頂點投射之後的圖片座標。

物體縮放是先縮放再投影，相機縮放是先投影再縮放，兩者的視覺效果並不相同。物體縮放有鏡頭拉近拉遠的效果，相機縮放則是整張畫面等比例放大縮小。

省略

物體平移、相機平移。懶的講了，兩者視覺效果相同。

繪製動感三角形！

// 用鍵盤的w與s控制遠近
void keyboard(unsigned char key, int x, int y)
{
if (key == 'w') camera.radius -= 50;
else if (key == 's') camera.radius += 50;
camera.rotate(); // 記得更新焦點位置
glutPostRedisplay();
}
// 用滑鼠旋轉物體
int press_x, press_y;
Point press_angle;
void mouse(int button, int state, int x, int y)
{
if (state == GLUT_DOWN)
{
press_x = x; press_y = y;
press_angle = camera.angle;
}
}
// 用滑鼠旋轉物體
void motion(int x, int y)
{
camera.angle = press_angle + (Point){y - press_y, 0, x - press_x} / 40;
camera.rotate(); // 記得更新焦點位置
glutPostRedisplay();
}
int main(int argc, char **argv)
{
const char fileName[] = "csie.tri";
bool load = LoadFile(fileName);
if (!load) cout << "Cannot open: " << fileName << endl;
camera.init();
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB);
glutInitWindowSize(400, 300);
glutInitWindowPosition(100, 100);
glutCreateWindow("Computer Graphics");
glClearColor(0., 0., 0., 0.);
glShadeModel(GL_SMOOTH);
// 每當需要重新繪圖，自動呼叫display函式。
glutDisplayFunc(display);
// 每當改變視窗大小，自動呼叫reshape函式。
glutReshapeFunc(reshape);
// 每當按下鍵盤按鍵，自動呼叫keyboard函式。
glutKeyboardFunc(keyboard);
// 每當按下滑鼠按鍵，自動呼叫mouse函式。
glutMouseFunc(mouse);
// 每當移動滑鼠游標，自動呼叫motion函式。
glutMotionFunc(motion);
// 開始繪圖
glutMainLoop();
return 0;
}

voxel rendering

voxel rendering （ volume rendering ）

voxel

「像素 pixel 」和「體素 voxel 」兩者概念相仿，二維與三維的差別而已。

像素數值，通常代表 RGB 顏色；體素數值，通常代表物質密度。物質密度越高，體素數值越高。

替現實生活的物體建立體素，是一套複雜的學問。所幸網路上已經有電腦斷層掃描的資料。此處使用的 CTHead 是 8bit TIFF 圖片檔案，圖片一張張疊起來，像素成了體素。

這份資料中，皮肉密度低、體素數值低，骨骼密度高、體素數值高。我不清楚物質密度與體素數值是否恰好成正比。

const int N = 99;
const int VX = 256;
const int VY = 256;
const int VZ = N * 2 - 1;
short img[VZ][VY][VX];
void LoadFile()
{
// 運用OpenCV依序讀取99張圖片。
for (int z=0; z<N; ++z)
{
char name[50];
sprintf(name, "cthead-8bit\\cthead-8bit%03d.tif", z+1);
cv::Mat image = cv::imread(name);
for (int x=0; x<VX; ++x)
for (int y=0; y<VY; ++y)
{
cv::Vec3b intensity = image.at<cv::Vec3b>(y, x);
img[z*2][y][x] = (intensity.val[0] + intensity.val[1] + intensity.val[2]) / 3;
}
}
// 所有相鄰圖片之間，一次內插一張圖片，
// 讓頭殼看起來不會太扁。
for (int z=0; z<N-1; ++z)
for (int x=0; x<VX; ++x)
for (int y=0; y<VY; ++y)
img[z*2+1][y][x] = (img[z*2][y][x] + img[z*2+2][y][x]) / 2;
}

normal vector

以「梯度 gradient 」的單位向量，當作法向量。梯度的計算過程很簡單：右邊減左邊、遠處減近處、上面減下面，除以兩個間距，分別得到 XYZ 三個方向的變化程度。

bool involume(int x, int y, int z)
{
return x >= 0 && x < VX
&& y >= 0 && y < VY
&& z >= 0 && z < VZ;
}
Point gradient(int x, int y, int z)
{
if (involume(x+1, y+1, z+1) &&
involume(x-1, y-1, z-1))
// 稍後會計算單位向量，此處不必除以2。
return (Point){
img[z][y][x+1] - img[z][y][x-1],
img[z][y+1][x] - img[z][y-1][x],
img[z+1][y][x] - img[z-1][y][x]
};
else
return (Point){0, 0, 0};
}

ray marching （ ray casting ）

體素視作固體 solid 、液體 liquid 、氣體 gas ，有著不同的光線追蹤演算法。此處先介紹固體的演算法：

一、找到射線從容積的哪裡射入、哪裡射出。

二、套用鉤勒直線演算法，求得射線碰到的體素們。

三、設定臨界值，求得射線無法穿越的那個體素，即為所求。

void Camera::hitvolume(Point view, float& zmin, float& zmax)
{
// 容積的六個面（各面只取一個頂點）
static Point vertex[6] =
{
{0,0,0},{0,0,0},{0,0,0},
{VX,0,0},{0,VY,0},{0,0,VZ}
};
// 容積的六個面的法向量
static Point normal[6] =
{
{1,0,0},{0,1,0},{0,0,1},
{1,0,0},{0,1,0},{0,0,1}
};
// 求得射線打中容積的哪一個表面、求得z-value。
zmin = +1e9, zmax = -1e9;
for (int i=0; i<6; ++i)
{
// ray-plane intersection
float dv = dot(view, normal[i]);
float dt = dot(vertex[i] - eye, normal[i]);
if (dv == 0) continue;
float z = dt / dv;
if (!(z > 1.0 && z < +1e9)) continue;
// 由於浮點數誤差，
// 我們只能用複雜的方式，判斷射線是否打中表面。
Point hit = eye + (view * z);
// if (involume(hit.x, hit.y, hit.z))
if (( (hit.x >= 0 && hit.x < VX)
|| (normal[i].x == 1.0) ) &&
( (hit.y >= 0 && hit.y < VY)
|| (normal[i].y == 1.0) ) &&
( (hit.z >= 0 && hit.z < VZ)
|| (normal[i].z == 1.0) ))
{
// 如果射線打中表面，就更新z-value。
if (z < zmin) zmin = z;
if (z > zmax) zmax = z;
}
}
}

Point Camera::color(int x, int y)
{
// 焦點往圖片像素的射線
Point view = (dirx * (x - X/2))
+ (diry * (y - Y/2))
+ (dirz * depth);
Point normalizeview = normalize(view);
// 求得射線打中容積的哪一個表面、求得z-value。
float zmin = +1e9, zmax = -1e9;
hitvolume(view, zmin, zmax);
if (zmin == +1e9 || zmax == -1e9)
return (Point){0,0,0};
// DDA algorithm，求得射線碰到的體素們。
Point pmin = eye + (view * zmin);
// Point pmax = eye + (view * zmax);
// Point length = pmax - pmin;
Point length = view * (zmax - zmin);
int step = ceil(max(
fabs(length.x),
fabs(length.y),
fabs(length.z)
));
Point gap = length / step;
for (int i=0; i<step; ++i)
{
pmin = pmin + gap;
int x = round(pmin.x);
int y = round(pmin.y);
int z = round(pmin.z);
if (!involume(x, y, z)) continue;
// 體素小於60，射線就持續穿越體素。
if (img[z][y][x] < 60) continue;
// 體素大於等於60，即為所求。馬上著色。
Point normal = normalize(gradient(x,y,z));
float s = illuminate(normal, normalizeview);
return (Point){1,1,1} * s;
}
// 射線穿透整個容積，無色。
return (Point){0,0,0};
}

設定不同的臨界值，就得到不同器官。皮肉密度低、骨骼密度高，因此臨界值低就得到皮肉，臨界值高就穿越皮肉、得到骨骼。

最困難的地方，就是如何讓電腦自動找到臨界值、讓電腦自動畫出最顯眼的圖片。這屬於影像辨識、人工智慧的領域，讀者可以自行尋找相關資料。

一種臨界值，得到一種器官。採用半透明顏色，就可以同時畫出很多器官。

ray marching （ ray casting ）

此處介紹液體、氣體的演算法：

一、體素一共有 256 種數值（以此模型為例，其他模型不見得皆如此），替每一種數值設定顏色、暨透明程度。

二甲、由遠往近讀取體素，揉合顏色：遠方顏色與當前顏色，依照比例（當前顏色的透明程度）揉合，遞推下去。

二乙、亦得由近往遠讀取體素：透明程度增加一個次方，乘上當前顏色，累加下去。

void InitColor()
{
// 初始化顏色
for (int i=0; i<255; ++i)
color_func[i] = (Point){0,0,0};
// 皮肉顏色
for (int i=60; i<85; ++i)
color_func[i] = (Point){1,0.7,0};
// 骨骼顏色
for (int i=100; i<130; ++i)
color_func[i] = (Point){1,1,1};
// 初始化為完全透明
for (int i=0; i<255; ++i)
alpha_func[i] = 0;
// 皮肉不透明程度（皮肉顏色密度）
for (int i=60; i<85; ++i)
alpha_func[i] = 0.2;
// 骨骼不透明程度（骨骼顏色密度）
for (int i=100; i<130; ++i)
alpha_func[i] = 0.9;
}

Point Camera::color(int x, int y)
{
......
Point color = {0,0,0};
for (int i=0; i<step; ++i)
{
// 由遠往近讀取體素
pmax = pmax - gap;
int x = round(pmax.x);
int y = round(pmax.y);
int z = round(pmax.z);
if (!involume(x, y, z)) continue;
// 著色
Point normal = normalize(gradient(x,y,z));
float s = illuminate(normal, normalizeview);
Point c = color_func[img[z][y][x]] * s;
// 揉合顏色
float a = alpha_func[img[z][y][x]];
color = color * (1.0 - a) + c * a;
}
return color;
}

設定不同的顏色暨透明程度，得到不同的視覺感受。

ray marching: sparse voxel octree

若想加速，將所有體素存入「 octree 」資料結構，依照區域分類所有體素。適用於體素數量稀少、遠少於容積大小的情況。