region資料結構: 索引儲存
uniform grid
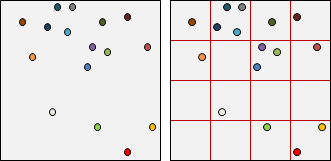
嗯,就是方格紙。將整個世界劃分為等寬方格。
實作方式是一個二維陣列,對應方格紙。陣列每一格是一個串列,對應每個方格包含的物體。
如果物體跨據多個方格,那麼同時儲存於多個方格。
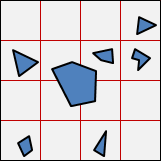
插入、刪除、搜尋的時間複雜度是O(N),N為物體數量。然而,串列長度通常遠少於N,這種時間複雜度標記法缺乏意義。
region
區域資料結構
儲存大量幾何物體、查詢周遭幾何物體的資料結構。
物體位置不限,到處遍布,甚至重疊。物體形狀不限,點、直線、曲線、矩形、圓形、三角形、……。物體形狀不需一致。
這樣的資料結構,目前沒有正式學術名稱。有人稱作space partitioning data structure。也有人稱作spatial data structure。至於region這個名稱是我自己定的。
區域資料結構的功能:
一、找到相交物體。例如輸入一條線段/射線/直線,輸出碰觸的物體們。
簡易方式是枚舉法。窮舉每個物體,一一判斷相交。
進階方式是區域資料結構。事先劃分區域,依照區域儲存物體。只需要檢查直線穿越的區域、區域裡面的物體,不需要檢查所有區域、所有物體。
二、找到相鄰物體。例如輸入一條線段/射線/直線,輸出距離範圍之內的物體們。
事先調整區域大小,盡量符合距離範圍。只需要檢查附近的區域們,不需要檢查更遠的區域們。
位置是區域的特例
當輸入一律是點,當物體一律是多邊形(化作一群頂點),那麼可以使用point資料結構的長方形範圍查詢。
region資料結構: 索引儲存
uniform grid

嗯,就是方格紙。將整個世界劃分為等寬方格。
實作方式是一個二維陣列,對應方格紙。陣列每一格是一個串列,對應每個方格包含的物體。
如果物體跨據多個方格,那麼同時儲存於多個方格。

插入、刪除、搜尋的時間複雜度是O(N),N為物體數量。然而,串列長度通常遠少於N,這種時間複雜度標記法缺乏意義。
region資料結構: 循序儲存
sparse array【尚無正式名稱】
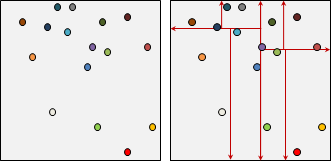
陣列元素是物體暨uniform grid索引值。物體依照uniform grid索引值排序。
為了快速檢查相鄰物體,將uniform grid所有方格重新編號,讓相鄰方格擁有相近編號,稱作space-filling curve。物體依照編號排序。一個物體往前往後檢查足夠數量的物體,就能涵蓋相鄰物體。
常見的編號順序是Hilbert curve。整體走勢呈U型。最差的情況下,位於中央直線左側的方格,抵達右方相鄰方格,需要經過逾半數方格。當每個方格都有物體,需要檢查逾半數物體,
另一種編號順序是z-order curve。最差的情況下,檢查較少物體。缺點是不保證相鄰編號是相鄰方格。
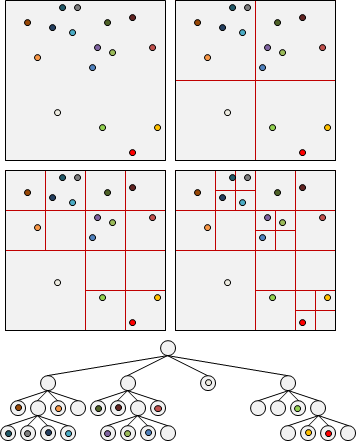
region資料結構: quadtree
bitree / quadtree / octree
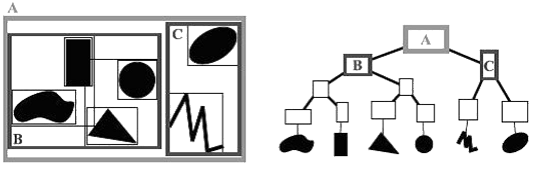
二元樹、四元樹、八元樹分別是一、二、三維的版本。
以四元樹為例:分割平面為四等分,視情況可以遞迴分割下去,越分越細。物體放在樹葉。
插入、刪除、搜尋的時間複雜度是O(N),N為物體數量。然而,樹的高度通常遠少於N,這種時間複雜度標記法缺乏意義。確切的時間複雜度難以估計,取決於樹深與分枝數。
UVa 297 806 11941 11948
region資料結構: bounding volume hierarchy