polygon

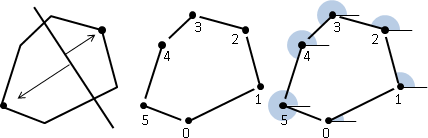
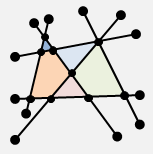
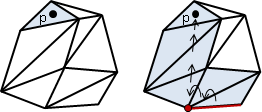
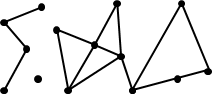
「多邊形」。許多條邊，端點對著端點，串接成一圈的圖形。

資料結構

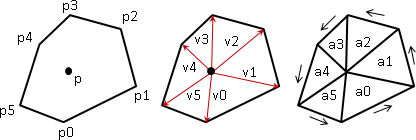
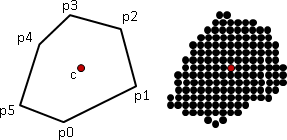
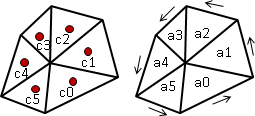
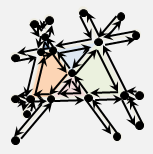
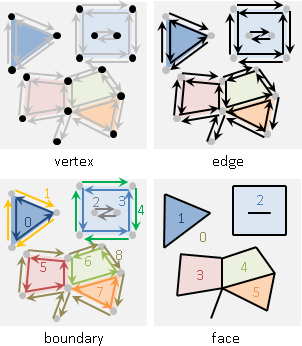
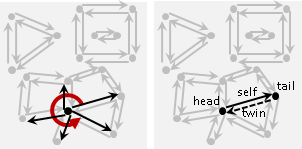
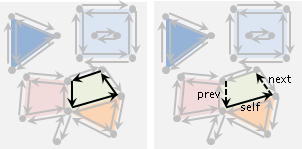
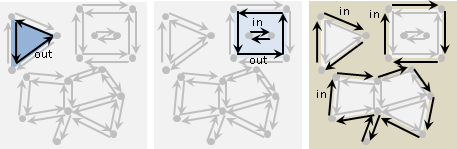
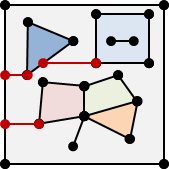
想要記錄一個多邊形的資訊，有許多種方法，例如：一、按照連接順序把多邊形的邊放到一個陣列裡面；二、按照連接順序把多邊形的頂點放到一個陣列裡面；三、挑一個頂點作為起點，從起點開始按照連接順序把各條邊的長度、邊與邊之間的夾角放到一個陣列裡面。

這幾種方法的空間複雜度都是O(N)，N為多邊形的頂點數目，也可以說是邊的數目。

struct Point {float x, y;}; struct Segment {Point p1, p2;}; struct Walk {float length, angle;}; Segment polygon[10]; // 一 Point polygon[10]; // 二 Point original; // 三 Walk polygon[10];

多邊形分類：數學的觀點

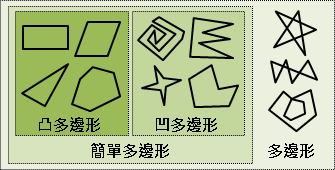
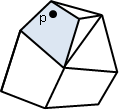
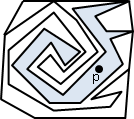
多邊形（polygon）：許多條邊，端點對著端點，串接成一圈的圖形。
簡單多邊形（simple polygon）：所有的邊都不相交，只有相鄰的邊可以相交於一個頂點。
凹多邊形（convave polygon）：多邊形內部必有兩點連線，穿過多邊形外部。
凸多邊形（convex polygon）：多邊形內部所有兩點連線，都在多邊形內部。

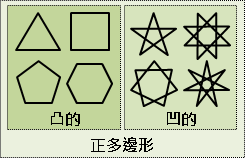
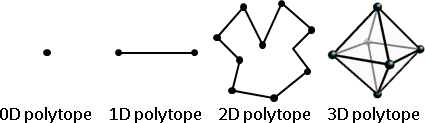
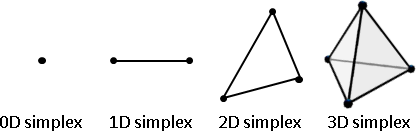
正多邊形（regular polygon）：每條邊都一樣長、每個角都一樣大的多邊形。
凸的正多邊形：就是我們熟悉的正三角形、正方形、正五邊形、……。
凹的正多邊形：就是正五角星、正七角星、正八角星、……。
　　　　　　　詳細資料請自行搜尋關鍵字regular star polygon。

UVa 12300

多邊形分類：計算學的觀點

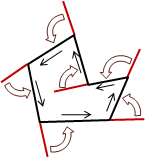
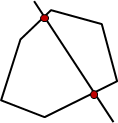
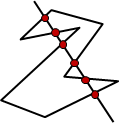
簡單多邊形（simple polygon）。所有的邊都不相交，只有相鄰的邊可以相交於一個頂點。

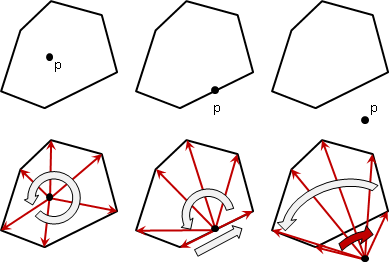
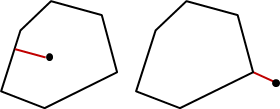
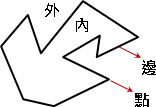
簡單多邊形圍出一個明確的封閉區域。一般的多邊形無法分辨內外，而簡單多邊形可以明確分辨內外。

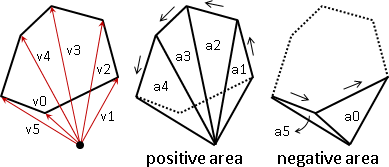
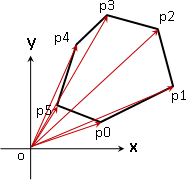
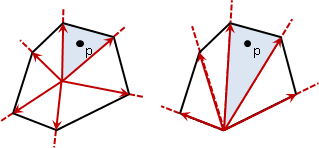
沿邊走一回，剛好自旋360°；所有外角相加是360°。我們習慣讓頂點順序是逆時針方向，以符合叉積的方向。

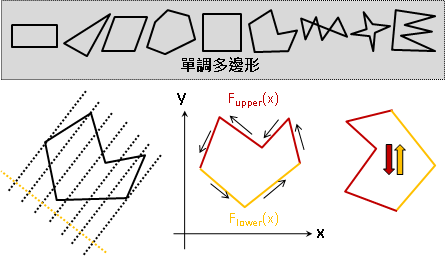
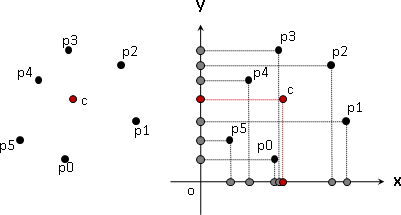
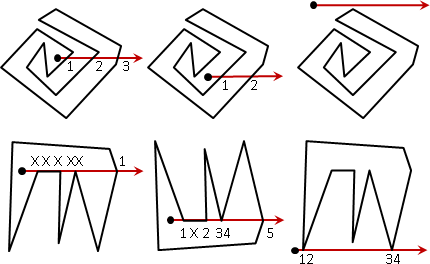
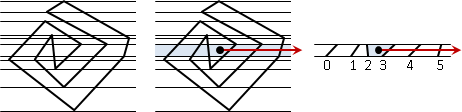
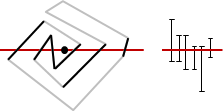
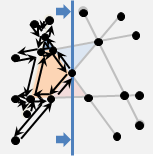
單調多邊形（monotone polygon）。至少存在一條直線，這條直線的每一條垂直線，與單調多邊形的交點在兩點以下。

換句話說，單調多邊形旋轉至某個角度之後，可以切割成上下兩條鏈，兩條鏈都符合函數定義。單調多邊形可以寫成兩個函數。

換句話說，單調多邊形有兩條鏈，在某個方向上先單調遞增、再單調遞減，彷彿單峰函數。

簡單一句話：單調多邊形是兩條已排序的鏈。

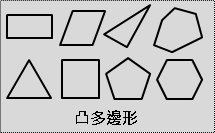
凸多邊形（convex polygon）。總是朝同一個方向轉彎。

凸多邊形同時是簡單多邊形和單調多邊形，無論哪種方向都是單調多邊形。數學性質非常強！

正交多邊形（orthogonal polygon、rectilinear polygon、axis-parallel polygon、axis-aligned polygon）。每條邊都平行於座標軸，轉彎總是轉90°或270°。

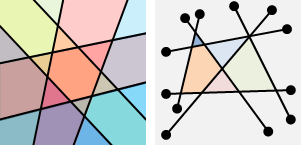
有洞多邊形（polygon with hole）。多邊形的內部有數個洞，洞的內部有數個多邊形。有洞多邊形，其實不屬於多邊形，其實是數個多邊形。我們可以用順時針代表多邊形、逆時針代表洞。多邊形的聯集、交集、差集，結果常常是有洞多邊形。

多邊形面積（surveyor's formula）

凸多邊形是特例中的特例，我們試著從凸多邊形開始觀察。

運用分治法的思想，把凸多邊形分割成三角形，就容易計算面積了。取凸多邊形內部一點作為基準點，連線至各個頂點，把凸多邊形切開成許多個三角形。現在我們可以利用叉積，計算每個三角形的面積；然後通通加起來，得到凸多邊形面積。

詳細的步驟是：
一、建立基準點往各個頂點的向量。
二、依照頂點順序，計算相鄰向量的叉積，得到平行四邊形面積。
三、除以二，得到三角形面積。
四、三角形面積通通加起來，得到凸多邊形面積。

步驟三和步驟四可以顛倒，除以二的次數變成只有一次：
三、平行四邊形面積通通加起來，得到凸多邊形面積的兩倍。
四、除以二，得到凸多邊形面積。

事實上，基準點也可以在凸多邊形邊界、甚至是外部。此時叉積的結果有正值和負值，正值恰好對應到總面積，負值剛好對應到多餘面積。通通加起來，正負相消之後，恰好仍是凸多邊形面積。

基準點設定在原點是最方便的，如此一來就不必特地計算基準點往各個頂點的向量，可以直接拿相鄰兩點的座標計算叉積。

此演算法可以推廣到簡單多邊形，甚至是一般的多邊形。時間複雜度O(N)，N為多邊形的頂點數目。

我們可以把結果寫成數學式子，正是知名的行列式公式：

        1  | x1   x2   x3     xN-1   xN   x1 |
area = --- |    ×    ×    ...      ×    ×    |
        2  | y1   y2   y3     yN-1   yN   y1 |

右下斜線相乘取正號，左下斜線相乘取負號，然後通通加起來，除以二。
如果是逆時針旋轉，求出來為正值。
如果是順時針旋轉，求出來為負值，必須再取絕對值。

一般來說我們會讓多邊形頂點順序為逆時針順序，以求得正值。

struct Point {float x, y;} p[10 + 1]; // 十個頂點的多邊形 float cross(Point a, Point b) { return a.x * b.y - b.x * a.y; } void polygon_area() { p[10] = p[0]; float area = 0.0; for (int i=0; i<10; ++i) area += cross(p[i], p[i+1]); cout << "多邊形面積為" << fabs(area) / 2.0; } struct Point {float x, y;} p[10]; // 十個頂點的多邊形 void polygon_area() { float area = 0.0; for (int i=0; i<10; ++i) { area += p[i].x * p[(i+1)%10].y; area -= p[i].y * p[(i+1)%10].x; } cout << "多邊形面積為" << fabs(area) / 2.0; } struct Point {float x, y;} p[10]; // 十個頂點的多邊形 void polygon_area() { // 避免了%運算、避免了重複的+1運算，執行時間較短。 float area = 0.0; for (int i=10-1, j=0; j<10; i=j++) { area += p[i].x * p[j].y; area -= p[i].y * p[j].x; } cout << "多邊形面積為" << fabs(area) / 2.0; }

UVa 10060 10652 922

多面體體積

與多邊形面積的原理相同。基本單元從三角形變成了四面體。

struct Point {float x, y, z;}; struct Facet {Point a, b, c;} f[10]; float dot(Point a, Point b) { return a.x * b.x + a.y * b.y + a.z * b.z; } Point cross(Point a, Point b) { return (Point){ a.y * b.z - b.y * a.z, a.z * b.x - b.z * a.x, a.x * b.y - b.x * a.y }; } float triple(Point a, Point b, Point c) { return dot(a, cross(b, c)); } void polyhedron_volume() { float volume = 0.0; for (int i=0; i<10; i++) volume += triple(f[i].a, f[i].b, f[i].c); cout << "多面體體積為" << fabs(volume) / 6.0; }

多邊形形心 / 多邊形重心

重力場均勻的時候，重心退化成為形心。

一群點的重心，是這些點的座標平均數，也就是X座標的平均數、Y座標的平均數。

多邊形的重心，則是多邊形內部暨邊界上所有點的座標平均數。但是不見得是所有頂點的座標平均數。

只有一些特別的多邊形，重心恰好是所有頂點的座標平均數──例如三角形的重心，恰好是三個頂點的座標平均數。

使用分治法的概念，把多邊形切開成許多個三角形，分別計算各個三角形的重心。然後以三角形面積作為權重，計算三角形重心的加權平均數，就得到多邊形的重心。

      o + p0 + p1          o + p1 + p2  
c0 = —————————————   c1 = —————————————   ...
           3       ,            3       ,

      cross(p0, p1)          cross(p1, p2)
a0 = ———————————————   a1 = ———————————————   ...
           2         ,            2         ,

            c0 ⋅ a0 + ... + c9 ⋅ a9
centroid = —————————————————————————
                 a0 + ... + a9

struct Point {int x, y;} p[10]; void polygon_centroid() { float cx = 0, cy = 0, w = 0; for (int i=10-1, j=0; j<10; i=j++) { float a = cross(p[i], p[j]); cx += (p[i].x + p[j].x) * a; cy += (p[i].y + p[j].y) * a; w += a; } cout << "多邊形的重心座標為"; cout << '(' << cx/3/w << ',' << cy/3/w << ')'; }

UVa 10002 132 ICPC 4838

判斷一個點是否在凸多邊形內部

很直覺但是不精準的方式，是沿著凸多邊形外圍繞一圈，看看點是否在每一條邊的同側。若發現叉積皆小於零，即表示點在多邊形內部：若發現叉積等於零，即表示點在凸多邊形上、或在凸多邊形某條邊的延長線上；若發現叉積大於零，則表示點在凸多邊形外部。

正確的方式，是將點到凸多邊形頂點的各條向量，利用叉積運算判斷是否都往同一方向旋轉，如果都是往同一方向旋轉，則表示點在凸多邊形內部；如果中途出現反方向旋轉，則表示點在凸多邊形外部；如果中途出現叉積為零的情況，表示點在凸多邊形上，而且就在對應的邊上。

時間複雜度O(N)，N為凸多邊形的頂點數目。

UVa 109 361 476 477 478 10078 10291 10321

不斷查詢一個點是否在凸多邊形內部

凸多邊形內任選一點作為基準點（例如最低最左頂點）。凸多邊形的所有頂點，按照角度排序。以二元搜尋找出給定點在哪個夾角之內，以外積判斷給定點是否在此夾角構成的三角形裡面。

O(NlogN)預處理，O(logN)求答案。

http://morris821028.github.io/2014/08/28/oj/uva/uva-12048/

UVa 12048

判斷一個點是否在簡單多邊形內部

從給定點開始，往隨便一個方向射出一條射線（例如水平往右射線），看看穿過多少條邊。如果穿過偶數次，表示點在簡單多邊形外部；如果穿過奇數次，表示點在簡單多邊形內部。

要小心處理的情況：射線穿過頂點、射線與邊重疊。

時間複雜度O(N)，N為簡單多邊形的頂點數目。

struct Point {float x, y;} p[10]; float interpolate_x(float y, Point p1, Point p2) { if (p1.y == p2.y) return p1.x; return p1.x + (p2.x - p1.x) * (y - p1.y) / (p2.y - p1.y); } // 沒有判斷點在多邊形上的情況 bool point_in_polygon(Point t) { bool c = false; for (int i = 10-1, j = 0; j < 10; i = j++) if ((p[i].y > t.y) != (p[j].y > t.y) && t.x < interpolate_x(t.y, p[i], p[j])) c = !c; return c; }

UVa 634 11030 10348

不斷查詢一個點是否在簡單多邊形內部

梯形剖分。掃描線由下往上移動，每當遇到頂點，就切割一塊垂直區間。針對一塊垂直區間，掃描線由左往右移動，每當遇到邊，就切割一塊水平區間。

首先二元搜尋垂直區間，然後二元搜尋水平區間，就能知道水平往右射線穿過多少條邊。

O(N²)預處理，O(logN)求答案。

多邊形拆成邊，樹套樹。第一層線段樹，依照Y區間儲存邊；第二層二元搜尋樹，依照X座標排序邊。涵蓋射線起點的線段樹節點們，各自查詢二元搜尋樹，就能知道水平往右射線穿過多少條邊。

O(Nlog²N)預處理，O(log²N)求答案。

二元搜尋樹改成串列。涵蓋射線起點的線段樹節點們，各自窮舉串列，就能知道水平往右射線穿過多少條邊。

O(NlogN)預處理，O(logN + K)求答案。

http://morris821028.github.io/2019/02/16/zj-e021/

判斷直線是否與凸多邊形相交

窮舉凸多邊形每一條邊，判斷相交。時間複雜度O(N)。

不斷查詢直線是否與凸多邊形相交

在直線的垂線方向上，尋找凸多邊形的兩個極點，然後判斷是否在直線兩側。

凸多邊形的所有頂點暨下一條邊，按照角度排序。角度範圍是0°到360°，形成嚴格遞增數列。直線的垂線化成兩個角度（相差180°），分別二元搜尋，得到兩個極點。實作時，不必計算實際角度，改用點積與叉積來比較角度大小。

O(NlogN)預處理，O(logN)求答案。

ICPC 4837

判斷直線是否與簡單多邊形相交

窮舉簡單多邊形每一條邊，判斷相交。時間複雜度O(N)。

不斷查詢直線是否與簡單多邊形相交

多邊形拆成線段。線段存入資料結構uniform grid、quadtree、kd-tree、BVH、R-tree，以便快速查詢相交。

O(N²)預處理，O(N)求答案，實務上遠少於N²和N。

點與凸多邊形的距離

窮舉凸多邊形每一條邊，計算距離。時間複雜度O(N)。

我們無法使用二元搜尋。點與凸多邊形各點的距離們，點與凸多邊形各邊的距離們，沒有遞增遞減性質。

不斷查詢點與凸多邊形的距離

目前沒有快速的演算法。只能使用枚舉法。

網路上可以找到一個錯誤的演算法，只能求出點與凸多邊形各點的最短距離：

一、凸多邊形頂點，建立Voronoi diagram，以便快速查詢最近頂點。二、Voronoi diagram，建立point location資料結構，以便快速查詢所屬區域。

O(NlogN)預處理，O(logN)求答案。

arrangement

大量線條，形成大量區域，稱作「布置」。

線條可以是直線、線段、曲線。

UVa 754 1708

planar straight line graph

尋找交點，截斷線條，以便建立點與邊。

形成「平面直線圖」：點不重疊、邊不相交、邊呈直線。

名稱源自圖論的「平面圖」：點不重疊、邊不相交。

half-edge

緊接著，一條無向邊改成兩條有向邊，以便建立界與面。

這種有向邊，俗稱「半邊」。

資料結構

布置包含四種元件：點、邊、界、面。

兩點得一邊，多邊得一界，多界得一面。

四種元件習慣拆開處理，各自採用適合的資料結構。

資料結構：點

大量資料的資料結構「array」。

點：座標們

const int V = 100; struct Point {float x, y;} vertex[V]; // array void build_vertex() { // 點：座標們 for (int i=0; i<V; ++i) { float x, y; cin >> x >> y; vertex[i] = (Point){x,y}; } }

資料結構：邊

圖的資料結構「adjacency lists」。

點：出邊們（依照角度排序）
邊：反向邊、起點、終點

const int E = 300 * 2; int edge[E][2]; // edge list vector<int> adj[V]; // adjacency lists void build_edge() { // 點：出邊們（依照角度排序） for (int j=0; j<E; j+=2) { // 無向邊 int a, b; cin >> a >> b; // 一條無向邊改成兩條有向邊 // 正向邊：無向邊編號乘2加0 // 反向邊：無向邊編號乘2加1 edge[j+0][0] = a; // 正向邊 edge[j+0][1] = b; edge[j+1][0] = b; // 反向邊 edge[j+1][1] = a; adj[a].push_back(j+0); // 正向邊 adj[b].push_back(j+1); // 反向邊 } // 各點的出邊，依照角度排序。 for (int i=0; i<V; i++) sort(adj[i].begin(), adj[i].end(), cmp_angle); } // 邊：反向邊、起點、終點 int twin(int i) {return i^1;} int head(int i) {return edge[i][0];} int tail(int i) {return edge[i][1];} // 角度排序 bool cmp_angle(const int& i, const int& j) { Point o = vertex[ head(i) ]; Point p1 = vertex[ tail(i) ] - o; Point p2 = vertex[ tail(j) ] - o; if (p1.y == 0 && p2.y == 0 && p1.x * p2.x <= 0) return p1.x > p2.x; if (p1.y == 0 && p1.x >= 0 && p2.y != 0) return true; if (p2.y == 0 && p2.x >= 0 && p1.y != 0) return false; if (p1.y * p2.y < 0) return p1.y > p2.y; float c = cross(p1, p2); return c > 0 || (c == 0 && fabs(p1.x) < fabs(p2.x)); }

資料結構：界

多邊形的資料結構「array」。

界：擁有的邊（外界逆時針、內界順時針）
邊：所屬的界、上一條邊、下一條邊

一個界擁有多條邊，通通串連在一起。兩種方式：

一、主角是點，窮舉轉角。

二、主角是邊，繞行邊界。

// 邊：上一條邊、下一條邊 int prev_edge[E]; int next_edge[E]; // 主角是點，窮舉轉角。 void build_edge_for_boundary() { for (int i=0; i<V; ++i) { int n = adj[i].size(); for (int j=n-1, k=0; k<n; j=k++) { // 轉角 k-1 -> i -> k int curr = adj[i][j]; int prev = twin(adj[i][k]); prev_edge[curr] = prev; next_edge[prev] = curr; } } } // 界：擁有的邊（外界逆時針、內界順時針） vector<vector<int>> boundary; // 邊：所屬的界 int boundary_of_edge[E]; void build_boundary() { int* visit = boundary_of_edge; // 改個名字 for (int j=0; j<E; ++j) visit[j] = -1; int B = 0; for (int j=0; j<E; ++j) { if (visit[j] == -1) continue; visit[j] = B; vector<int> polygon; polygon.push_back(j); // 儲存有向邊編號 for (int x=next_edge[j]; x!=j; x=next_edge[x]) { visit[x] = B; polygon.push_back(x); } boundary.push_back(move(polygon)); B++; } } // 每條邊在adj之中的索引值 int adj_k[E]; // 主角是邊，繞行邊界。 void build_edge_for_boundary() { for (int i=0; i<V; i++) for (int k=0; k<(int)adj[i].size(); ++k) adj_k[ adj[i][k] ] = k; } // 界：擁有的邊（外界逆時針、內界順時針） vector<vector<int>> boundary; // 邊：所屬的界 int boundary_of_edge[E]; void build_boundary() { int* visit = boundary_of_edge; // 改個名字 for (int j=0; j<E; ++j) visit[i] = -1; int B = 0; for (int j=0; j<E; j++) { if (visit[j] == -1) continue; visit[j] = B; vector<int> polygon; polygon.push_back(j); // 儲存有向邊編號 for (int curr=j, next=-1; next!=j; curr=next) { int i = tail(curr); int k = adj_k[twin(curr)]; k--; if (k < 0) k = adj[i].size() - 1; next = adj[i][k]; visit[next] = B; polygon.push_back(next); } boundary.push_back(move(polygon)); B++; } }

資料結構：面

互斥集的資料結構「disjoint-sets forest」。

面：擁有的界

一個面擁有多個界，通通聯集在一起。三種方式：

一、射線法：每個外界的極點（例如最左點），往外切一刀（例如水平往左射線），找到第一個擊中的界，屬於同一面。

二、平移的掃描線：原理同上。從左往右掃描，維護一棵線段樹，以便快速找到第一個擊中的界。因為最左點已排序，所以disjoint-sets forest總是添加樹葉。disjoint-sets forest簡化成disjoint-set array，聯集的時間複雜度簡化成O(1)。

三、設定一個極大的正方形邊界，有洞多邊形切開為簡單多邊形：原理同上。一個面只有一個界。雖然界與面數量翻倍，但是實際上只多了幾條邊，而且也不需要disjoint-sets forest了。

【待補程式碼】

// disjoint-sets forest struct DisjointSets { int p[E]; void init(int n) {for (int i = 0; i <= n; i++) p[i] = i;} int find(int x) {return p[x] == x ? x : p[x] = find(p[x]);} void merge(int x, int y) {p[find(y)] = find(x);} }; // 面：擁有的界 DisjointSets face; void build_face() { int B = boundary.size(); face.init(B); for (int i=0; i<B; i++) { // 略過內界 if (area(boundary[i]) > 0) continue; // 最左點（編號） int l = leftmost(boundary[i]); // 最左點的水平往左射線，找到第一個射中的界。 int j = raycast(boundary, vertex[l]); // 聯集界，成為面。 if (j != -1) face.merge(i, j); } } float area(vector<int> polygon[]) { float sum = 0; for (int i=0; i<polygon.size(); i++) { int e = polygon[i]; int v1 = edge[e][0]; int v2 = edge[e][1]; sum += cross(vertex[v1], vertex[v2]); } return sum / 2; } int leftmost(vector<int> polygon) { int e = polygon[i][0]; int v = edge[e][0]; int l = v; for (int j=1; j<polygon.size(); j++) { int e = polygon[i][j]; int v = edge[e][0]; if (vertex[v].x < vertex[l].x) l = v; } return l; } int raycast(vector<vector<int>> polygons, Point p) { // 我不會實作 }

資料結構：點邊界面（doubly connected edge list）

DCEL是四種元件的資料結構的豪華總匯。

DCEL原本只包含點與邊，但是實務上又追加了界與面。

一、每個點紀錄所有出邊。以便取得鄰點。
二、每個點排序所有出邊。平面圖才有的特性。
三、每條邊紀錄所屬面。以便取得鄰面。
四、每條邊紀錄反向邊。以便取得另一個鄰面。
五、每個界紀錄所有邊。以便判斷內外。
六、每個面記錄所有界。以便判斷區域。

點：座標、出邊們（逆時針順序）
邊：反向邊、起點、終點、所屬的界、上一條邊、下一條邊、所屬的面
界：起始邊（外界逆時針、內界順時針）、下一個界
面：外界（只有一個）、內界們

struct half_edge; struct vertex { float x, y; // 座標 struct half_edge* list; // 出邊們（依照角度排序） }; struct boundary { struct half_edge* head; // 起始邊（外界逆時針、內界順時針） struct boundary* next; // 下一個界 }; struct face { struct boundary* out; // 外界（只有一個） struct boundary* in; // 內界們 }; struct half_edge { struct half_edge* twin; // 反向邊 struct half_edge* prev; // 上一條邊 struct half_edge* next; // 下一條邊 struct vertex* head; // 起點 struct vertex* tail; // 終點 struct boundary* bound; // 所屬的界 struct face* face; // 所屬的面 };

求得布置

掃描線。「segment intersection」略作修改。時間複雜度O((N+K)logN)，N是線段端點數量，K是交點數量。

不斷查詢一個點在哪個區域，區域是三角剖分。

散步法：任選一個三角形、其一條邊、其一個點，作為起點，朝向目標前進，穿越相鄰三角形。

O(N)預處理，O(K)求答案。K是交點數量。

Kirkpatrick's algorithm：重新三角剖分。我沒有學會。

O(N)預處理，O(logN)求答案。

不斷查詢一個點在哪個區域，區域是凸分割。

我沒有研究。

不斷查詢一個點在哪個區域，區域是簡單多邊形。

解法如同「不斷查詢一個點是否在簡單多邊形內部」。

所有多邊形拆成線段。從給定點開始，往隨便一個方向射出一條射線（例如水平往右射線），找出最先擊中的簡單多邊形。

O(NlogN)預處理，O(logN + K)求答案。

UVa 1075 ICPC 4125

不斷查詢一個點在哪個區域，區域是有洞多邊形。

有洞多邊形改成簡單多邊形，所有多邊形拆成線段。

O(NlogN + NK)預處理，O(logN + K)求答案。

http://morris821028.github.io/2018/07/08/uva-12310/

UVa 12310

polyhedron

「多面體」。許多個面，邊緣對著邊緣，包覆成一圈的圖形。

三種元件：點、邊、面。

點的資料結構

約定俗成是陣列：每個格子儲存點座標，三個浮點數XYZ。

const int V = 100; struct Vertex {float x, y, z;} vertex[V];

查詢點編號、查詢最近點：額外使用區域資料結構，諸如uniform grid、quadtree，請見本站文件「region」。

面的資料結構

約定俗成是陣列：每個格子儲存多邊形頂點的編號。

const int F = 100; struct Face {vector<int> v;} face[F];

查詢面編號、查詢最近面：額外使用區域資料結構，諸如BVH、R-tree，請見本站文件「region」。

排序所有面：額外使用位置排序資料結構BSP tree，請見本站文件「position」。

邊的資料結構

約定俗成是DCEL：每個點紀錄所有鄰邊（鄰點編號）、每個點排序所有鄰邊（逆時針順序）、每條邊紀錄反向邊、每條邊紀錄所屬面。請見本站文件「arrangement」。

struct Edge { int v; // 鄰點編號 int f; // 面編號 Edge* twin; // 反向邊 }; vector<Edge> adj[V];

查詢邊編號：查詢面編號之後，檢查所有鄰邊。

polytope

「多胞形」。多邊形推廣到任意維度。

點、線段、多邊形、多面體，分別是零一二三維的多胞體。

simplex

「單體」、「單形」。每個維度的最基礎的多胞形。

點、線段、三角形、四面體，分別是零一二三維的單體。

simplicial complex

「單體複形」、「複形」。一大堆單體。可以相互銜接，銜接之處也是單體。