curve

「曲線」。形狀隨意的線。

parametric curve

想要建立曲線，可以使用函數。

這種方式有個嚴重的問題：曲線是一個函數，每個X值只對應一個Y值；曲線不能到處亂繞，只能左右伸展。

要解決這個問題，最簡單的方法，就是分別處理X軸與Y軸。用一個函數專門處理X座標，用另一個函數專門處理Y座標。

{ x(t) = abs(t-2) exp(abs(t-1))
{ y(t) = abs(4t)

代入t = -0.1，得到一個座標(x(-0.1), y(-0.1)) = (4.673, 0.4)
代入t =    0，得到一個座標(x(0)   , y(0)   ) = (5.436, 0)
代入t =  0.1，得到一個座標(x(0.1) , y(0.1) ) = (6.308, 0.4)

這個手法叫做「參數式parametric equation」，t就是參數。高中數學、微積分課程都有提到，不是什麼艱深晦澀的玩意。

二維曲線，使用兩個函數。三維曲線，使用三個函數。

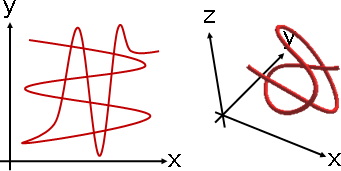
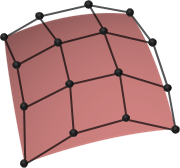
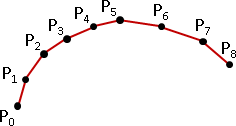
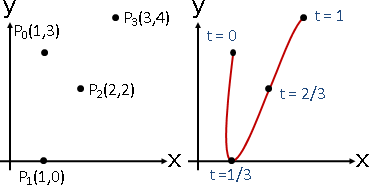polynomial curve

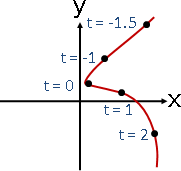
想要建立曲線，可以使用多項式函數，平滑柔順。

{ x(t) = 1 + 2t¹ + 3t² - t³
{ y(t) = 2 - t¹ + t² - t³

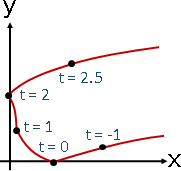
代入t = -0.1，得到一個座標(x(-0.1), y(-0.1)) = (0.831, 2.111)
代入t =    0，得到一個座標(x(0)   , y(0)   ) = (1, 2)
代入t =  0.1，得到一個座標(x(0.1) , y(0.1) ) = (1.229, 1.909)

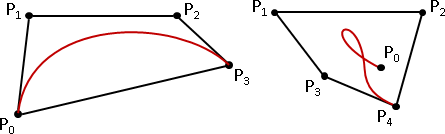
引入control point以操控曲線

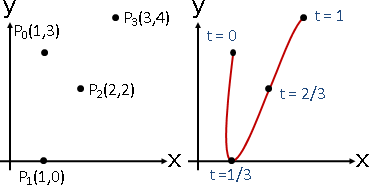
想要操控曲線，最便捷的方式，就是點上幾個點，然後運用「多項式內插」，得到一條穿過這些點的曲線。操控點的位置，就操控了曲線的位置。

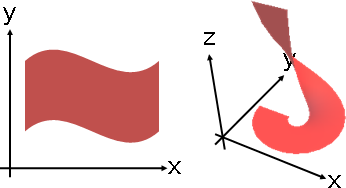
電腦擅於處理大量資料。我們可以製作非常多條曲線，讓曲線銜接曲線，就得到各式各樣的形狀了。因此，通常我們不會製作無限長的曲線，其實製作一小段曲線就夠了。

我們習慣讓t值的範圍是0到1。設定三個點、用二次多項式實施內插，三個點的t值分別是0、0.5、1。或者設定四個點、用三次多項式實施內插，四個點的t值分別是0、1/3、2/3、1。

一次多項式只能產生直線，二次以上的多項式才能產生曲線。

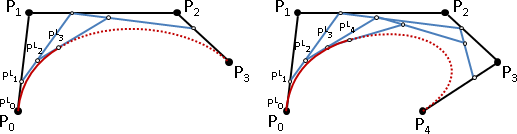
引入knot point以微調曲線

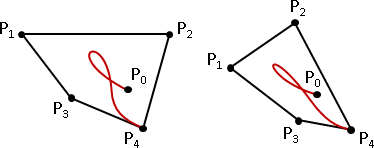
自由調整控制點的參數t，不一定要等分。曲線仍然穿過所有控制點，但是曲線形狀會改變。

額外建立一條數線，範圍是t = 0到t = 1。在數線上放置四個樞紐點，分別調控四個控制點的參數t。第一個樞紐點固定於t = 0，最後一個樞紐點固定於t = 1。

簡單起見，以下暫不考慮樞紐點。

小結

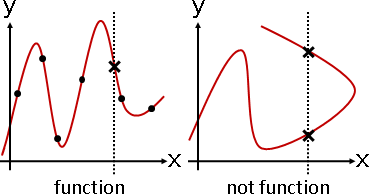
一、欲建立二維平面的曲線，X座標、Y座標分開處理，採用兩個函數。
二、欲使曲線平滑，採用多項式函數。
三、欲穿過四個點，採用三次多項式函數。
四、代入0≤t≤1，畫出一條曲線。
五、挪動四個控制點，畫出各種曲線。

採用Vandermonde matrix演算法，進行多項式內插。

一、設定內插多項式。

平面上四個點
(x₀,y₀) (x₁,y₁) (x₂,y₂) (x₃,y₃)

X座標、Y座標分別處理，採用三次（四項）多項式。
x(t) = a₀t⁰ + a₁t¹ + a₂t² + a₃t³
y(t) = b₀t⁰ + b₁t¹ + b₂t² + b₃t³

二、求得內插多項式的係數。

首先處理X座標！
令四個點對應的t值是 t = 0, 1/3, 2/3, 1
也就是說 x(0) = x₀ , x(1/3) = x₁ , x(2/3) = x₂ , x(1) = x₃

[     0⁰     0¹     0²     0³ ] [ a₀ ]   [ x₀ ]
[ (1/3)⁰ (1/3)¹ (1/3)² (1/3)³ ] [ a₁ ] = [ x₁ ]
[ (2/3)⁰ (2/3)¹ (2/3)² (2/3)³ ] [ a₂ ]   [ x₂ ]
[     1⁰     1¹     1²     1³ ] [ a₃ ]   [ x₃ ]
                                       -1
[ a₀ ]   [     0⁰     0¹     0²     0³ ] [ x₀ ]
[ a₁ ] = [ (1/3)⁰ (1/3)¹ (1/3)² (1/3)³ ] [ x₁ ]
[ a₂ ]   [ (2/3)⁰ (2/3)¹ (2/3)² (2/3)³ ] [ x₂ ]
[ a₃ ]   [     1⁰     1¹     1²     1³ ] [ x₃ ]

[ a₀ ]   [    1     0     0     0 ] [ x₀ ]
[ a₁ ] = [ -5.5     9  -4.5     1 ] [ x₁ ]
[ a₂ ]   [    9 -22.5    18  -4.5 ] [ x₂ ]
[ a₃ ]   [ -4.5  13.5 -13.5   4.5 ] [ x₃ ]

a₀ =    1 x₀ +     0 x₁ +     0 x₂ +    0 x₃
a₁ = -5.5 x₀ +     9 x₁ +  -4.5 x₂ +    1 x₃
a₂ =    9 x₀ + -22.5 x₁ +    18 x₂ + -4.5 x₃
a₃ = -4.5 x₀ +  13.5 x₁ + -13.5 x₂ +  4.5 x₃

三、曲線X座標公式。

無論一開始給定哪四個點，矩陣都是固定不變的。
無論一開始給定哪四個點，往後都可以直接套用公式，求得多項式係數。
a₀ =    1 x₀ +     0 x₁ +     0 x₂ +    0 x₃
a₁ = -5.5 x₀ +     9 x₁ +  -4.5 x₂ +    1 x₃
a₂ =    9 x₀ + -22.5 x₁ +    18 x₂ + -4.5 x₃
a₃ = -4.5 x₀ +  13.5 x₁ + -13.5 x₂ +  4.5 x₃

代入到內插多項式
x(t) = a₀t⁰ + a₁t¹ + a₂t² + a₃t³

得到曲線X座標公式
x(t) =  -4.5       (t-1/3) (t-2/3) (t-1) x₀
     +  13.5 (t-0)         (t-2/3) (t-1) x₁
     + -13.5 (t-0) (t-1/3)         (t-1) x₂
     +   4.5 (t-0) (t-1/3) (t-2/3)       x₃

代入各種t值（範圍是0≤t≤1），得到曲線上每個點的X座標。

四、曲線Y座標公式。如法炮製。

x(t) =  -4.5       (t-1/3) (t-2/3) (t-1) x₀
     +  13.5 (t-0)         (t-2/3) (t-1) x₁
     + -13.5 (t-0) (t-1/3)         (t-1) x₂
     +   4.5 (t-0) (t-1/3) (t-2/3)       x₃

y(t) =  -4.5       (t-1/3) (t-2/3) (t-1) y₀
     +  13.5 (t-0)         (t-2/3) (t-1) y₁
     + -13.5 (t-0) (t-1/3)         (t-1) y₂
     +   4.5 (t-0) (t-1/3) (t-2/3)       y₃

五、代入各種t，得到曲線座標。

struct Point {float x, y;}; Point p0 = {1,3}, p1 = {1,0}, p2 = {2,2}, p3 = {3,4}; void curve() { for (float t = 0.0; t <= 1.0; t += 0.01) { float x = -4.5*(t-1/3)*(t-2/3)*(t-1) * p0.x + 13.5*t*(t-2/3)*(t-1) * p1.x + -13.5*t*(t-1/3)*(t-1) * p2.x + 4.5*t*(t-1/3)*(t-2/3) * p3.x; float y = -4.5*(t-1/3)*(t-2/3)*(t-1) * p0.y + 13.5*t*(t-2/3)*(t-1) * p1.y + -13.5*t*(t-1/3)*(t-1) * p2.y + 4.5*t*(t-1/3)*(t-2/3) * p3.y; cout << '(' << x << ',' << y << ')'; } }

basis function

曲線座標公式可以改寫成：參數t的多項式函數的加權平均。

援引線性代數：參數t的多項式函數，視作基底。

x(t) = a₀t⁰ + a₁t¹ + a₂t² + a₃t³

                       [ a₀ ]
     = [ t⁰ t¹ t² t³ ] [ a₁ ]   點積
                       [ a₂ ]
                       [ a₃ ]

                       [    1     0     0     0 ] [ x₀ ]
     = [ t⁰ t¹ t² t³ ] [ -5.5     9  -4.5     1 ] [ x₁ ]
                       [    9 -22.5    18  -4.5 ] [ x₂ ]
                       [ -4.5  13.5 -13.5   4.5 ] [ x₃ ]

                                   [ x₀ ]
     = [ a₀(t) a₁(t) a₂(t) a₃(t) ] [ x₁ ]   前面兩個矩陣先相乘
                                   [ x₂ ]
                                   [ x₃ ]

     = a₀(t)x₀ + a₁(t)x₁ + a₂(t)x₂ + a₃(t)x₃   控制點的座標，視作權重
                                               a₀(t) ... a₃(t)，視作基底
其中
a₀(t) =  -4.5       (t-1/3) (t-2/3) (t-1)
a₁(t) =  13.5 (t-0)         (t-2/3) (t-1)
a₂(t) = -13.5 (t-0) (t-1/3)         (t-1)
a₃(t) =   4.5 (t-0) (t-1/3) (t-2/3)

採用Lagrange interpolation演算法，進行多項式內插。

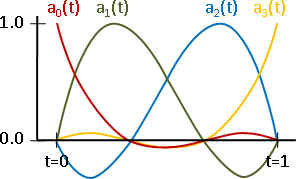
不必算得要死不活，輕鬆得到曲線座標公式：四個多項式函數a₀(t) a₁(t) a₂(t) a₃(t)的加權平均數，權重是四個控制點的座標。

x(t) = a₀(t) x₀ + a₁(t) x₁ + a₂(t) x₂ + a₃(t) x₃

a₀(t) =  -4.5       (t-1/3) (t-2/3) (t-1)
a₁(t) =  13.5 (t-0)         (t-2/3) (t-1)
a₂(t) = -13.5 (t-0) (t-1/3)         (t-1)
a₃(t) =   4.5 (t-0) (t-1/3) (t-2/3)

Hermite curve

改用兩個點暨兩斜率來建立曲線。特色是：曲線與曲線之間，得共用端點、共用斜率，平順銜接，讓銜接點一次可微。

平面上兩個點
(x₀,y₀) (x₁,y₁)

以及這兩個點的斜率
(x₀′,y₀′) (x₁′,y₁′)

三次多項式（四項）作為內插多項式
x (t) = a₀t⁰ +  a₁t¹ +  a₂t² + a₃t³
y (t) = b₀t⁰ +  b₁t¹ +  b₂t² + b₃t³
x′(t) = a₁t⁰ + 2a₂t¹ + 3a₃t²
y′(t) = b₁t⁰ + 2b₂t¹ + 3b₃t²

首先處理X座標！
令兩個點對應的t值分別是 t = 0, 1
也就是說 x(0) = x₀ , x(1) = x₁ , x′(0) = x₀′ , x′(1) = x₁′

x (0) = x₀ = a₀0⁰ +  a₁0¹ +  a₂0² + a₃0³
x (1) = x₁ = a₀1⁰ +  a₁1¹ +  a₂1² + a₃1³
x′(0) = x₀′ = a₁0⁰ + 2a₂0¹ + 3a₃0²
x′(1) = x₁′ = a₁1⁰ + 2a₂1¹ + 3a₃1²

[  1  0  0  0 ] [ a₀ ]   [ x₀  ]
[  1  1  1  1 ] [ a₁ ] = [ x₁  ]
[  0  1  0  0 ] [ a₂ ]   [ x₀′ ]
[  0  1  2  3 ] [ a₃ ]   [ x₁′ ]

[ a₀ ]   [  1  0  0  0 ] [ x₀  ]
[ a₁ ] = [  0  0  1  0 ] [ x₁  ]
[ a₂ ]   [ -3  3 -2 -1 ] [ x₀′ ]
[ a₃ ]   [  2 -2  1  1 ] [ x₁′ ]

a₀ = x₀
a₁ = x₀′
a₂ = -3x₀ + 3x₁ - 2x₀′ - x₁′
a₃ = 2x₀ - 2x₁ + x₀′ + x₁′

x(t) = (2t³ - 3t² + 1) ⋅ x₀
     + (t³ - 2t² + t) ⋅ x₀′
     + (-2t³ + 3t²) ⋅ x₁
     + (t³ - t²) ⋅ x₁′

struct Point {float x, y;}; Point p0 = {1,3}, p1 = {3,4}; Point m0 = {0,9}, m1 = {-3,-6}; void hermite_curve() { for (float t = 0.0; t <= 1.0; t += 0.01) { float x = (2*t*t*t - 3*t*t + 1) * p0.x + (t*t*t - 2*t*t + t) * m0.x + (-2*t*t*t + 3*t*t) * p1.x + (t*t*t - t*t) * m1.x; float y = (2*t*t*t - 3*t*t + 1) * p0.y + (t*t*t - 2*t*t + t) * m0.y + (-2*t*t*t + 3*t*t) * p1.y + (t*t*t - t*t) * m1.y; cout << '(' << x << ',' << y << ')'; } }

Bézier curve四個點的版本

使用四個點，推導出兩個點暨兩斜率。特色是：在使用者介面當中，控制點的位置，比起控制斜率大小來得直覺多了。

平面上四個點
(x₀,y₀) (x₁,y₁) (x₂,y₂) (x₃,y₃)

(x₀,y₀) (x₃,y₃) 是曲線穿過的點，對應的t值分別是 t = 0 , 1
(x₁,y₁) (x₂,y₂) 用來計算斜率，對應的t值分別是 t = 1/3 , 2/3
[(x₁,y₁) - (x₀,y₀)] ÷ 1/3 , [(x₃,y₃) - (x₂,y₂)] ÷ 1/3 是這兩個點的斜率。

[ a₀ ]   [  1  0  0  0 ] [ x₀ ]
[ a₁ ] = [ -3  3  0  0 ] [ x₁ ]
[ a₂ ]   [  3 -6  3  0 ] [ x₂ ]
[ a₃ ]   [ -1  3 -3  1 ] [ x₃ ]

x(t) = (-t³ + 3t² - 3t + 1) ⋅ x₀
     + (3t³ - 6t² + 3t) ⋅ x₁
     + (-3t³ + 3t²) ⋅ x₂
     + (t³) ⋅ x₃

struct Point {float x, y;}; Point p0 = {1,3}, p1 = {1,0}; Point p2 = {2,2}, p3 = {3,4}; void bézier_curve() { for (float t = 0.0; t <= 1.0; t += 0.01) { float x = (-t*t*t + 3*t*t - 3*t + 1) * p0.x + (3*t*t*t - 6*t*t + 3*t) * p1.x + (-3*t*t*t + 3*t*t) * p2.x + (t*t*t) * p3.x; float y = (-t*t*t + 3*t*t - 3*t + 1) * p0.y + (3*t*t*t - 6*t*t + 3*t) * p1.y + (-3*t*t*t + 3*t*t) * p2.y + (t*t*t) * p3.y; cout << '(' << x << ',' << y << ')'; } }

Bézier Curve

仔細觀察基底函數a₀(t) a₁(t) a₂(t) a₃(t)，恰是((1-t) + (t))³的二項式展開，稱作「Bernstein Polynomials」。

藉此推廣成N個控制點：((1-t) + (t))ᴺ⁻¹的二項式展開。

x(t) = (-t³ + 3t² - 3t + 1) ⋅ x₀
     + (3t³ - 6t² + 3t) ⋅ x₁
     + (-3t³ + 3t²) ⋅ x₂
     + (t³) ⋅ x₃

x(t) = 1(1-t)³(t)⁰ ⋅ x₀
     + 3(1-t)²(t)¹ ⋅ x₁
     + 3(1-t)¹(t)² ⋅ x₂
     + 1(1-t)⁰(t)³ ⋅ x₃

x(t) = a₀(t) x₀ + a₁(t) x₁ + a₂(t) x₂ + a₃(t) x₃

a₀(t) = 1(1-t)³(t)⁰
a₁(t) = 3(1-t)²(t)¹
a₂(t) = 3(1-t)¹(t)²
a₃(t) = 1(1-t)⁰(t)³

數學公式（De Casteljau formula）

((1-t) + (t))³的二項式展開，可以化作金字塔遞推。

[layer 0]   x₀     x₁     x₂     x₃
             \    / \    / \    /
[layer 1]      x₀     x₁     x₂
                \    / \    /
[layer 2]         x₀     x₁
               1-t \    / t
[layer 3]            x₀

[layer 0]   x₀⁽⁰⁾ = x₀
            x₁⁽⁰⁾ = x₁
            x₂⁽⁰⁾ = x₂
            x₃⁽⁰⁾ = x₃

[layer 1]   x₀⁽¹⁾ = (1-t) x₀⁽⁰⁾ + t x₁⁽⁰⁾
            x₁⁽¹⁾ = (1-t) x₁⁽⁰⁾ + t x₂⁽⁰⁾
            x₂⁽¹⁾ = (1-t) x₂⁽⁰⁾ + t x₃⁽⁰⁾

[layer 2]   x₀⁽²⁾ = (1-t) x₀⁽¹⁾ + t x₁⁽¹⁾
            x₁⁽²⁾ = (1-t) x₁⁽¹⁾ + t x₂⁽¹⁾

[layer 3]   x₀⁽³⁾ = (1-t) x₀⁽²⁾ + t x₁⁽²⁾

演算法（De Casteljau's algorithm）

相鄰的兩個控制點求加權平均數，遞推下去。

每條線段在t:(1-t)的地方取點，依序連線；遞推下去，得到一點。窮舉0≤t≤1，連成一條曲線。

Bézier curve數學性質

平滑：平滑程度（多項式最高次方），等於控制點的數目減一。

凸包：曲線永遠在控制點的「凸包」內部。

碎形：從切點切開，兩段曲線都是Bézier Curve。左曲線的控制點，即是每一層的最左線段的中繼點。右曲線亦然。

仿射：控制點實施仿射變換（線性變換與平移）求新曲線，即是原曲線實施仿射變換。

Bézier curve進階主題

《A Primer on Bézier Curves 》

《Computer Aided Geometric Design》

arc length：曲線長度。（三個點的特殊公式解）
intersection：兩曲線交點。
degree elevation：新增控制點、樞紐點，而且不改變曲線。
subdivision：曲線一分為二。
reparameterization：調整移動速度。
parameter finding：已知曲線上一點，求得參數。
inverse problem (interpolation)：只知曲線上四個點，求得四個控制點。
rendering：曲線畫在圖片上、填入到像素裡。

此處僅列出一小部分主題。大部分主題都沒有簡易解法。

Bézier curve實際應用

四個點的版本應用廣泛。例如Microsoft PowerPoint的曲線：

例如字體設計：

B-spline curve

一、基底函數a₀(t) a₁(t) a₂(t) a₃(t)，從Bernstein polynomial改成B-spline，得以調整平滑程度。

關於B-spline，請見文站文件「B-spline interpolation」。

二、B-spline自帶樞紐點t₀ t₁ t₂ t₃ ...，得以微調曲線形狀。

Bernstein polynomial屬於B-spline的特例：樞紐點等距。

數學公式（Cox–de Boor formula）

金字塔遞推，最後得到基底函數B-spline。

自訂層數k，B-spline的平滑程度（多項式最高次方）為k。

[layer 0]   a₀(t)  a₁(t)  a₂(t)  a₃(t) a₃₊₁(t) a₃₊₂(t)  ... a₃₊ₖ(t)
               \    / \    / \    / \    / \    / \          /
[layer 1]      a₀(t)  a₁(t)  a₂(t)  a₃(t) a₃₊₁(t)  ... a₃₊ₖ₋₁(t)
                  \    / \    / \    / \    / \          /
    :                                 :
                     \    / \    / \    / \    / \    /
[layer k-1]          a₀(t)  a₁(t)  a₂(t)  a₃(t)  a₄(t)
                        \    / \    / \    / \    /
[layer k]               a₀(t)  a₁(t)  a₂(t)  a₃(t)

[layer 0]
a₀(t)⁽⁰⁾ = (t₀ ≤ t < t₁) ? 1 : 0
a₁(t)⁽⁰⁾ = (t₁ ≤ t < t₂) ? 1 : 0
a₂(t)⁽⁰⁾ = (t₂ ≤ t < t₃) ? 1 : 0
a₃(t)⁽⁰⁾ = (t₃ ≤ t < t₄) ? 1 : 0
   :           :
a₃₊ₖ(t)⁽⁰⁾ = (t₃₊ₖ ≤ t ≤ t₄₊ₖ) ? 1 : 0

[layer k]
a₀(t)⁽ᵏ⁾ = (t-t₀)/(t₀₊ₖ-t₀) a₀(t)⁽ᵏ⁻¹⁾ + (t₁₊ₖ-t)/(t₁₊ₖ-t₁) a₁(t)⁽ᵏ⁻¹⁾
a₁(t)⁽ᵏ⁾ = (t-t₁)/(t₁₊ₖ-t₁) a₁(t)⁽ᵏ⁻¹⁾ + (t₂₊ₖ-t)/(t₂₊ₖ-t₂) a₂(t)⁽ᵏ⁻¹⁾
a₂(t)⁽ᵏ⁾ = (t-t₂)/(t₂₊ₖ-t₂) a₂(t)⁽ᵏ⁻¹⁾ + (t₃₊ₖ-t)/(t₃₊ₖ-t₃) a₃(t)⁽ᵏ⁻¹⁾
a₃(t)⁽ᵏ⁾ = (t-t₃)/(t₃₊ₖ-t₃) a₃(t)⁽ᵏ⁻¹⁾ + (t₄₊ₖ-t)/(t₄₊ₖ-t₄) a₄(t)⁽ᵏ⁻¹⁾

曲線的平滑程度（多項式最高次方）為n+k-1。

曲線座標公式
x(t) = a₀(t)⁽ᵏ⁾ x₀ + a₁(t)⁽ᵏ⁾ x₁ + a₂(t)⁽ᵏ⁾ x₂ + a₃(t)⁽ᵏ⁾ x₃

演算法（de Boor's algorithm）

平移的三角金字塔。

相鄰的k條線段，找到對應的樞紐點區間，求得比例。相鄰的k條線段，按比例取點，依序連線；遞推下去，得到一點。

窮舉tᵢ≤t≤tᵢ₊ₖ₊₁，連成一段曲線。窮舉每一條線段i，取得後方相鄰的k條線段，連成整條曲線。

B-spline curve進階主題

degree elevation、Greville abscissae。

《Bézier and B-Spline Techniques》

non-uniform rational B-spline curve（NURBS curve）

形容詞non-uniform：樞紐點非均勻、樞紐點不等距。

樞紐點越靠近，曲線越靠近控制點。

形容詞rational：追加控制點Z座標，求得曲線Z座標，最後曲線座標改成(X/Z, Y/Z)，即是「齊次座標」。

以便形成封閉曲線，例如圓形、橢圓形。方便實施射影變換。

UVa 12565

NURBS curve實際應用

工業繪圖軟體習慣使用NURBS curve。

NURBS curve涵蓋了Bézier curve所有特性。

surface

「曲面」或「表面」。形狀隨意的面。

parametric surface

曲線，一個參數t。曲面，兩個參數u和v。

{ x(u,v) = u - sin(u) cosh(v)
{ y(u,v) = 1 - cos(u) cosh(v)

代入(u,v) = (-0.1,0)，得到一個座標(x(-0.1,0), y(-0.1,0)) = (-0.0001,0.005)
代入(u,v) = (0,0)   ，得到一個座標(x(0,0)   , y(0,0)   ) = (0,0)
代入(u,v) = (0.1,0) ，得到一個座標(x(0.1,0) , y(0.1,0) ) = (0.0001,0.005)

二維曲面，使用兩個函數。三維曲面，使用三個函數。

polynomial surface

使用多項式函數。

引入control point以操控曲面

參數u負責橫向曲線，參數v負責縱向曲線。

建立N×M個控制點。先算橫向：每N點以參數u求得橫向曲線上一點。再算縱向：方才得到的M個點以參數v求得縱向曲線上一點。

縱橫互不干涉，互相獨立。先橫再縱、先縱再橫，結果相同。

引入knot point以微調曲面

自由調整同一橫排的控制點們的參數u、同一直排的控制點們的參數v，不一定要等分。曲面仍然穿過所有控制點，但是曲面形狀會改變。

Bézier surface

建立4×4個控制點。計算方式同前。

順帶一提，有人將4×4個控制點所得到的面稱作patch，大量patch相互銜接之後才稱作surface。

NURBS surface

建立N×M個控制點。計算方式同前。

工業繪圖軟體習慣使用NURBS surface。

polyline

電腦擅於處理大量資料。與其處心積慮、用少量控制點製造曲線，不如直截了當、用大量控制點製造折線。法理上，根據微積分的極限概念，極短的、綿密的、大量的直線，可以逼近曲線。情理上，只要點數夠多，折線就足夠耐看了。

折線與多邊形的資料結構相同。封閉折線就是多邊形。

折線應用廣泛。例如Microsoft PowerPoint的徒手畫。寫程式實作時，不斷擷取當前滑鼠座標，自然而然形成折線。

mesh

曲線的離散化是折線，曲面的離散化是網格。

大量的平坦的多邊形連成一片。通常是三角形。或者是四邊形。

網格與多面體的資料結構相同。封閉網格就是多面體。

網格應用廣泛。例如三維模型經常使用網格。