大量point資料結構: k-dimensional tree
摘要
| build | build | search | orthogonal
| time | space | (ins/del) | range search
-----------+-------------+-------------+-----------+--------------
kd-tree | O(NlogN) | O(N) | O(logN) | O(N1-1/D + K)
range tree | O(Nlogᴰ⁻¹N) | O(Nlogᴰ⁻¹N) | O(logᴰN) | O(logᴰN + K)
k維樹
大量儲存多維平面上的點,並且依照地緣關係來排序。常縮寫為k-d tree、kd-tree。以下分別介紹一維和二維的情形。
一維kd-tree
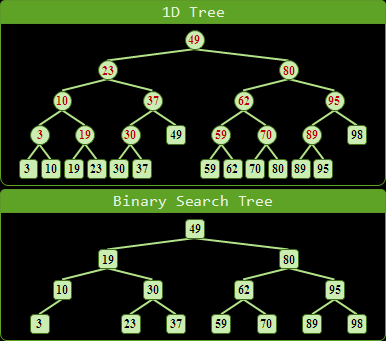
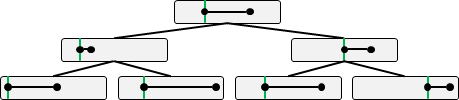
1d-tree的原理與binary search tree十分類似,但是長相卻有點不同。在1d-tree當中,資料全部集中在樹葉;得補一些數據到內部節點,才能做搜尋。
一維kd-tree:建立
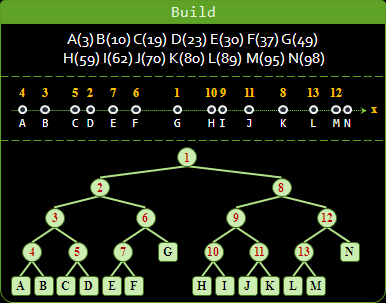
建立的方法,是把數線上的點分為左右兩等份,然後分別遞迴下去。習慣上是挑中位數位置的點作為分割點,分割點劃分於左側。
求分割點時,是使用時間為O(N)的求中位數演算法,而不是使用時間為O(NlogN)的排序演算法,才能達到理論上的時間複雜度。然而實際上排序演算法比較容易實作,效率也不錯。
時間複雜度O(NlogN),空間複雜度O(2N - 1) = O(N)。
一維kd-tree:插入、刪除、搜尋
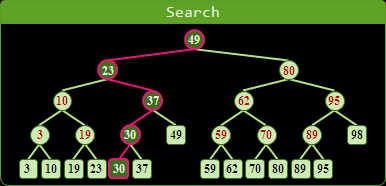
插入、刪除、搜尋的方式跟binary search tree的概念完全相同,時間複雜度都是O(logN)。
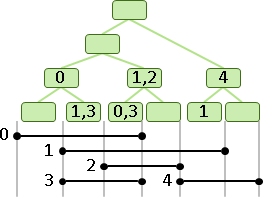
一維kd-tree:大範圍搜尋
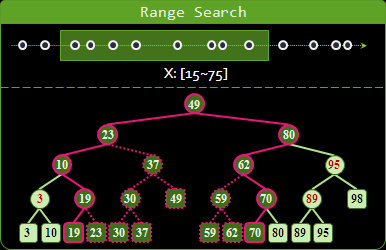
有一個重要的應用,是找出一個區間裡面所有的點。概念上是以搜尋範圍的左、右邊界值,分別搜尋一次,途中順便遍歷符合搜尋範圍內的子樹。
真正在實作時,則是同時以搜尋範圍的左、右邊界值進行搜尋:甲、如果搜尋完全落在分割點的其中一側,那麼就依照二元搜尋樹的規則繼續搜尋;乙、如果搜尋範圍橫跨分割點,那麼左右子樹都要搜尋;丙、如果搜尋範圍包含一整條分割區段,就可以直接遍歷整棵子樹,也可以當作是乙的情況來處理。
時間複雜度O(2logN + 2K-1) = O(logN + K),K為區間裡面的點數目。
延伸閱讀:另外一種建立一維kd-tree的方式
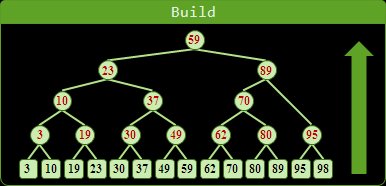
1d-tree另外有一種獨特的建樹方式:先排序所有資料,需時O(NlogN),然後再以bottom-up順序建立1d-tree,需時O(2N - 1) = O(N)。整體的時間複雜度仍相同。
讀者可能會想:既然要先排序,那乾脆就把資料放到陣列,排序完之後,直接二元搜尋不就好了,幹嘛需要1d-tree呢?你想的沒錯,一維的情況下,資料又不會變動時,的確沒有這個必要。
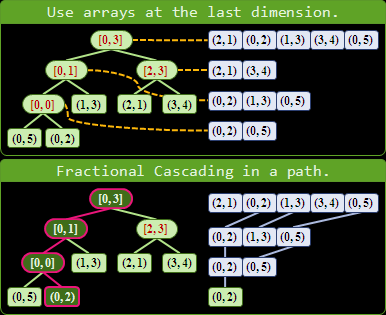
延伸閱讀:內部節點有兩種記錄方式
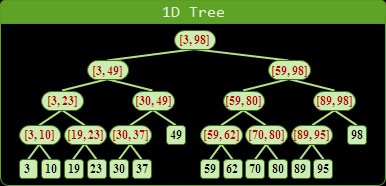
內部節點有兩種記錄方式。基本的方式是記錄分割點座標,這是仿照binary search tree的原理;進階的方式是記錄其下所有樹葉的數值範圍,實作起來會複雜一點。這兩種記錄方式也可以同時使用。
採用進階的方式有一個好處:可以允許樹葉當中有許多相同座標的點。如此一來,座標相同的點就能進行左右兩等份,閃避了分割點的二元搜尋規則。
一般來說,kd-tree沒有必要使用進階的方式。在range tree當中,才有必要用到進階的方式。
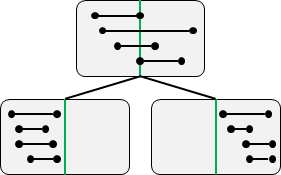
二維kd-tree
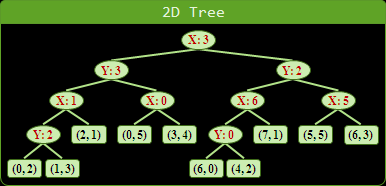
兩個維度依序作為等分的依據,輪流遞迴下去。
二維kd-tree:建立
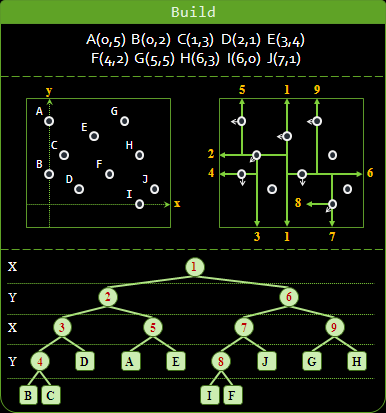
先以垂直線,把平面上的點分為左右兩等份,左右兩區域各自再以水平線,將平面上的點等分為上下兩等份。垂直、水平如此不斷輪流遞迴下去,直到每個區域都只剩一個點。
時間複雜度O(NlogN)。空間複雜度O(2N - 1) = O(N)。
二維kd-tree:插入、刪除、搜尋
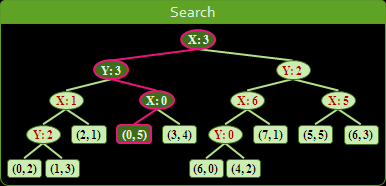
插入、刪除、搜尋的方式跟binary search tree的概念完全相同,時間複雜度都是O(logN)。
二維kd-tree:大範圍搜尋
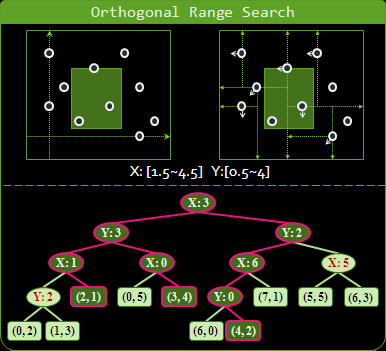
有一個重要的應用,是找出一個長方形範圍裡面所有的點:甲、如果搜尋範圍完全落在分割線的其中一側,那麼就依照二元搜尋樹的規則繼續搜尋;乙、如果搜尋範圍橫跨分割線,那麼左右子樹都要搜尋;丙、如果搜尋範圍包含一整塊分割區域,就可以直接遍歷整棵子樹,也可以當作是乙的情況來處理。
搜尋時,垂直方向最多遇到O(sqrtN)個區域,水平方向最多遇到O(sqrtN)個區域,時間複雜度O(2sqrtN + 2K-1) = O(sqrtN + K),K為長方形裡面的點數目。
高維kd-tree
建立時間為O(NlogN),建立空間為O(N),插入、刪除、搜尋的時間為O(logN),搜尋D體形範圍的時間為O(N1-1/D + K)。
ICPC 6041