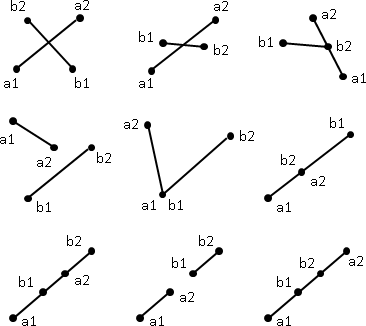
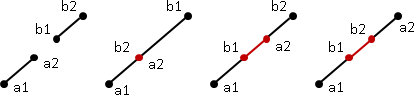
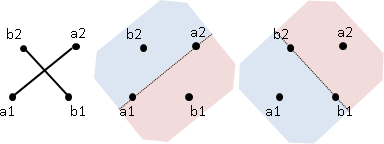
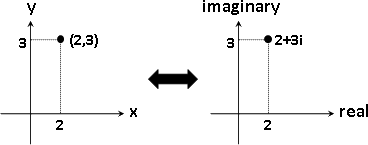
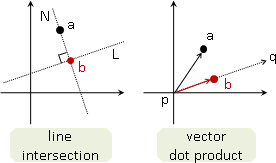
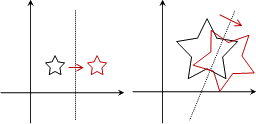
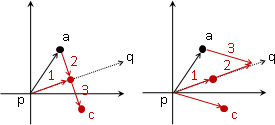
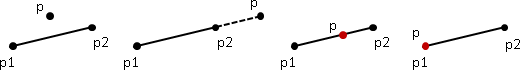vector product
點積與叉積
電腦實施運算,通常會有浮點數誤差。為了避免浮點數誤差,當使用電腦計算幾何問題,會採用不同於一般的數學公式和定理。
點積(dot product)、叉積(cross product)這兩個運算只有加減法和乘法,而不包括除法,能夠有效避免除法產生的浮點數誤差,另一方面也能夠減少計算時間。點積與叉積有著許多好用的特性,大部分的幾何問題,都可以運用點積與叉積來計算答案。
以下都是用二維空間當作範例。
資料結構
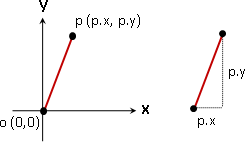
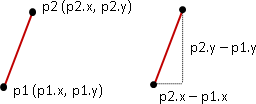
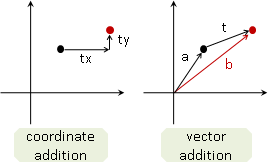
點積與叉積是向量運算,所以先設計一個向量的資料結構。
向量資料結構擁有一個座標,並且擁有一支點積函式與一支叉積函式。
兩個向量做點積的結果是一個純量。兩個向量做叉積的結果為一個向量。二維向量的情況下,叉積的結果只有第三個數值不是零。我們只會用到第三個數值,所以讓叉積函式的回傳值為純量。
點積、叉積跟長度的關係

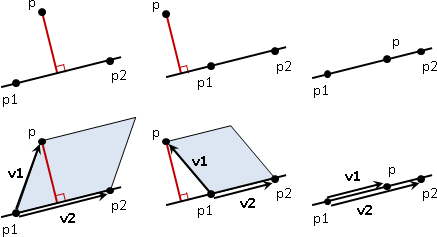
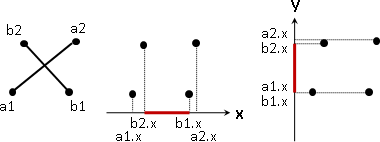
點積的結果為垂直投影的某種量。這某種量取絕對值,再除以底向量長度,得到底。
叉積的結果為平行四邊形的面積量。面積量取絕對值,再除以底向量長度,得到高。
點積、叉積跟角度的關係

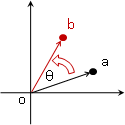
注意到acos與asin的回傳值,回傳的結果是弳度量(radian)而非度度量(grade),而且回傳值的範圍也不同。一般都以點積與acos求得介於0˚到180˚之間的夾角大小。
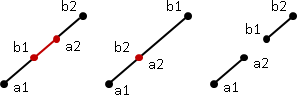
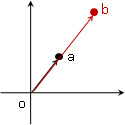
點積與向量夾角
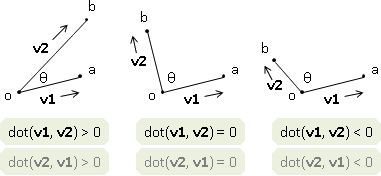
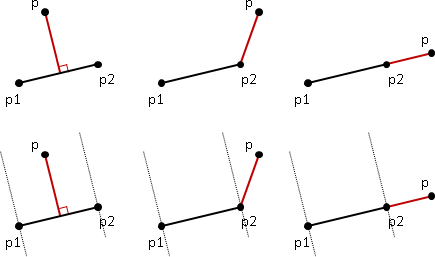
利用點積的性質,可以粗略判斷夾角大小:點積大於0時,兩向量夾角小於90˚;等於0時,夾角等於90˚;小於零時,夾角大於90˚且小於180˚。
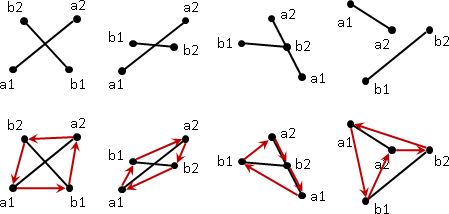
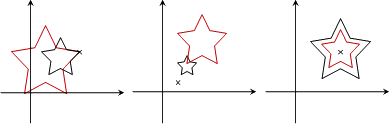
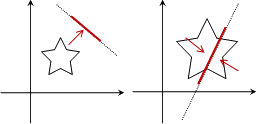
叉積與向量旋轉
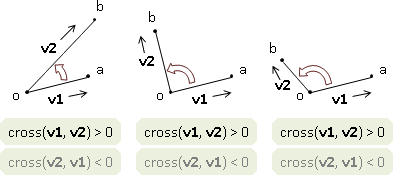
利用叉積的性質,可以粗略判斷夾角方向:叉積大於0時,兩向量前後順序為逆時針順序(在180˚之內);等於0時,兩向量平行,也就是指夾角等於0˚或180˚;小於0時,兩向量前後順序為順時針順序(在180˚之內)。
UVa 10445