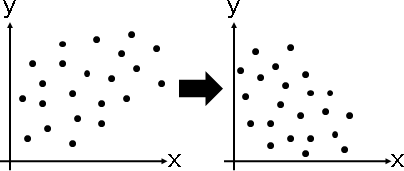
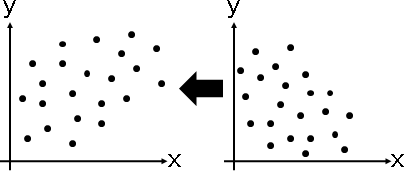
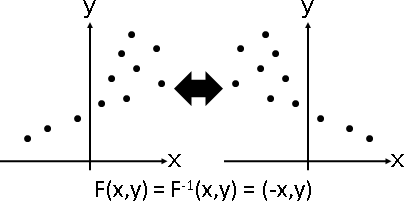
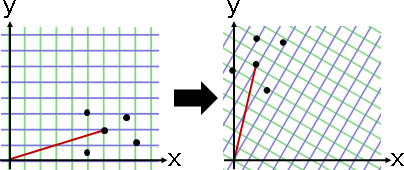
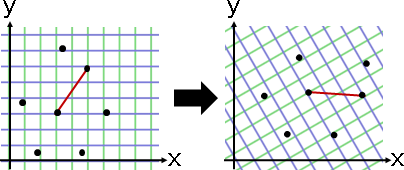
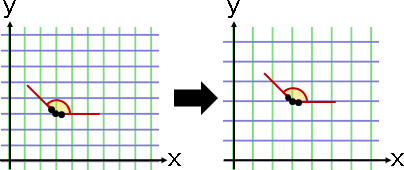
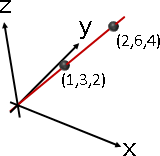
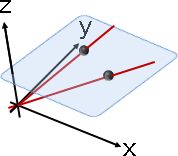
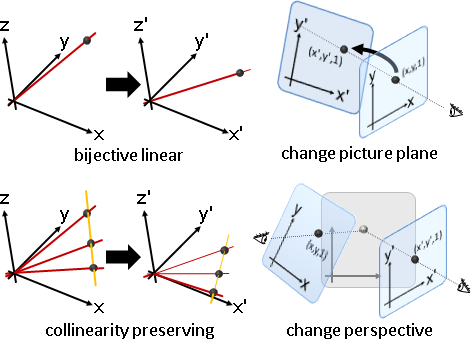
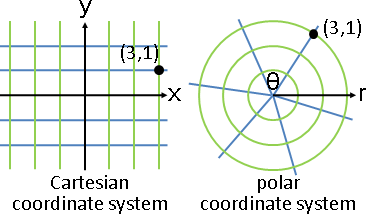
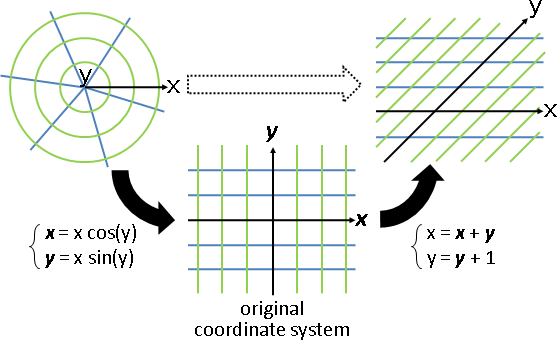
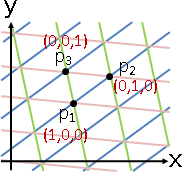
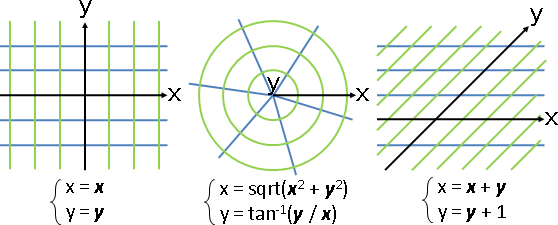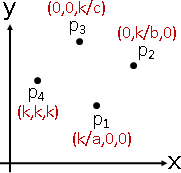linear transformation
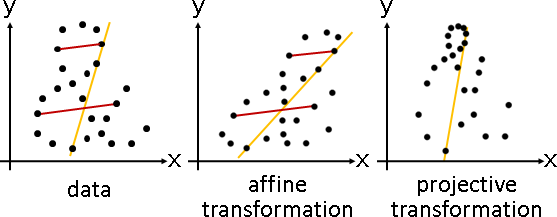
affine transformation
「線性變換」。變換時,採用線性函數。
「仿射變換」。變換時,採用仿射函數。
線性函數:加性函數、倍性函數
仿射函數:加性函數、倍性函數、常數項
linear function f affine function g
1. f(x + y) = f(x) + f(y) 1. f(x + y) = f(x) + f(y)
2. f(kx) = k f(x) 2. f(kx) = k f(x)
3. g(x) = f(x) + c
計算學傾向討論狹義版本。
狹義線性函數:變數加變數、變數乘常數
狹義仿射函數:變數加變數、變數乘常數、變數加常數
linear function affine function non-affine function
⎰ x̕ = x + 2y ⎰ x̕ = x + 2y + 1 ⎰ x̕ = xy
⎱ y̕ = 2(x + y) ⎱ y̕ = 2(x + y + 5) ⎱ y̕ = sin(x) + cos(y)
可以重新整理為標準形式。
狹義線性函數:變數乘上倍率,通通相加。
狹義仿射函數:線性函數,再加上常數項(平移)。
linear function affine function non-affine function
⎰ x̕ = x + 2y ⎰ x̕ = x + 2y + 1 ⎰ x̕ = xy
⎱ y̕ = 2x + 2y ⎱ y̕ = 2x + 2y + 5 ⎱ y̕ = sin(x) + cos(y)
可以重新整理為標準形式。向量版本。
狹義線性函數:任意矩陣
狹義仿射函數:任意矩陣→任意向量(平移)
linear transformation: x̕ = Ax
affine transformation: x̕ = Ax + b
representation of transformation【尚無正式名稱】
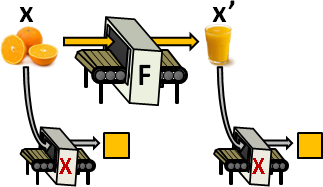
一筆數據的變換,可以寫成函數形式。
⎧ x̕ = fₓ(x,y,z) = ax + by + cz + p
⎨ y̕ = f(x,y,z) = dx + ey + fz + q
⎩ z̕ = f(x,y,z) = gx + hy + iz + r
x̕ F(x)
一筆數據的線性變換、仿射變換,可以寫成矩陣形式。
⎡ x̕ ⎤ ⎡ a b c ⎤ ⎡ x ⎤ ⎡ p ⎤
⎢ y̕ ⎥ = ⎢ d e f ⎥ ⎢ y ⎥ + ⎢ q ⎥
⎣ z̕ ⎦ ⎣ g h i ⎦ ⎣ z ⎦ ⎣ r ⎦
x̕ A x b
大量數據的線性變換、仿射變換,共兩種形式。
數學家:數據併成矩陣。
⎡ x̕₁ x̕₂ ⎤ ⎡ a b c ⎤ ⎡ x₁ x₂ ⎤ ⎡ p p ⎤
⎢ y̕₁ y̕₂ ... ⎥ = ⎢ d e f ⎥ ⎢ y₁ y₂ ... ⎥ + ⎢ q q ... ⎥
⎣ z̕₁ z̕₂ ⎦ ⎣ g h i ⎦ ⎣ z₁ z₂ ⎦ ⎣ r r ⎦
X̕ A X B
計算學家:數據併成向量,變換矩陣形成大型稀疏矩陣。
⎡ x̕₁ ⎤ ⎡ a b c 0 0 0 0 0 0 ... ⎤ ⎡ x₁ ⎤ ⎡ p ⎤
⎢ y̕₁ ⎥ ⎢ d e f 0 0 0 0 0 0 ... ⎥ ⎢ y₁ ⎥ ⎢ q ⎥
⎢ z̕₁ ⎥ ⎢ g h i 0 0 0 0 0 0 ... ⎥ ⎢ z₁ ⎥ ⎢ r ⎥
⎢ x̕₂ ⎥ = ⎢ 0 0 0 a b c 0 0 0 ... ⎥ ⎢ x₂ ⎥ + ⎢ p ⎥
⎢ y̕₂ ⎥ ⎢ 0 0 0 d e f 0 0 0 ... ⎥ ⎢ y₂ ⎥ ⎢ q ⎥
⎢ z̕₂ ⎥ ⎢ 0 0 0 g h i 0 0 0 ... ⎥ ⎢ z₂ ⎥ ⎢ r ⎥
⎢ : ⎥ ⎢ : : : : : : : : : ⎥ ⎢ : ⎥ ⎢ : ⎥
⎣ : ⎦ ⎣ : : : : : : : : : ⎦ ⎣ : ⎦ ⎣ : ⎦
x̕ A x b
homogeneous coordinates
仿射函數偽裝成線性函數。新添一個變數,只能代入1,乘在常數項。這個手法稱作「齊次座標」。
affine function homogeneous coordinates
⎰ x̕ = x + 2y + 1 ⎰ x̕ = x + 2y + 1z (z = 1)
⎱ y̕ = 2x + 2y + 5 ⎱ y̕ = 2x + 2y + 5z (z = 1)
換句話說。矩陣添加一個新維度,將常數項併入矩陣。數據隨之添加一個新維度,數值固定為1。這個手法稱作「齊次座標」。
affine function homogeneous coordinates
⎡ x̕ ⎤ ⎡ a b c ⎤ ⎡ x ⎤ ⎡ p ⎤ ⎡ x̕ ⎤ ⎡ a b c p ⎤ ⎡ x ⎤
⎢ y̕ ⎥ = ⎢ d e f ⎥ ⎢ y ⎥ + ⎢ q ⎥ ⎢ y̕ ⎥ = ⎢ d e f q ⎥ ⎢ y ⎥
⎣ z̕ ⎦ ⎣ g h i ⎦ ⎣ z ⎦ ⎣ r ⎦ ⎢ z̕ ⎥ ⎢ g h i r ⎥ ⎢ z ⎥
x̕ A x b ⎣ 1 ⎦ ⎣ 0 0 0 1 ⎦ ⎣ 1 ⎦
x̕ₕ Aₕ xₕ
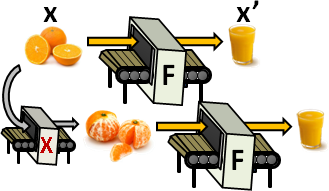
優點:多個仿射變換可以複合成一個仿射變換,只需儲存一個變換矩陣。缺點:實施變換,計算步驟較多。
differentiation of transformation【尚無正式名稱】
給定變換函數,可以利用微分,求得變換矩陣。
d/dx (ax + b) = a。一次函數實施微分,得到首項係數。
d/dx (Ax + b) = Aᵀ。輸入推廣成向量,係數推廣成矩陣。
線性變換函數、仿射變換函數,微分並轉置,得到變換矩陣。
affine transformation
(x̕,y̕,z̕) = F(x,y,z)
function representation
⎧ x̕ = fₓ(x,y,z) = ax + by + cz + p
⎨ y̕ = f(x,y,z) = dx + ey + fz + q
⎩ z̕ = f(x,y,z) = gx + hy + iz + r
matrix representation
⎡ x̕ ⎤ ⎡ a b c ⎤ ⎡ x ⎤ ⎡ p ⎤
⎢ y̕ ⎥ = ⎢ d e f ⎥ ⎢ y ⎥ + ⎢ q ⎥
⎣ z̕ ⎦ ⎣ g h i ⎦ ⎣ z ⎦ ⎣ r ⎦
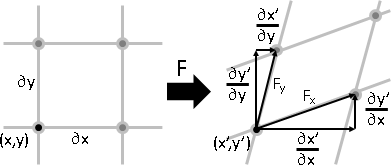
transpose of derivative is transformation matrix
⎡ ∂/∂x fₓ ∂/∂y fₓ ∂/∂z fₓ ⎤ ⎡ a b c ⎤
F′(x,y,z)ᵀ = J = ⎢ ∂/∂x f ∂/∂y f ∂/∂z f ⎥ = ⎢ d e f ⎥
⎣ ∂/∂x f ∂/∂y f ∂/∂z f ⎦ ⎣ g h i ⎦
微分並轉置,就是Jacobian matrix。導致大家鮮少講「transformation matrix」,數學家習慣講「Jacobian matrix of transformation」,物理學家習慣講「deformation gradient」。
derivative: F′ = ∇F = Jᵀ = Aᵀ
transformation matrix: F′ᵀ = ∇Fᵀ = J = A
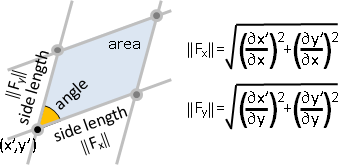
Dirichlet energy: ‖F′‖ꜰ² = ‖∇F‖ꜰ² = ‖J‖ꜰ² = ‖A‖ꜰ²
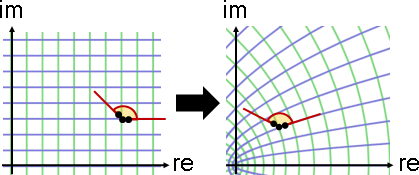
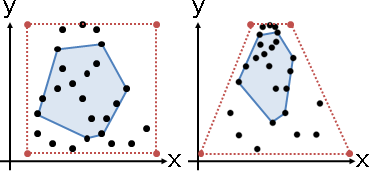
approximation of transformation【尚無正式名稱】
一般的變換,通常無法求出最近似仿射變換。
標準做法是誤差盡量小。原本變換與最近似仿射變換,兩者的輸出的平方誤差,所有輸入通通計入。
誤差總和通常是無限大,最小值通常是不存在。
min sum ‖F(x) - Ax‖²
A x
一般的變換,只能求出局部的最近似仿射變換。
泰勒級數於特定點展開,一階係數(Jacobian matrix)作為變換矩陣,剩餘部分作為平移向量。
Taylor series at (xₒ,yₒ,zₒ)
⎡ x-xₒ ⎤
F(x,y,z) = F(xₒ,yₒ,zₒ) + F′(x,y,z)ᵀ ⎢ y-yₒ ⎥ + ...
⎣ z-zₒ ⎦
^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^
order 0 order 1
⎡ x ⎤ ⎡ xₒ ⎤
F(x,y,z) = F′(x,y,z)ᵀ ⎢ y ⎥ + F(xₒ,yₒ,zₒ) - F′(x,y,z)ᵀ ⎢ yₒ ⎥ + ...
⎣ z ⎦ ⎣ zₒ ⎦
^^^^^^^^^^ ^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
A x b
transformation matrix A: F′(x)ᵀ = J
translation vector b: F(x) - F′(x)ᵀx = F(x) - Jx
一、最近似線性變換矩陣:變換函數,微分並轉置(Jacobian matrix)。
二、最近似平移向量:變換函數,減去最近似線性變換。
最近似線性變換矩陣,恰好也是Jacobian matrix。太棒了!
我不確定平方誤差是否最小。【尚待確認】
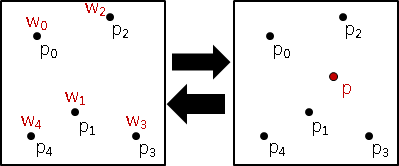
decomposition of transformation【尚無正式名稱】
變換矩陣可以分解,得到富有意義的矩陣們。
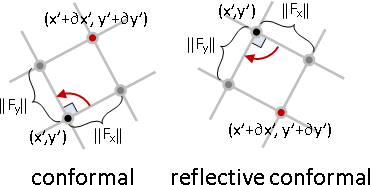
奇異值分解,得到旋轉鏡射矩陣、縮放矩陣、旋轉鏡射矩陣。
SVD(J) = UΣVᵀ
U and Vᵀ are rotation/reflection. (orthonormal)
Σ is scaling. (diagonal matrix)
極分解,得到旋轉鏡射矩陣、可正交對角化矩陣。
polar(J) = RS
R = UVᵀ is rotation/reflection. (orthonormal)
S = VΣVᵀ is orthogonally diagonalizable. (symmetric positive semidefinite)
另一種極分解,得到可正交對角化矩陣、旋轉鏡射矩陣。
polar(J) = SR
S = UΣUᵀ is orthogonally diagonalizable. (symmetric positive semidefinite)
R = UVᵀ is rotation/reflection. (orthonormal)
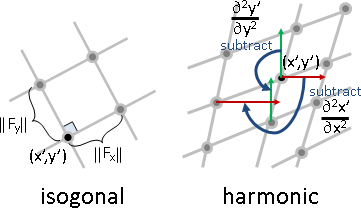
奇偶分解,得到主縮放矩陣、主旋轉矩陣。【尚待確認】
even(J) = (J + Jᵀ) / 2 is principal scaling. (symmetric)
odd(J) = (J - Jᵀ) / 2 is principal rotation. (skew-symmetric)
經典的線性變換、仿射變換
大家經常使用仿射變換。優點是只有加法與倍率,相當單純,擁有漂亮數學性質,擁有高速演算法。缺點是單純導致功效不彰。期待大家發明更特別的變換!
單一數據的變換:平移translate、縮放scale、旋轉rotate、投影project、鏡射reflect。請見本站文件「transformation」。
全體數據的變換:中心化centering、標準化standardization、白化whitening。請見本站文件「correlation」。
局部數據的變換:均值mean filter、鄰差difference filter、加權平均weighted average filter。請見本站文件「filter」。