regression

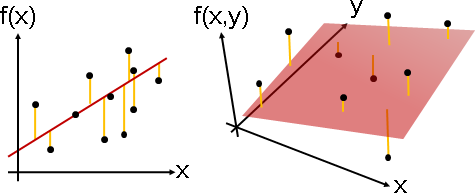
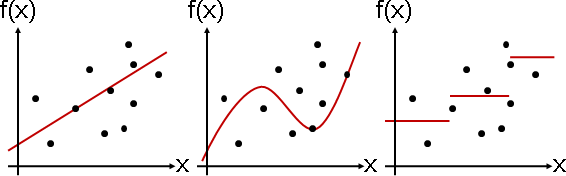
「迴歸」就是找一個函數，盡量符合手邊的一堆函數點。此函數稱作「迴歸函數」。

方便起見，以下用座標表示函數點。

error（loss）

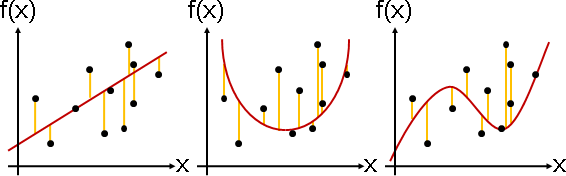
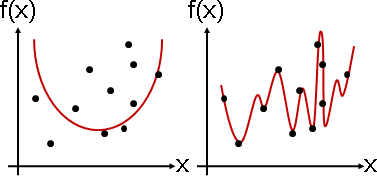
強硬地用函數符合函數點，就會有「誤差」。

單一函數點的誤差，有許多種衡量方式，一般是用函數點與函數的差的平方（平方誤差），其他還有函數點與函數的差的絕對值（絕對值誤差）。

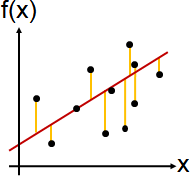
regression化作optimization

人腦考慮的「最符合」，放到了電腦就被設定成「誤差總和最小」。把誤差總和寫成一個函數，迴歸問題就變成了最佳化問題！

運用最佳化演算法，求得誤差最小值，求得迴歸函數的係數。

迴歸函數
f(x) = ax² + bx + c
N個函數點
(x₀,y₀) ... (xɴ₋₁,yɴ₋₁)
每個函數點的平方誤差
(y₀ - f(x₀))² ... (yɴ₋₁ - f(xɴ₋₁))²
所有函數點的平方誤差總和
e(a,b,c) = (y₀ - f(x₀))² + ... + (yɴ₋₁ - f(xɴ₋₁))²
         = ∑ (yᵢ - f(xᵢ))²
         = ∑ (yᵢ - ŷᵢ)²
         = ∑ ‖yᵢ - ŷᵢ‖²
令誤差總和最小
 min e(a,b,c)
^a,b,c
選定一個最佳化演算法，求出e(a,b,c)的最小值，求出此時a b c的數值，
就得到迴歸函數f(x)。

迴歸函數
f(x) = ax² + bx + c
N個函數點
(2,3) ... (7,8)
每個函數點的平方誤差
  (3 - f(2))² ... (8 - f(7))²
= (3 - (a⋅2² + b⋅2 + c))² ... (8 - (a⋅7² + b⋅7 + c))²
所有函數點的誤差總和
  (3 - f(2))² + ... + (8 - f(7))²
= (3 - (a⋅2² + b⋅2 + c))² + ... + (8 - (a⋅7² + b⋅7 + c))²

squared error / absolute error

平方誤差後盾雄厚，絕對值誤差樸實無華。大家採用平方誤差。

因為平方誤差非常實用，所以許多人將「採用平方誤差、令誤差總和最小」直接稱作「最小平方法least squares method」。

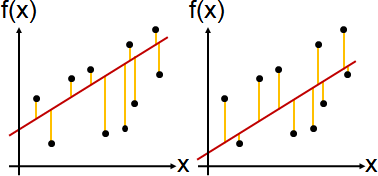
一、平方誤差通常有唯一解。絕對值誤差通常有無限多解。

絕對值誤差當中，當迴歸函數上下函數點不一樣多，那麼迴歸函數將朝向函數點較少的一側移動，降低絕對值誤差。當迴歸函數上下函數點一樣多，那麼迴歸函數可以上下移動，絕對值誤差保持相同。

絕對值誤差當中，答案總是均分函數點，答案可能不唯一。這種符合方式太過樸素、缺乏內涵。答案其實就是中位數。

二、平方誤差支援微積分，容易推導數學公式。

微積分經典定理：「極值位於一次微分等於零的地方」。藉由一次微分，得以判別誤差函數最小值，甚至得以推導公式。

平方誤差函數，處處皆可一次微分。絕對值誤差函數，至少有一處無法一次微分，只能改用次微分，事情變得相當複雜。

三、平方誤差支援線性代數，擁有強悍數學性質。

線性代數經典定理：「平方誤差盡量小＝垂直投影」。藉由垂直投影，得以推導公式，讓這種符合方式擁有了具體形象。

當誤差函數既是平方誤差函數、又是線性函數，那麼可以使用線性代數。絕對值誤差函數則無法使用線性代數。

polynomial regression

linear regression

「一次迴歸」。迴歸函數採用一次函數。誤差採用平方誤差。

一個變數，迴歸函數是直線。兩個變數，迴歸函數是平面。

一次迴歸性質特殊，不需要最佳化演算法。寫成「linear least squares」，套用「normal equation」，求得迴歸函數的係數。

一次迴歸可以改寫成一次方程組。

迴歸函數 f(x) = ax + b
函數點 (2,3) (5,6) (7,8)
⎡ 2  1 ⎤ ⎡ a ⎤   ⎡ 3 ⎤
⎢ 5  1 ⎥ ⎣ b ⎦ = ⎢ 6 ⎥
⎣ 7  1 ⎦         ⎣ 8 ⎦
   A       x       y

迴歸函數 f(x,y) = ax + by + c  
函數點 (2,3,4) (5,6,7) (7,8,9) (3,3,3) (4,4,4)
⎡ 2  3  1 ⎤         ⎡ 4 ⎤
⎢ 5  6  1 ⎥ ⎡ a ⎤   ⎢ 7 ⎥
⎢ 7  8  1 ⎥ ⎢ b ⎥ = ⎢ 9 ⎥
⎢ 3  3  1 ⎥ ⎣ c ⎦   ⎢ 3 ⎥
⎣ 4  4  1 ⎦         ⎣ 4 ⎦
     A        x       y

一次迴歸可以改寫成最佳化問題。

所有函數點的誤差總和 ‖Ax - y‖²
一次迴歸化作最佳化問題 min ‖Ax - y‖²

一次迴歸的公式解是normal equation，無解版本。

最佳化問題的解 x = (Aᵀ A)⁻¹ Aᵀ y

函數點足夠多，導致A是瘦矩陣，導致Ax = y是超定方程組。函數點皆相異，導致超定即無解【待補證明】。因此x是無解版本的normal equation。

超定：等式多於變數row(A) > column(A)，無解：原矩陣和擴充矩陣維度不相等rank(A) ≠ rank([A|b])，兩者毫無關聯。不幸的是，中學數學教科書將兩者視作相同，成為歷史共業。

一次迴歸的公式解可以改寫成共變異數的比值。

x = cov(x, y) / cov(x, x)

一次迴歸可以找到輸入與輸出的大致關係：成正比、成反比。首項係數a的正負，代表正反比。

polynomial regression

「多項式迴歸」。迴歸函數採用多項式函數。誤差採用平方誤差。

演算法仍是normal equation。

迴歸函數 f(x) = ax + b
函數點 (2,3) (5,6) (7,8)
⎡ 2  1 ⎤ ⎡ a ⎤   ⎡ 3 ⎤
⎢ 5  1 ⎥ ⎣ b ⎦ = ⎢ 6 ⎥
⎣ 7  1 ⎦         ⎣ 8 ⎦

迴歸函數 f(x) = ax² + bx + c
函數點 (2,3) (5,6) (7,8)
⎡  4  2  1 ⎤ ⎡ a ⎤   ⎡ 3 ⎤
⎢ 25  5  1 ⎥ ⎢ b ⎥ = ⎢ 6 ⎥
⎣ 49  7  1 ⎦ ⎣ c ⎦   ⎣ 8 ⎦

迴歸函數 f(x,y) = ax² + bxy + cy² + dx + ey + f
函數點 (2,3,4) (5,6,7) (7,8,9)
                         ⎡ a ⎤
⎡ 2²  2×3  3²  2  3  1 ⎤ ⎢ b ⎥   ⎡ 4 ⎤
⎢ 5²  5×6  6²  5  6  1 ⎥ ⎢ c ⎥ = ⎢ 7 ⎥
⎣ 7²  7×8  8²  7  8  1 ⎦ ⎢ d ⎥   ⎣ 9 ⎦
                         ⎢ e ⎥
                         ⎣ f ⎦

underfitting / overfitting

用單純的函數去符合複雜的函數點，顯然符合的不太完美。

用複雜的函數去符合單純的函數點，顯然事情被搞複雜了。

如果我們不清楚函數點的性質，也就無法抉擇函數了。那麼，該如何了解函數點的性質呢？這是心靈科學，就此打住。