interpolation
interpolation
「內插」就是找一個函數,完全符合手邊的一堆函數點。此函數稱作「內插函數」。
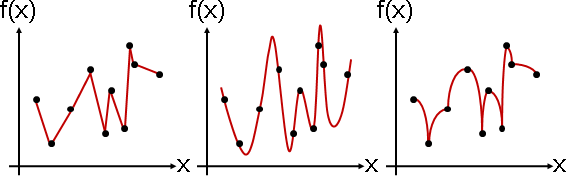
換句話說,找到一個函數,穿過所有給定的函數點。外觀就像是在相鄰的函數點之間,插滿函數點,因而得名「內插」。
方便起見,以下用座標表示函數點。

interpolation
interpolation
「內插」就是找一個函數,完全符合手邊的一堆函數點。此函數稱作「內插函數」。

換句話說,找到一個函數,穿過所有給定的函數點。外觀就像是在相鄰的函數點之間,插滿函數點,因而得名「內插」。
方便起見,以下用座標表示函數點。

polynomial interpolation
polynomial interpolation
「多項式內插」。內插函數採用多項式函數。
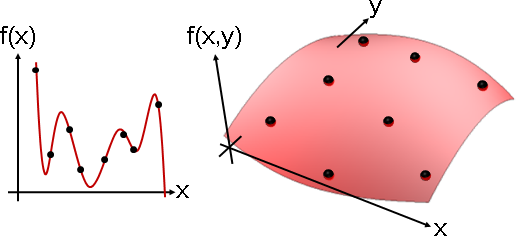
f = InterpolatingPolynomial[{{{2,5},3},{{5,4},4},{{6,7},2},{{1,2},1},{{4,2},0},{{0,4},3},{{2,6},2},{{9,1},1}},{x,y}]; Plot3D[f, {x, 0, 10}, {y, 0, 7}, PlotRange -> {-10, 10}, Boxed -> False, Axes -> False, Mesh->None, ColorFunction -> (ColorData["CherryTones"][Rescale[#3, {-2, 2}]] &) ]
給定N個函數點,找到N個多項式係數。
給定N個函數點 (x₀,f(x₀)) (x₁,f(x₁)) ... (xɴ₋₁,f(xɴ₋₁)) 內插函數是N項多項式函數(N-1次多項式函數) f(x) = c₀ + c₁ x¹ + ... + cɴ₋₁ xN-1 目標是找到N個係數 c₀ c₁ ... cɴ₋₁
unisolvence theorem
只有唯一一個N-1次多項式(N項多項式,某些項可以為零。講N項比較直覺),剛好符合N個相異函數點。
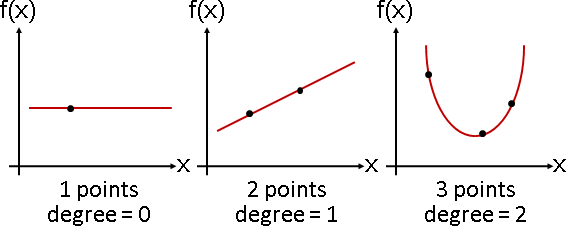
underfitting / overfitting
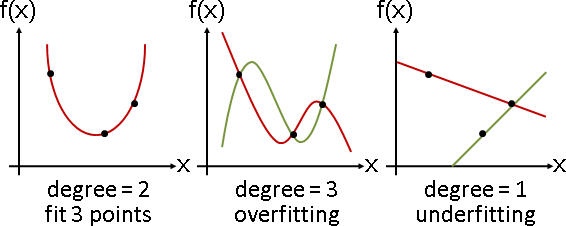
次方數(講項數比較直覺)不正確,就有許多種符合方式。
高於N項的多項式,太過符合N個相異函數點。存在許多種符合方式。
低於N項的多項式,無法符合N個相異函數點。不存在符合方式,除非運氣好。
演算法(Vandermonde matrix)
5個函數點 f(0) = 32, f(2) = 12, f(3) = 43, f(5) = 55, f(9) = 66 內插函數是4次多項式,一共5項 f(x) = c₀ x⁰ + c₁ x¹ + c₂ x² + c₃ x³ + c₄ x⁴ 內插就是滿足 f(0) = 0⁰ c₀ + 0¹ c₁ + 0² c₂ + 0³ c₃ + 0⁴ c₄ = 32 f(2) = 2⁰ c₀ + 2¹ c₁ + 2² c₂ + 2³ c₃ + 2⁴ c₄ = 12 f(3) = 3⁰ c₀ + 3¹ c₁ + 3² c₂ + 3³ c₃ + 3⁴ c₄ = 43 f(5) = 5⁰ c₀ + 5¹ c₁ + 5² c₂ + 5³ c₃ + 5⁴ c₄ = 55 f(9) = 9⁰ c₀ + 9¹ c₁ + 9² c₂ + 9³ c₃ + 9⁴ c₄ = 66 寫成一次方程組的模樣 ⎡ 0⁰ 0¹ 0² 0³ 0⁴ ⎤ ⎡ c₀ ⎤ ⎡ 32 ⎤ ⎢ 2⁰ 2¹ 2² 2³ 2⁴ ⎥ ⎢ c₁ ⎥ ⎢ 12 ⎥ ⎢ 3⁰ 3¹ 3² 3³ 3⁴ ⎥ ⎢ c₂ ⎥ = ⎢ 43 ⎥ ⎢ 5⁰ 5¹ 5² 5³ 5⁴ ⎥ ⎢ c₃ ⎥ ⎢ 55 ⎥ ⎣ 9⁰ 9¹ 9² 9³ 9⁴ ⎦ ⎣ c₄ ⎦ ⎣ 66 ⎦ 求得多項式係數 -1 ⎡ c₀ ⎤ ⎡ 0⁰ 0¹ 0² 0³ 0⁴ ⎤ ⎡ 32 ⎤ ⎢ c₁ ⎥ ⎢ 2⁰ 2¹ 2² 2³ 2⁴ ⎥ ⎢ 12 ⎥ ⎢ c₂ ⎥ = ⎢ 3⁰ 3¹ 3² 3³ 3⁴ ⎥ ⎢ 43 ⎥ ⎢ c₃ ⎥ ⎢ 5⁰ 5¹ 5² 5³ 5⁴ ⎥ ⎢ 55 ⎥ ⎣ c₄ ⎦ ⎣ 9⁰ 9¹ 9² 9³ 9⁴ ⎦ ⎣ 66 ⎦ 多項式係數有唯一解的條件,就是x=0,2,3,5,9是五個不同數字。
N個函數
(x₀ f(x₀)), (x₁ f(x₁)), ... , (xɴ₋₁ f(xɴ₋₁))
內插函數
f(x) = c₀ + c₁ x¹ + ... + cɴ₋₁ xᴺ⁻¹
內插就是滿足
f(x₀) = c₀ + c₁ x₀¹ + ... + cɴ₋₁ x₀ᴺ⁻¹
f(x₁) = c₀ + c₁ x₁¹ + ... + cɴ₋₁ x₁ᴺ⁻¹
: :
f(xɴ₋₁) = c₀ + c₁ xɴ₋₁¹ + ... + cɴ₋₁ xɴ₋₁ᴺ⁻¹
寫成一次方程組的模樣
⎡ 1 x₀¹ .. x₀ᴺ⁻¹ ⎤ ⎡ c₀ ⎤ ⎡ f(x₀) ⎤
⎢ 1 x₁¹ .. x₁ᴺ⁻¹ ⎥ ⎢ c₁ ⎥ ⎢ f(x₁) ⎥
⎢ : : : ⎥ ⎢ : ⎥ = ⎢ : ⎥
⎢ : : : ⎥ ⎢ : ⎥ ⎢ : ⎥
⎣ 1 xɴ₋₁¹ .. xɴ₋₁ᴺ⁻¹ ⎦ ⎣ cɴ₋₁ ⎦ ⎣ f(xɴ₋₁) ⎦
A c = y
向量c有唯一解的條件,就是x₀到xɴ₋₁都不同。
換句話說,一開始給定的N個函數點,X座標都不同。
順便證明了unisolvence theorem。
十分漂亮的公式解,時間複雜度等同高斯消去法O(N³)。
數值N次方,一下子就溢位了;數值範圍很大,解方程組易生誤差。因此這個公式解並不實用。
UVa 12143 12339
演算法(Lagrange interpolation)
Plot[(12(x-0)(x-3)(x-5)(x-9))/((2-0)(2-3)(2-5)(2-9)), {x, -1, 10}, PlotRange -> {-50,50}, Axes -> False, Mesh -> None]
Plot[InterpolatingPolynomial[{{0,32}, {2,12}, {3,43}, {5,55}, {9,66}}, x], {x, -1, 10}, PlotRange -> {-60,60}, Axes -> False, Mesh -> None]
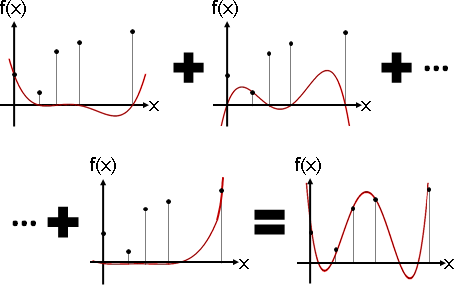
製作N個N-1次多項式函數,第一個只穿過第一點、其餘點為零,第二個只穿過第二點、其餘點為零,以此類推。相加起來,仍是N-1次多項式函數,而且穿過所有點──正是內插函數。
N-1 x - xⱼ
f(x) = ∑ yᵢ ∏ —————————
i=0 j≠i xᵢ - xⱼ
f(0) = 32, f(2) = 12, f(3) = 43, f(5) = 55, f(9) = 66
(x-2)(x-3)(x-5)(x-9)
F₀(x) = 32 ⋅ ————————————————————————— 只有代入x=0會等於32,
(0-2)(0-3)(0-5)(0-9) 代入x=2,3,5,9皆是0。
(x-0) (x-3)(x-5)(x-9)
F₁(x) = 12 ⋅ ————————————————————————— 只有代入x=2會等於12,
(2-0) (2-3)(2-5)(2-9) 代入x=0,3,5,9皆是0。
(x-0)(x-2) (x-5)(x-9)
F₂(x) = 43 ⋅ —————————————————————————
(3-0)(3-2) (3-5)(3-9)
(x-0)(x-2)(x-3) (x-9)
F₃(x) = 55 ⋅ —————————————————————————
(5-0)(5-2)(5-3) (5-9)
(x-0)(x-2)(x-3)(x-5)
F₄(x) = 66 ⋅ —————————————————————————
(9-0)(9-2)(9-3)(9-5)
f(x) = F₀(x) + F₁(x) + F₂(x) + F₃(x) + F₄(x) 即為所求
時間複雜度分析如下:
一、先備知識:多項式乘法、多項式除法,O(N²)。
二、分子:連乘N項,然後分別除以第一項到第N項,分別得到每道多項式函數的分子。O(N³)。
三、分母與倍率:每道多項式函數分別處理。連乘分母,然後多項式函數的N個係數,分別除以分母。O(N²)。
四、加總:所有多項式函數,對應項係數相加。O(N²)。
時間複雜度O(N³)。
求得內插函數,顯然非常麻煩!偷懶的方式是不求內插函數,而是直接代入x的數值,時間複雜度O(N²)。
總結一下。求得內插函數為O(N³),內插函數求值為O(N)。不求內插函數,直接求值為O(N²)。
演算法(Newton interpolation)
Lagrange interpolation改成online版本。
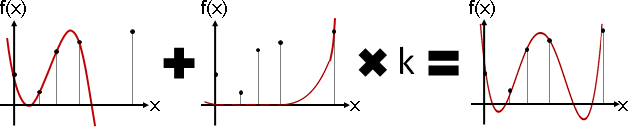
遞推法,逐次加入一個新的函數點,即時更新內插函數。一、穿過前n點的內插函數;二、製作只穿過第n+1點,而前n點都是零的函數。兩個函數相加即可。
因為相加之後要穿過第n+1點,所以第二個函數必須調整倍率,以便抵銷第一個函數在第n+1點的影響。
F₀(x) = y₀
i x - xⱼ
Fᵢ₊₁(x) = Fᵢ(x) + (yᵢ₊₁ - Fᵢ(xᵢ₊₁)) ⋅ ∏ ———————————
j=0 xᵢ₊₁ - xⱼ
Fɴ₋₁(x) 即為所求
f(0) = 32, f(2) = 12, f(3) = 43, f(5) = 55, f(9) = 66
F₀(x) = 32
(x-0) (x-3)(x-5)(x-9)
F₁(x) = F₀(x) + (12 - F₀(2)) ⋅ —————————————————————————
(2-0) (2-3)(2-5)(2-9)
(x-0)(x-2) (x-5)(x-9)
F₂(x) = F₁(x) + (43 - F₁(3)) ⋅ —————————————————————————
(3-0)(3-2) (3-5)(3-9)
(x-0)(x-2)(x-3) (x-9)
F₃(x) = F₂(x) + (55 - F₂(5)) ⋅ —————————————————————————
(5-0)(5-2)(5-3) (5-9)
(x-0)(x-2)(x-3)(x-5)
F₄(x) = F₃(x) + (66 - F₃(9)) ⋅ ————————————————————————— 即為所求
(9-0)(9-2)(9-3)(9-5)
總結一下。求得內插函數O(N³),內插函數求值O(N)。不求內插函數,直接求值,則是O(N²)。
演算法(Neville interpolation)
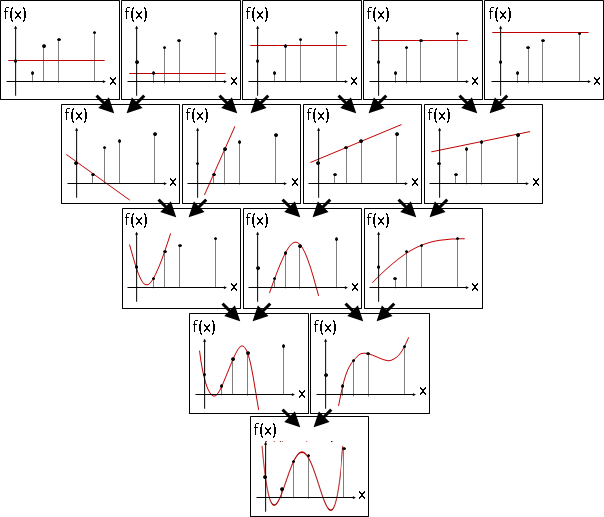
兩個函數,選兩處x值並且實施一次內插,得到一個函數。
每個函數點分別建立常數函數(零次多項式函數)。兩個零次多項式函數,一次內插,得到一次多項式函數,穿過兩個函數點。兩個一次多項式函數,一次內插,得到二次多項式函數,穿過三個函數點。以此類推。
注意到,以上這些演算法,函數點都不需要按照座標大小排序。
Fᵢᵢ(x) = yᵢ for i = 0...N-1
(xⱼ - x) Fᵢ ⱼ₋₁(x) + (x - xᵢ) Fᵢ₊₁ ⱼ(x)
Fᵢⱼ(x) = —————————————————————————————————————————
(xⱼ - x) + (x - xᵢ)
f(x) = F₀ ɴ₋₁(x) 即為所求
dynamic programming,子問題是區間,每個子問題[i,j]源自兩個子問題[i-1,j]與[i,j-1],子問題總共O(N²)個。解決一個子問題,需要多項式倍率、多項式加法,時間複雜度O(N)。總時間複雜度O(N³)。
總結一下。求得內插函數為O(N³),內插函數求值為O(N)。不求內插函數,直接求值為O(N²)。
Runge's phenomenon
多項式內插有個缺點:函數曲線抖動。
為了緩和曲線,以下繼續介紹其他內插演算法。
piecewise polynomial interpolation
nearest neighbor interpolation
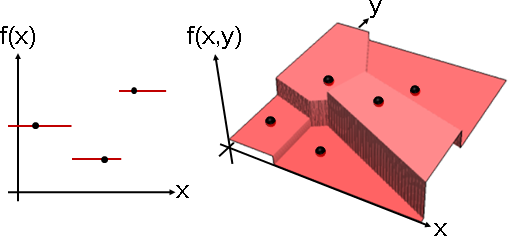
「近鄰內插」。內插函數是許多個零次多項式。
Plot3D[Nearest[{{2,5},{5,4},{6,7},{1,2},{4,2}}->{3,4,2,1,0}, {x,y}], {x,0,10}, {y,0,10}, ColorFunction -> "Rainbow"]
n = Nearest[{{2,5},{5,4},{6,7},{1,2},{4,2}}->{3,4,2,1,0}]; Plot3D[n[{x,y}], {x,0,10}, {y,0,10}, PlotRange -> {0, 8}, Boxed -> False, Axes -> False, Mesh -> None, NormalsFunction -> None, PlotPoints -> 100, ColorFunction -> (ColorData["CherryTones"][Rescale[#3, {-4, 4}]] &)]
根據輸入值,找到最接近的函數點,取其輸出值。俯瞰即「Voronoi diagram」。
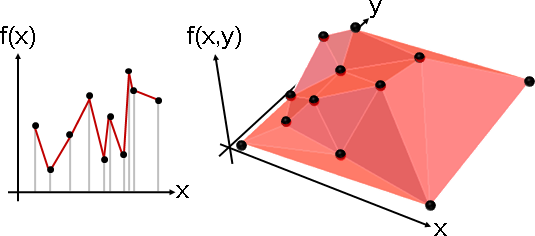
linear interpolation
「一次內插」。內插函數是許多個一次多項式。
p = {{2,3,3},{5,4,5},{6,6,6},{1,2,1},{4,2,0},{0,4,1},{1,7,1},{0,7,4},{10,10,2},{0,0,1},{0,10,2},{9,1,0}}; m = DelaunayMesh[ p[[All,1;;2]] ]; r = MeshRegion[p, Style[MeshCells[m, 2], {ColorData["CherryTones"][0.5], EdgeForm[Directive[Pink]]}]]; Show[ Plot3D[0, {x, 0, 10}, {y, 0, 10}, PlotRange -> {0, 7}, PlotStyle -> Opacity[0], BoundaryStyle -> None, Boxed -> False, Axes -> False, Mesh -> None], r ]
p = {{2,3,3},{5,4,5},{6,6,6},{1,2,1},{4,2,0},{0,4,1},{1,7,1},{0,7,4},{10,10,2},{0,0,1},{0,10,2},{9,1,0}}; q = Transpose[{ p[[All,1;;2]] , p[[All,3]] }]; f = Interpolation[q, InterpolationOrder->1]; Plot3D[f[x,y], {x, 0, 10}, {y, 0, 10}, PlotRange -> {0, 7}, Boxed -> False, Axes -> False, Mesh -> None, PlotPoints -> 100, ColorFunction -> (ColorData["CherryTones"][Rescale[#3, {-4, 4}]] &)]
輸入值相鄰的函數點,以直線連接。俯瞰即「triangulation」,有許多種選擇,其中最美觀的是Delaunay triangulation。
以「相似三角形、邊長等比例」求得輸出值。
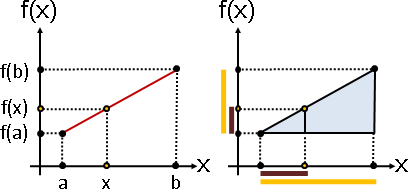
x - a
f(x) = ——————— ⋅ (f(b) - f(a)) + f(a)
b - a
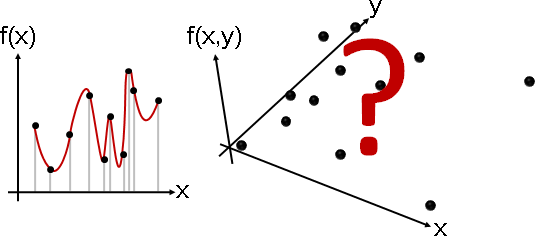
quadratic interpolation
「二次內插」。內插函數是許多個二次多項式。
f = Interpolation[{{20,85},{40,30},{65,70},{90,120},{105,40},{115,95},{130,45},{140,150},{145,125},{175,115}}, InterpolationOrder->2]; g1 = Plot[f[x], {x, 0, 200}, PlotRange -> {-50, 200}]; g2 = ListPlot[{{20,85},{40,30},{65,70},{90,120},{105,40},{115,95},{130,45},{140,150},{145,125},{175,115}}]; Show[g1,g2]
輸入值相鄰的函數點,以二次多項式函數連接。令函數銜接之處(函數點)一次導數相同。
化作一次方程組,求得內插函數:
方程式共四類:一、每一段二次多項式函數,代入左端點。二、代入右端點。三、每一對相鄰的二次多項式函數的一次導數,代入銜接之處,必須相等。四、追加一道方程式,以求得唯一解。令第一個二次多項式函數的二次導數是零。
二次內插效果差,無人使用。
cubic interpolation
「三次內插」。內插函數是許多個三次多項式。

f = Interpolation[{{20,85},{40,30},{65,70},{90,120},{105,40},{115,95},{130,45},{140,150},{145,125},{175,115}}]; Plot[f[x], {x, 0, 200}, PlotRange -> {-50, 200}]
輸入值相鄰的函數點,以三次多項式函數連接。令函數銜接之處(函數點)一次導數相同、二次導數相同。
必須自訂每個函數點的一次導數是多少。例如自身、左邊,兩個函數點的斜率。
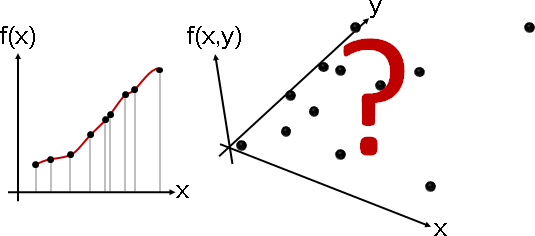
monotone cubic interpolation
「單調三次內插」。函數點嚴格遞增(減),內插函數是許多個嚴格遞增(減)三次多項式。其他地方與三次內插相同。
p = {{20,85},{40,30},{65,70},{90,120},{105,40},{115,95},{130,45},{140,150},{145,125},{175,115}}; q = Transpose[{ p[[All,1]] , Sort[p[[All,2]]] }] f = Interpolation[q]; Plot[f[x], {x, 0, 200}, PlotRange -> {-50, 200}]
有時候我們希望內插函數擁有反函數。又要多項式函數、又要反函數,那就只能是嚴格遞增(減)函數了。此時「單調一次內插」、「單調三次內插」能派上用場。
spline interpolation
兩個相鄰函數點,取附近k個函數點,求得多項式內插函數,然後截取兩個相鄰函數點之間的那一段。
窮舉相鄰函數點,銜接成內插函數。
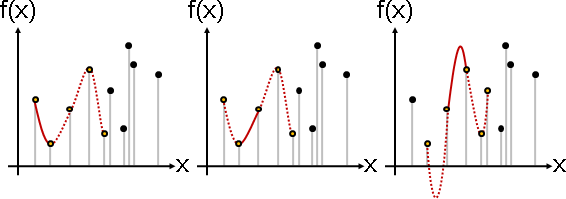
Catmull–Rom spline interpolation
兩個相鄰函數點,取附近4個函數點,以Neville interpolation求得多項式內插函數,但是遞推最後一步改成中央兩點。其餘同前。
效果是緩和曲線。副作用是4個函數點只穿過中央兩點,導致左右邊界各漏失一段內插函數。解法是在邊界外面補充函數點。
等價於cubic interpolation:令一次導數是左右兩點的斜率。
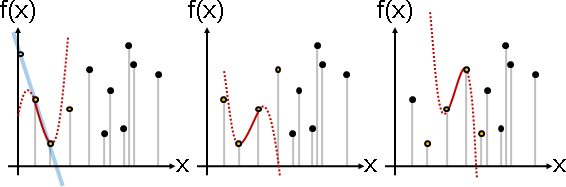
bilinear interpolation
二元函數,輸入值形成格點,一次內插只有唯一一種結果,稱作「雙一次內插」。
每個格子,上方兩點做一次內插、下方兩點做一次內插,得到兩點再做一次內插。
改成左方兩點、右方兩點,結果仍相同。
q = {{{1,1},0},{{1,2},0},{{1,3},4},{{1,4},1},{{1,5},1},{{2,1},4},{{2,2},3},{{2,3},4},{{2,4},1},{{2,5},0},{{3,1},1},{{3,2},0},{{3,3},0},{{3,4},4},{{3,5},3},{{4,1},2},{{4,2},3},{{4,3},4},{{4,4},0},{{4,5},1},{{5,1},3},{{5,2},3},{{5,3},0},{{5,4},1},{{5,5},2}}
n = 5; p1 = Tuples[Range[n], 2]; p2 = RandomInteger[4,n*n]; q = Transpose[{p1,p2}]; f = Interpolation[q, InterpolationOrder->1]; g1 = Plot3D[f[x,y], {x, 1, n}, {y, 1, n}, PlotRange -> {0, 7}, Boxed -> False, Axes -> False, Mesh -> (n-2), PlotPoints -> 50, ColorFunction -> (ColorData["CherryTones"][Rescale[#3, {-4, 4}]] &)]; q2 = Transpose[{p1[[All,1]],p1[[All,2]],p2}]; g2 = Graphics3D[{Black, Ball[q2, 0.1]}]; Show[g1,g2]
bicubic interpolation
二元函數,輸入值形成格點,三次內插只有唯一一種結果,稱作「雙三次內插」。
每個格子,上方兩點做三次內插、下方兩點做三次內插,得到兩點再做三次內插。
改成左方兩點、右方兩點,結果仍相同。
basis interpolation
radial basis function interpolation
RBF是圓對稱的函數。等高線是同心圓。名稱莫名其妙。
實際應用當中,大家視之為「向四周釋放力場的函數」,內高外低。函數造型任君挑選,例如Gaussian function。
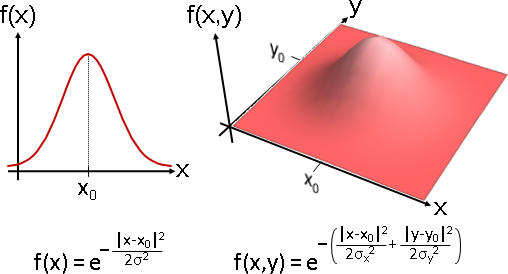
Plot3D[PDF[MultinormalDistribution[{0, 0}, {{1, 0}, {0, 1}}], {x, y}], {x, -3, 3}, {y, -3, 3}, PlotRange -> {0,0.18}, Boxed -> False, Axes -> False, Mesh -> None, ColorFunction -> (ColorData["CherryTones"][Rescale[#3, {-2, 2}]] &) ]
函數點的RBF的加權總和,作為內插函數。
實際應用當中,挑選一種力場,明定高矮胖瘦。函數點釋放力場,力場乘上權重,調整強弱。疊加力場,得到內插函數。
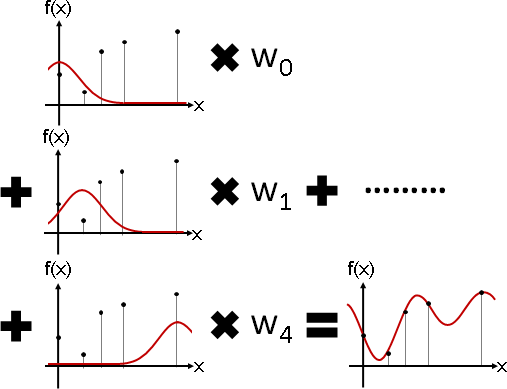
w0 = Exp[- (x - 0) ^ 2 / 8]; w1 = Exp[- (x - 2) ^ 2 / 8]; w2 = Exp[- (x - 3) ^ 2 / 8]; w3 = Exp[- (x - 5) ^ 2 / 8]; w4 = Exp[- (x - 9) ^ 2 / 8]; f = 149.646 * w0 - 391.202 * w1 + 376.984 * w2 - 62.8542 * w3 + 71.1682 * w4; Plot[f, {x, -1, 10}]
為了穿過所有函數點,需要解方程組,求得權重。
之所以採用加權總和,正是因為一次方程組容易求解。
Φ(d) = exp(d² / 2σ²) σ is constant ⎡ Φ(‖x₀-x₀‖) Φ(‖x₀-x₁‖) .. Φ(‖x₀-xɴ₋₁‖) ⎤ ⎡ w₀ ⎤ ⎡ y₀ ⎤ ⎢ Φ(‖x₁-x₀‖) Φ(‖x₁-x₁‖) .. Φ(‖x₁-xɴ₋₁‖) ⎥ ⎢ w₁ ⎥ ⎢ y₁ ⎥ ⎢ : : : ⎥ ⎢ : ⎥ = ⎢ : ⎥ ⎢ : : : ⎥ ⎢ : ⎥ ⎢ : ⎥ ⎣ Φ(‖xɴ₋₁-x₀‖) Φ(‖xɴ₋₁-x₁‖) .. Φ(‖xɴ₋₁-xɴ₋₁‖) ⎦ ⎣ wɴ₋₁ ⎦ ⎣ yɴ₋₁ ⎦
B-spline interpolation
Neville interpolation是常數函數(高度是yᵢ)的一次內插。
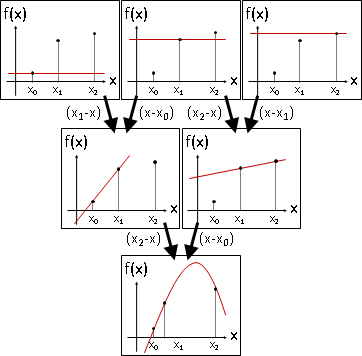
B-spline是矩形函數(高度是1)的反一次內插(權重互換)。
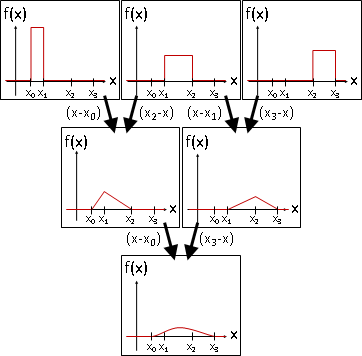
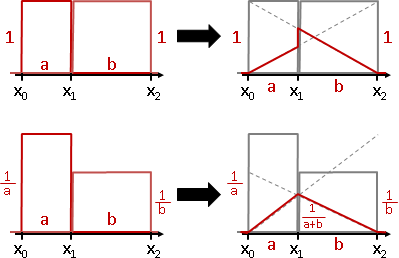
為了形成山丘:首先高度除以寬度,才做反一次內插;最後高度乘以總寬度,高度還原為1。
函數點的B-spline的加權總和,作為內插函數。
為了穿過所有函數點,需要解方程組,求得權重。
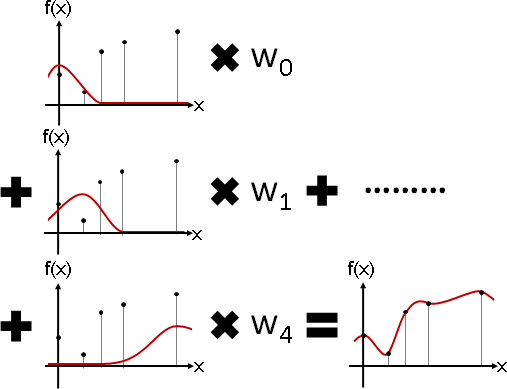
B-spline是許多個多項式,每遞推一層就升高一次方。遞推層數越多,曲線越平緩。大家習慣遞推三層、得到三次多項式,曲線不會太過平緩,而山峰也恰好對齊函數點。
如同Catmull–Rom spline,需要在邊界外面補充函數點。
inverse distance weighting interpolation
(Shepard interpolation)
距離倒數函數,顧名思義。若想高䠷纖瘦,就取k次方。
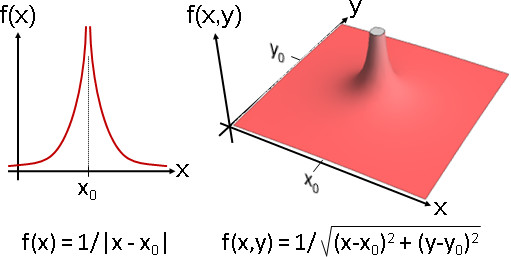
Plot3D[1/Norm[{x,y}], {x, -1, 1}, {y, -1, 1}, PlotRange -> {0,15}, Boxed -> False, Axes -> False, Mesh -> None, ColorFunction -> (ColorData["CherryTones"][Rescale[#3, {-2, 2}]] &) ]
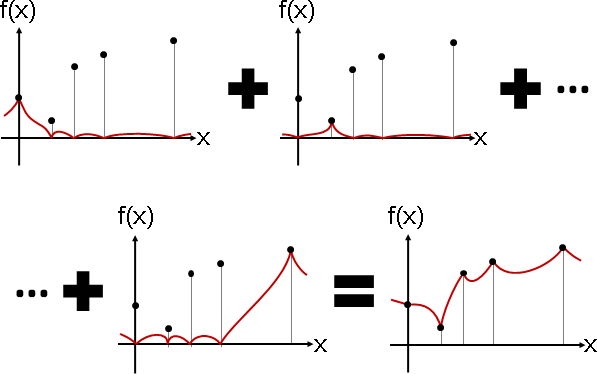
函數點的距離倒數函數的加權平均數,作為內插函數。
為了穿過所有函數點,令各個距離倒數函數,穿過自己的函數點,不穿過其餘的函數點,仿效Lagrange interpolation。
手法:一、各個距離倒數函數除以其總和。二、權重是輸出值。
wᵢ(x) = (1 / ‖x - xᵢ‖)ᵏ for i = 0...N-1 (k is constant)
w (x) = w₀(x) + w₁(x) + ...
w₀(x) w₁(x) w₀(x) y₀ + w₁(x) y₁ + ...
f(x) = ————— y₀ + ————— y₁ + ... = ———————————————————————————
w (x) w (x) w₀(x) + w₁(x) + ...
w0 = 1/Abs[x]; w1 = 1/Abs[x-2]; w2 = 1/Abs[x-3]; w3 = 1/Abs[x-5]; w4 = 1/Abs[x-9]; w = w0 + w1 + w2 + w3 + w4; f = w0 * 32 + w1 * 12 + w2 * 43 + w3 * 55 + w4 * 66; Plot[f/w, {x, -1, 10}]
再介紹另外一種解讀方式,稍微艱澀。
函數點的常數函數的加權平均數,作為內插函數。
權重不是數值,而是函數──根據內插點位置,決定權重多寡。此處使用距離倒數函數,也可以換成別的函數。
為了穿過所有函數點,權重必須滿足兩個條件:
一、無論內插點在何處,權重總和必須是1。輕鬆解套方式:各權重除以權重總和。
二、當內插點位於函數點,該常數函數的權重必須是1,其餘必須是0。輕鬆解套方式:權重趨近無限大。
Fᵢ(x) = yᵢ for i = 0...N-1
wᵢ(x) = (1 / ‖x - xᵢ‖)ᵏ for i = 0...N-1 (k is constant)
w₀(x) F₀(x) + w₁(x) F₁(x) + ...
f(x) = —————————————————————————————————
w₀(x) + w₁(x) + ...