State
道生之，德畜之，物形之，勢成之。《老子》
State
一件事物，以宏觀、全知的觀點望去，當前的模樣稱作「狀態」。比方說：影片拍攝著一臺行駛中的車輛，底片的一格畫面，就是一個狀態。
狀態可以是一盤棋的局面，也可以是今天下午五點整的車輛分布情況。狀態與狀態之間，可以是離散的（棋盤局面），也可以是連續的（車潮）。
Transition
每一個狀態都可以經過特定動作，改變現有狀態、轉移到下一個狀態。例如象棋，我們可以移動一顆棋子到其他空地、移動一顆棋子收拾對手的棋子。例如車潮，每一輛車可以踩油門、煞車、轉彎。這樣的動作叫做「轉移」。
State Space Tree
State Space Graph
「狀態空間圖」。所有狀態互相轉移，形成了圖論的有向圖。狀態就是點，轉移就是邊，轉移成本就是邊的權重。
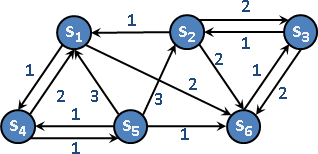
State Space Tree
「狀態空間樹」。選定一個狀態，衍生各式各樣的狀態，形成一棵樹。狀態空間樹無窮無盡。狀態可能重複出現、四處散布。
用途：從「起始狀態」到其他狀態，求得轉移過程。
用途：從「起始狀態」到「目標狀態」，求得轉移過程。
搜尋順序
如何迅速找到目標狀態呢？
狀態空間樹無窮無盡，只好一邊建立、一邊搜尋。乍看離目標狀態比較近的狀態，優先搜尋。
如何衡量目標狀態的遠近呢？
已經搜尋的狀態，累計轉移成本；尚未搜尋的狀態，估計轉移成本。成本較低的狀態，優先搜尋。
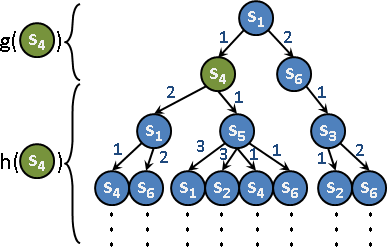
cost function g(x)：起始狀態到當前狀態x，真正的轉移成本。c(s⤳x)。
heuristic function h(x)：當前狀態x到目標狀態，預估的轉移成本。c̃(x⤳t)。
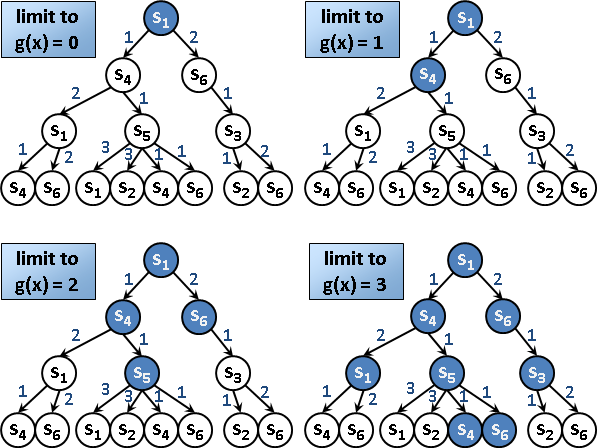
g(x)由小到大搜尋：首次遇到的目標狀態，就是g(x)最小的目標狀態。
h(x)由小到大搜尋：首次遇到的目標狀態，不一定就是g(x)最小的目標狀態。因為h(x)不準確。
g(x)+h(x)由小到大搜尋：首次遇到的目標狀態，不一定就是g(x)最小的目標狀態。因為h(x)不準確。
admissible heuristic：h(x)小於等於真正的轉移成本。h(x) ≤ c(x⤳t)。 consistent heuristic：h(x)滿足單調性。h(x) ≤ c(x⤳y) + h(y)。
g(x)+h(x)由小到大搜尋，並且h(x)小於等於真正的轉移成本（不高估）：首次遇到的目標狀態，就是g(x)最小的目標狀態。當h(x)預估精準，得以迅速走往目標狀態，不會四處閒逛。
g(x)+h(x)由小到大搜尋，並且h(x)滿足單調性：首次遇到的各種狀態，都是g(x)最小的狀態。也就是說，每種狀態只需拜訪一次。時間複雜度O(NDK)，其中狀態數量為N，分枝數量為D，轉移需時O(K)。
UVa 260 298 314 321 429 571 589 704 985 10047 10603 10653 10682 10923 10103 10704 10067
UVa 529 851 10073 10422 10798 11163 11376 10314
搜尋演算法
圖論的遍歷演算法，進行改良，建立暨搜尋狀態空間樹。
Breadth-first Search（BFS） 忽視g(x)、h(x)，優先建立離起始狀態最近的狀態。 適用於轉移成本是固定值。 Depth-first Search（DFS） 忽視g(x)、h(x)，優先建立離起始狀態最遠的狀態。 適用於轉移成本是固定值。 Depth-limited Search（DLS）/ 過去稱作 Depth-first Branch-and-Bound（DFBnB） DFS的改良版本。限制建立的深度（或成本），當深度（或成本）太深就不再往下分枝衍生。 Iterative Deepening DFS（IDS） DLS的改良版本。反覆使用DLS，並逐次放寬深度限制。 若每次放寬的量極少時，可達到類似於BFS的功能。 Uniform-cost Search（UCS） g(x)由小到大建立。以BFS實作。 Iterative Lengthening Search（ILS） g(x)由小到大建立。以IDS實作，逐次放寬g(x)的限制。 若每次放寬的量極少時，可達到類似UCS的功能。 Best-first Search h(x)由小到大建立。以BFS實作。 Recursive Best-first Search（RBFS） h(x)由小到大建立。以IDS實作，逐次放寬h(x)的限制。 若每次放寬的量極少時，可達到類似Best-first Search的功能。 A* Search（A*） g(x)+h(x)由小到大建立。以BFS實作。 Iterative Deepening A* Search（IDA*） g(x)+h(x)由小到大建立。以IDS實作，逐次放寬g(x)+h(x)的限制。 若每次放寬的量極少時，可達到類似A*的功能。 Memory-bounded A* Search（MA*） / Simplified Memory-bounded A* Search（SMA*） 限制記憶體用量的A*。當queue全滿時，就從中刪除g(x)+h(x)最大的狀態。
名稱天花亂墜，令人眼花撩亂。其實最關鍵的地方，在於搜尋順序、搜尋演算法的差別。
搜尋順序：g(x)、h(x)、g(x)+h(x) 搜尋演算法：BFS、IDS
搜尋順序，採用g(x)或者g(x)+h(x)，以正確求得最佳成本。
搜尋演算法，BFS系列，效率較差；IDS系列，效率較好。
假設狀態空間樹剛好是一棵二元樹，而目標狀態位於第N層。BFS搜尋的狀態數目是(1+2+4+8+...+2ᴺ)，IDS搜尋的狀態數目是1 + (1+2) + (1+2+4) + ... + (1+2+4+8+...+2ᴺ)，大約是前者的兩倍。如果狀態空間樹是K元樹，則大約是前者的K倍。
儘管BFS搜尋的狀態數目比起IDS少了許多倍，然而BFS必須維護priority queue，還得indexing，因此BFS的執行時間通常比起IDS長上許多，而且記憶體用量也大上許多。
IDS逐步放寬g(x)或者g(x)+h(x)的限制，不必比較成本大小。這使得IDS不需要priority queue。
搜尋策略
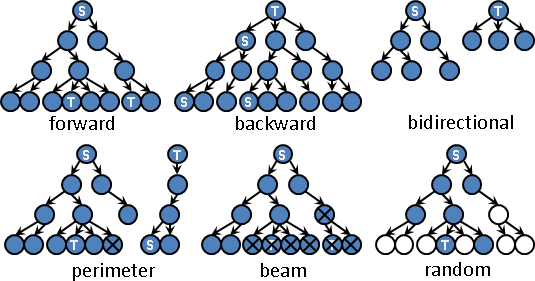
forward search：正向搜尋。起始狀態建立狀態空間樹，從中搜尋目標狀態。
backward search：反向搜尋。目標狀態建立狀態空間樹，從中搜尋起始狀態。
bidirectional search：雙向搜尋。起始狀態、目標狀態分別建立狀態空間樹，搜尋共同狀態。實作時，通常是輪流衍生。狀態空間樹輪流增加一層，直到兩邊出現共同狀態。
perimeter search：周界搜尋。起始狀態建立狀態空間樹，儲存所有狀態，直到記憶體幾乎用光。然後目標狀態建立狀態空間樹，直到出現儲存過的狀態。實作時，通常起始狀態採用BFS，目標狀態採用DFS、IDS、IDA*等節省記憶體的搜尋演算法。
beam search：柱狀搜尋。限制狀態空間樹每一層的狀態數目。當某一層抵達上限後，該層後來產生的狀態皆捨棄。
random search：隨機搜尋。隨機決定衍生哪些狀態。
heuristic search：啟發搜尋。按照經驗法則，決定衍生哪些狀態。例如台灣的交通網，西部比東部密集。從基隆到屏東，首先去台北，而不是去宜蘭──根據交通網密度，台北可能更快到達屏東。
ICPC 5098
搜尋技巧
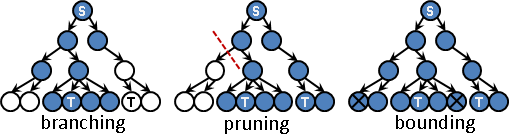
branching：視情況衍生分枝。逐漸增加成本下限，逼近正確答案；一旦超過成本上限，立即停止分枝。
pruning：參照問題本身的特殊限制，裁剪狀態空間樹，避開冗餘子樹。好處是減少搜尋時間。
bounding：搜尋時，隨時檢查成本。成本太壞，就不再往深處搜尋；成本足夠好，也不必往深處搜尋。好處是減少搜尋時間。
tie-breaking：搜尋時，當g(x)或者g(x)+h(x)平手，則比較h(x)，優先搜尋h(x)較小的狀態，以便提早抵達目標狀態。
memoization：記錄所有遭遇到的狀態，避免狀態空間樹重複衍生相同狀態。當記憶體不足時，也可以只記錄一部分的狀態。
indexing：狀態編號，方便memoization。當記憶體不足時，indexing可以改為hashing。
UVa 233 10536 10941 690 ICPC 6010
應用：Pathfinding
即時戰略遊戲，用滑鼠點選角色的目的地，角色自動繞過障礙物，找到最短路徑。
應用：3 Jugs Problem
3 Jugs Problem
手邊有三個裝水的容器，容量由大到小分別是X公升、Y公升、Z公升，都沒有刻度。其中X公升的容器已經裝滿水了。
問題：如何在這三個容器之中，將水倒來倒去，使得其中一個容器恰有W公升的水？
資料結構
使用三個變數記錄容器的容量。再使用三個變數記錄容器中的水量。
三個容器的裝水情況，視作一個狀態。
起始狀態：一個滿容器、兩個空容器
一開始只有X公升的容器裝滿水，另外兩個容器沒有裝水。
目標狀態：其中一個容器裝了W公升的水量
狀態轉移：把A容器的水倒入到B容器中
兩種情形：
一、A水量不夠、B剩餘容量太多，倒不滿B，A沒有剩水。
二、A水量太多、B剩餘容量不夠，B被倒滿，A還有剩水。
不能只倒一些！原因是容器沒有刻度，無法精準的控制水量，無法保證最終結果正是W公升。
成本
倒一次水，算一個步驟。成本定為1。
空間複雜度
為了避免同樣的狀態重複出現、重複衍生，只好記錄所有遭遇過的狀態。三個容器的水量範圍是0⋯X公升、0⋯Y公升、0⋯Z公升，所有狀態總共(X+1)(Y+1)(Z+1)個。空間複雜度O(XYZ)。
時間複雜度
倒水方式總共3⋅2種。也就是說，一個狀態衍生O(3⋅2)個狀態。時間複雜度O(XYZ ⋅ 3⋅2) = O(XYZ)。
搜尋演算法：BFS
判斷起始狀態是否能夠轉移到目標狀態。
加碼求得起始狀態到目標狀態的轉移過程。
UVa 10603
應用：8 Puzzle Problem
8 Puzzle Problem
3×3方塊拼圖，缺了一格。上下左右推動方塊，讓它排列整齊。
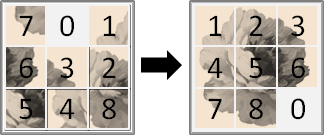
處理這個問題時，每塊方塊標上數字編號，會更清楚一些。
4×4叫做15 Puzzle。N×M叫做Sliding Puzzle。
檢查不合理的盤面：Permutation Inversion
當一個盤面的inversion的個數是偶數的時候，表示該盤面可以從排列整齊的狀態，經過一連串推動而得；如果個數是奇數，則表示該盤面不合理、不可能存在。另外還要考慮空格位於哪一列。
heuristic function
這裡提供兩種不高估的方法，不高估的理由都很明顯：
1. 不在正確位置上的方塊個數。 2. 每個方塊與其正確位置的 taxicab distance 的總和。
搜尋演算法：IDA*
UVa 652 10181 10085
應用：Rat in a Maze
老鼠走迷宮
老鼠很聰明，進入死胡同就會馬上回頭，不會傻傻的一直進入同一個死胡同。老鼠每一次重跑，都會越來越快。老鼠也會選擇看起來離乳酪比較近的路線。
一開始就已經背熟地圖，隨意找出一條路線。
由於原本的線條牆壁迷宮難以實作，不太適合初學者，所以這裡採用方塊牆壁迷宮，走一格當作是一步。
#########
#
_________ # ### ###
__ __| # # #
| |____ | ---> # ##### #
| __ |_| # # #
|____|____ # ### ###
# #
#########
前面的程式碼只求出了老鼠的行走距離。想要印出老鼠走過的路線，必須新增一條陣列，記錄老鼠的軌跡。
一開始就已經背熟地圖，找出最佳路線。
使用BFS搜尋狀態空間樹，先遇到的目標狀態，會是成本最小的目標狀態。
搜尋過的狀態都會存放在queue裡面。要印出最佳路徑，可以在節點裡面新增加一個變數，記錄狀態的來源。
一開始不知道地圖，第一次走，隨意找出一條路線。
以下介紹兩種走迷宮的智慧：
有一種走迷宮的方式，叫做右手原則。當迷宮的入口、出口都在外牆，而且迷宮裡面沒有環狀路線，此時只要用右手一直摸著牆走，一定可以走出迷宮。右手原則其實就是一種DFS。各位可以仔細觀察影片，說不定老鼠真的懂右手原則喔！
在迷宮上隨意框一塊區域，如果只剩一個以下開口，則不必走進去，因為一定出不來；如果仍有兩個以上開口，則可以考慮走進去，有可能走得出來，也可能走不出來。如果老鼠一開始知道迷宮大小，也知道自己行走的方向、走了幾步路，如此老鼠隨時可以推敲出自己是不是走入了一個沒有出口的區域。
各位應該也能設計出許多種走迷宮的智慧。如果有興趣，可以上網搜尋一些老鼠走迷宮的影片來研究。
一開始不知道地圖，再走幾次，逐次找出更佳路線。
如果老鼠記憶力很強，記得走過的地點（甚至是路），我們在實作時，就可以運用memoization，把搜尋過程中遭遇到的地點統統記錄起來。老鼠的記憶力，就變成了電腦的記憶體。
老鼠行動時，會有一定機率去探索未知的區域，並且會將探索結果記在腦海中。然而現實中，老鼠的記憶力有限，也就是電腦的記憶體有限，不能記得所有地點。想要模擬老鼠的記憶力，可以限制電腦的記憶體用量，當記憶體用罄時，就忘掉一些地點。例如queue、hash table都是不錯的選擇。
製造迷宮（Wilson's Algorithm）
延伸閱讀：步伐儲存方式
西洋棋騎士。
UVa 10426 10463 10477 633
方塊滾動。
UVa 10021
Game Tree
Game Tree
「遊戲樹」。兩人對陣，輪流動作，形成的狀態空間樹。
用途：從「起始狀態」到「勝負已分狀態」，求得轉移過程。
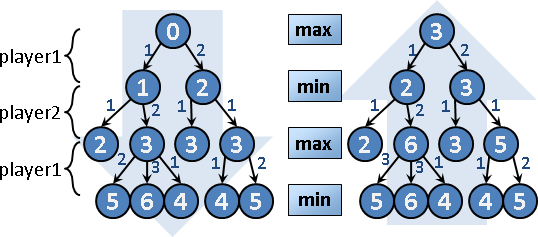
遊戲樹的理念：
一、先手嘗試勝利。即便不能勝利，也要盡量拖延，讓後手難以勝利。後手亦然。
二、先手從眾多動作當中，一律選擇最佳動作。後手亦然。
遊戲樹的設計思路：
一、互相拔河。先手志於往右，後手志於往左。
二、改成數值。先手志於高分，後手志於低分。
三、先手從下層節點分數之中取最大值，後手取最小值。
遊戲樹比狀態空間樹還要多算一項東西：
一、計算每個節點的成本。由根往葉，累計成本。
二、計算每個節點的分數。由葉往根，取max()或min()。
往下遍歷到樹葉（勝負已定），得到樹葉的成本；往上回溯到樹根（開局狀態），得到樹根的分數。
UVa 682 10111 10838 ICPC 4451
分數類型
一、最高分數：先手取max()，先手在max層。
通常後手也想得高分，然而後手取min()無法得高分。解法：正分數為先手贏，負分數為先手輸。負分數變號，得到後手分數。
二、最少步數：先手取min()，先手在min層。
有時先手贏不了、先手拖延步數，此時取max()而非min()。解法：當先手贏不了，把步數設定成由很大的數字N開始減少。N步是後手零步贏，N-1步是後手一步贏。先手只需取min()，先取到贏的步數，取不到時才會取到拖延步數。
搜尋演算法
Minimax Tree Search DFS搜尋。一般來說。 Monte–Carlo Tree Search 隨機搜尋。難以求得精確分數，於是分數改成勝率。
搜尋技巧
Minimax Tree Search：
Negamax 取max()、取min()，一律改成取max()。 取min()時，分數先變號、取max()、再還原變號。 效果是精簡程式碼。 α–β Pruning 搜尋時，當前分數已經超出範圍，立即結束搜尋、往樹根回溯。 搜尋演算法必須採用DFS，才能即時更新範圍。 Null Window 猜答案。假設分數為a或a+1，將範圍設定成[a,a+1]，實施搜尋。 效果宛如branching。如果逐步放寬範圍，效果宛如IDS。 Scout 先猜一次答案，如果沒有超出範圍，才正式搜尋。 效果宛如pruning。 MTD(f) 不斷猜答案，不斷縮小範圍。 效果宛如二元搜尋。
Monte–Carlo Tree Search：
Upper Confidence Bound (UCB) 優先搜尋勝機較高的節點，勝機是特定經驗公式。
搜尋技巧：α-β Pruning
必須採用DFS。回溯時，即時更新節點的分數範圍。
α pruning：假設本層max層，上層min層。本層分數大於等於上層分數，喪失意義，立即回溯。實作時，上層分數α作為函式參數。
β pruning：假設本層max層，上上層max層。本層分數大於上上層分數，才有意義。本層分數範圍，左端的初始值設定為上上層分數。β pruning單獨使用沒有效果，配合α pruning才有效果。實作時，上上層分數β作為函式參數。
max層的分數範圍是[β,α]，min層是[α,β]。方便起見，教科書一律寫成[α,β]。因此教科書的描述跟本文稍有不同。
具備連鎖效果，不必特地處理本層與上上上層。
應用：Tic-tac-toe
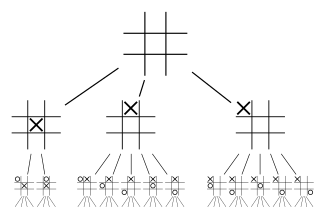
Markov Chain
一切諸國土，皆隨業力生，汝等應觀察，轉變相如是。《華嚴經》
Markov Chain（Discrete Markov Process）
許多個狀態，每個狀態都可以轉移到其他狀態，轉移機率的總和都是1。轉移機率習慣寫成一個矩陣，稱作「轉移矩陣Transition Matrix」、「隨機矩陣Stochastic Matrix」。
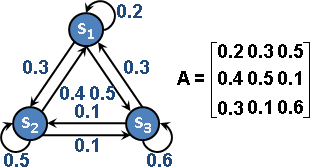
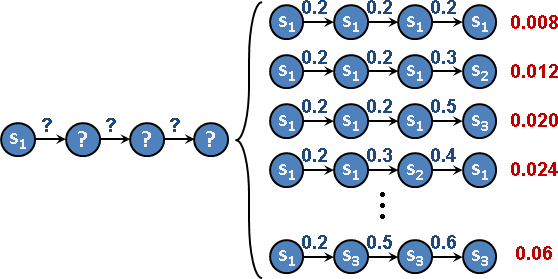
選定一個狀態作為起點，不斷移動（不斷轉移狀態、狀態不斷變化），走出一條路線。考慮所有可能的路線，每一條路線都可以明確計算其機率。將所有路線，朦朧地幻想成一條路線，步步充滿隨機，這條路線叫做「馬可夫鏈」。
Markov Chain可以看成圖論的有向圖：狀態是點，轉移是邊，機率是邊的權重，轉移矩陣是資料結構Adjacency Matrix。
Markov Chain的主要功用是預測未來發展。體積微小、性質穩定的東西（例如空氣分子、細胞），適合使用Markov Chain模擬未來發展（例如氣體擴散、細胞繁殖）。Markov Chain是物理模擬、化學模擬領域的重要工具。
UVa 10828 11021 11762 12730 11680
相關術語
reducibility：狀態x到y，有路可通（機率大於零）。
periodicity：狀態x到x，找出環的長度。
recurrent：狀態x出發，所有路線都走回x，無法擺脫輪迴。
走n步抵達什麼狀態？
藉由矩陣n次方、轉置、求值，得到每個狀態的抵達機率。
一個狀態的抵達機率：來源狀態們各自乘上轉移機率，再加總。
走1步：轉移矩陣的1次方，轉置之後，乘以初始向量。 走n步：轉移矩陣的n次方，轉置之後，乘以初始向量。 走∞步：轉移矩陣的∞次方，轉置之後，乘以初始向量。圖論Transitive Closure。
向量：每個狀態的抵達機率。 初始向量：起點狀態的抵達機率是1，其餘狀態的抵達機率是0。
走∞步抵達什麼狀態？
藉由矩陣的特徵向量、特徵值，得到每個狀態的抵達機率。
數學家已經證明：
一、eigenvalue一定包含1。 二、所有的eigenvalue，絕對值均小於等於1。
結局可能是：
一、只有一個1，其他均小於1：收斂至1的eigenvector的方向上面。 二、有許多個1：收斂至這些eigenvector構成的區域裡面。 三、有-1：狀態不斷循環。 四、有虛數、其長度為1：狀態不斷循環。
走∞步，可能匯合到某些狀態，也可能循環繞圈。
倘若這個世界的時間線是Markov Chain，那麼這個世界的未來，也許同歸於一，也許不斷輪迴。
走∞步抵達什麼狀態？
當轉移矩陣是對稱矩陣，藉由Metropolis Sampling，得到每個狀態的抵達機率。
關鍵字stationary distribution、steady state distribution、equilibrium distribution。
應用：Animation State Machine
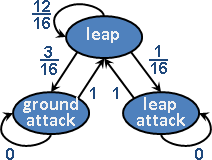
遊戲動畫、遊戲AI、遊戲平衡的經典工具！
這裡提供的Markov Chain只是推測，應該是錯的。
應用：Random Walk on 3x3 Grid
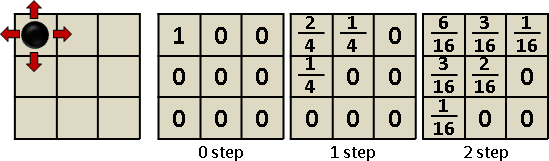
一個3x3的方格棋盤，左上角放著一個棋子。棋子可以上下左右移動一格，機率各是1/4。如果棋子出界，那麼棋子歸回原位。
棋子走零步，停於左上的機率為1，其餘格子為0。
棋子走一步，停於左上的機率為2/4，上、左的機率各為1/4，其餘為0。
棋子走兩步，停於左上的機率為6/16，上、左的機率各為3/16，右上、左下的機率各為1/16，中央為2/16，其餘為0。
棋子走n步呢？首先畫出狀態空間圖。
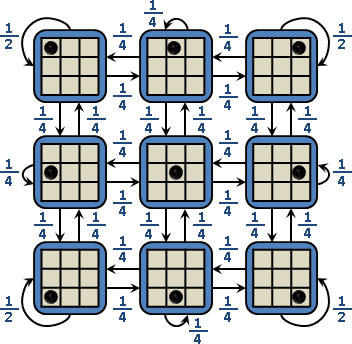
狀態編號。
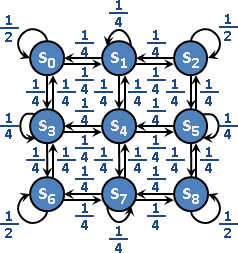
轉移矩陣A、初始向量x₀。
初始狀態是棋子位於左上角。初始狀態是狀態第0號，其出現機率是1。初始向量的第0個元素是1、其餘元素為0。
⎡ 2 ⎤ ⎡ 2 1 0 1 0 0 0 0 0 ] ⎡ 1 ⎤
⎢ 1 ⎥ ⎢ 1 1 1 0 1 0 0 0 0 ] ⎢ 0 ⎥
⎢ 0 ⎥ ⎢ 0 1 2 0 0 1 0 0 0 ] ⎢ 0 ⎥
1 ⎢ 1 ⎥ 1 ⎢ 1 0 0 1 1 0 1 0 0 ] ⎢ 0 ⎥
——— ⎢ 0 ⎥ = ——— ⎢ 0 1 0 1 0 1 0 1 0 ] ⎢ 0 ⎥
4 ⎢ 0 ⎥ 4 ⎢ 0 0 1 0 1 1 0 0 1 ] ⎢ 0 ⎥
⎢ 0 ⎥ ⎢ 0 0 0 1 0 0 2 1 0 ] ⎢ 0 ⎥
⎢ 0 ⎥ ⎢ 0 0 0 0 1 0 1 1 1 ] ⎢ 0 ⎥
⎣ 0 ⎦ ⎣ 0 0 0 0 0 1 0 1 2 ] ⎣ 0 ⎦
^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^
x₁ Aᵀ x₀
走n步，即是轉移矩陣的n次方，轉置之後，乘以初始向量。
發揮想像力，應用非常廣：迷路回不了家的機率、人類經濟活動與最終財富分配、世界終焉之時萬物將何去何從、……。
應用：PageRank
Markov Network
Markov Network（Discrete Markov Random Field）
「馬可夫網路」。馬可夫鏈從有向路徑推廣成無向圖。
馬可夫鏈，只有先前狀態會影響現況。馬可夫網路，只有鄰近狀態會影響現況。
馬可夫鏈是馬可夫隨機過程離散化，馬可夫網路是馬可夫隨機場離散化。
n個事件： 天氣(晴/陰/雨)、心情(好/普/糟)、行為(洗澡/睡覺)、成績(0...100)、...。 上古統計學：問卷收集大量案例（樣本），得到n維的marginal distribution。 機率圖模型：一個函數，輸入是一堆事件（的分布），輸出是另一堆事件（的分布）。 例如 輸入：天氣、心情。 輸出：行為的機率分布。 現在要找迴歸函數：給定一堆樣本，請找到最符合樣本的函數。 然而很難找：建圖方式百百種，排列組合超多。 輸入/輸出/中繼節點不知道要安排那些事件。 解法：憑主觀直覺建圖，最後再把事件一一指派到節點。例如Boltzmann Machine。 解法：憑經驗法則建圖，最後再套用一些規則以簡化圖。例如Chow–Liu Tree。
Hammersley–Clifford Theorem: prod phi(cliques) phi(.) > 0
Bayes Network（Bayesian Network）
「貝葉斯網路」。無向圖改成有向圖。