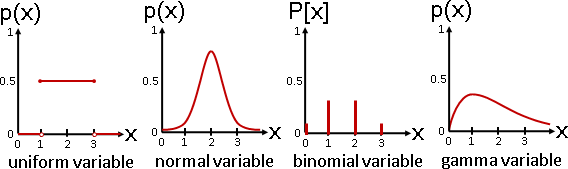
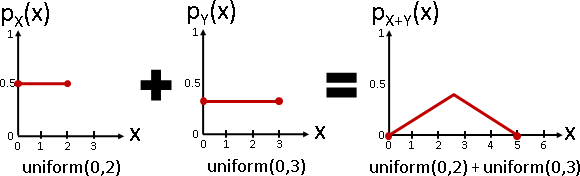
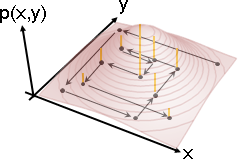
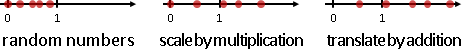multivariate random variable與joint distribution
我們可以個別調整每一種數組的出現程度高低。數學家命名為「多變量隨機變數」。理想的名稱應是「浮動數組」。
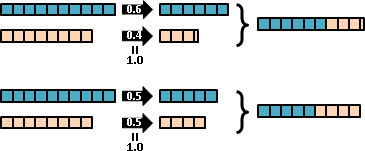
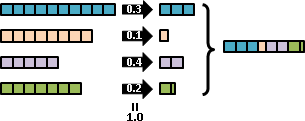
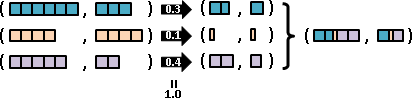
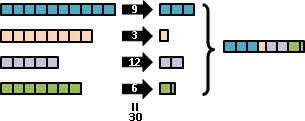
至於「每一種數組的出現程度高低」的函數,數學家命名為「聯合分布」。之前介紹了許多經典的分布,通通可以推廣成聯合分布。
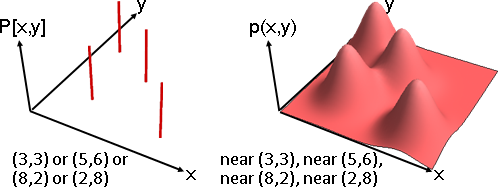
l = {Line[{{3,3,1},{3,3,0}}], Line[{{5,6,1},{5,6,0}}], Line[{{8,2,1},{8,2,0}}], Line[{{2,8,1},{2,8,0}}]};
g = Show[ListPointPlot3D[{0,0,0}, Boxed -> False, Axes -> False, PlotRange -> {{0,10},{0,10}}], Graphics3D[{Thickness[0.01], CapForm["Butt"], Red, l}]]
img = ImageResize[Rasterize[g, "Image", ImageResolution -> 72*3], Scaled[1/3]];
ImageCrop[RemoveBackground[img, {{{0, 0}}, 0.1}]]
F[x_, y_] := PDF[MultinormalDistribution[{3, 3}, {{1, 0}, {0, 1}}], {x, y}] +
PDF[MultinormalDistribution[{5, 6}, {{1, 0}, {0, 1}}], {x, y}] +
PDF[MultinormalDistribution[{8, 2}, {{1, 0}, {0, 1}}], {x, y}] +
PDF[MultinormalDistribution[{2, 8}, {{1, 0}, {0, 1}}], {x, y}];
Show[
Plot3D[F[x,y], {x, 0, 10}, {y, 0, 10}, PlotRange -> All, Boxed -> False, Mesh -> None, Axes -> False, PlotPoints -> 50, ColorFunction -> (ColorData["CherryTones"][Rescale[#3, {-4, 4}]] &)],
ParametricPlot3D[{x, 2, F[x,2]}, {x, 0, 10}, PlotStyle -> Red]
]
Plot[F[x,2], {x, 0, 10}, PlotRange -> All, PlotStyle -> Red, Axes -> False]
Show[
Plot3D[F[x,y], {x, 0, 10}, {y, 0, 10}, PlotRange -> All, Boxed -> False, Mesh -> None, Axes -> False, PlotPoints -> 50, ColorFunction -> (ColorData["CherryTones"][Rescale[#3, {-4, 4}]] &)],
ParametricPlot3D[Table[{x, y, F[x,y]}, {y, 0.2, 9.8, 0.2}], {x, 0, 10}, PlotStyle -> Red]
]
Plot[Integrate[F[x,y],{y,-20,+20}], {x, 0, 10}, PlotRange -> All, PlotStyle -> Red]
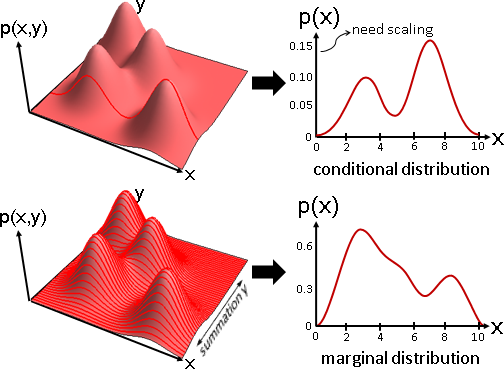
數學家發明了一些特殊觀點,可以幫忙分析聯合分布:
條件分布 conditional distribution:部分維度只看特定數值。
例如(X=x,Y)是垂直截面,(X,Y=y)是水平截面。(乘上適當倍率,調整成分布。)
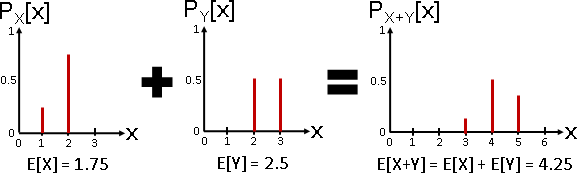
邊緣分布 marginal distribution :只看部分維度。
例如X是疊加水平截面,Y是疊加垂直截面。
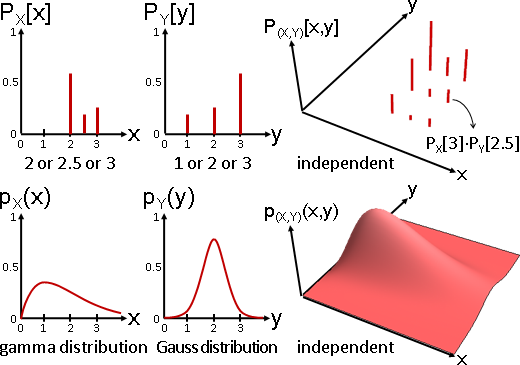
independent / uncorrelated
一個數組(x,y),拆成兩個數字x與y,只有唯一一種方式。
兩個數字x與y,併成一個數組(x,y),只有唯一一種方式。
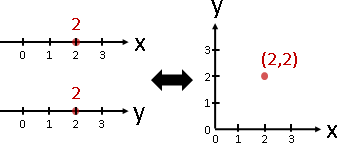
一個多變量隨機變數(X,Y),拆成兩個隨機變數X與Y,只有唯一一種方式:邊緣分布。
兩個隨機變數X與Y,併成一個多變量隨機變數(X,Y),卻有無限多種方式:(X,Y)的分布擁有無限多種可能性。
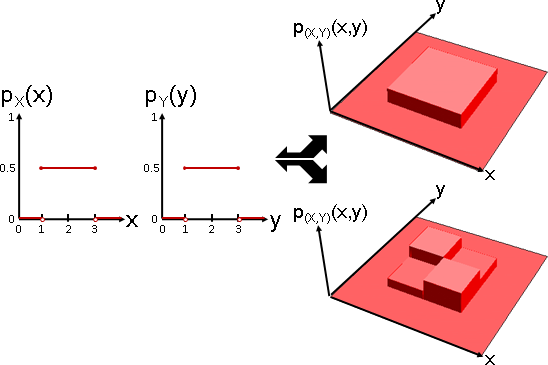
Plot3D[Piecewise[{{0.25, 1 < x < 3 && 1 < y < 3}}], {x, 0, 4}, {y, 0, 4}, PlotRange -> {0,1}, ExclusionsStyle -> Directive[Thick, Red], Boxed -> False, Mesh -> None, Axes -> False, PlotPoints -> 50, ColorFunction -> (ColorData["CherryTones"][Rescale[#3, {-4, 4}]] &)]
F[x_,y_] := Piecewise[{
{0.15, 1 < x < 2 && 1 < y < 2},
{0.35, 2 < x < 3 && 1 < y < 2},
{0.35, 1 < x < 2 && 2 < y < 3},
{0.15, 2 < x < 3 && 2 < y < 3}}];
Plot3D[F[x,y], {x, 0, 4}, {y, 0, 4}, PlotRange -> {0,1}, ExclusionsStyle -> Directive[Thick, Red], Boxed -> False, Mesh -> None, Axes -> False, PlotPoints -> 50, ColorFunction -> (ColorData["CherryTones"][Rescale[#3, {-4, 4}]] &)]
數學家從中挑選比較特別的款式,方便討論與運用:
獨立 independent :p(X,Y)(x,y) = pX(x)pY(y)
不相關 uncorrelated:E[XY] = 0
數學家的敘述方式是「兩個隨機變數X與Y是獨立的」,背後意義是「多變量隨機變數(X,Y)的分布是一種特殊款式:獨立」。
p = {{1, 1, 0.05}, {1.5, 1, 0.1}, {-1, -1, 0.1},
{-1, 0, 0.05}, {0, 1.5, 0.05}, {0, 0, 0.1},
{-1, -1.5, 0.2}, {1, -2, 0.15}, {-2, 1, 0.2}};
l = Table[Line[{p[[i]], {p[[i,1]], p[[i,2]], 0}}], {i,1,9}];
g = Show[ListPointPlot3D[{0,0,0}, Boxed -> False, Axes -> False, DataRange -> {{-2,2},{-2,2}}, PlotRange->{0,0.4}], Graphics3D[{Thickness[0.01], CapForm["Butt"], RGBColor[192,0,0], l}]]
img = ImageResize[Rasterize[g, "Image", ImageResolution -> 72*3], Scaled[1/3]];
ImageCrop[RemoveBackground[img, {{{0, 0}}, 0.1}]]
px = {{2, 0.6}, {3, 0.25}, {2.5, 0.15}};
py = {{3, 0.6}, {2, 0.25}, {1 , 0.15}};
pxy = {{2, 3, 0.6*0.6}, {2, 2, 0.6*0.25}, {2, 1, 0.6*0.15},
{3, 3, 0.25*0.6}, {3, 2, 0.25*0.25}, {3, 1, 0.25*0.15},
{2.5, 3, 0.15*0.6}, {2.5, 2, 0.15*0.25}, {2.5, 1, 0.15*0.15}};
l = Table[Line[{pxy[[i]], {pxy[[i,1]], pxy[[i,2]], 0}}], {i,1,9}];
g = Show[ListPointPlot3D[{0,0,0}, Boxed -> False, Axes -> False, PlotRange -> {{0,4},{0,4}}], Graphics3D[{Thickness[0.01], CapForm["Butt"], RGBColor[192,0,0], l}]]
img = ImageResize[Rasterize[g, "Image", ImageResolution -> 72*3], Scaled[1/3]];
ImageCrop[RemoveBackground[img, {{{0, 0}}, 0.1}]]
F[x_] := PDF[GammaDistribution[2, 1], x];
G[y_] := PDF[NormalDistribution[2, 0.5], y];
Plot[F[x], {x, 0, 4}, PlotRange -> {0,1}, Filling -> Axis]
Plot[G[y], {y, 0, 4}, PlotRange -> {0,1}, Filling -> Axis]
Show[
Plot3D[F[x]*G[y], {x, 0, 4}, {y, 0, 4}, PlotRange -> All, Boxed -> False, Mesh -> None, Axes -> False, PlotPoints -> 50, ColorFunction -> (ColorData["CherryTones"][Rescale[#3, {-4, 4}]] &)],
ParametricPlot3D[Table[{x, y, F[x]*G[y]}, {y, 0.1, 3.9, 0.1}], {x, 0, 4}, PlotStyle -> Red]
]
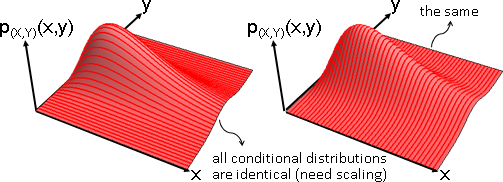
獨立:(X=x,Y=y)的出現程度,等於X=x的出現程度、Y=y的出現程度兩者相乘。
所有垂直截面皆相似、所有水平截面皆相似。
條件分布、邊緣分布,兩者相似(僅倍率不同,可以是零倍)。
無論有X沒X,都不影響Y的分布形狀,因而稱作獨立。
數學家很喜歡假設隨機變數是獨立的,讓分布變得很漂亮。
F[x_] := PDF[StudentTDistribution[1], x];
G[y_] := PDF[StudentTDistribution[1], y];
a = Cos[Pi/4]; b = Sin[Pi/4];
Plot3D[F[a*x-b*y]*G[b*x+a*y], {x, -5, 5}, {y, -5, 5}, PlotRange -> All, Boxed -> False, Mesh -> None, Axes -> False, PlotPoints -> 50, ColorFunction -> (ColorData["CherryTones"][Rescale[#3, {-4, 4}]] &)]
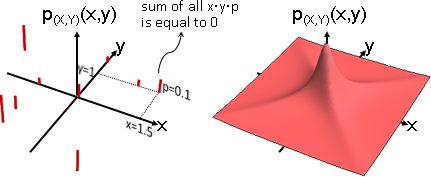
不相關:共相關數等於零。X與Y的點積是0。
共相關數 E[XY] :每個數組的XY相乘,求平均數。
正相關 E[XY] > 0:一三象限比較厚實。大致成正比。
負相關 E[XY] < 0:二四象限比較厚實。大致成反比。
不相關 E[XY] = 0:一三象限、二四象限,勢均力敵。
獨立較嚴格,不相關較寬鬆。獨立僅一種,不相關有多種。
有件事值得一提:當X或Y的平均數是零,獨立導致不相關。白話解釋是左右等量或者上下等量。
independent => uncorrelated if E[X] = 0 or E[Y] = 0
E[X] = sum x p(x)
ˣ
E[Y] = sum y p(y)
ʸ
E[XY] = sum sum x y p(x,y)
ˣ ʸ
= sum sum x y p(x) p(y) 獨立
ˣ ʸ
= sum sum x p(x) y p(y)
ˣ ʸ
= (sum x p(x)) (sum y p(y)) 交叉相乘
ˣ ʸ
= E[X]E[Y] = 0
不相關的定義有兩種:共相關數是零、共相關係數是零。後者直接得到「獨立導致不相關」的結論,省去「當平均數是零」的限制。
definition of "uncorrelated"
E[XY] = 0
another definition of "uncorrelated"
E[(X-E[X])(Y-E[Y])]
———————————————————————————— = 0
√ E[(X-E[X])²] E[(Y-E[Y])²]
transformation of multivariate random variable
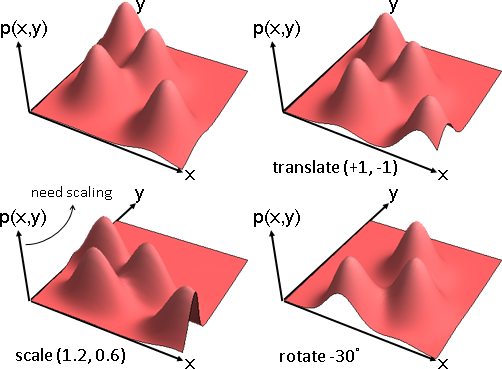
Plot3D[F[x/1.2,y/0.6], {x, 0, 10}, {y, 0, 10}, PlotRange -> All, Boxed -> False, Mesh -> None, Axes -> False, PlotPoints -> 50, ColorFunction -> (ColorData["CherryTones"][Rescale[#3, {-4, 4}]] &)]
t = Pi/6;
Plot3D[F[x*Cos[t]-y*Sin[t], x*Sin[t]+y*Cos[t]], {x, 0, 10}, {y, 0, 10}, PlotRange -> All, Boxed -> False, Mesh -> None, Axes -> False, PlotPoints -> 50, ColorFunction -> (ColorData["CherryTones"][Rescale[#3, {-4, 4}]] &)]
多變量隨機變數可以實施函數變換。雙射函數,浮動數字一齊改變,出現程度互不干涉,機率不必增減。
translate: (X+a, Y+b)
scale: (sX, tY)
rotate: (Xcosθ-Ysinθ, Xsinθ+Ycosθ)
多變量隨機變數可以實施仿射變換,變成不相關;但是無法變得獨立,只能變得盡量獨立。請見本站文件「principal component analysis」。
獨立、不相關的多變量隨機變數,實施仿射變換,性質可能保留或失效。
獨立 p(X,Y)(x,y) = pX(x)pY(y)
平移:仍然獨立 p(X,Y)(x+a,y+b) = pX(x+a)pY(y+b)
縮放:仍然獨立 p(X,Y)(sx,ty) = pX(sx)pY(ty)
旋轉:通常失效 p(X,Y)(xcosθ-ysinθ,xsinθ+ycosθ)
不相關 E[XY] = 0
平移:通常失效 E[(X+a)(Y+b)] = E[XY] + aE[Y] + bE[X] + ab
縮放:仍然不相關 E[(sX)(tY)] = stE[XY] = 0
旋轉:通常失效 E[(Xcosθ-Ysinθ)(Xsinθ+Ycosθ)] = (E[X²]-E[Y²])sinθcosθ
random vector
多個隨機變數,合稱「隨機向量」。
一個隨機變數推廣成多個隨機變數,衍生歧義:
多變量 multivariate :一個變數推廣成一個數組。重視聯合分布。
多變數 multivariable:一個變數推廣成多個變數。輕視聯合分布。