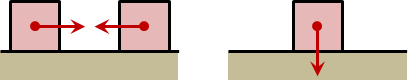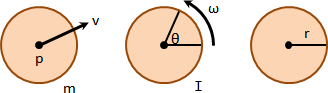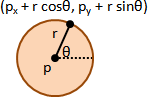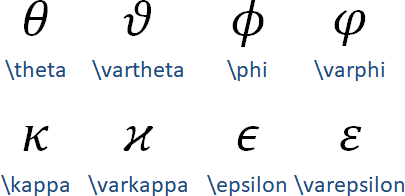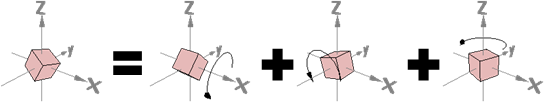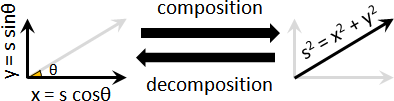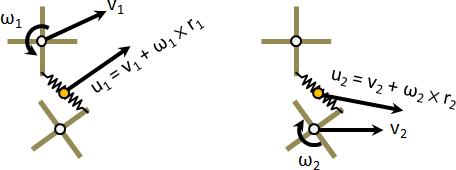simulation

模擬。真實現象化作數值，以數值模仿真實現象。

physically based simulation（motion simulation）

本文只談運動模擬。

知名軟體：

遊戲物理函式庫PyBullet、Box2D。

遊戲物理引擎Unreal Engine、NVIDIA PhysX。

機械設計軟體SolidWorks、Solid Edge、Siemens NX。

工程模擬軟體COMSOL、Moldex3D。

醫學模擬函式庫SOFA。

連體力學工具OpenFOAM。

知名公司：

工程模擬ANSYS、數位模型Autodesk、卡通動畫Disney。

相關主題以及所屬領域：

science                               科學
└ computer science                    計算機科學
  └ computer graphics                 計算機繪圖
    └ computer animation              計算機動畫
      └ physically based simulation   基於物理的模擬

science                                      科學
└ physics                                    物理
  └ mechanics                                力學
    └ computational mechanics                計算力學
      ├ computational solid mechanics        計算固體力學
      ├ computational contact mechanics      計算接觸力學
      ├ computational structural mechanics   計算結構力學
      └ computational fluid dynamics         計算流體力學
        └ computational fluid                計算流體力學模擬
           dynamics simulation              （氣體與液體的運動）

engineering                     工程
└ mechanical engineering        機械工程
  └ mechanical design           機構設計
    └ computer-aided design     電腦輔助設計
      └ mechanical simulation   機構模擬（機械裝置的運動）

matter

物質。佔據空間的東西。擁有特定的位置。

物質有時候會連成一團。

motion

運動。物質改變位置。

system

系統。大量物質，相互牽連。

system
├ structure   結構（不可動）
└ mechanism   機構（可動）

mechanics

力學。物質運動的學問。中文翻譯不到位。

位置、時刻、慣量，討論三者之間的關係。

mechanics
├ kinematics            運動學（位置、時刻）
├ statics               靜力學（位置、時刻、慣量）（運動未變化）
├ dynamics = kinetics   動力學（位置、時刻、慣量）（運動有變化）
└ continuum mechanics   連體力學（系統）
  ├ solid mechanics     固體力學（位置有限制）
  └ fluid mechanics     流體力學（位置未限制）

particle simulation

質點模擬、粒子模擬。物質可以平移。

資源

https://www.myphysicslab.com/

質點

牛頓發現運動定律F=ma。歐拉發現物質運動可以簡化成質心運動，物質軌跡等於質心軌跡。從質點開始介紹，事情比較簡單。

質點運動

質點。擁有位置、速度、加速度。

var x, y; // 位置 var vx, vy; // 速度 var ax, ay; // 加速度 function init() { x = canvas.width / 2; y = 0; vx = vy = 0; ax = ay = 0; }

移動。加速度改變了速度，速度改變了位置。

兩種方式：數值解（數值模擬）、符號解（公式解）。

兩者優缺點互補，通常採用數值模擬。優點：簡單明快。缺點：誤差逐步累積。

// 數值模擬：參數是時間差Δt const dt = 1; const g = 0.1; // 重力加速度 function update() { ax = 0; // 自由落體 ay = g; vx += ax * dt; vy += ay * dt; x += vx * dt; y += vy * dt; } // 公式解：參數是當前時刻t var t = 0; const g = 0.1; // 重力加速度 const dt = 1; // 時間增量 function update() { x = canvas.width / 2; y = 0.5 * g * t * t; // 自由落體公式 t += dt; }

步法。數值模擬，Δt並非無限微小，導致軌跡逐漸偏斜。大家發明各種步法，盡量撥正軌跡。

兩種步法：Euler method、Verlet method。

兩者優缺點互補，通常採用Euler method。優點：簡單明快。缺點：軌跡較歪。

// Euler method function update() { ax = 0; ay = g; // 先算新速度 vx += ax * dt; vy += ay * dt; // 再算新位置 x += vx * dt; y += vy * dt; } // Verlet method function update() { ax = 0; ay = g; // 先算新位置 var xnew = vx * dt + 0.5 * ax * dt * dt; var ynew = vy * dt + 0.5 * ay * dt * dt; // 再算新速度：位置差除以時間差，得到新速度。 vx = (xnew - x) / dt; vy = (ynew - y) / dt; x = xnew; y = ynew; }

時間。以無窮迴圈，更新時間、更新位置、重新繪圖。

兩種更新時間方式：定量增加（時間差Δt是定值）、浮動增加（時間t是當前時刻，時間差Δt是前後兩幀時刻差距）。

兩者優缺點互補，建議採用定量增加。優點：步伐穩定，軌跡端正。缺點：動畫播放速度不符合真實時間流逝。

// 定量改變 var t = 0; const dt = 1; function animate() { init(); frame(); } function frame() { // JavaScript動畫無窮迴圈 requestAnimationFrame(frame, canvas); update(); draw(); t += dt; // 當前時刻增加 } // 浮動改變 var t0, t, dt; function animate() { t0 = new Date().getTime(); init(); frame(); } function frame() { requestAnimationFrame(frame, canvas); t = new Date().getTime(); // 當前時刻 dt = t - t0; // 前後兩幀時刻差距 // if (dt > 0.2) dt = 0; // 避免飛天，暫停一下 t0 = t; update(); draw(); }

繪圖。質點畫成什麼形狀都行。質點位置視作像素座標。

// JavaScript畫布 var canvas = document.getElementById("Simulation1"); // JavaScript畫布繪圖工具 var ctx = canvas.getContext("2d"); function draw() { // 清屏 ctx.clearRect(0, 0, canvas.width, canvas.height); // 畫圓形 ctx.beginPath(); ctx.arc(x, y, 5, 0, 2.0 * Math.PI); // 塗紅色 ctx.fillStyle = "red"; ctx.fill(); // 描黑邊 ctx.strokeStyle = "black"; ctx.stroke(); }

質點施力

推進力。F = ma。

const m = 1; // 質量 function update() { var f = 1; // 力 ax = f / m; ay = 0; vx += ax * dt; vy += ay * dt; x += vx * dt; y += vy * dt; }

阻力。速度乘以阻力係數等於阻力。

const drag = 0.04; // 阻力係數 function update() { var f = 1; f += -drag * vx; // 阻力 ax = f / m; ay = 0; vx += ax * dt; vy += ay * dt; x += vx * dt; y += vy * dt; }

彈簧

彈力。可以類比為推進力。

虎克定律：位置差異乘以彈性係數等於彈力。

const length = 100; // 彈簧長度 const spring = 0.05; // 彈性係數 function update() { var d = Math.abs(y - y0); var f = -spring * (d - length); // 彈力 f += g; // 重力 ax = 0; ay = f / m; vx += ax * dt; vy += ay * dt; x += vx * dt; y += vy * dt; }

阻尼力。可以類比為阻力。

速度乘以阻尼係數等於阻尼力。

const damping = 0.02; // 阻尼係數 function update() { var d = Math.abs(y - y0); var f = -spring * (d - length); f += -damping * vy; // 阻尼力 f += g; ax = 0; ay = f / m; vx += ax * dt; vy += ay * dt; x += vx * dt; y += vy * dt; }

當力不在水平垂直方向，必須求得水平分量、垂直分量。

阻尼力，當速度不在彈簧方向，必須投影至彈簧方向。

function update() { var dx = x - x0; var dy = y - y0; var d = Math.sqrt(dx*dx + dy*dy); var fx = -spring * (d - length) * dx/d; var fy = -spring * (d - length) * dy/d; var dot = vx*dx + vy*dy; fx += -damping * (dot/d * dx/d); fy += -damping * (dot/d * dy/d); fy += g; ax = fx / m; ay = fy / m; vx += ax * dt; vy += ay * dt; x += vx * dt; y += vy * dt; }

平移、旋轉、縮放

幾何變換有三個獨立因素：平移、旋轉、縮放。

先前只介紹平移。此處同時使用平移、旋轉、縮放。

活用三種獨立因素，調整彈簧參數，製作各種動畫特效：

參數

參數。質量、長度、時間、彈性係數、阻尼係數，設定成真實世界的數值。讓螢幕座標、真實世界座標兩者一致。我沒有研究。

兩個需要考慮的項目：像素寬度與真實長度的比例（關鍵字dpi：一點佔多少英吋）、重新繪圖的時間間隔（關鍵字frame rate：一秒畫多少張圖）。

momentum

動量。質點運動強勁程度。

慣量ｘ速度＝動量。

inertia

慣量。質點運動強勁係數。

慣量取決於物質質地，各種物質有各種慣量。

force

力。動量變化快慢。

力不是指力氣大小。

質點施力之後的速度

牛頓發現p=mv與F=dp/dt。

物理學當中，動量p是質點運動強勁程度，力F是動量變化快慢。每當時間經過dt，動量差異是∫ F dt。原動量加上動量差異得到新動量。新動量p' = p + ∫ F dt。

計算學當中，動量p是已知數值，力F是自訂數值。無限微小的dt改成了一段範圍Δt。每當時間經過Δt，動量差異是F Δt。原動量加上動量差異得到新動量。新動量p' = p + F Δt。

計算學當中，dt改成Δt，導致計算結果錯誤。我們別無選擇，畢竟電腦無法處理無限微小的數字。

最後，以新動量求得新速度與新位置。

計算學當中，速度v是已知數值，慣量m是自訂數值。動量p = mv。新動量p' = p + F Δt。新速度v' = p' / m。

質點施力之後的速度

中學教科書將p=mv與F=dp/dt併成F=ma，精簡計算過程。

計算學當中，力F是自訂數值，慣量m是固定數值，加速度a是未知數值。力與慣量求得加速度。加速度求得新速度與新位置。

質點做平移運動的情況下，慣量叫做質量。

conservation of momentum

動量守恆。動量不會憑空出現憑空消失。動量總和固定。

一個質點的動量不會自行改變。其他質點對這個質點做了些事情，動量才會改變。

多個質點的動量不會自行改變。多個質點互相做了些事情，動量才會彼此傳遞，但是動量總和不會改變。當其他質點對這些質點做了些事情，動量總和才會改變。

action force / reaction force

兩個質點互相做了些事情。一個質點當主角，一個質點當配角。主角導致配角動量改變；其動量變化快慢，稱作作用力。配角導致主角動量改變；其動量變化快慢，稱作反作用力。作用力與反作用力，快慢相同，正負號相反。

此性質源自「動量守恆（動量不會憑空出現消失）（動量總和固定）」。主角動量減少，配角動量增加，才能使得動量總和固定。

力＝動量變化快慢。主角動量漸漸變少，配角動量漸漸變多。變化快慢必須一致，才能使得動量總和固定。

作用力和反作用力就是這麼樸實無華。中學教科書隱藏了p=mv，公開了F=ma，又換了說法，導致乍看像是天外飛來一筆：

兩個質點互相施力。一個質點當主角，一個質點當配角。主角施予配角的力，稱作作用力。配角施予主角的力，稱作反作用力。作用力與反作用力同時發生，方向相反。

examples of force

介紹幾個常見的力。

force               | equation       丨中文　丨意義
--------------------| ---------------丨一一一丨一一一一一一一一
gravitational force | F = Gm₁m₂/r²   丨引力　丨質心連線方向
gravitational force | F = mg         丨重力　丨g = Gm₂/r²

force               | equation       丨中文　丨意義
--------------------| ---------------丨一一一丨一一一一一一一一
restoring force     | F = -k‖x - x₀‖ 丨恢復力丨移位反方向
tension force       | F = -T         丨張力　丨繩索，移位反方向
buoyant force       | F = ρVg        丨浮力　丨外力反方向
--------------------| ---------------丨一一一丨一一一一一一一一
drag force          | F = k₁v + k₂v² 丨阻力　丨速度反方向
damping force       | F = -kv        丨阻尼力丨振盪，速度反方向
frictional force    | F = -μFₙ       丨摩擦力丨外力垂直方向

有些物理現象，擁有對應的力。英文文章有時為了方便，將物理現象當作是力。中文翻譯不做區隔，一律當作是力。

phenomenon           | force               丨意義
---------------------| --------------------丨一一一一一一一一一
gravity              | gravitational force 丨產生重量（的力）
to reach equilibrium | restoring force     丨恢復平衡（的力）
tension              | tension force       丨拉緊（所導致的力）
buoyancy             | buoyant force       丨上浮（的力）
drag                 | drag force          丨拖曳（所導致的力）
damping              | damping force       丨阻礙振盪（的力）
friction             | frictional force    丨摩擦（所導致的力）

projectile motion

拋體運動。一個質點運動，受到重力。

swinging motion

擺動。一個質點運動，受到重力，追加距離限制。

N-body motion

多體運動。多個質點運動，互相給予萬有引力。

目前沒有公式解，只能數值模擬。知名演算法是Barnes–Hut algorithm。

particle–particle–particle–mesh (P³M)
用頻譜法解Poisson equation。不適用於稀疏粒子。
fast multipole method
適度合併格子成為一個粒子。
Barnes–Hut algorithm
太遠的格子們（視角太小）視作一個粒子。

rigid body simulation

剛體模擬。物質具備特定造型，物質可以平移旋轉。

對應到運動學、靜力學、動力學。

資源

myPhysicsLab https://www.myphysicslab.com/engine2D/collision-en.html
Box2D        https://www.asc.ohio-state.edu/orban.14/processing_fall2016/roll.html
             https://natureofcode.com/book/chapter-5-physics-libraries/
             https://box2d.org/publications/
dyn4j        https://dyn4j.org/blog/
pyBullet     https://pybullet.org/wordpress/index.php/forum-2/
bepuphysics  https://www.bepuentertainment.com/
Simbody      https://simtk.org/docman/?group_id=47
SOFA         https://www.sofa-framework.org/community/doc/

剛體模擬

模擬流程。這些術語皆是計算學自創的。

壹、施力　　　　　　external force
　一、施加重力　　　├ net force calculation (e.g. gravity)
　二、更新速度　　　└ velocity update
貳、碰撞　　　　　　collision
　一、碰撞偵測　　　├ collision detection
　　　　　　　　　　└ collision resolution
　二、接觸位置求解　   ├ contact resolution
　三、動量轉移　　　   ├ momentum transport
　四、更新速度　　　   └ velocity update
參、更新位置

function update() { force(); collide(); move(); }

向量。建立資料結構。為了方便閱讀，我採取以下措施：

一、採用utility function，未採用access function（我不知道正確術語）。採用add(a, b)，未採用a.add(b)。

二、省略namespace。想要符合JavaScript編程哲學，請自行改成Vec2D.add(a, b)。

三、省略assignment。想要+=運算，請自行實作新函式addBy(a, b)。+=運算可以節省變數用量。

四、採用Unicode character。存檔時，請選擇UTF-8編碼。

function Vector(x,y) {this.x = x; this.y = y;} function length(a) {return Math.sqrt(a.x*a.x + a.y*a.y);} function negate(a) {return new Vector(-a.x, -a.y);} function scale(a,k) {return new Vector(a.x * k, a.y * k);} function add(a,b) {return new Vector(a.x + b.x, a.y + b.y);} function subtract(a,b) {return new Vector(a.x - b.x, a.y - b.y);} function dot(a,b) {return a.x*b.x + a.y*b.y;} function cross(a,b) {return a.x*b.y - a.y*b.x;} function perp(a) {return new Vector(-a.y, a.x);} function unit(a) { var l = length(a); if (l > 0) return new Vector(a.x / l, a.y / l); else return Object.create(a); } function rotate(a,θ) { var sinθ = Math.sin(θ); var cosθ = Math.cos(θ); return new Vector(a.x*cosθ - a.y*sinθ, a.x*sinθ + a.y*cosθ); }; var a = new Vector(1, 2); var b = new Vector(7, 8); var ab = subtract(b, a); // ab = b - a; console.log('ab = (', ab.x, ',' , ab.y, ')'); // U+01C1 Latin Letter Lateral Click var ǁabǁ = length(ab); console.log('ǁabǁ = ', ǁabǁ);

物體。建立資料結構。

var body_index = 0; function Body() { this.index = body_index++; this.shape = 'ball'; var x = Math.random() * canvas.width; var y = Math.random() * canvas.height; this.p = new Vector(x,y); // position this.v = new Vector(0,0); // velocity this.dv = new Vector(0,0); // change this.θ = 0; // angular position this.ω = 0; // angular velocity this.dω = 0; // change this.r = parameter.radius; // radius this.M = 1; // translational inertia this.invM = 1 / this.M; this.I = 0.4 * this.r * this.r * this.M; // rotational inertia this.invI = 1 / this.I; this.fixed = false; // fixed position } var balls = []; for (let i=0; i<parameter.N; i++) balls.push(new Body());

重力。速度加上重力加速度。

function force() { for (let b of balls) b.v.y += parameter.gravity * parameter.dt; }

碰撞。兩個物體，位置相互接觸，動量相互轉移。

var contacts = []; function collide() { // collision detection & contact resolution contacts = []; for (let b1 of balls) for (let b2 of balls) if (b1.index < b2.index) ball_ball_collision(b1, b2); // momentum transport for (let c of contacts) compute_impulse(c); for (let b of balls) apply_impulse(b); }

碰撞偵測。兩個物體，形狀相互重疊。

根據物體形狀，採用不同的演算法。

如果物體都是圓形：圓心距≤半徑和。

function ball_ball_collision(b1, b2) { var p12 = subtract(b2.p, b1.p); var ǁp12ǁ = length(p12); return ǁp12ǁ <= b1.r + b2.r; }

碰撞偵測。大量物體聚在一起，導致大量碰撞。

正經的做法：資料結構bounding volume hierarchy (BVH)，以便迅速找到所有正在碰撞的物體。

偷懶的做法：窮舉試誤，兩層迴圈。只有幾個物體而已，哎呀不用想那麼多啦。

function collide() { for (let b1 of balls) for (let b2 of balls) if (b1.index < b2.index) ball_ball_collision(b1, b2); ...... }

接觸位置求解。兩個物體，形狀相互接觸。

一、決定誰攻誰防。一般來說，頂點進攻，表面防禦。

二、進攻物體挪至防禦物體表面，沿著表面垂直方向。

根據物體形狀，採用不同的演算法。

如果物體都是圓形：圓心連線與圓周的交點。

var contacts = []; function ball_ball_collision(b1, b2) { var p12 = subtract(b2.p, b1.p); var ǁp12ǁ = length(p12); var d = b1.r + b2.r - ǁp12ǁ; // penetrating depth if (d < 0) return; // no collision var n = scale(p12, 1/ǁp12ǁ); // normal vector var r1 = scale(n, +b1.r); // contact vector var r2 = scale(n, -b2.r); // var c1 = add(b1.p, r1); // contact // var c2 = add(b2.p, r2); contacts.push([b1, b2, r1, r2, n, d]); }

接觸位置求解。大量物體聚在一起，導致連鎖挪動、反覆挪動。

正經的做法：方程組求解。不過我沒有學會。

偷懶的做法：不挪動物體，只找接觸位置。物體碰撞之後，物體自然分開。物體稍微重疊一段時間，無傷大雅。

偷懶的做法

動量轉移。兩個物體，位置相互靠緊，動量相互轉移。

function collide() { ...... // momentum transport for (let c of contacts) compute_impulse(c); for (let b of balls) apply_impulse(b); }

計算衝量。根據接觸位置、接觸速度，計算動量轉移量。

本文採用Mirtich's algorithm。原理延後介紹。

納入考慮的物理現象：移動、轉動、恢復、摩擦。

normal impulse:
                -(e+1) (u₁₂∙N)
Jɴ = ———————————————————————————————————————
     m₁⁻¹ + m₂⁻¹ + I₁⁻¹(r₁×N)² + I₂⁻¹(r₂×N)²

tangent impulse:
                 -(e+1) (u₁₂∙T)
Jᴛ = ———————————————————————————————————————
     m₁⁻¹ + m₂⁻¹ + I₁⁻¹(r₁×T)² + I₂⁻¹(r₂×T)²

Jᴛ = min(Jᴛ, +μJɴ)

Jᴛ = max(Jᴛ, -μJɴ)

r₁ r₂ relative position of contact and body
u₁₂   relative velocity at contact
N     normal vector at contact
T     tangent vector at contact
m₁ m₂ translational inertia (mass)
I₁ I₂ rotational inertia (moment of inertia)
e     coefficient of restitution
μ     coefficient of friction

function compute_impulse([b1, b2, r1, r2, n, d]) { // tangent vector var t = perp(n); // relative velocity var v12 = subtract(b2.v, b1.v); var ω12 = scale(t, b2.ω * b2.r - b1.ω * b1.r); var u12 = add(v12, ω12); // normal impulse var r1xn = cross(r1, n); var r2xn = cross(r2, n); var kn = b1.invM + b2.invM + b1.invI * r1xn * r1xn + b2.invI * r2xn * r2xn; var Jn = dot(u12, n) * (1 + parameter.restitution) / kn; // tangent impulse var r1xt = cross(r1, t); var r2xt = cross(r2, t); var kt = b1.invM + b2.invM + b1.invI * r1xt * r1xt + b2.invI * r2xt * r2xt; var Jt = dot(u12, t) * (1 + parameter.restitution) / kt; var f = parameter.friction * Jn; Jt = Math.sign(Jt) * Math.min(Math.abs(Jt), Math.abs(f)); ...... }

彈簧力。追加額外衝量，強制分開物體，避免物體重疊卡住。

侵入越深，彈簧力越強。設置彈簧力上限，避免物體暴衝。

function compute_impulse([b1, b2, r1, r2, n, d]) { ...... // spring force var s = Math.min(d, parameter.depth); var k = -parameter.spring * s; if (Jn * k < 0) Jn = k; ...... }

累計衝量。一個物體同時碰撞多個物體，需要累計衝量。

方便起見，衝量換算成速度。

Δv = m⁻¹JɴN
Δω = I⁻¹Jɴ(r×N) + I⁻¹Jᴛ(r×T)

function compute_impulse([b1, b2, r1, r2, n, d]) { ...... // change in velocity var dv = scale(n, Jn * b1.invM); b1.dv.x += dv.x; b1.dv.y += dv.y; b1.dω += r1xn * Jn * b1.invI + r1xt * Jt * b1.invI; var dv = scale(n, Jn * b2.invM); b2.dv.x -= dv.x; b2.dv.y -= dv.y; b2.dω -= r2xn * Jn * b2.invI - r2xt * Jt * b2.invI; }

更新速度。

function apply_impulse(b) { b.v.x += b.dv.x; b.v.y += b.dv.y; b.ω += b.dω; b.dv.x = b.dv.y = b.dω = 0; }

牆壁。物體碰撞牆壁。物體速度變號變慢。

釘住不動的物體，視作質量極大，導致碰撞之後速度幾乎不變。如此一來，得以沿用動量轉移的程式碼，不必撰寫速度變號變慢的程式碼。

var wall = new Body(); wall.shape = 'wall'; wall.fixed = true; function ball_wall_collision(b, w) { var x1 = b.r, x2 = canvas.width - b.r; var y1 = b.r, y2 = canvas.height - b.r; if (b.p.x <= x1) macro(new Vector(-1,0), x1 - b.p.x); else if (b.p.x >= x2) macro(new Vector(+1,0), b.p.x - x2); if (b.p.y <= y1) macro(new Vector(0,-1), y1 - b.p.y); else if (b.p.y >= y2) macro(new Vector(0,+1), b.p.y - y2); function macro(n, d) { var r1 = scale(n, b.r); var r2 = scale(n, -1.0); contacts.push([b, w, r1, r2, n, d]); } } function compute_impulse([b1, b2, r1, r2, n, d]) { // reciprocal of mass/inertia var invM1, invM2, invI1, invI2; if (b1.fixed) { invM1 = 1e-9; invI1 = 1e-9; } else { invM1 = b1.invM; invI1 = b1.invI; } if (b2.fixed) { invM2 = 1e-9; invI2 = 1e-9; } else { invM2 = b2.invM; invI2 = b2.invI; } ...... // change in velocity if (!b1.fixed) { var dv = scale(n, Jn * invM1); b1.dv.x += dv.x; b1.dv.y += dv.y; b1.dω += r1xn * Jn * invI1 + r1xt * Jt * invI1; } if (!b2.fixed) { var dv = scale(n, Jn * invM2); b2.dv.x -= dv.x; b2.dv.y -= dv.y; b2.dω -= r2xn * Jn * invI2 - r2xt * Jt * invI2; } }

避免穿牆。先結算物體與物體碰撞的新速度，才計算物體與牆壁碰撞的新速度。如此一來，有效避免物體被擠入牆。

var contacts = []; function collide() { // ball-ball contacts = []; for (let b1 of balls) for (let b2 of balls) if (b1.index < b2.index) ball_ball_collision(b1, b2); for (let c of contacts) compute_impulse(c); for (let b of balls) apply_impulse(b); // ball-wall contacts = []; for (let b of balls) ball_wall_collision(b, wall); for (let c of contacts) compute_impulse(c); for (let b of balls) apply_impulse(b); }

更新位置。

function move() { for (let b of balls) { b.p.x += b.v.x; b.p.y += b.v.y; b.θ += b.ω; } }

繪圖。根據物體形狀，採用不同的繪圖方式。

如果物體是圓形：一個圓周、一個半軸（呈現轉動）。

function drawBalls() { ctx.clearRect(0, 0, canvas.width, canvas.height); ctx.fillStyle = 'orange'; ctx.strokeStyle = 'black'; ctx.lineWidth = 1; for (let b of balls) { // circle ctx.beginPath(); ctx.arc(b.p.x, b.p.y, b.r, 0, Math.PI * 2, true); ctx.fill(); ctx.stroke(); // axis ctx.beginPath(); ctx.moveTo(b.p.x, b.p.y); ctx.lineTo(b.p.x + b.r * Math.cos(b.θ), b.p.y + b.r * Math.sin(b.θ)); ctx.stroke(); } }

動量轉移

牛頓發現p=mv。動量＝慣量ｘ速度。

慣量和速度是已知數。

p = mv

兩物各自擁有動量。

⎰ p₁ = m₁v₁      第一物
⎱ p₂ = m₂v₂      第二物

碰撞之後，一物動量減少，另一物動量增加。

動量的轉移量，稱作衝量。

⎰ p₁' = p₁ - J   第一物
⎱ p₂' = p₂ + J   第二物

找出衝量，得以計算新動量，得以計算新速度。

⎰ p₁' = m₁v₁'  --->  ⎰ v₁' = p₁' / m₁   第一物
⎱ p₂' = m₂v₂'        ⎱ v₂' = p₂' / m₂   第二物

本文採用Mirtich's algorithm計算衝量。演算法源自這篇論文：

《Impulse-based Dynamic Simulation of Rigid Body System》

動量轉移：移動

物體碰撞視作接觸位置碰撞。物體速度等於接觸位置速度。

衝量公式。衝量＝速度差先後差異／質量倒數和。

    (v₂' - v₁') - (v₂ - v₁)
J = ———————————————————————
           m₁⁻¹ + m₂⁻¹

恢復。恢復係數＝－舊相對速度／新相對速度。

v₂' - v₁' = -e (v₂ - v₁)

求得衝量：

       -(1+e) (v₂ - v₁)
J = ———————————————————————
          m₁⁻¹ + m₂⁻¹

求得新速度：

           J 
v₁' = v₁ - ——
           m₁

           J 
v₂' = v₂ + ——
           m₂

衝量公式推導過程：

m                    慣量（純量）
v                    速度（向量）
p = mv               動量（向量）

v                    速度，碰撞之前
p  = mv              動量，碰撞之前
v'                   速度，碰撞之後
p' = mv'             動量，碰撞之後

p  = mv              碰撞之前
p' = mv'             碰撞之後
p' - p = mv' - mv    先後差異
p' - p = m(v' - v)   提項
Δp     = mΔv         簡寫

⎧ Δp₁ = m₁Δv₁        第一物
⎨ Δp₂ = m₂Δv₂        第二物
⎩ J = -Δp₁ = Δp₂     衝量（動量轉移量）

⎧ Δp₁ / m₁ = Δv₁     第一物
⎨ Δp₂ / m₂ = Δv₂     第二物
⎩ J = -Δp₁ = Δp₂     衝量（動量轉移量）

⎰ -J / m₁ = Δv₁      第一物
⎱  J / m₂ = Δv₂      第二物

J / m₁ + J / m₂ = Δv₂ - Δv₁   二式減一式
J / m₁ + J / m₂ = Δv₁₂        請見下面
J (1/m₁ + 1/m₂) = Δv₁₂        提項
J = Δv₁₂ / (1/m₁ + 1/m₂)      移項
J = Δv₁₂ / (m₁⁻¹ + m₂⁻¹)      得證

Δv₂ - Δv₁ = (v₂' - v₂) - (v₁' - v₁)   展開
Δv₂ - Δv₁ = (v₂' - v₁') - (v₂ - v₁)   移項
Δv₂ - Δv₁ = v₁₂' - v₁₂                簡寫（相對速度）
Δv₂ - Δv₁ = Δv₁₂                      簡寫（先後差異）

動量轉移：移動轉動

方才只有移動。現在引入轉動。

作者假設平移衝量和旋轉衝量恰好相等（不合理）。

衝量公式。

        (u₂' - u₁') - (u₂ - u₁)
J = —————————————————————————————————
    M₁⁻¹ + M₂⁻¹ - R₁I₁⁻¹R₁ - R₂I₂⁻¹R₂

恢復。

u₂' - u₁' = -e (u₂ - u₁)

求得衝量：

            -(1+e) (u₂ - u₁)
J = —————————————————————————————————
    M₁⁻¹ + M₂⁻¹ - R₁I₁⁻¹R₁ - R₂I₂⁻¹R₂

求得新速度：

v₁' = v₁ - m₁⁻¹J
v₂' = v₂ + m₂⁻¹J
ω₁' = ω₁ - I₁⁻¹R₁J
ω₂' = ω₂ + I₂⁻¹R₂J

衝量公式推導過程：

v                    平移速度（向量）
ω                    旋轉速度（向量）（垂直於旋轉平面）
r                    旋轉半徑向量（向量）
u = v + (ω × r)      接觸速度

p = mv               平移動量
L = Iω               旋轉動量

⎧ Δu = Δv + Δω × r   接觸速度先後差異
⎨ Δp = m Δv          平移衝量
⎩ ΔL = I Δω          旋轉衝量

⎧ Δu = Δv + Δω × r   接觸速度先後差異
⎨ m⁻¹ Δp = Δv        平移衝量
⎩ I⁻¹ ΔL = Δω        旋轉衝量

Δu = m⁻¹ Δp + (I⁻¹ ΔL) × r

when ΔL = r × Δp                   當平移衝量和旋轉衝量恰好相等（不合理）
Δu = m⁻¹ Δp + (I⁻¹ (r × Δp)) × r   代入
Δu = m⁻¹ Δp - r × (I⁻¹ (r × Δp))   對調
Δu = m⁻¹ Δp - R I⁻¹ R Δp           叉積改成矩陣（R是叉積矩陣）
Δu = M⁻¹ Δp - R I⁻¹ R Δp           倍率改成矩陣（M是質量矩陣）
Δu = (M⁻¹ - RI⁻¹R) Δp              提項

    ⎡  0  -r₞  r₝ ⎤
R = ⎢  r₞  0  -rₓ ⎥   cross product matrix
    ⎣ -r₝  rₓ  0  ⎦

    ⎡ m 0 0 ⎤
M = ⎢ 0 m 0 ⎥   mass matrix
    ⎣ 0 0 m ⎦

⎧ Δu₁ = Δv₁ + r₁ × Δω₁   第一物接觸速度先後差異
⎪ Δp₁ = m₁ Δv₁           第一物平移衝量
⎪ ΔL₁ = I₁ Δω₁           第一物旋轉衝量
⎪ ΔL₁ = r₁ × Δp₁         第一物平移衝量等於旋轉衝量（不合理）
⎨ Δu₂ = Δv₂ + r₂ × Δω₂   第二物接觸速度先後差異
⎪ Δp₂ = m₂ Δv₂           第二物平移衝量
⎪ ΔL₂ = I₂ Δω₂           第二物旋轉衝量
⎪ ΔL₂ = r₂ × Δp₂         第二物平移衝量等於旋轉衝量（不合理）
⎩ J = -Δp₁ = Δp₂         衝量

J = (M₁⁻¹ + M₂⁻¹ - R₁I₁⁻¹R₁ - R₂I₂⁻¹R₂)⁻¹ (Δu₂ - Δu₁) 二減一
J = (M₁⁻¹ + M₂⁻¹ - R₁I₁⁻¹R₁ - R₂I₂⁻¹R₂)⁻¹ Δu₁₂        得證

動量轉移：移動轉動、考慮摩擦

方才只有恢復。現在引入摩擦。

摘自這本書籍、這份講義。

作者假設牛頓動量和庫侖摩擦可以併用（不合理）。

二維。法線分量、切線分量。

                 -(e+1) (u₁₂∙N)
Jɴ = ———————————————————————————————————————
     m₁⁻¹ + m₂⁻¹ + I₁⁻¹(r₁×N)² + I₂⁻¹(r₂×N)²

                 -(e+1) (u₁₂∙T)
Jᴛ = ———————————————————————————————————————
     m₁⁻¹ + m₂⁻¹ + I₁⁻¹(r₁×T)² + I₂⁻¹(r₂×T)²

摩擦。法線衝量ｘ摩擦係數＝切線衝量上限。

-μJɴ ≤ Jᴛ ≤ +μJɴ

新速度：

v₁' = v₁ + m₁⁻¹JɴN
v₂' = v₂ - m₂⁻¹JɴN
ω₁' = ω₁ + I₁⁻¹Jɴ(r₁×N) + I₁⁻¹Jᴛ(r₁×T)
ω₂' = ω₂ - I₂⁻¹Jɴ(r₁×N) - I₂⁻¹Jᴛ(r₁×T)

物理學當中，附帶摩擦的碰撞，其數學模型尚未定案。

計算學當中，自創簡易模型，自創演算法，作為折衷方案。

雖然諸多不合理，但是大家並不在意。畢竟是折衷方案。

知名專案Box2D（程式碼）和myPhysicsLab採用此演算法。

缺陷

運動模擬，時間只能離散變化，不能連續變化。物體只能離散運動，不能連續運動。離散運動導致諸多問題，以下逐一介紹。

缺陷：penetration

離散運動導致一個物體侵入另一個物體。

一類解法是玩弄Δt。

解法一：Δt是定值。降低Δt。以便降低移動距離，以便降低侵入深度。缺點是frame rate上升，計算時間變久。

解法二：Δt不是定值。求得Δt。方程式求解，求得碰撞時刻。缺點是Δt不是定值，也就無法控制frame rate。

解法二當中，當物體只會移動、不會轉動，可以利用raycasting求解：第一物各個頂點，沿著相對速度方向，射出射線，嘗試射中第二物。

另一類解法是挪動物體。

解法三：將侵入者挪到表面，沿著表面法向量。挪動過程可能導致連鎖侵入。方程組求解，求得接觸位置們。缺點是計算時間較久。

解法四：讓侵入者盡快離開，給予額外動量。採用彈簧力，侵入越深，動量越大。缺點是動量不守恆、物體像水一樣難以靜止。

解法四當中，彈簧力與重力嚴重影響外觀。需要仔細調整參數。

調整彈簧力。彈簧力太小，物體無法撐起，宛如醬油膏。彈簧力太大，物體一碰就飛，宛如爆米花。

調整重力。重力越小，速度越小，侵入越小，宛如慢動作播放。搞成了解法一。重力越大，速度越大，侵入越多，彈簧力越大，宛如爆米花。解法是設定彈簧力上限。

缺陷：jittering

速度太快，大幅侵入另一個物體。碰撞之後，相對速度變號並且減慢。導致物體來不及脫離。導致物體持續碰撞。物體持續更換相對速度方向。物體持續來回抖動。

解法同前。沒有侵入就沒有抖動。

缺陷：tunneling

速度太快，形狀太薄。導致一個物體穿越另一個物體。侵入過頭了，偵測不到碰撞。

解法一：物體運動範圍，形成外框。以此外框實施碰撞偵測。稱作speculative collision。

解法二：玩弄Δt。先前提到的解法一與解法二。

缺陷：infinite bouncing

物體受到重力。每單位時間Δt，動量（速度）追加定值。

物體碰撞地面。動量散失（速度減慢），反彈高度降低。

每單位時間Δt，碰撞次數持續增加，卻總是只算到一次。導致動量削減不足。導致動量無法歸零。物體持續反彈，永不止息。

目前無解。

缺陷：stack bouncing

承上。重力加速度太大（動量追加太多），或者，恢復係數太大（動量散失比例太少），即便是靜止物體互相堆疊，也會infinite bouncing，外觀如同jittering。

目前無解。

缺陷：collision sequence

多個物體，連環碰撞。

找到Δt之內的碰撞順序，NP-hard。

解法：放棄治療。當作是同時碰撞。

缺陷：simultaneous collisions

多個物體，同時碰撞。

碰撞順序不同，新速度不同。

解法：以任意順序逐一計算各個碰撞。不即時更新速度。所有碰撞處理完畢之後，再一口氣更新速度。

缺陷：simultaneous contacts

兩個物體，多處同時碰撞。

解法：放棄治療。解法同上。

架構

rotation
├ rotation by coordinates
├ rotation by spin
│  └ vector / quaternion
└ rotation by 3 spins (Euler angles)
   ├ Z-Y-X / Z-X-Z
   └ extrinsic rotation / intrinsic rotation

rotation

旋轉。既是物理學詞彙，亦是數學詞彙。本文介紹數學旋轉。

coordinates

座標。圓周、球面，建立座標系統。

二維圓周座標：一個角度θ。

逆時針方向，角度範圍0°到360°。

三維球面座標：兩個角度θ與φ。

水平角度θ，角度範圍-180°到+180°，稱作方位角azimuth。鉛直角度φ，角度範圍-90°到+90°，稱作高度角altitude。數學符號造型符合角度方向，非常漂亮。

順帶一提，圓周座標／球面座標，額外配合半徑長度r，得以表達二維平面／三維空間每一個位置，稱作極座標／球座標。

極座標化作二維平面座標。（反方向比較複雜，此處省略。）

x = r cosθ
y = r sinθ

球座標化作三維空間座標。（反方向比較複雜，此處省略。）

x = r cosφ cosθ
y = r cosφ sinθ
z = r sinφ

數學當中，利用三角函數，將角度化作長度。

rotation by coordinates

二維旋轉的簡易表示法：一個角度。

旋轉前與旋轉後的角度差異。

三維旋轉有許多方向，無法表示成兩個角度。

需要其他方法。

數學當中，旋轉可以寫成矩陣。正規正交矩陣，容積+1。

二維旋轉是2x2矩陣。分別計算兩個標準座標軸的旋轉結果，求得矩陣數值。

⎡ x' ⎤ = ⎡ cosθ -sinθ ⎤ ⎡ x ⎤
⎣ y' ⎦   ⎣ sinθ  cosθ ⎦ ⎣ y ⎦

三維旋轉是3×3矩陣。分別計算三個標準座標軸的旋轉結果，求得矩陣數值。僅以兩個角度，無法計算矩陣數值。需要其他方法。

⎡ x' ⎤   ⎡ ? ? ? ⎤ ⎡ x ⎤
⎢ y' ⎥ = ⎢ ? ? ? ⎥ ⎢ y ⎥
⎣ z' ⎦   ⎣ ? ? ? ⎦ ⎣ z ⎦

spin

自旋。一個轉軸（向量）、一個轉角（純量），沿著轉軸旋轉。

自旋有兩種計算方式：向量、四元數。

向量：Rodrigues's formula。

v' = v cosθ + (e × v) sinθ + e (e ∙ v) (1 - cosθ)

進一步使用Rodrigues's formula求得矩陣。

v' = R v

R = I + sinθ E + (1 - cosθ) E²

    ⎡  0  -e₞  e₝ ⎤
E = ⎢  e₞  0  -eₓ ⎥
    ⎣ -e₝  eₓ  0  ⎦

(Ev = e × v)

四元數：Hamilton product。

a + bi + cj + dk。a b c d是實數。i j k是虛數。

虛數乘法規則如下所示。

  | 1   i   j   k
--+---------------
1 | 1   i   j   k     i² = j² = k² = ijk = -1
i | i  −1   k  −j     ij =  k , jk =  i , ki =  j
j | j  −k  −1   i     ji = -k , kj = -i , ik = -j
k | k   j  −i  −1

自旋是四元數的共軛乘法q p q⁻¹。

向量 v = (vₓ,v₝,v₞)  <=>  v = 0 + vₓi + v₝j + v₞k
轉軸 e = (eₓ,e₝,e₞)  <=>  e = 0 + eₓi + e₝j + e₞k
轉角 θ
自旋 v' = q v q⁻¹
　　 q = exp(e ½θ)
　　   = cos(½θ) + eₓsin(½θ)i + e₝sin(½θ)j + e₞sin(½θ)k

多個四元數可以併成一個四元數，如同矩陣。

v' = q₃ q₂ q₁ v q₁⁻¹ q₂⁻¹ q₃⁻¹ = q v q⁻¹
where q = q₃ q₂ q₁

進一步使用Euler–Rodrigues formula求得矩陣。

     ⎡ a²+b²-c²-d² 2(bc-ad)    2(bd+ac)    ⎤
v' = ⎢ 2(bc+ad)    a²+c²-b²-d² 2(cd-ab)    ⎥ v
     ⎣ 2(bd-ac)    2(cd+ab)    a²+d²-b²-c² ⎦

a = cos(½θ)
b = eₓ sin(½θ)
c = e₝ sin(½θ)
d = e₞ sin(½θ)
(a²+b²+c²+d² = 1)

rotation by spin

根據Euler's rotation theorem，一次旋轉等價於一次自旋。

三維旋轉的簡易表示法：一個轉軸e、一個轉角θ。

設定兩個向量，從一個向量旋轉至另一個向量。兩個向量形成一個平面。兩個向量的叉積，得到平面法向量，作為轉軸。兩個向量的夾角，作為轉角。旋轉化作自旋。

三維旋轉的另一種簡易表示法：三個角度。

兩個角度當作轉軸方向，一個角度當作轉角。

rotation by 3 spins

數學幾何變換，不考慮軌跡。物理運動，需要考慮軌跡。

上述旋轉表示法，設計成機械，軌跡不流暢，操控不直覺。

因此大家將一次旋轉化作三次自旋。以標準座標軸作為轉軸。

轉軸次序有兩種方式：

實務上採用Z-Y-X。

Z-Y-X：標準座標軸作為轉軸。（Tait–Bryan angles）
Z-X-Z：第一轉軸、第三轉軸，兩者相同。（Euler angles）

轉軸動向有兩種方式：

計算機採用extrinsic rotation。機械採用intrinsic rotation。

extrinsic rotation：沿著世界座標軸自旋（所有轉軸固定不動）。
intrinsic rotation：沿著物體座標軸自旋（其餘轉軸隨之旋轉）。

接下來詳細介紹Z-Y-X。

三次自旋。三個轉軸是Z軸、Y軸、X軸。三個轉角稱作偏航角yaw、俯仰角pitch、橫滾角roll。

具體形象如下圖。X軸機身，Y軸機翼，Z軸天地。

自旋的轉軸恰是標準座標軸，其矩陣恰是Givens matrix。矩陣數值如同二維旋轉。簡單明瞭。不需要Rodrigues's formula。

        ⎡ 1  0     0   ⎤
Rx(θ) = ⎢ 0 cosθ -sinθ ⎥   roll
        ⎣ 0 sinθ  cosθ ⎦   (spin around x-axis)

        ⎡  cosθ 0 sinθ ⎤
Ry(θ) = ⎢   0   1  0   ⎥   pitch
        ⎣ -sinθ 0 cosθ ⎦   (spin around y-axis)

        ⎡ cosθ -sinθ 0 ⎤
Rz(θ) = ⎢ sinθ  cosθ 0 ⎥   yaw
        ⎣  0     0   1 ⎦   (spin around z-axis)

三次自旋，即是三個矩陣連乘，從右往左。

  Rx(α) Ry(β) Rz(γ)

  ⎡ 1  0     0   ⎤ ⎡  cosβ 0 sinβ ⎤ ⎡ cosγ -sinγ 0 ⎤
= ⎢ 0 cosα -sinα ⎥ ⎢   0   1  0   ⎥ ⎢ sinγ  cosγ 0 ⎥
  ⎣ 0 sinα  cosα ⎦ ⎣ -sinβ 0 cosβ ⎦ ⎣  0     0   1 ⎦
  roll             pitch            yaw

矩陣連乘順序，左右顛倒，extrinsic rotation就變成intrinsic rotation。

gimbal lock

環架gimbals：三個環，對應三個轉軸。當一個環自旋，所有外環轉軸固定不動，相當方便。紀錄三個環的三個旋角，完成旋轉。

環架鎖定gimbal lock：環架的重大缺陷。當其中兩個環對齊，則旋轉方位短少，變成一個。

三次自旋也有相同缺陷。例如俯仰角是±90°，則旋轉方位短少，變成一個。

無論轉軸次序是Z-Y-X、Z-X-Z，無論轉軸動向是世界座標軸、物體座標軸，都無法避免gimbal lock。

簡易理解方式：寫下三個自旋矩陣，然後設定適當的轉角，使得矩陣相乘結果，恰好退化成一個自旋矩陣。

let β = π/2

    ⎡ 1  0     0   ⎤ ⎡  cosβ 0 sinβ ⎤ ⎡ cosγ -sinγ 0 ⎤
R = ⎢ 0 cosα -sinα ⎥ ⎢   0   1  0   ⎥ ⎢ sinγ  cosγ 0 ⎥
    ⎣ 0 sinα  cosα ⎦ ⎣ -sinβ 0 cosβ ⎦ ⎣  0     0   1 ⎦
    roll             pitch            yaw

    ⎡ 1  0     0   ⎤ ⎡  0 0 1 ⎤ ⎡ cosγ -sinγ 0 ⎤
  = ⎢ 0 cosα -sinα ⎥ ⎢  0 1 0 ⎥ ⎢ sinγ  cosγ 0 ⎥
    ⎣ 0 sinα  cosα ⎦ ⎣ -1 0 0 ⎦ ⎣  0     0   1 ⎦

    ⎡    0        0      1 ⎤
  = ⎢  sin(α+γ) cos(α+γ) 0 ⎥
    ⎣ -cos(α+γ) sin(α+γ) 0 ⎦

gimbal lock引發許多問題。例如登月太空船Apollo 11因而難以瞄準星星進行定位。太空人操作定位儀器，每當快要產生gimbal lock，系統就會拉警報。太空人當場表示：「給我第四個gimbal當作聖誕禮物好不好。」也許他想起某首聖誕歌曲。

如何避免gimbal lock，尚無定論。大家各顯神通。也有人選擇放棄三次自旋，回到一次自旋。

順帶一提，網路上謠傳四元數可以避免gimbal lock。謠言主要來自遊戲設計論壇。大概是遊戲腦吧。

spherical interpolation

數學當中，旋轉軌跡可以寫成內插。稱作球面內插。

二維旋轉軌跡，即是轉角內插。時刻範圍0到1。

θₜ = (1 - t) θ₁ + t θ₂
where θ₁ = 0 , θ₂ = θ , t = [0,1]

θₜ = t θ

三維旋轉軌跡，即是轉角內插。轉軸保持一致。

θₜ = t θ
eₜ = e

三次自旋軌跡，則是三個轉角各自內插。

αₜ = t α
βₜ = t β
γₜ = t γ

大家經常使用一次內插，稱作球面一次內插spherical linear interpolation，簡寫slerp。

spin is not commutative

commutative是線性代數的術語：某些特殊的矩陣，其矩陣乘法可以自由對調先後次序，不影響計算結果。AB=BA。

一般的矩陣，無法自由對調先後次序。AB≠BA。

三次自旋，旋轉次序不同，旋轉結果不同。

球面內插，三個轉角依序改變、同時改變，旋轉結果也不同。

我沒有查到相關資料。

rigid transformation

數學當中，又旋轉、又平移，稱作剛體變換。

剛體變換可以改成自旋與平移。

Euler's rotation theorem：旋轉＝自旋。

三維旋轉矩陣R，容積det(R) = +1，其中一個特徵值是+1，其特徵向量是實數。旋轉之後此特徵向量保持不動，即是轉軸。

Chasles's theorem：旋轉＋平移＝繞軸自旋＋沿軸平移。

我沒有學會證明過程。

延伸閱讀：希臘字母phi的造型

TeX的分類方式是正體與變體。詳情請見TeX符號清單。

Unicode的分類方式是書寫慣例與額外符號。詳情請見Unicode第25號技術報告2.3.1節。

這兩種分類方式，phi的開闔不一致！

各種電腦字型當中，有些沿襲TeX的風格，有些跟進Unicode的規定，導致U+03C6 φ與U+03D5 ϕ顯示結果不同，開闔不一致，成為歷史共業。詳情請見維基百科。

架構

collision detection
├ continuous collision detection
└ discrete collision detection
  ├ broad-phase collision detection
  │   └ bounding volume hierarchy
  └ narrow-phase collision detection
      ├ bounding volume: sphere/AABB/OBB
      └ body: ball/box/polygon

本文自底向上介紹。

collision / intersection

碰撞。兩個形狀，相互接觸，止於形狀邊界。物理學詞彙。

相交。兩個形狀，相互重疊，可以深入形狀內部。數學詞彙。

電腦做計算，一切皆數學。雖然章節標題是碰撞，但是章節內容是相交。

closest pair / shortest distance

沒有碰撞的時候，我們討論最近點對、最短距離。

最近點對：兩個形狀，以最短直線相連，端點位置。

最短距離：兩個形狀，以最短直線相連，線條長度。

碰撞偵測演算法，稍作修改即可計算最近點對、最短距離。

contact / penetration depth

發生碰撞的時候，我們討論接觸位置、侵入深度。

二維接觸方式：點點、點邊、邊點、邊邊。四種。

三維接觸方式：點邊面排列。九種。

兩個形狀互相重疊，需要追溯接觸位置、估計侵入深度。

簡易算法：窮舉兩個形狀的每一個表面。沿著法向量方向，將另個形狀挪至表面，當作接觸位置。挪動距離，當作侵入深度。從中選擇挪動距離最少者。

複雜算法，此處省略。例如交點連線的垂直方向。例如轉動。

碰撞偵測演算法，稍作修改即可計算接觸位置、侵入深度。

ball–ball collision
（circle collision / sphere collision）

二維圓形碰撞、三維球體碰撞。O(1)。

圓心距≤半徑和。

box–box collision
（rectangle collision / cuboid collision）

二維長方形碰撞、三維長方體碰撞。O(1)。

自己中央到他人頂點的距離≤半寬（半高）。

Box2D-lite的實作非常漂亮，值得一看。

一、演算法：separating axis theorem (SAT)。

二、依序處理兩個矩形，分別作為基準。

三、基準矩形，旋轉擺正，方便計算水平距離（垂直距離）。

四，另個矩形，四個頂點向量(±w/2, ±h/2)隨之旋轉。我們只需要X座標極值（Y座標極值）。旋轉矩陣取絕對值，簡化計算。

ball–box collision
（circle–rectangle collision / sphere–cuboid collision）

二維圓矩碰撞、三維球箱碰撞。O(1)。

圓心到矩邊的最短距離≤半徑。

convex polygon collision

二維凸多邊形碰撞。O(N)。

樸素算法：簡化為線段碰撞。枚舉各種線段配對，偵測是否碰撞。O(N²)。

不知名算法：所有邊，依照角度排序，依序檢查。O(N)。

兩個凸多邊形的交集，仍是凸多邊形。兩個凸多邊形的所有邊，涵蓋了交集的所有邊。保留交集的邊，捨棄其餘的邊。

一個凸多邊形的所有邊，恰好依照角度排序。實施merge sort，合併兩個凸多邊形的所有邊，依照角度排序。

依序掃描所有邊，每當凸多邊形更替，就偵測前邊與後邊是否碰撞。若碰撞，後邊是交集，保留；若無碰撞，後邊不是交集，捨棄。

上述過程是multi-pass。亦可改成one-pass，一邊合併、一邊偵測碰撞。

convex polyhedron collision

三維凸多面體碰撞。O(N²)。

樸素算法：簡化為三角形碰撞。枚舉各種三角形配對，偵測是否碰撞。O(N²)。

separating axis theorem (SAT)：三角形碰撞改成影子碰撞。叉積改成點積，節省時間。

Gilbert–Johnson–Keerthi algorithm (GJK)：枚舉順序，朝向交集。以此減少枚舉數量，進一步節省時間。

SAT可以平行計算，GJK無法平行計算。目前主流是SAT。

convex polyhedron collision:
separating axis theorem

【三維SAT實在太難作圖。姑且用二維SAT應付一下。】

一、首先介紹影子。

三角形視作牆壁。另一個三角形視作飛鏢。碰撞視作飛鏢穿牆。

三角形頂點，投影到牆壁法向量，偵測影子碰撞。

藉由投影，計算三角形頂點到牆壁延伸面的距離。距離為正值，影子無碰撞；距離為負值，影子有碰撞。

二、三角形碰撞、影子碰撞，兩者不等價。

三角形為主角：
一、三角形碰撞，保證影子碰撞。
二、三角形無碰撞，不保證影子有無碰撞。
影子為主角：
三、影子碰撞，不保證三角形有無碰撞。
四、影子無碰撞，保證三角形無碰撞。

此演算法以影子為主角。因此採用第四個性質：影子無碰撞。

三、偵測影子無碰撞。

凸多面體A，每一個面分別作為牆壁。

凸多面體A與B，每一個點皆投影到牆壁法向量。

法向量朝外視作正向。投影處越外視作越高。A中最高點低於B中最低點，或者，B中最高點低於A中最低點。

四、援引hyperplane separation theorem。

兩個凸的形狀，能以任意平面隔開，即無碰撞。

一旦影子無碰撞，立即結束演算法，節省時間。

五、最短距離、侵入深度。

影子距離就是垂直距離。隨時紀錄最小值。

convex polyhedron collision:
Gilbert–Johnson–Keerthi algorithm

一、首先介紹Minkowski difference。

形狀A、形狀B，兩者的Minkowski difference，是形狀C。

A中一點，B中一點，兩者座標相減，得到C中一點。

A中一點，B中一點，枚舉各種配對，得到整個形狀。

二、如何利用Minkowski difference偵測碰撞呢？

兩個凸多面體的Minkowski difference，恰是一個凸多面體。

證明很簡單。凸的定義，寫成數學式子，相減一下就行了。

兩個凸多面體碰撞，那麼Minkowski difference包含原點。沒有碰撞，那麼不含原點。

證明很簡單。交點，座標相減是0。無交點，座標相減非0。

最後得到一個碰撞偵測演算法：先計算Minkowski difference，再判斷是否包含原點。

三、如何找出Minkowski difference，並且偵測碰撞呢？

樸素算法：求出整個Minkowski difference。

取巧算法：求出部分Minkowski difference，節省時間。

一邊建立四面體剖分，一邊移動至相鄰四面體。逐步靠近原點。

首先求出任意四個頂點，形成四面體。每回合找到一個新頂點，並且移動至相鄰四面體。逐步靠近原點。

Minkowski difference恰是凸的，四面體剖分恰是連通的，得以使用貪心法。只要逐步靠近原點，終會抵達最近之處。

補充說明一下。二維的情況下，移動過程可以視作Minkowski difference所有頂點實施binary search，找到最靠近原點的頂點。

所有頂點形成一條鏈。每回合找到一個新頂點，將鏈截成兩段，並且保留靠近原點的那一段。兩條鏈並未均分，最多N回合。

四、如何找出Minkowski difference的新頂點呢？

找出一個朝向原點的方向向量。A中最高點、B中最低點，兩者相減，得到Minkowski difference的新頂點。

這宛如SAT。本來枚舉A的面，現在枚舉A與B的頂點。本來使用法向量，現在使用朝向交集的方向向量。由於走向原點，只需枚舉部分頂點，不需枚舉所有面，節省時間。

還可以順手偵測影子無碰撞，立即結束演算法。由於走向一致，只需檢查A中最高點低於B中最低點，不需檢查B中最高點低於A中最低點，又節省一半時間。

五、如何找出朝向原點的方向向量，進而求得新頂點呢？

求第一頂點：使用任意方向向量。例如X軸方向。

求第二頂點：使用反方向。

求第三頂點：兩頂點形成線段。再與原點形成三角形。三角形法向量、線段向量，兩者叉積，得到朝向原點的向量。

求第四頂點：三頂點形成三角形。三角形法向量，正向與反向，找出朝向原點者。

求後續各頂點：四頂點形成四面體。三個新三角形、一個舊三角形。三個新三角形法向量，找出朝向原點者。任一皆可。

六、如何計算最短距離呢？

兩個凸多面體的最短距離，即是Minkowski difference與原點的最短距離。

四面體的移動過程當中，隨時計算四面體與原點的最短距離。

但是無法計算侵入深度！包含原點的四面體，通常不是距離最近的面。

七、如何計算侵入深度呢？

樸素算法：求出整個Minkowski difference，枚舉每個面。

取巧算法：求出部分Minkowski difference，節省時間。

GJK的變種expanding polytope algorithm。

包含原點的四面體，不斷併入相鄰四面體，擴展成更大的凸多面體。原點到面的距離，小於當前侵入深度，那麼併入該面暨外側任一頂點所形成的四面體。大於等於當前侵入深度，那麼該面外側距離更遠，不必擴展。

運氣最差時，可能擴展成整個Minkowski difference。

八、如何減少數值誤差呢？

GJK的變種Minkowski portal refinement。

四面體的其中一個頂點，保持在凸多面體的中心。

優點是四面體不會太扁，得以減少數值誤差。優點是容易計算最短距離。仍然無法計算侵入深度。

farthest point in a direction

SAT和GJK都用到了「給定一個方向向量，找到凸多面體中的最高點」。

樸素算法：凸多面體的所有點，投影到方向向量，得到投影量，取最大值。O(N)。

凸多邊形：預先切成上鏈與下鏈。兩鏈都是單峰函數，無論方向向量為何。兩鏈分別實施bisection method求得極值，其中一個極值是最大值。O(logN)。

凸多面體：預先切成上殼與下殼。兩殼都是單峰函數，無論方向向量為何。使用quadtree儲存頂點，方便實施bisection method。O(N)。

simple polygon collision

二維簡單多邊形碰撞。O(NlogN)。

Shamos–Hoey algorithm：直接視作大量線段相交問題，直接使用其演算法。平移的掃描線，輔以二元搜尋樹。

simple polyhedron collision

三維簡單多面體碰撞，好像是O(N²)。

Lin–Canny algorithm：我沒有研究。

V-Clip：我沒有研究。

narrow-phase collision detection

兩個物體碰撞偵測。

根據物體形狀，有著各種演算法，請見前面小節。

凸多面體有高速演算法。大家把一個簡單多面體切割成多個凸多面體，以便降低計算時間。我沒有研究。我猜測是四面體剖分。

bounding volume

兩個物體碰撞偵測，先以外框初步篩檢。

物體實施SAT或CJK偵測碰撞，O(N)。

替物體設計簡易外框，得以迅速偵測碰撞，O(1)。

外框沒有碰撞，保證物體沒有碰撞，大可不必實施SAT或CJK。外框有碰撞，才進一步實施SAT或CJK，偵測物體是否碰撞。

外框偵測碰撞，些微增加時間；物體偵測碰撞，大幅減少時間。剛體模擬過程，少數時候才有碰撞，多數時候沒有碰撞。利大於弊。

外框造型有三種：

bounding sphere：體積最小的球。平均O(N)。

bounding box：體積最小的長方體，細分為AABB和OBB。

axis-aligned bounding box (AABB)：必須擺正。O(N)。

oriented bounding box (OBB)：不必擺正。二維O(NlogN)。三維O(N³)。

建立外框的演算法，另以專門頁面介紹。

OBB節省最多偵測時間。貼合物體，減少誤判。

OBB耗費最多建立時間。所幸剛體不會變形，得以預先計算。

broad-phase collision detection

大量物體碰撞偵測，先以佔位範圍初步篩檢。

發明特殊資料結構，儲存所有物體的佔位範圍。

樸素算法：枚舉所有物體配對。O(N²)。N是物體數量。

uniform grid：計算每個物體的bounding sphere。找出直徑的最大值。建立網狀方格，格子寬度是直徑。每當發生碰撞，物體一定位在相同格子或相鄰格子。實施bucket sort，所有物體存入對應格子。建立O(N+Kᴰ)，偵測至少是O(N3ᴰ)。

quadtree / octree：當相同區域有多個物體，就遞迴分割區域，直到每個區域只有一個物體。首先（由葉往根）逐步擴張區域，直到不可能發生碰撞。然後（由根往葉）檢查轄下所有區域所有物體。時間複雜度尚待確認。

bounding region hierarchy / bounding volume hierarchy：計算每個物體的AABB。外框依照物體位置排序。相鄰兩個外框不斷併成一個外框，形成二元樹。（由根往葉）先檢查大外框碰撞，再檢查小外框碰撞。建立O(DNlogN)，偵測至少是O(NlogN)。

區域資料結構，另以專門頁面介紹。

當物體座標隨時改變，要嘛每次重新建立資料結構，要嘛使用動態資料結構。我沒有研究。

discrete collision detection

Δt是定值。先套用Δt求得物體位置，再追溯接觸位置。

continuous collision detection

Δt不是定值。先求得Δt與接觸位置，再更新物體位置。

UVa 11574

架構

motion
├ translational motion / rotational motion
├ linear motion / nonlinear motion / circular motion
└ spin motion / orbital motion

motion

數學幾何變換有三個因素：平移、旋轉、縮放。

物理運動有兩個因素：平移運動（移動）、旋轉運動（轉動）。

（縮放運動沒有特地命名。詳情請見柔體模擬章節。）

translational motion / rotational motion

平移運動（移動）、旋轉運動（轉動），各有一套物理量。

物理量有四類：位置變化、運動量、運動量變化、運動量差異。

平移運動（移動）的物理量：

name                 | notation        丨中文　　丨意義
---------------------|-----------------丨一一一一丨一一一一
position             | s               丨位置　　丨　
velocity             | v = ds/dt       丨速度　　丨位置變化
acceleration         | a = dv/dt       丨加速度　丨速度變化
---------------------|-----------------丨一一一一丨一一一一
mass                 | m               丨質量　　丨平移慣量
momentum             | p = mv          丨動量　　丨平移動量
energy               | E = ½mv²        丨能量　　丨平移能量
---------------------|-----------------丨一一一一丨一一一一
mass flow rate       | ṁ = dm/dt       丨質量流量丨質量變化
force                | F = dp/dt = ma  丨力　　　丨動量變化
power                | P = dE/dt = F∙v 丨功率　　丨能量變化
---------------------|-----------------丨一一一一丨一一一一
                     |                 丨　　　　丨質量差異
impulse              | J = ∫ F dt      丨衝量　　丨動量差異
work                 | W = ∫ᴄ F∙ds     丨功　　　丨能量差異

旋轉運動（轉動）的物理量：

angular position     | θ               丨角位置　丨　
angular velocity     | ω = dθ/dt       丨角速度　丨位置變化
angular acceleration | α = dω/dt       丨角加速度丨速度變化
---------------------|-----------------丨一一一一丨一一一一
moment of inertia    | I               丨慣性矩　丨旋轉慣量
angular momentum     | L = Iω          丨角動量　丨旋轉動量
rotational energy    | T = ½Iω²        丨旋轉能量丨旋轉能量
---------------------|-----------------丨一一一一丨一一一一
                     | İ = dI/dt       丨　　　　丨慣量變化
torque               | τ = dL/dt = Iα  丨力矩　　丨動量變化
rotational power     | P = dT/dt = τ∙ω 丨旋轉功率丨能量變化
---------------------|-----------------丨一一一一丨一一一一
                     |                 丨　　　　丨質量差異
angular impulse      | J = ∫ τ dt      丨角衝量　丨動量差異
rotational work      | W = ∫ᴄ τ∙dθ     丨旋轉功　丨能量差異

vector

物理學家發現，運動可以合成和拆解。

為了表達合成和拆解，物理學家發明了向量。

拆解時，令分量互相垂直，方便計算。

平移運動（移動）的物理量，皆是純量。拆解成三份物理量，對應三個方向XYZ，形成向量。得以描述平移方向。

旋轉運動（轉動）的物理量，皆是純量。拆解成三份物理量，對應三種轉軸XYZ，形成向量。得以描述旋轉方向。

【註：此處是同步旋轉三個角度；Euler angles是依序旋轉三個角度。旋轉一段時間Δt，同步旋轉和依序旋轉的結果不同；旋轉極短時間dt，兩者才相同。旋轉位置不適合拆成三份物理量；旋轉速度才適合拆成三份物理量，並且等同於Euler angles。物理教科書總是直接介紹Euler angles，而不介紹同步和依序的差別。】

利用三角函數（點積），將純量變成三份物理量（向量）。利用勾股定理（範數），將三份物理量（向量）變成純量。

平移運動（移動）的物理量，延伸內容：

displacement         | Δs = s' - s     丨位移　　丨位置差異（向量）
distance             | ‖Δs‖            丨距離　　丨位置差異（純量）
---------------------|-----------------丨一一一一丨一一一一一一一一
velocity             | v = ds/dt       丨速度　　丨位置變化（向量）
speed                | ‖v‖             丨速率　　丨位置變化（純量）

旋轉運動（轉動）的物理量，延伸內容：

angular displacement | Δθ = θ' - θ     丨角位移　丨位置差異（向量）
angular distance     | ‖Δθ‖            丨角距離　丨位置差異（純量）
---------------------|-----------------丨一一一一丨一一一一一一一一
angular velocity     | ω = dθ/dt       丨角速度　丨位置變化（向量）
angular speed        | ‖ω‖             丨角速率　丨位置變化（純量）

linear motion / non-linear motion

數學幾何變換，只考慮起點終點，不考慮軌跡。

物理運動，需要考慮軌跡。

移動分為直線運動和曲線運動，在空間中產生直線軌跡和曲線軌跡。

轉動分為直線運動和曲線運動，在球面上產生直線軌跡與曲線軌跡。

circular motion

圓周運動。產生圓形軌跡。屬於曲線運動。

物理教科書只介紹移動之圓周運動，沒有介紹轉動之圓周運動。大家提到圓周運動，心裡預設為移動。

spin motion（rotation around a fixed axis）

自旋運動。質點繞著轉軸移動。物體繞著轉軸轉動。

許多個圓形軌道運動，堆疊起來。旋轉中心，連成一線。

spin motion公式清單（純量版本）

接下來介紹圓形軌道運動的計算技巧。

文言文：質點移動之圓周運動、物體轉動之直線運動，兩者的物理量可以互相轉換！白話文：圓形移動視作直線轉動，方便計算。

              | translational    | rotational      |
   spin       | motion           | motion          |
   motion     | with circular    | with linear     |
  (scalar)    | trajectory       | trajectory      |
--------------|------------------------------------|
radius        | r                                  | 半徑
--------------|------------------------------------|
position      | s = θr           | θ = s/r         | 位置
velocity      | v = ωr           | ω = v/r         | 速度
acceleration  | a = αr           | α = a/r         | 加速度
--------------|------------------|-----------------|
inertia       | m        = I/r²  | I        = mr²  | 慣量
momentum      | p = mv   = L/r   | L = Iω   = pr   | 動量
energy        | E = ½mv² = T     | T = ½Iω² = E    | 能量
--------------|------------------|-----------------|
force/torque  | F = ma   = τ/r   | τ = Iα   = Fr   | 力／力矩
--------------|------------------------------------|
centripetal   | ac = v²/r = ω²r                    | 向心加速度
 acceleration |                                    |
centripetal   | Fc = mac                           | 向心力
 force        |                                    |

上述轉換公式，符號都是純量。

spin motion公式重點（純量版本）

┌─────────┐   ┌─────────┐┌─────────┐
│   L/r   │ = │   I/r²  ││   ω r   │
└─────────┘   └─────────┘└─────────┘
     p             m          v

┌─────────┐   ┌─────────┐┌─────────┐
│   p r   │ = │   m r²  ││   v/r   │
└─────────┘   └─────────┘└─────────┘
     L             I          ω

spin motion公式推導過程（純量版本）

位置。根據角度的定義，得到s/r = θ。

速度。相同角速度，半徑越大、弧線越長、平移越遠、速度越快。得到v = ωr。

動量。半徑越大，弧線越長。必須更加強勁，才能達到相同角速度。得到pr = L。

慣量。動量p=mv、角動量L=Iω。乘以r、除以r，等號兩邊一樣多r。得到I = mr²。

延伸閱讀：moment

物體處處有質點。累計所有質點，得到平移運動量。同時考慮半徑r，得到旋轉運動量。為了表達旋轉運動量，物理學家發明了矩。

矩的定義：uₙ = ∫ q(r) rⁿ dr。旋轉慣量（慣量矩）L = pr，旋轉動量（角動量）I = mr²，都是矩。

spin motion的慣量（純量版本）

平移運動的慣量，稱作「平移慣量」或「質量」。

自旋運動的慣量，稱作「旋轉慣量」或「慣性矩」。

平移慣量取決於物體質地。它是一個數值，實際測量而得。

旋轉慣量取決於物體質地、物體造型、旋轉中心。需要計算。

一個質點的旋轉慣量：質點與旋轉中心的距離平方，乘以質量。

一個物體的旋轉慣量：每個質點分別計算旋轉慣量，通通加總。

維基百科整理了一份列表。有些圖片忘記畫出轉軸。

一個物體的旋轉慣量，可以視作函數。函數輸入是旋轉中心，函數輸出是旋轉慣量，函數本身是上述計算公式。

spin motion公式清單（向量版本）

每個質點的旋轉中心，位於轉軸各處，難以計算半徑。

物理學家利用叉積，簡化計算過程，不需刻意計算半徑。

原點設定成轉軸上面任意一點，半徑向量設定成質點座標，以此建立數學公式。

然而為了建立叉積反運算，還是需要刻意計算半徑向量。

模仿純量版本的數學公式，迎合叉積運算的右手定則，導致向量方向相當詭異。習慣就好了：

純量版本：角位置、角速度、角加速度，朝向旋轉方向。

向量版本：角位置、角速度、角加速度，朝向轉軸方向（旋轉平面的法向量）。半徑向量，遠離旋轉中心（圓形軌道的法向量）。

              | translational    | rotational      |
    spin      | motion           | motion          |
    motion    | with circular    | with linear     |
   (vector)   | trajectory       | trajectory      |
--------------|------------------------------------|
radius vector | r                                  | 半徑向量
--------------|------------------------------------|
position      | s = θ×r          | θ = r⁻¹×s       | 位置
velocity      | v = ω×r          | ω = r⁻¹×v       | 速度
acceleration  | a = α×r          | α = r⁻¹×a       | 加速度
--------------|------------------|-----------------|
inertia       | m        = Ir⁻²  | I         = mr² | 慣量
momentum      | p = mv   = L×r⁻¹ | L = Iω    = r×p | 動量
energy        | E = ½mv² = T     | T = ½ωᵀIω = E   | 能量
--------------|------------------|-----------------|
force/torque  | F = ma   = τ×r⁻¹ | τ = Iα    = r×F | 力／力矩
--------------|------------------------------------|
centripetal   | ac = r⁻¹×v×v = ω×(ω×r)             | 向心加速度
 acceleration |                                    |
centripetal   | Fc = mac                           | 向心力
 force        |                                    |

r   = [x y z]ᵀ     (x,y,z) is coordinates of r
r⁻¹ = r/‖r‖²       ‖r‖ is length of r
r²  = RR           R is cross product matrix of r
r⁻² = (RR)⁻¹       (RR)⁻¹ is inverse matrix of RR【尚待確認】
                   (then reduce diagonal matrix to scalar)

上述轉換公式，符號都是向量。除了慣量、能量、r²、r⁻²。

spin motion公式重點（向量版本）

┌─────────┐   ┌─────────┐┌─────────┐
│  L×r⁻¹  │ = │   Ir⁻²  ││   ω×r   │
└─────────┘   └─────────┘└─────────┘
     p             m          v

┌─────────┐   ┌─────────┐┌─────────┐
│   r×p   │ = │   mr²   ││  r⁻¹×v  │
└─────────┘   └─────────┘└─────────┘
     L             I          ω

spin motion公式推導過程（向量版本）

省略。我是看這本書：

《Introduction to Classical Mechanics》，作者Atam Arya。

spin motion的慣量（向量版本）

I從純量改成了張量，尺寸3×3。

一個質點的旋轉慣量：請見下述數學公式。最後得到矩陣。

    ⎡ Iₓₓ Iₓ₝ Iₓ₞ ⎤
I = ⎢ I₝ₓ I₝₝ I₝₞ ⎥   moment of inertia tensor
    ⎣ I₞ₓ I₞₝ I₞₞ ⎦

Iₓₓ = m(y² + z²) =  m(‖r‖² - x²)
I₝₝ = m(x² + z²) =  m(‖r‖² - y²)
I₞₞ = m(x² + y²) =  m(‖r‖² - z²)
Iₓ₝ = I₝ₓ = mxy
I₝₞ = I₞₝ = mzy
I₞ₓ = Iₓ₞ = mxz

    ⎡x⎤
r = ⎢y⎥   radius vector
    ⎣z⎦

‖r‖² = x² + y² + z²

慣量公式推導過程。

L = r × p             1 particle
  = r × (mv)
  = m (r × v)
  = m (r × (ω × r))
  = -m (r × (r × ω))
  = -mRRω
       ⎡  0 -z  y ⎤ ⎡  0 -z  y ⎤ ⎡ωₓ⎤
  = -m ⎢  z  0 -x ⎥ ⎢  z  0 -x ⎥ ⎢ω₝⎥
       ⎣ -y  x  0 ⎦ ⎣ -y  x  0 ⎦ ⎣ω₞⎦
       ⎡ -y²-z²   xy     xz   ⎤ ⎡ωₓ⎤
  = -m ⎢   xy   -x²-z²   yz   ⎥ ⎢ω₝⎥
       ⎣   xz     yz   -x²-y² ⎦ ⎣ω₞⎦
    ⎡ my²+mz²  -mxy    -mxz   ⎤ ⎡ωₓ⎤
  = ⎢  -mxy   mx²+mz²  -myz   ⎥ ⎢ω₝⎥
    ⎣  -mxz    -myz   mx²+my² ⎦ ⎣ω₞⎦

let L = Iω
         ⎡ my²+mz²  -mxy    -mxz   ⎤
thus I = ⎢  -mxy   mx²+mz²  -myz   ⎥
         ⎣  -mxz    -myz   mx²+my² ⎦

    ⎡  0 -z  y ⎤
R = ⎢  z  0 -x ⎥   cross product matrix
    ⎣ -y  x  0 ⎦

一個物體的旋轉慣量：每個質點分別計算旋轉慣量，加總矩陣。

L = ∑ (rᵢ × pᵢ)      all particles of a body
  = ∑ -mᵢRᵢRᵢωᵢ
  = (∑ -mᵢRᵢRᵢ)ω     (1)
  = m(∑ -RᵢRᵢ)ω      (2)

let L = Iω
thus I = m (∑ -RᵢRᵢ)
           ⎡ ∑(yᵢ²+zᵢ²)   -∑xᵢyᵢ     -∑xᵢzᵢ   ⎤
       = m ⎢   -∑xᵢyᵢ   ∑(xᵢ²+zᵢ²)   -∑yᵢzᵢ   ⎥
           ⎣   -∑xᵢzᵢ     -∑yᵢzᵢ   ∑(xᵢ²+yᵢ²) ⎦

(1) all particles of a body
    have same angular velocity ω₁ = ω₂ = ...
    and let ω = ωᵢ

(2) assume all particles of a body
    have same mass m₁ = m₂ = ...
    and let m = ∑mᵢ

orbital motion（translation around a fixed point）

軌道運動。質點繞著中心移動。物體繞著中心轉動。

當旋轉中心是固定的（球心），當質點與旋轉中心的距離是固定的（半徑），當軌跡位於平面，則形成圓形軌道運動。

orbital motion的慣量

軌道運動（旋轉運動）如何定義慣量？我不知道。

一種方式：旋轉運動是「轉軸隨時變動的自旋運動」。針對當前時刻的轉軸，求得旋轉慣量。

另一種方式tennis racket theorem：旋轉運動是「三個自旋運動同步進行」。針對三個轉軸，分別求得三個旋轉慣量。轉軸固定在物體上面，三個旋轉慣量保持不變。

架構

rigid body motion
├ rigid body
├ rigid body motion
├ rigid body contact force
└ rigid body collision

rigid body

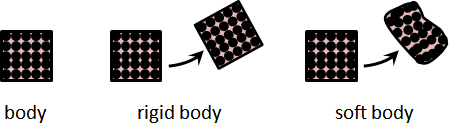
質點。一份物質，只考慮慣量，不考慮體積。

物體。質點連成一串、連成一片、連成一團，形成特定形狀。

剛體。質點距離固定不變，無論如何運動。

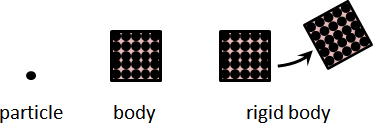
地球不存在質點、物體、剛體。它們只是特殊的數學模型，用於描述特殊的物理現象。

物理學家發明質點、物體、剛體，意在長話短說、講重點。要是從原子、化學鍵、晶體結構開始講起，太過複雜、講不清楚。

rigid body motion

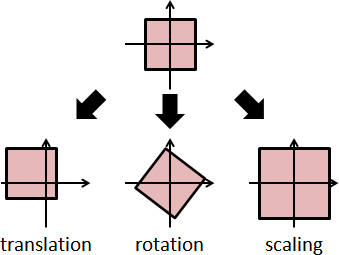
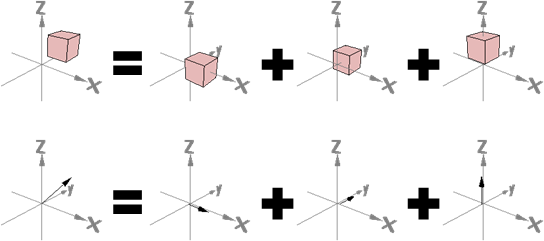
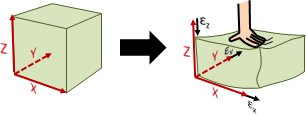
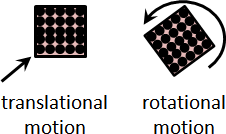
質點運動只能移動。剛體運動只能移動和轉動。

地球不存在質點運動、剛體運動。它們只是模仿了數學的剛體變換。

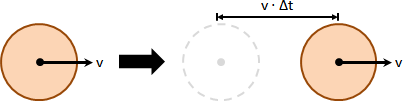
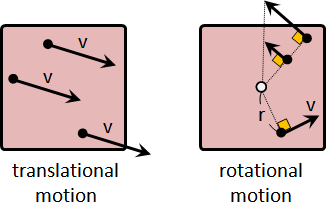
translational motion
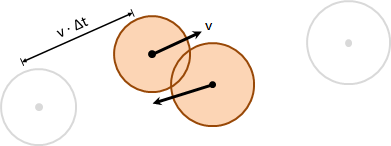
rotational motion

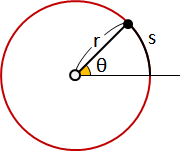
平移運動（移動）：速度大小、速度方向，每個質點全部一致。

旋轉運動（轉動）：速度大小正比於半徑大小。速度方向垂直於半徑方向。

剛體轉動，其質點不會轉動。否則物體就散架了。

剛體轉動，其質點只會移動。軌跡是圓形。

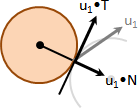
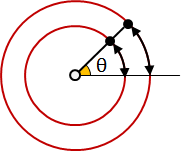
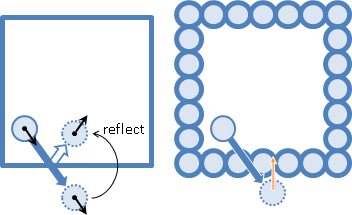
instantaneous center of rotation
instantaneous axis of rotation

剛體轉動過程當中，速度是零的位置。可能在物體外部。

旋轉中心（瞬心）：二維轉動的情況下，形成一個點。

轉軸（瞬軸）：三維轉動的情況下，形成一條線。

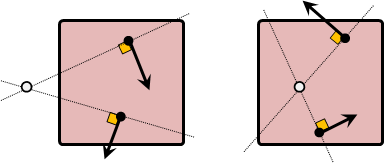
二維轉動，給定兩點速度，可以推導旋轉中心。速度垂線交點。

三維轉動，給定兩點速度，可以推導轉軸。速度垂面交線。

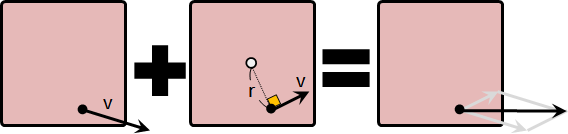
combined translational and rotational motion

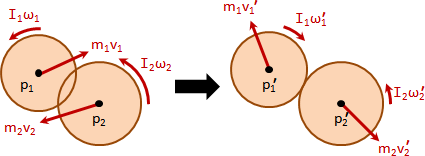
剛體的每個質點各自擁有速度。

又移動又轉動，質點速度是兩者速度相加。

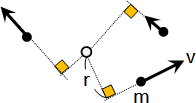
二維的情況下，又移動又轉動，等同於不移動只轉動。旋轉中心改變了。

三維的情況下，又移動又轉動，等同於又沿轉軸移動、又繞轉軸轉動。轉軸改變了。

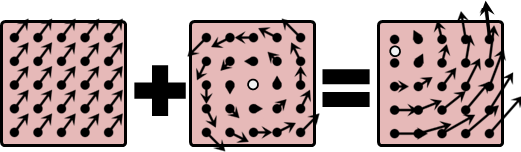
translational momentum of rotational motion

剛體的每個質點各自擁有速度。

平移運動：質點速度一致。平移動量總和顯而易見。

旋轉運動：當物體均勻對稱，而且旋轉中心是對稱中心，平移動量總和才是零。否則平移動量總和通常不是零。甚至每個時刻的平移動量總和，方向都不同。

又移動又轉動，平移動量守恆，那麼運動軌跡為何？我不知道。

平移速度可以納入旋轉速度。那麼平移動量可以納入旋轉動量嗎？平移慣量可以納入旋轉慣量嗎？我不知道。

translational inerita（mass）

剛體可以定義平移慣量（質量）。以下是推導過程。

剛體平移速度＝質點平移速度。依據是質點距離固定不變、質點速度均等。

v = vᵢ for all i

v = v₁ = v₂ = ...

剛體平移動量＝質點平移動量總和。稱作動量守恆定律law of momentum conservation。

p = ∑ mᵢvᵢ

p = m₁v₁ + m₂v₂ + ...

剛體平移慣量＝質點平移慣量總和。依據是數學分配律。

m = ∑ mᵢ

p = m₁v₁ + m₂v₂ + ...
  = m₁v + m₂v + ...
  = (m₁ + m₂ + ...)v

let p = mv
thus m = m₁ + m₂ + ...   when v ≠ 0

剛體可以視作大量質點。剛體平移慣量＝質點平移慣量總和。剛體平移動量＝質點平移動量總和。剛體平移動量變化＝質點平移動量變化總和。旋轉亦然。

rotational inertia（moment of inertia）

剛體可以定義旋轉慣量（慣性矩）。推導過程如法炮製。

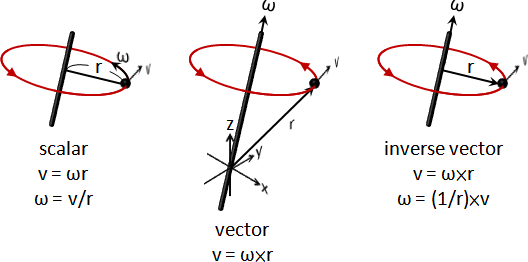
剛體旋轉速度＝質點圓周運動平移速度。依據是spin motion轉換公式。

ω = ωᵢ for all i

剛體旋轉動量＝質點圓周運動平移動量總和。依據是動量守恆定律law of momentum conservation。

L = ∑ Iᵢωᵢ

剛體旋轉慣量＝質點旋轉慣量總和。依據是數學分配律。

I = ∑ Iᵢ

剛體旋轉半徑＝質點旋轉半徑方均根。稱作迴轉半徑radius of gyration。簡稱gyradius。

r_gy = √∑ rᵢ² / n

I = ∑ Iᵢ
m rgy² = ∑ mᵢrᵢ²
m rgy² = ∑ (m/n)rᵢ²
  rgy² = ∑ (1/n)rᵢ²
  rgy  = √∑ rᵢ² / n

注意到，雖然命名為旋轉，但是其實是自旋。成為歷史共業。

translational inertia（mass）
rotational inertia（moment of inertia）

平移運動、旋轉運動，各自擁有慣量。

平移慣量（質量）：一個數值，實際測量而得。m。

旋轉慣量（慣量矩）：一個數值（純量版本）或者一個矩陣（向量版本），利用微積分推導而得。I。

首先確認旋轉中心，以便得到旋轉半徑。平移慣量乘以旋轉半徑平方，累計每個質點。令質點無限微小，對質點積分。

translational momentum（linear momentum）
rotational momentum（angular momentum）

平移運動、旋轉運動，各自擁有動量。

平移動量（線動量）：平移慣量乘以平移速度。p=mv。

旋轉動量（角動量）：旋轉慣量乘以旋轉速度。L=Iω。

上述數學公式，可以引入半徑r，藉由spin motion。

兩者皆是純量，可以推廣成向量，藉由叉積。

旋轉動量（線動量）：p=mv推廣成p=L×(1/r)。

平移動量（角動量）：L=Iω推廣成L=r×p。

translational force（force）
rotational force（torque）

平移力（力）：平移動量變化快慢。F=dp/dt。

旋轉力（力矩）：旋轉動量變化快慢。T=dL/dt。

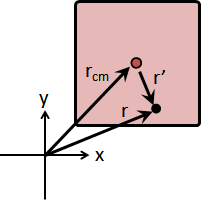
center of mass

剛體可以定義質心。

質心位置。質點位置的加權平均數，權重是平移慣量（質量）。

r_cm = (∑ mᵢrᵢ) / (∑ mᵢ)

質心速度。質心位置變化快慢。

v_cm = d/dt r_cm

質心的主要用途是建立數學公式。推導過程源自這本書籍。

剛體質點位置。拆成兩項，質心位置與相對位置。

r = r_cm + r̃

剛體質點速度。拆成兩項，質心速度與相對速度。

v = v_cm + ṽ

vᵢ = d/dt rᵢ
   = d/dt (rcm + r̃ᵢ)
   = (d/dt rcm) + (d/dt r̃ᵢ)
   = vcm + ṽᵢ

大量質點旋轉慣量（當旋轉中心位於原點）。拆成兩項，軌道慣量與自旋慣量（公轉與自轉）。

I = I_cm + ∑ mᵢr̃ᵢ²

I = ∑ mᵢrᵢ²
  = ∑ mᵢ(rcm + r̃ᵢ)²
  = ∑ mᵢ(rcm² + r̃ᵢ² + 2 rcmr̃ᵢ)
  = (∑ mᵢrcm²) + (∑ mᵢr̃ᵢ²) + (∑ mᵢ 2 rcmr̃ᵢ)
     ^^^^^^^^     ^^^^^^^     ^^^^^^^^^^^^
   Iorbit = Icm    Ispin           0

Iorbit = ∑ mᵢrcm²
       = rcm² (∑ mᵢ)
       = rcm² m
       = mrcm²

Ispin = ∑ mᵢr̃ᵢ²

rcm = (∑ mᵢrᵢ) / (∑ mᵢ)

∑ mᵢr̃ᵢ = ∑ mᵢ(rcm - rᵢ)
       = (∑ mᵢ rcm) - ∑ mᵢrᵢ
       = (rcm ∑ mᵢ) - ∑ mᵢrᵢ
       = ∑ mᵢrᵢ - ∑ mᵢrᵢ
       = 0

∑ mᵢ 2 rcmr̃ᵢ = 2 rcm (∑ mᵢr̃ᵢ)
             = 0

剛體旋轉慣量（當轉軸穿過原點）。拆成兩項，軌道慣量與自旋慣量（公轉與自轉）。稱作平行軸定理parallel axis theorem。

旋轉中心改成轉軸，否則物體就散架了。半徑向量投影到轉軸的垂面。

半徑向量再改成質心與轉軸的距離d，導致數學式子每個變數都是相對位置，大可不必在意轉軸是否穿過原點。

數學符號標記方式截然不同，請務必小心。

I = md² + I_cm

I = ∑ mᵢrᵢ²               -->   I = ∑ mᵢdᵢ²
  = (mrcm²) + (∑ mᵢr̃ᵢ²)           = md² + (∑ mᵢd̃ᵢ²)

I = (mrcm²) + (∑ mᵢr̃ᵢ²)
     ^^^^^     ^^^^^^^
      md²        Icm   wikipedia and textbooks

大量質點旋轉動量（當旋轉中心位於原點）。拆成兩項，軌道動量與自旋動量（公轉與自轉）。

L = L_cm + ∑ r̃ᵢ × mᵢṽᵢ

L = ∑ rᵢ × mᵢvᵢ
  = ∑ (rcm + r̃ᵢ) × mᵢvᵢ
  = (∑ rcm × mᵢvᵢ) + (∑ r̃ᵢ × mᵢvᵢ)
    ^^^^^^^^^^^^^^   ^^^^^^^^^^^^^^
     Lorbit = Lcm        Lspin

Lorbit = ∑ rcm × mᵢvᵢ
       = rcm × (∑ mᵢvᵢ)
       = rcm × p

Lspin = ∑ r̃ᵢ × mᵢvᵢ
      = ∑ r̃ᵢ × mᵢ(vcm + ṽᵢ)
      = ∑ r̃ᵢ × (mᵢvcm + mᵢṽᵢ)
      = (∑ r̃ᵢ × mᵢvcm) + (∑ r̃ᵢ × mᵢṽᵢ)
      =        0       + (∑ r̃ᵢ × mᵢṽᵢ)
      = ∑ r̃ᵢ × mᵢṽᵢ

∑ mᵢr̃ᵢ = 0

∑ r̃ᵢ × mᵢvcm = ∑ mᵢr̃ᵢ × vcm
             = ∑ -vcm × mᵢr̃ᵢ
             = -vcm × ∑ mᵢr̃ᵢ
             = 0

剛體旋轉動量（當轉軸穿過原點）。拆成兩項，軌道動量與自旋動量（公轉與自轉）。稱作König's theorem。

L = d × p + L_cm

如法炮製

這些數學公式其實只是拆出一個常數項。這個手法也出現在機率論的期望值、變異數公式。

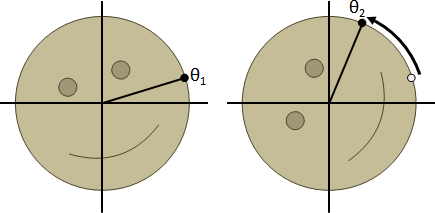
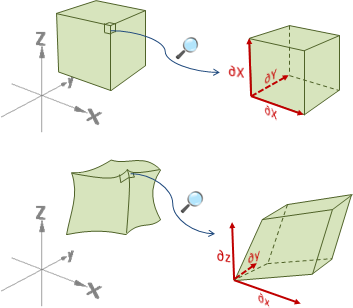
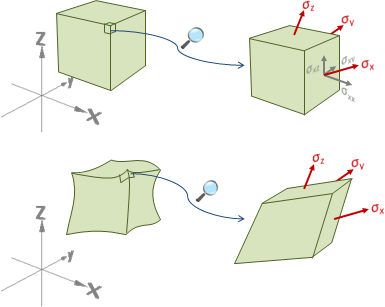
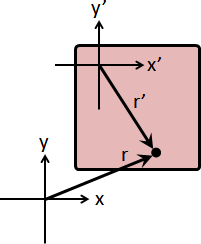
reference frame

參考系。更換座標系統。更換原點與座標軸。

甚至指定運動軌跡。原點與座標軸，隨著時間不斷變化。

中文翻譯不到位。直譯是參考框，含義是攝影機沿路跟拍。

參考系的主要用途是建立數學公式。

Euler's equation：旋轉運動，使用參考系。

Newton–Euler equation：平移運動、旋轉運動，使用參考系。

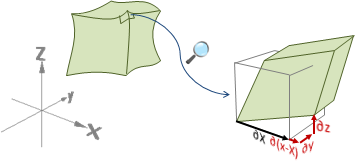
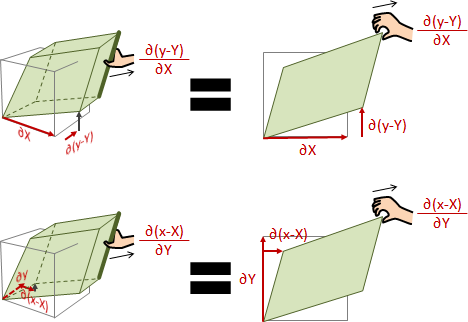
relative motion

相對運動。兩個質點的運動量差異。

文言文。剛體當中任意兩個質點A與B。B的運動量減去A的運動量，就是B相對於A的運動量。

白話文。參考系，原點定為A，座標軸定為標準座標軸。也就是說，剛體運動過程，各個時刻的畫面，各自將A平移至原點。然後再來觀察B的運動量。站在A，觀察B。剛體做平移運動，而B做相對平移運動，B相對平移速度是零。剛體做旋轉運動，而B做相對旋轉運動，B相對旋轉速度恰好等於剛體旋轉速度。

相對運動的主要用途是建立數學公式。推導過程源自這份講義。

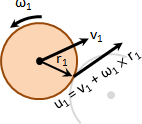
剛體質點速度。拆成兩項，平移速度與旋轉速度。

v = vₒ + ωₒ × rₒ

剛體質點加速度。拆成兩項，切線加速度與向心加速度（切線與法線）。

a = αₒ × rₒ + ωₒ × (ωₒ × rₒ)

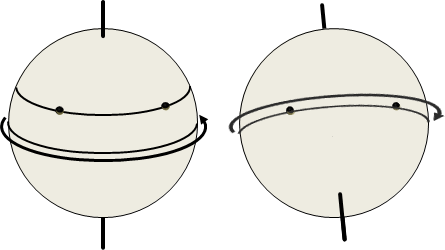
rotating reference frame

旋轉參考系。參考系做等速自旋運動。

旋轉參考系的主要用途是地球自轉。在地球觀察物體運動，需要旋轉參考系。推導過程源自這份講義。

質點速度。拆成兩項，旋轉參考系質點速度與相對角速度。

vɪ = vʀ + (ω̃ × r̃)

[]ɪ: inertial reference frame
[]ʀ: rotating reference frame

r = rₓeₓ + r₝e₝ + r₞e₞ = sum rᵢeᵢ
r̃ = r̃ₓẽₓ + r̃₝ẽ₝ + r̃₞ẽ₞ = sum r̃ᵢẽᵢ
r = õ + r̃

[d/dt r]ɪ = [d/dt õ]ɪ + [d/dt r̃]ɪ
          = [d/dt õ]ɪ + [sum (d/dt r̃ᵢ)ẽᵢ]ɪ + [sum r̃ᵢ(d/dt ẽᵢ)]ɪ
          = [d/dt õ]ɪ + [d/dt r̃]ʀ + [ω̃ × r̃]ɪ
^^^^^^^^^   ^^^^^^^^^   ^^^^^^^^^   ^^^^^^^^
    vɪ          0          vʀ        ω̃ × r̃

質點加速度。拆成三項，旋轉參考系質點加速度、地轉偏向加速度、離心加速度。

aɪ = aʀ + 2(ω̃ × vʀ) + ω̃ × (ω̃ × r̃)

[d/dt vɪ]ɪ = [d/dt d/dt õ]ɪ + [d/dt vʀ]ɪ + [d/dt (ω̃ × r̃)]ɪ
             ^^^^^^^^^^^^^^   ^^^^^^^^^^   ^^^^^^^^^^^^^^^
[d/dt d/dt õ]ɪ = 0
[d/dt vʀ]ɪ = [d/dt vʀ]ʀ + [ω̃ × vʀ]ɪ
[d/dt (ω̃ × r̃)]ɪ = [(d/dt ω̃) × r̃]ɪ + [ω̃ × (d/dt r̃)]ɪ
                = [α̃ × r̃]ɪ + [ω̃ × (vʀ + (ω̃ × r̃))]ɪ
                =    0     + [ω̃ × vʀ]ɪ + [ω̃ × (ω̃ × r̃)]ɪ

[d/dt vɪ]ɪ = [d/dt vʀ]ʀ + [2(ω̃ × vʀ)]ɪ + [ω̃ × (ω̃ × r̃)]ɪ
^^^^^^^^^^   ^^^^^^^^^^   ^^^^^^^^^^^^   ^^^^^^^^^^^^^^
    aɪ           aʀ        2(ω̃ × vʀ)      ω̃ × (ω̃ × r̃)
                          Coriolis acc.  centrifugal acc.

angular momentum ≠ rotational momentum

物理教科書竄改了旋轉動量（角動量）的定義。

物理教科書將角動量直接定義為L=r×p。線動量乘以「線動量延長線到參考點的距離」，並且推廣成向量。參考點可以是任意點，不必是旋轉中心。參考點只有一個，不能設置多個。

角動量不再是旋轉動量！除非將參考點設於旋轉中心，而且物體只有一個！成為歷史共業。

angular momentum conversation

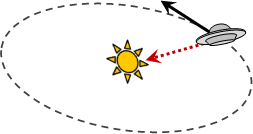
角動量守恆。指定任意一個參考點，每個質點的角動量，總和是定值。

注意到，這個定律並非在說「每個物體，各自計算旋轉動量，根據自身旋轉中心」，而是在說「所有物體使用同一個參考點計算角動量」。物理學家並未發現旋轉動量守恆，只發現角動量守恆。現實世界似乎也不存在旋轉動量守恆。

注意到，這個定律只適合用在單一質點平移、大量質點平移、單一物體旋轉，不適合用在大量物體旋轉。

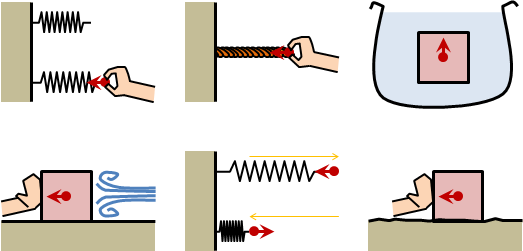
couple

力偶。每個質點，各自受力，總和恰為零。

∑ Fᵢ = 0

指定參考點位置，可以求得角動量變化快慢（力矩）。

M = ∑ (rᵢ × Fᵢ)

力偶的重要性質：各種參考點位置，角動量變化快慢（力矩）皆相同。稱作Varignon's theorem。

M̃ = ∑ r̃ᵢ × F̃ᵢ
  = ∑ r̃ᵢ × Fᵢ
  = ∑ (rᵢ - õ) × Fᵢ
  = ∑ (rᵢ × Fᵢ) - ∑ (õ × Fᵢ)
  = ∑ (rᵢ × Fᵢ) - (õ × ∑ Fᵢ)
  = ∑ (rᵢ × Fᵢ) -     0
  = M

換句話說，不必煩惱參考點位置。

物體不適合使用力偶。一個質點受力之後，其他質點是否因此受力、受到多少力，我們無從得知。也就無法確認力偶。

物體使用力偶，需要額外假設。假設施力不會傳遞到其他質點、假設無視旋轉慣量。例如物體沒有厚度。槓桿定律law of the lever也隱含著類似的假設。真實世界的細棍、薄板，大致符合這些假設，得以使用力偶。

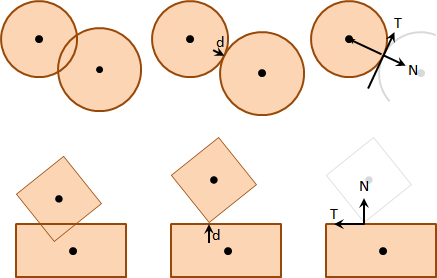
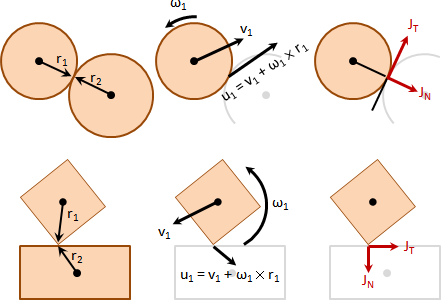
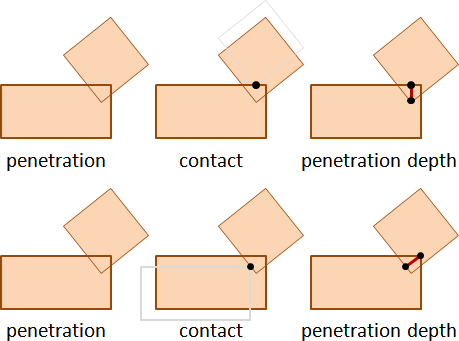
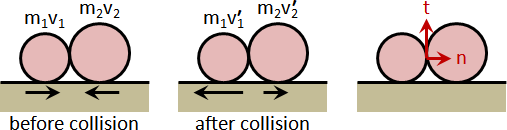
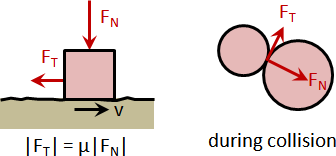
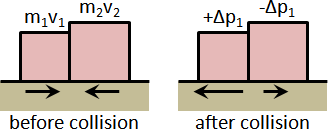
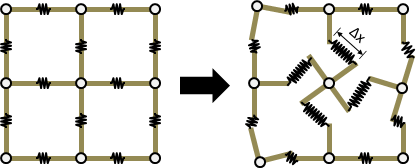
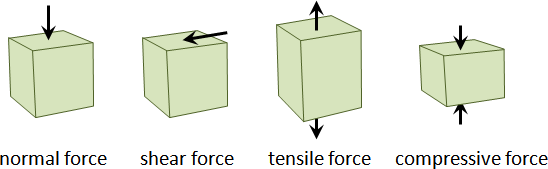
rigid body contact force

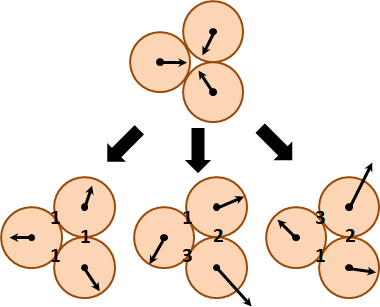
一、均勻施力於剛體的每個質點。

平移運動：根據數學的分配律，剛體平移動量化作質心平移動量，剛體平移速度化作質心平移速度。

旋轉運動：當旋轉中心是質心，力矩總和最小。根據最小作用量原理，旋轉中心是質心。依據是tennis racket theorem與parallel axis theorem，轉動慣量達到最小。

因此，剛體移動＋剛體轉動＝質心移動＋質心轉動。

甚至進一步使用參考系，將原點位置設為質心位置。

二、施力於剛體的一個質點。

平移動量與旋轉動量各占多少？如何求得旋轉中心？我不知道。

物理學家傾向採用另一套數學模型，請見柔體模擬章節。那套數學模型採用另一種世界觀，不存在所謂的剛體。

如果你堅持使用目前這套數學模型，那麼首先需要釐清剛體的各個質點如何互動。你必須自行腦補一些principle，進行二次創作，才能繼續談下去。

principle就好比是世界觀基本設定，精靈善弓、矮人善斧。principle是物理學家觀察真實世界而得到的經驗。principle可以想成是不太嚴謹的數學律。

以下介紹其中幾個principle，針對目前這套數學模型。

d'Alembert's principle

靜力平衡原理。

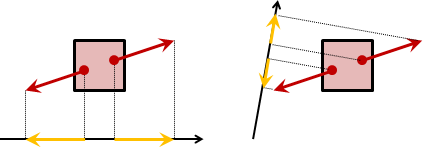
當物體動量不變，那麼任意位置的任意方向，合力為零。

物理學家根據此原理，設計出平移動量的定義。

principle of transmissibility

施力傳遞原理。

更改施力位置，沿著施力正反方向，功效皆相同：一、動量變化皆相同。二、角動量變化皆相同（直線到參考點的距離是定值。）

物理學家根據此原理，設計出平移動量、角動量的定義。

注意到，這個原理並非在說「旋轉中心皆相同」。旋轉中心通常皆不同，旋轉中心通常不是質心。

principle of least action

最小作用量原理。

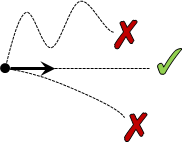
物質運動，總是選擇能量損失最少的軌跡。能省則省。

物質未受力，軌跡是直線。物質持續受力（例如重力），軌跡是拋物線。

物理學家根據此原理，設計出能量的定義。

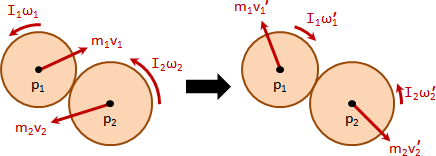
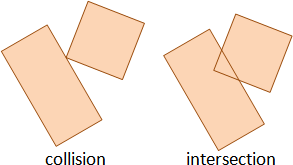
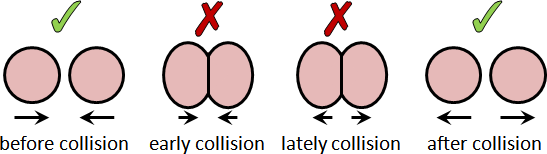
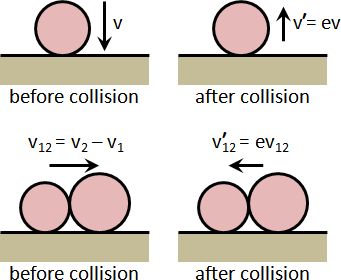
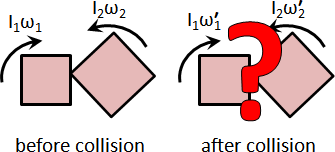
rigid body collision

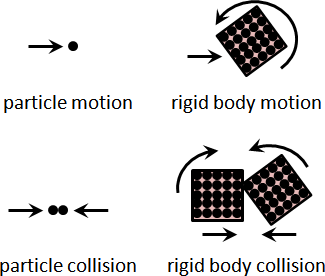
我翻閱了大量的力學書籍。我找到質點運動、剛體運動、質點碰撞，就是找不到剛體碰撞。有機會我再調查一下力學論文吧。

我搜尋了許多的網路論壇。我找到兩種解題策略：一、找到接觸位置，視作質點碰撞。反推旋轉中心。二、找到質心位置，視作質點碰撞。利用動量守恆、角動量守恆，解聯立方程式。

我認為這些解題策略都是二次創作。各有各的道理。

架構

rigid body collision (via particle collision)
├ momentum
├ friction / restitution
├ energy
└ impulse

collision

碰撞。兩個物體，從接觸到脫離，從擠壓變形到恢復原形。

不一定可以完全恢復原形。

物體運動過程劃分四個階段：

碰撞之前：有間隙。位置持續靠近，間隙持續變小。

碰撞前期：無間隙。位置持續靠近，物體持續擠壓變形。

碰撞後期：無間隙。位置持續遠離，物體持續恢復原形。

碰撞之後：有間隙。位置持續遠離，間隙持續變大。

計算學當中，只看碰撞前後，不看碰撞期間。不計碰撞時間、無視形狀變化，得以簡化演算法。

現實世界當中，堅硬的物體，碰撞時間非常短，變形幅度非常小，肉眼無法察覺。計算學的簡化方式，迎合現實，不無道理。

particle collision / rigid body collision

物理學當中，「質點碰撞」和「剛體碰撞」是不同的數學模型！中學教科書總是生搬硬套，拿質點碰撞去算剛體碰撞。大學教科書則是分開造冊，質點碰撞屬於靜力學與動力學，剛體碰撞屬於連體力學與接觸力學。

剛體碰撞產生的平移運動，碰巧能用質點碰撞來計算。剛體碰撞也引入了動量守恆，恰好相容，不會導致邏輯矛盾。

剛體碰撞產生的旋轉運動，無法利用質點碰撞來計算。一方面質點碰撞不存在旋轉運動，一方面剛體碰撞並未引入角動量守恆。大家還是可以強行計算，只不過那是未定義行為，不知道會發生什麼鳥事。

接下來介紹如何用質點碰撞去算剛體碰撞。

translational momentum

碰撞過程，動量總和不變。動量守恆。

m₁v₁ + m₂v₂ = m₁v₁' + m₂v₂'

碰撞過程，法線方向相對速度變號。完全彈性。

(v₂' - v₁') ∙ n = (v₂ - v₁) ∙ n

碰撞過程，切線方向速度不受影響。完全光滑。

⎰ v₁ ∙ t = v₁' ∙ t
⎱ v₂ ∙ t = v₂' ∙ t

已知原速度、質量，求得新速度。

⎧ m₁v₁ + m₂v₂ = m₁v₁' + m₂v₂'
⎨ (v₂' - v₁') ∙ n = (v₂ - v₁) ∙ n
⎪ v₁ ∙ t = v₁' ∙ t
⎩ v₂ ∙ t = v₂' ∙ t

現實世界並非完全彈性、完全光滑，必須考慮恢復、摩擦。

restitution

牛頓以新舊相對速度的比值，衡量恢復程度，稱作恢復係數。

e = |v₁₂'| / |v₁₂|     都是純量

換句話說，牛頓以舊相對速度，求得新相對速度。藉由乘上一個恢復係數。

v₂' - v₁' = -e (v₂ - v₁)     都是純量

0表示毫無恢復（完全非彈性碰撞）。相對速度變成零，兩物黏在一起。

1表示完全恢復（彈性碰撞）。

0 ≤ e ≤ 1
e = 0 保持接觸，黏在一起，動能散失
e = 1 彈性碰撞，動能無損

translational momentum: restitution

碰撞過程，動量總和不變。稱作動量守恆。

m₁v₁ + m₂v₂ = m₁v₁' + m₂v₂'

碰撞過程，相對速度改變。根據恢復係數。

（間接決定了動量差異多寡。）

v₂' - v₁' = -e (v₂ - v₁)

已知原速度、質量、恢復係數，求得新速度。

（已知原動量、動量總和不變、動量差異多寡，求得新動量。）

⎰ m₁v₁ + m₂v₂ = m₁v₁' + m₂v₂'
⎱ v₂' - v₁' = -e (v₂ - v₁)

二維。

⎧ m₁v₁ + m₂v₂ = m₁v₁' + m₂v₂'
⎨ (v₂' - v₁') ∙ n = -e (v₂ - v₁) ∙ n
⎪ v₁ ∙ t = v₁' ∙ t
⎩ v₂ ∙ t = v₂' ∙ t

牛頓恢復與牛頓動量是兩套理論，但是可以併用。

恢復係數源自物體落地反彈高度。

friction

庫侖觀察法線方向、切線方向的動量變化程度（力），以兩者的比值，衡量摩擦程度，稱作摩擦係數。

μ = |Fᴛ| / |Fɴ|

換句話說，庫侖以法線方向的動量變化，求得切線方向的動量變化。藉由乘上一個摩擦係數。

|Fᴛ| ≤ μ |Fɴ|     都是純量

0表示毫無摩擦（完全光滑）。切線不受法線影響。

可以大於1。

μ ≥ 0
μ = 0 毫無摩擦、完全光滑

translational momentum: friction

碰撞過程，動量總和不變。稱作動量守恆。

m₁v₁ + m₂v₂ = m₁v₁' + m₂v₂'

碰撞過程，法線方向相對速度改變。根據恢復係數。

(v₂' - v₁') ∙ n = -e (v₂ - v₁) ∙ n

碰撞過程，切線方向動量轉移受限。根據摩擦係數。

(m₁v₁' - m₁v₁) ∙ t = -(m₂v₂' - m₂v₂) ∙ t = μ |(m₂v₂ - m₁v₁) ∙ n|

已知原速度、質量、恢復係數、摩擦係數，求得新速度。

⎧ m₁v₁ + m₂v₂ = m₁v₁' + m₂v₂'
⎨ (v₂' - v₁') ∙ n = -e (v₂ - v₁) ∙ n
⎩ (m₁v₁' - m₁v₁) ∙ t = -(m₂v₂' - m₂v₂) ∙ t = μ |(m₂v₂ - m₁v₁) ∙ n|

庫侖摩擦與牛頓動量是兩套理論，併用導致邏輯矛盾。例如Painlevé paradox，未定義行為導致怪事發生。

附帶摩擦的碰撞，必須使用更複雜的理論！此處介紹的方式，只是計算學家的一廂情願。做個動畫，圖個快樂，無傷大雅。

translational energy

碰撞過程，動量總和不變。動量守恆。

m₁v₁ + m₂v₂ = m₁v₁' + m₂v₂'

完全恢復的情況下，能量總和也不變。能量守恆。

⎰ m₁v₁ + m₂v₂ = m₁v₁' + m₂v₂'
⎱ ½m₁v₁² + ½m₂v₂² = ½m₁v₁'² + ½m₂v₂'²

沒有完全恢復的情況下，視作一部分的動能轉換成內能（物體結構本身蘊含的能量）。

⎰ m₁v₁ + m₂v₂ = m₁v₁' + m₂v₂'
⎱ ½m₁v₁² + ½m₂v₂² = ½m₁v₁'² + ½m₂v₂'² + K

楊能量與牛頓動量是兩套理論，但是可以併用。

詳情我沒有研究。

rotational momentum

質點碰撞不存在旋轉運動。用質點碰撞去算剛體碰撞，要是算出旋轉動量，只可能是二次創作。

impulse

衝量。一個物體，動量先後差異。

p = mv                   momentum
Δp = p' - p = mv' - mv   impulse

兩個物體碰撞，動量相互轉移，衝量相等但是異號。

p₁ = m₁v₁                     momentum
Δp₁ = p₁' - p₁ = mv₁' - mv₁   impulse

p₂ = m₂v₂                     momentum
Δp₂ = p₂' - p₂ = mv₂' - mv₂   impulse

Δp₁ = -Δp₂                    momentum transfer

想要求得新速度，亦可利用衝量。

translational impulse

兩個物體各有平移動量：

p₁ = m₁v₁
p₂ = m₂v₂

兩個物體發生碰撞，平移動量守恆：

p₁ + p₂ = p₁' + p₂'

三式聯立，可以推導平移衝量公式：

┌──────────┐   ┌───────────┐┌─────────────────────────┐
│ p₁ - p₁' │   │     1     ││                         │
│          │   │ ————————— ││                         │
│    or    │ = │  1    1   ││ (v₂' - v₁') - (v₂ - v₁) │
│          │   │  —— + ——  ││                         │
│ p₂' - p₂ │   │  m₁   m₂  ││                         │
└──────────┘   └───────────┘└─────────────────────────┘
  impulse      reduced mass change in relative velocity
    Δp₂             m₁₂*                Δv₁₂

上述公式可用物理術語描述：

「衝量pulse」。第二物的動量先後差異。

「約化質量reduced mass」。兩物質量調和平均數的一半。

「相對速度relative velocity的先後差異」。兩物速度差異的先後差異。

考慮恢復、摩擦，平移衝量公式更加複雜，此處省略。

rotational impulse

然而旋轉衝量公式存在疑慮！按照原本思路，重跑一遍流程：

兩個物體各有旋轉動量：

L₁ = I₁ω₁
L₂ = I₂ω₂

兩個物體發生碰撞，旋轉動量守恆：

L₁ + L₂ = L₁' + L₂'   ✘

三式聯立，可以推導旋轉衝量公式：

┌──────────┐   ┌───────────┐┌─────────────────────────┐
│ L₁ - L₁' │   │     1     ││                         │
│          │   │ ————————— ││                         │
│    or    │ = │  1    1   ││ (ω₂' - ω₁') - (ω₂ - ω₁) │   ✘
│          │   │  —— + ——  ││                         │
│ L₂' - L₂ │   │  I₁   I₂  ││                         │
└──────────┘   └───────────┘└─────────────────────────┘
angular impulse      ?       change in relative angular velocity
     ΔL₂            I₁₂*                Δω₁₂

但是物理學家並未發現旋轉動量守恆。物理學應該沒有這樣的定律。現實世界似乎也沒有這樣的事實。

物理學家只有發現角動量守恆。所謂的角動量，必須指定一個參考點。將參考點同時指定為兩物的旋轉中心，屬於未定義行為。

collision

碰撞。兩個物體運動，相互接觸，動量轉移。

slipping / rolling

兩個物體運動，隨時保持接觸。

滑動：平移運動。滾動：旋轉運動。

spin / precession

陀螺同時做兩種運動。

自旋：軸心轉動。進動：軸心移動（圓周運動）。

gyroscopic effect

當物體形如陀螺，物體會側滾。源自進動。

Dzhanibekov effect

當物體形如球拍，物體每隔一段時間會翻面。源自進動。

fluid simulation

流體模擬。物質不具備特定造型，物質四處運動。

對應到連體力學之流體力學。

資源

http://bugman123.com/FluidMotion/
https://developer.nvidia.com/
http://pof.tnw.utwente.nl/research
http://panoramx.ift.uni.wroc.pl/~maq/eng/index.php

演算法一覽

流體模擬有兩種策略：

粒：紀錄每一個水滴的位置、速度、加速度（力）。

格：紀錄每一個位置的水滴總數量、總速度、總加速度（力）。

物理學術語分別是拉格朗日描述、歐拉描述。

數學術語分別是粒子法、有限體積法。

粒格衍生許多演算法：粒連續SPH、粒離散SEC、粒方程PDB、粒化格PIC、格八方LBM、格中粒MAC、格中格MG。

近期的演算法：PCISPH、PIC/FLIP、Affine PIC、……。

這篇文章針對各種演算法進行歷史回顧。

粒

模擬流程。源自LiquidFun的說明文件、這篇文章。

function update() { force(); // compressibility + viscosity bound(); move(); }

粒子。建立100個粒子，隨機散布。

粒子擁有位置、速度、加速度（力）。

function Particle() { return { // m: 1, x: Math.random() * canvas.width, y: Math.random() * canvas.height, vx: 0, vy: 0, ax: 0, ay: 0 } } const N = 100; var particles = []; function init() { particles = []; for (let i=0; i<N; i++) particles.push(Particle()); }

運動。考慮兩種力。

一、壓縮力：法線方向。設定為彈簧力。

二、黏滯力：切線方向。設定為阻尼力。

壓縮力。粒子互相推擠，導致外散。

粒子侵入深度ｘ彈性係數＝壓縮力。

距離改成距離比值，並且升高次方。低次方令粒子塌陷，高次方令粒子鞏固（彈性係數也要隨之增加）。水不可壓縮，理論上次方值非常大，實務上取平方就足夠耐看了。

function force() { for (let p1 of particles) { p1.ax = p1.ay = 0; for (let p2 of particles) addforce(p1, p2); } } function addforce(p1, p2) { // compressibility var dx = p2.x - p1.x; var dy = p2.y - p1.y; var d = Math.sqrt(dx*dx + dy*dy); if (d < 0.001) d = 0.001; // 避免除以0 const diameter = 12; // 彈簧長度 if (d >= diameter) return; // 粒子未接觸 const compressibility = 1; // 彈性係數 var s = (diameter - d) / diameter; s = s * s; // 距離比值二次方 p1.ax += compressibility * s * -dx/d; // 彈力 p1.ay += compressibility * s * -dy/d; // viscosity ...... }

黏滯力。粒子互相摩擦，導致連動。

相對速度的切線分量ｘ阻尼係數＝黏滯力。

切線分量改成法線分量，簡化計算。副作用是多了個緩速，無傷大雅。法線分量＝相對速度－切線分量。相對速度乘上係數之後，效果是緩速。

function addforce(p1, p2) { // compressibility ...... // viscosity var dvx = p2.vx - p1.vx; var dvy = p2.vy - p1.vy; var dot = dx*dvx + dy*dvy; const viscosity = 0.1; // 阻尼係數 p1.ax += viscosity * dot/d * dx/d; p1.ay += viscosity * dot/d * dy/d; }

鄰居。兩層迴圈窮舉所有點對，O(N²)，太慢了。採用資料結構uniform grid，檢查周圍九宮格，O(N+K)，快多了。

const diameter = 12; // 彈簧長度 const grid = Math.ceil(canvas.height / diameter); var grids = []; function pushgrid(p) { var x = p.x / diameter | 0; var y = p.y / diameter | 0; var k = x * grid + y; grids[k] = grids[k] || []; grids[k].push(p); } function neighbors(p) { var array = new Array(); var x = p.x / diameter | 0; var y = p.y / diameter | 0; var ix = [-1,-1,-1,0,0,0,1,1,1]; var iy = [-1,0,1,-1,0,1,-1,0,1]; for (let i=0; i<9; ++i) { var k = (x+ix[i]) * grid + (y+iy[i]); if (grids[k]) array = array.concat(grids[k]); } return array; } function force() { grids = []; for (let p1 of particles) pushgrid(p1); for (let p1 of particles) { p1.ax = p1.ay = 0; for (let p2 of neighbors(p1)) addforce(p1, p2); } }

移動。加速度ｘ時間＝速度。速度ｘ時間＝移動距離。

步幅。移動不得穿越粒子，否則粒子可能高速噴射。保守策略是移動距離小於相間距離。Δt足夠小，力與速度足夠小。

function move() { const dt = 1; for (let p of particles) { p.vx += p.ax * dt; p.vy += p.ay * dt; p.x += p.vx * dt; p.y += p.vy * dt; } }

牆壁。粒子撞牆有兩種解法：

一、粒子反彈：位置鏡射回來、速度顛倒方向。

二、牆如粒子：牆給予粒子壓縮力。

function bound() { for (let p of particles) { const compressibility = 1; // 彈性係數 var r = diameter / 2; var x1 = r, x2 = canvas.width - r; var y1 = r, y2 = canvas.height - r; if (p.x < x1) p.ax += (x1 - p.x) * compressibility; else if (p.x > x2) p.ax -= (p.x - x2) * compressibility; if (p.y < y1) p.ay += (y1 - p.y) * compressibility; else if (p.y > y2) p.ay -= (p.y - y2) * compressibility; } }

繪圖。粒子畫成圓形、正方形、三角形，隨你開心。

function draw() { const size = 1; ctx.clearRect(0, 0, canvas.width, canvas.height); ctx.fillStyle = 'blue'; for (let p of particles) ctx.fillRect(p.x - size/2, p.y - size/2, size, size); }

粒：空氣與水

重力。粒子添加一道力。理論上是9.8，實務上自訂。

function force() { ...... const gravity = 0.2; for (let p of particles) p.ay += gravity; }

繪圖。粒子不要畫成圓球，而是畫成blobby surface。想要更擬真，則需要3D graphics的知識。

const size = 12; // 圓形半徑 // 漸層透明圓形 var node2 = (function(){ var canvas = document.createElement("canvas"); canvas.width = canvas.height = size * 2; var ctx = canvas.getContext('2d'); var gradient = ctx.createRadialGradient(size, size, 1, size, size, size); grad.addColorStop(0, 'hsla(240, 80%, 60%, 1)'); grad.addColorStop(1, 'hsla(240, 80%, 60%, 0)'); ctx.fillStyle = gradient; ctx.beginPath(); ctx.arc(size, size, size, 0, Math.PI * 2, true); ctx.fill(); return canvas; })(); function draw2() { // 漸層透明圓形，疊加於畫布。 ctx.clearRect(0, 0, canvas.width, canvas.height); for (let p of particles) ctx.drawImage(node2, p.x-size, p.y-size); // 取RGBA的透明度A，作為blobby surface臨界值。 var imageData = ctx.getImageData(0, 0, canvas.width, canvas.height); var pix = imageData.data; var threshold = 180; for (let i = 0; i < pix.length; i += 4) pix[i + 3] = (pix[i + 3] < threshold) ? 0 : 255; ctx.putImageData(imageData, 0, 0); }

格

模擬流程。源自這套教材、這本書籍。

function update() { boundary(u, v); // 計算邊界速度 interior(u, v); // 計算內部速度 project(u, v); // 校正速度，使得處處出入相等 }

格子。建立40×40個格子。

只紀錄速度。不紀錄數量：假設粒子密度均勻不變，假設數量是常數。不紀錄加速度：加速度乘上時間，直接添加到速度。

配置。兩種方式。

colocated grid：速度在格中央。
staggered grid：X速度在格左右，Y速度在格上下。

此處採用staggered grid。兩點優勢：一、水衝撞牆，會往兩側散開，不會只往其中一側流動。二、計算散度，會更加精確，不會省略中央速度。

上下添加一排X速度，以便內插上下牆壁附近的X速度。左右添加一排Y速度，以便內插左右牆壁附近的Y速度。

var N = 40; var u = new Float32Array2D(N+1, N+2); var u0 = new Float32Array2D(N+1, N+2); // temp var v = new Float32Array2D(N+2, N+1); var v0 = new Float32Array2D(N+2, N+1); // temp function Float32Array2D(n, m) { var a = new Array(n); for (let i=0; i<n; ++i) a[i] = new Float32Array(m).fill(0); return a; }

牆壁。四種方式。數學術語是邊界條件。

  no-slip condition：牆壁沾黏，切線速度是特定值。
free-slip condition：牆壁光滑，切線速度等於鄰水速度。
   inflow condition：牆壁插管，法線速度是特定值。
  outflow condition：牆壁虛設，法線速度等於鄰水速度。

此處採用no-slip。水被牆壁帶動，牆壁切線速度是自訂數值；水不可穿牆，牆壁法線速度是零。

牆內速度、牆外速度，內插得到牆壁速度。以此反推牆外速度。

function boundary(u, v) { var un=-1, us=+1, ve=-1, vw=+1; for (let i=1; i<=N; i++) u[i][0] = 2*un-u[i][1]; for (let i=1; i<=N; i++) u[i][N+1] = 2*us-u[i][N]; for (let j=1; j<=N; j++) v[0][j] = 2*vw-v[1][j]; for (let j=1; j<=N; j++) v[N+1][j] = 2*ve-v[N][j]; }

運動。考慮兩種現象。

diffuse：擴散。格中粒子均勻四散，其速度也隨之均勻四散。

         ∂          ∂       ∂         ∂          ∂       ∂      
         —— u = ν ( ——— u + ——— u )   —— v = ν ( ——— v + ——— v )
         ∂t         ∂x²     ∂y²    ,  ∂t         ∂x²     ∂y²
               ^^^                          ^^^
         這兩個是擴散速率。
         小寫希臘字母ν，唸作/njuː/，寫作nu。不是小寫英文字母v。

   flow：流動。格中粒子依照自身速度集體移動，其速度也隨之集體移動。

         ∂          ∂       ∂         ∂          ∂       ∂      
         —— u = - ( —— uu + —— vu )   —— v = - ( —— uv + —— vv )
         ∂t         ∂x      ∂y     ,  ∂t         ∂x      ∂y     

數學術語是hydrodynamic equation與Euler method。

const h = 1/N; // Δx = Δy = h const dt = 0.001; // Δt const nu = 0.1; // kinematic viscosity ν function interior(u, v) { // x-velocity for (let i=1; i<=N-1; i++) for (let j=1; j<=N; j++) { // diffuse var laplace = u[i+1][j] + u[i-1][j] + u[i][j+1] + u[i][j-1] - 4 * u[i][j]; // flow var uu_x = Math.pow(u[i+1][j] + u[i][j], 2) - Math.pow(u[i][j] + u[i-1][j], 2); var uv_y = (u[i][j+1] + u[i][j]) * (v[i+1][j] + v[i][j]) - (u[i][j] + u[i][j-1]) * (v[i+1][j-1] + v[i][j-1]); // 擴散暨流動，求得加速度。 var a = nu*laplace/h/h - (uu_x+uv_y)/4/h; u0[i][j] = u[i][j] + a * dt; } // [u, u0] = [u0, u]; // javascript pass by value // swap after calling function // y-velocity for (let i=1; i<=N; i++) for (let j=1; j<=N-1; j++) { // diffuse var laplace = v[i+1][j] + v[i-1][j] + v[i][j+1] + v[i][j-1] - 4 * v[i][j]; // flow var vv_y = Math.pow(v[i][j+1] + v[i][j], 2) - Math.pow(v[i][j] + v[i][j-1], 2); var uv_x = (u[i][j+1] + u[i][j]) * (v[i+1][j] + v[i][j]) - (u[i-1][j+1] + u[i-1][j]) * (v[i][j] + v[i-1][j]); // 擴散暨流動，求得加速度。 var a = nu*laplace/h/h - (uv_x+vv_y)/4/h; v0[i][j] = v[i][j] + a * dt; } // [v, v0] = [v0, v]; // javascript pass by value // swap after calling function }

步幅。移動不得穿越格子，否則速度可能高速逸散。保守策略是移動距離小於格子寬度。

數學術語是穩定條件CFL condition。格子邊長Δx越窄，時間差距Δt越小。格子越細膩，步幅越短小，動畫越緩慢。

const h = 1/N; // 格子邊長。 const dt = 0.001; // 時間差距。影響步幅。不得穿越格子。 const nu = 0.1; // 擴散係數。影響擴散速度。不得穿越格子。

不可壓縮。格中粒子速度，出入總量相等，流動順暢。

incompressibility：不可壓縮。

                   ∂      ∂       
                   —— u + —— v = 0
                   ∂x     ∂y      

按理來說，擴散、流動、不可壓縮必須同時聯立，一口氣求得新速度。不幸的是，大家尚未發現漂亮的解法。別無選擇，只好逐個計算。首先擴散與流動，接著校正速度場，使之不可壓縮。

數學術語是散旋諧分解。依序計算散度、散勢（壓力）、散場。速度場減去散場，使得速度場的散度變成零，成為無散場。

數學術語是投影。給定速度場，找到平方誤差最小的無散場。

var p = new Float32Array2D(N+2, N+2); var div = new Float32Array2D(N+2, N+2); function project(u, v) { // get divergence (without dividing h) for (let i=1; i<=N; ++i) for (let j=1; j<=N; ++j) div[i][j] = u[i][j] - u[i-1][j] + v[i][j] - v[i][j-1]; // solve for pressure (without dividing h) solve(p, div); // remove divergence field for (let i=1; i<=N-1; ++i) for (let j=1; j<=N; ++j) u[i][j] -= (dt/h)*(p[i+1][j]-p[i][j]); for (let i=1; i<=N; ++i) for (let j=1; j<=N-1; ++j) v[i][j] -= (dt/h)*(p[i][j+1]-p[i][j]); }

鄰居。投影時，牆壁不計入。牆壁壓力設為零，作為無效的分子；事先算好鄰居有幾格，作為分母。

var c = new Float32Array2D(N+2, N+2); neighbor(); function neighbor() { // 不靠牆處 for (let i=2; i<=N-1; i++) for (let j=2; j<=N-1; j++) c[i][j] = 4; // 靠牆邊 for (let i=2; i<=N-1; i++) c[1][i] = c[N][i] = c[i][1] = c[i][N] = 3; // 靠牆角 c[1][1] = c[1][N] = c[N][1] = c[N][N] = 2; }

求解。一次方程組求解，兩種演算法。

SOR：稀疏矩陣，適合鬆弛法。容易實作，但是收斂速度慢。
PCG：半正定矩陣，適合共軛梯度法。請見這篇講義。

數學術語是discrete Poisson equation。

// successive over-relaxation const beta = 1.2; // magic number const iteration = 100; function solve(p, div) { for (let k=0; k<iteration; ++k) for (let i=1; i<=N; ++i) for (let j=1; j<=N; ++j) { var sum = p[i+1][j] + p[i-1][j] + p[i][j+1] + p[i][j-1]; p[i][j] = beta*(sum-(h/dt)*div[i][j])/c[i][j] + (1-beta)*p[i][j]; } } // preconditioned conjugate gradient var M = new Float32Array2D(N+2, N+2); var r = new Float32Array2D(N+2, N+2); var s = new Float32Array2D(N+2, N+2); var z = new Float32Array2D(N+2, N+2); var q = new Float32Array2D(N+2, N+2); function solve(x, b) { fill(x, 0); // x = 0 if (dot(b, b) < 1e-6) return; // b == 0 copy(r, b); // r = b negate(r); // r = -b buildPreconditioner(M); applyPreconditioner(M, r, z); // z = f(r) var a = dot(z, r); // a = z . r for (let k=0; k<N*N; k++) { copy(s, z); // s = z compute_Ax(s, z); // z = A(s) var alpha = a / dot(z, s); add(x, s, +alpha); // x += alpha * s add(r, z, -alpha); // r -= alpha * z var e = dot(r, r); // e = r . r if (e/(N*N) < 1e-6) break; applyPreconditioner(M, r, z); // z = f(r) var anew = dot(z, r); // anew = z . r var beta = anew / a; add(z, s, +beta); // z += beta * s a = anew; } } // modified incomplete Cholesky preconditioner const tau = 0.97; // magic number function buildPreconditioner(M) { for (let i=1; i<=N; ++i) for (let j=1; j<=N; ++j) { var ai = M[i-1][j] * M[i-1][j]; var aj = M[i][j-1] * M[i][j-1]; var e = c[i][j] - (1 - tau) * (ai + aj); M[i][j] = 1 / Math.sqrt(e + 1e-6); } } // forward substitution and backward substitution function applyPreconditioner(M, r, z) { // Lq = r for (let i=1; i<=N; ++i) for (let j=1; j<=N; ++j) { var ai = M[i-1][j] * q[i-1][j]; var aj = M[i][j-1] * q[i][j-1]; q[i][j] = (r[i][j] + ai + aj) * M[i][j]; } // Lᵀz = q for (let i=N; i>=1; --i) for (let j=N; j>=1; --j) { var ai = M[i][j] * z[i+1][j]; var aj = M[i][j] * z[i][j+1]; z[i][j] = (q[i][j] + ai + aj) * M[i][j]; } } // y = Ax function compute_Ax(x, y) { for (let i=1; i<=N; ++i) for (let j=1; j<=N; ++j) { var sum = x[i+1][j] + x[i-1][j] + x[i][j+1] + x[i][j-1]; y[i][j] = (c[i][j] * x[i][j] - sum) * (dt/h); } } // x = k function fill(x, k) { for (let i=1; i<=N; ++i) for (let j=1; j<=N; ++j) x[i][j] = k; } // x = y function copy(x, y) { for (let i=1; i<=N; ++i) for (let j=1; j<=N; ++j) x[i][j] = y[i][j]; } // x += k y function add(x, y, k) { for (let i=1; i<=N; ++i) for (let j=1; j<=N; ++j) x[i][j] += k * y[i][j]; } // z = x . y function dot(x, y) { var z = 0; for (let i=1; i<=N; ++i) for (let j=1; j<=N; ++j) z += x[i][j] * y[i][j]; return z; } // x = -x function negate(x) { for (let i=1; i<=N; ++i) for (let j=1; j<=N; ++j) x[i][j] = -x[i][j]; }

繪圖。速度場通常畫成軌跡圖、箭矢圖。亦得入境隨俗：

粒：散布大量粒子，沿著速度場跑。
格：建立粒子數量場（粒子濃度場），沿著速度場跑。

速度場繪圖方式：軌跡圖

function draw_velocity_field(u, v) { ctx.clearRect(0, 0, canvas.width, canvas.height); for (let i=1; i<=N; ++i) for (let j=1; j<=N; ++j) { var c = 0; // 軌跡起點：格中央 var x = i - 0.5; var y = j - 0.5; ctx.beginPath(); ctx.moveTo(x * width, y * width); // 軌跡路線：往回走五步 for (let k=0; k<5; ++k) { // 速度：一次內插取得更精確的速度。 // 速度位於格線，加0.5微調位置。 var cu = interpolate(u, x, y + 0.5); var cv = interpolate(v, x + 0.5, y); // 軌跡亮度：速度越快、軌跡越亮 var l = Math.sqrt(cu * cu + cv * cv); if (k == 0) c = (l * 255) | 0; // 軌跡路線：往回走一小步 if (l != 0) {cu /= l; cv /= l;} x -= cu; y -= cv; // 繪圖 ctx.lineTo(x * width, y * width); // 出界 if (!(x >= 0 && x < N && y >= 0 && y < N)) break; } ctx.lineWidth = 1; ctx.strokeStyle = 'rgba(' + c + ',' + c + ',' + c + ', 0.5)'; ctx.stroke(); } }

速度場繪圖方式：箭矢圖

function draw_velocity_field(u, v) { ctx.clearRect(0, 0, canvas.width, canvas.height); for (let i=1; i<=N; ++i) for (let j=1; j<=N; ++j) { // 箭矢尖銳程度 const slope = Math.PI / 18; // 箭矢長度 const length = 8; // 格中央速度 var cu = (u[i-1][j] + u[i][j]) / 2; var cv = (v[i][j-1] + v[i][j]) / 2; // 箭矢方向 var angle = Math.atan2(cv, cu); // 箭矢亮度：速度越高、箭矢越亮 var l = Math.sqrt(cu * cu + cv * cv); var c = (l * 255) | 0; if (l != 0) {cu /= l; cv /= l;} // 繪圖 ctx.save(); ctx.translate((i-0.5)*width, (j-0.5)*width); ctx.translate(cu, cv); ctx.beginPath(); ctx.moveTo(0, 0); ctx.lineTo(-length * Math.cos(angle-slope), -length * Math.sin(angle-slope)); ctx.lineTo(-length * Math.cos(angle+slope), -length * Math.sin(angle+slope)); ctx.closePath(); ctx.fillStyle = 'rgb(' + c + ',' + c + ',' + c + ')'; ctx.fill(); ctx.restore(); } }

速度場繪圖方式：粒

粒子。隨機散布大量粒子。

// 大量粒子 const P = 500; var particles = []; init_particles(); function init_particles() { for (let i=0; i<P; i++) { particles.push({ x: Math.random() * N, y: Math.random() * N, }); } }

繪圖。粒子畫成什麼形狀都行。

const width = (canvas.width / N) | 0; const size = 5; function draw_particles() { ctx.clearRect(0, 0, canvas.width, canvas.height); ctx.fillStyle = 'blue'; for (let p of particles) ctx.fillRect(p.x*width - size/2, p.y*width - size/2, size, size); }

流動。粒子沿著速度場跑。總共需要考慮：內插、步幅、步法、牆壁。

內插。取得更精確的速度。速度位於格線，加0.5微調位置。

步幅。採用更大的步幅，以便製作即時動畫。

步法。三種步法。以邪門歪道撥正軌跡。大家習慣採用one-step method，簡單走一步。數學術語是積分方法。

one-step method
1. 抓本地速度，走一步。

predictor–corrector method
1. 抓本地速度，走一步，到終點。
2. 抓本地與終點的平均速度，從頭重新走一步。

midpoint method
1. 抓本地速度，走半步，到中點。
2. 抓中點速度，從頭重新走一步。

牆壁。Δt畢竟不是無限微小，靠牆的水容易一步穿牆。穿牆粒子，放回牆內。

const speed = 1000; // 作弊增長步幅，以便讓動畫順暢。 function flow_particles(u, v) { for (let p of particles) { // 一次內插，取得更精確的速度。 // 速度位於格線，加0.5微調位置。 var pu = interpolate(u, p.x, p.y + 0.5); var pv = interpolate(v, p.x + 0.5, p.y); // 粒子沿著速度場跑。 p.x += pu * dt * speed; p.y += pv * dt * speed; // 穿牆粒子，放回牆內。 if (!(p.x >= 0 && p.x < N && p.y >= 0 && p.y < N)) { p.x = Math.random() * N; p.y = Math.random() * N; } } } function interpolate(a, x, y) { // bilinear interpolation var x0 = x | 0; var x1 = x0 + 1; var y0 = y | 0; var y1 = y0 + 1; var s1 = x - x0; var s0 = 1 - s1; var t1 = y - y0; var t0 = 1 - t1; return s0 * (t0 * a[x0][y0] + t1 * a[x0][y1]) + s1 * (t0 * a[x1][y0] + t1 * a[x1][y1]); }

速度場繪圖方式：格

格子。建立粒子數量場。

// 粒子數量場（粒子濃度場） var d = new Float32Array2D(N+2, N+2); var d0 = new Float32Array2D(N+2, N+2); // temp

繪圖。每一格根據粒子數量（粒子濃度），決定顏色深淺。

function draw_grids() { ctx.clearRect(0, 0, canvas.width, canvas.height); for (let i=1; i<=N; ++i) { for (let j=1; j<=N; ++j) { ctx.fillStyle = 'rgba(0,128,255,' + d[i][j] + ')'; ctx.fillRect((i-1) * width, (j-1) * width, width, width); } } }

流動。粒子數量沿著速度場跑。總共需要考慮：內插、步幅、步向、步法、牆壁、內插。

內插。取得更精確的速度。速度位於格線，加0.5微調位置。

步幅。採用更大的步幅，以便製作即時動畫。

步向。兩種方向。

forward
前進，往後補值。
優點是動量守恆。
缺點是空格與疊格。解法是縮小步幅、減少Δt。

backward
倒退，往前取值。
優點是流向精確。
缺點是零速度處無法流入、零速度處無限流出。解法是強制擴散。

步法。大家習慣採用backward步向、one-step method步法，兩者合稱semi-Lagrangian method。

牆壁。Δt畢竟不是無限微小，靠牆的水容易一步穿牆。一旦穿牆，立即挪回牆內。

內插。更精確的粒子數量。副作用是擴散。兩種方式。

前進與分配：根據面積大小分攤。
倒退與內插：一次內插、或者Catmull–Rom interpolation。
　　　　　　牆壁事先設定粒子數量，方便內插。

// forward function flow_grids(u, v, d) { for (let i=1; i<=N; i++) for (let j=1; j<=N; j++) d0[i][j] = 0; for (let i=1; i<=N; i++) { for (let j=1; j<=N; j++) { // 格子中央的速度 var cu = (u[i-1][j] + u[i][j]) / 2; var cv = (v[i][j-1] + v[i][j]) / 2; // 目的地 var x = (i + cu * dt * speed) | 0; var y = (j + cv * dt * speed) | 0; // 目的地必須在牆內 if (x < 1) x = 1; if (x > N) x = N; if (y < 1) y = 1; if (y > N) y = N; // 往後補值 distribute(d0, x, y, d[i][j]); } } // [d, d0] = [d0, d]; // javascript pass by value // swap after calling function } function distribute(a, x, y, v) { var x0 = x | 0; var x1 = x0 + 1; var y0 = y | 0; var y1 = y0 + 1; var s1 = x - x0; var s0 = 1 - s1; var t1 = y - y0; var t0 = 1 - t1; a[x0][y0] += s0 * t0 * v; a[x0][y1] += s0 * t1 * v; a[x1][y0] += s1 * t0 * v; a[x1][y1] += s1 * t1 * v; } // backward function boundary_grids(d) { // 牆壁事先設定粒子濃度：鄰水的粒子濃度 for (let i=1; i<=N; i++) d[i][0] = d[i][1]; for (let i=1; i<=N; i++) d[i][N+1] = d[i][N]; for (let j=1; j<=N; j++) d[0][j] = d[1][j]; for (let j=1; j<=N; j++) d[N+1][j] = d[N][j]; d[0][0] = d[1][1]; d[0][N+1] = d[0][N]; d[N][0] = d[N][1]; d[N+1][N+1] = d[N][N]; } function flow_grids(u, v, d) { // semi-Lagrangian method for (let i=1; i<=N; i++) { for (let j=1; j<=N; j++) { // 格子中央的速度 var cu = (u[i-1][j] + u[i][j]) / 2; var cv = (v[i][j-1] + v[i][j]) / 2; // 出發點 var x = i - 0.5 - cu * dt * speed; var y = j - 0.5 - cv * dt * speed; // 出發點必須在牆內 if (x < 0) x = 0; if (x > N) x = N; if (y < 0) y = 0; if (y > N) y = N; // 往前取值 d0[i][j] = interpolate(d, x + 0.5, y + 0.5); } } // [d, d0] = [d0, d]; // javascript pass by value // swap after calling function } function interpolate(a, x, y) { // bilinear interpolation var x0 = x | 0; var x1 = x0 + 1; var y0 = y | 0; var y1 = y0 + 1; var s1 = x - x0; var s0 = 1 - s1; var t1 = y - y0; var t0 = 1 - t1; return s0 * (t0 * a[x0][y0] + t1 * a[x0][y1]) + s1 * (t0 * a[x1][y0] + t1 * a[x1][y1]); }

補充說明：步幅增長

先前章節，計算速度場，避免增長步幅，以滿足CFL condition；繪製速度場，作弊增長步幅，以便讓動畫順暢。然而此舉導致繪圖結果不符合真實流體。

事實上，計算速度場，可以增長步幅，但是必須改變擴散與流動的演算法。請見這篇文章。

function interior() { diffuse(u, v); // 先擴散，讓牆壁速度能夠影響鄰水速度 flow(u, v); // 再流動 }

步幅。計算速度場、繪製速度場，步幅一致，不必作弊。

const h = 1; // 調大。移動距離較遠。 const dt = 1; // 調大。移動距離較遠。 const nu = 0.1; // 相對地調小。流體黏稠，減少影響範圍。 //const speed = 1000; // 步幅一致，不必作弊。

擴散。速度向四周擴散。

數學術語是implicit Euler method。

// 我很懶惰，沒有使用SOR和PCG，而是使用Jacobi method。 const diffusion = dt*nu/h/h; const iteration = 100; function diffuse(u, v) { copy(u0, u); copy(v0, v); for (let k=0; k<iteration; k++) { for (let i=1; i<=N-1; i++) for (let j=1; j<=N; j++) { var sum = u[i-1][j] + u[i+1][j] + u[i][j-1] + u[i][j+1]; u[i][j] = (u0[i][j] + diffusion * sum) / (1 + 4 * diffusion); } for (let i=1; i<=N; i++) for (let j=1; j<=N-1; j++) { var sum = v[i-1][j] + v[i+1][j] + v[i][j-1] + v[i][j+1]; v[i][j] = (v0[i][j] + diffusion * sum) / (1 + 4 * diffusion); } } }

流動。粒子數量場沿著速度場跑，速度場也跟著一起跑。

數學術語是semi-Lagrangian method。

function flow(u, v, d) { // u-velocity for (let i=1; i<=N-1; i++) for (let j=1; j<=N; j++) { var cv = (v[i][j-1] + v[i][j] + v[i+1][j-1] + v[i+1][j]) / 4; var x = i - u[i][j] * dt; var y = j - 0.5 - cv * dt; if (x < 0) x = 0; if (x >= N) x = N - 1e-6; if (y < 0) y = 0; if (y > N) y = N; u0[i][j] = interpolate(u, x, y + 0.5); } // [u, u0] = [u0, u]; // javascript pass by value // swap after calling function // v-velocity for (let i=1; i<=N; i++) for (let j=1; j<=N-1; j++) { var cu = (u[i-1][j] + u[i-1][j+1] + u[i][j] + u[i][j+1]) / 4; var x = i - 0.5 - cu * dt; var y = j - v[i][j] * dt; if (x < 0) x = 0; if (x > N) x = N; if (y < 0) y = 0; if (y >= N) y = N - 1e-6; v0[i][j] = interpolate(v, x + 0.5, y); } // [v, v0] = [v0, v]; // javascript pass by value // swap after calling function // density for (let i=1; i<=N; i++) { for (let j=1; j<=N; j++) { var cu = (u[i-1][j] + u[i][j]) / 2; var cv = (v[i][j-1] + v[i][j]) / 2; var x = i - 0.5 - cu * dt; var y = j - 0.5 - cv * dt; if (x < 0) x = 0; if (x > N) x = N; if (y < 0) y = 0; if (y > N) y = N; d0[i][j] = interpolate(d, x + 0.5, y + 0.5); } } // [d, d0] = [d0, d]; // javascript pass by value // swap after calling function }

守恆。Δt變大，流動之後誤差變大，各個物理量不再守恆。必須校正速度場，令物理量守恆。兩種方法。

質量守恆：流動前後，粒子數量總和不變。
動量守恆：流動前後，粒子動量總和不變。
能量守恆：流動前後，粒子動能總和不變。

projection method
1. flow，走一步。V1 = V0 + V0 ⋅ Δt
2. project，減掉散場。V1p = V1 - div_part(V1)

reflection method [Zehnder et al 2018]
1. flow，走半步。V½ = V0 + V0 ⋅ ½Δt
2. project，減掉散場。V½p = V½ - div_part(V½)
3. reflect，再減掉一次散場。V½r = V½ - div_part(V½) - div_part(V½)
4. flow，走半步。V1 = V½r + V½p ⋅ ½Δt
5. project，減掉散場。V1p = V1 - div_part(V1)

校正。Δt變大，流動之後誤差變大。有人校正速度場。

modified MacCormack method
1. 更新速度場。V0 -> V1
2. 速度變號，再更新速度場。V1 -> V2
   理論上回復原狀：V0 = V2
   實際上產生誤差：V0 ≠ V2
3. 來回更新兩次，因此更新一次的誤差是一半：(V2 - V0) / 2
4. 正確答案是更新一次，再扣掉更新一次的誤差：V1 - (V2 - V0) / 2
5. 裁切答案，不超過V1四周的最大值和最小值。

格：空氣與水

模擬流程。源自這個專案、這份講義、這套教材。

function update() { redistance(d); // air/water distance air(u, v, d); // air velocity boundary(u, v, d); // wall velocity water(u, v, d); // water velocity project(u, v, d); } function water(u, v, d) { diffuse(u, v, d); flow(u, v, d); gravity(u, v, d); }

水域。以粒或格，紀錄水域資訊，沿著速度場跑。四種解法。

marker particles
水域建立排列整齊的大量粒子，沿著速度場跑。
檢查每一格，若格中駐留足夠粒子，則視作水域。
粒子流動，間距改變，需要重置粒子。

front tracking
水面建立網格，沿著速度場跑。
網格流動，間距改變，需要修正網格。
間距太近則刪除一點，間距太遠則插入新點。

volume of fluid
建立水量場，沿著速度場跑。
格子流動，水量分配給目的地周遭四格，根據面積比例。

level set
水面到格子的距離，建立距離場，沿著速度場跑。
距離場流動，距離必錯，需要修正距離場。
重新估計水面位置，重新計算水面到格子的距離。

此處採用level set。建立距離場，水中為負值，水外為正值，水面為零。

我的實作，牆壁的距離值設為半格寬度。我沒查到相關資料。

// level set var d = new Float32Array2D(N+2, N+2); var d0 = new Float32Array2D(N+2, N+2); // temp init_distance(d); function init_distance(d) { // 通通沒水 for (let i=1; i<=N; i++) for (let j=1; j<=N; j++) d[i][j] = +1; // 長方形水域 for (let i=5; i<=N-5; i++) for (let j=10; j<=N-10; j++) d[i][j] = -1; // 牆壁 for (let i=1; i<=N; i++) d[i][0] = +0.5; for (let i=1; i<=N; i++) d[i][N+1] = +0.5; for (let j=1; j<=N; j++) d[0][j] = +0.5; for (let j=1; j<=N; j++) d[N+1][j] = +0.5; d[0][0] = d[0][N+1] = Math.sqrt(2) / 2; d[N][0] = d[N+1][N+1] = Math.sqrt(2) / 2; }

重算距離場。兩個步驟。

水面：距離異號的相鄰兩格，做一次內插，找到距離為零之處。
水內水外：從水面開始BFS遍歷每一格，並且計算距離。
　　　　　八鄰居取距離最小者，只取已有距離的格子。

我的實作，牆壁與水沒有做一次內插。我沒查到相關資料。

const dir8 = [[-1,-1],[-1,0],[-1,1],[0,1], [1,1],[1,0],[1,-1],[0,-1]]; var posx = new Float32Array2D(N+2, N+2); var posy = new Float32Array2D(N+2, N+2); var visit = new Float32Array2D(N+2, N+2); var estimate = new Float32Array2D(N+2, N+2); function redistance(d) { function cmp(a, b) {return d[a[0]][a[1]] - d[b[0]][b[1]];} var queue = new TinyQueue([], cmp); fill(visit, false); fill(estimate, false); // surface distance for (let i=1; i<=N; i++) for (let j=1; j<=N; j++) { // find zero contour var pos = new Array(8); for (let k=0; k<8; ++k) { var ni = i + dir8[k][0]; var nj = j + dir8[k][1]; if (!(ni>=1 && ni<=N && nj>=1 && nj<=N)) continue; var d1 = d[i][j]; var d2 = d[ni][nj]; if (d1 * d2 < 0) { var w = d1 / (d1 - d2); pos[k] = [(1-w)*i + w*ni, (1-w)*j + w*nj]; } } // distance to zero contour: two neighbor var mind = 1e9; for (let k=0; k<8; ++k) for (let l=1; l<=2; ++l) { if (!pos[k]) continue; if (!pos[(k+l)%8]) continue; var [x1,y1] = pos[k]; var [x2,y2] = pos[(k+l)%8]; // project point (i,j) onto segment x1->x2 var s = ((i-x1)*(x2-x1) + (j-y1)*(y2-y1)) / ((x2-x1)*(x2-x1) + (y2-y1)*(y2-y1)); s = Math.min(Math.max(s, 0), 1); var x = x1 + s * (x2-x1); var y = y1 + s * (y2-y1); var dist = Math.hypot(i-x, j-y); if (dist < mind) { mind = dist; posx[i][j] = x; posy[i][j] = y; dist = Math.max(dist, 1e-6); // prevent zero d[i][j] = (d[i][j] > 0 ? +1 : -1) * dist; } } // distance to zero contour: one neighbor for (let k=0; k<8; ++k) { if (pos[k] == null) continue; var dist = Math.hypot(pos[k][0] - i, pos[k][1] - j); if (dist < mind) { mind = dist; posx[i][j] = pos[k][0]; posy[i][j] = pos[k][1]; dist = Math.max(dist, 1e-6); // prevent zero d[i][j] = (d[i][j] > 0 ? +1 : -1) * dist; } } if (mind < 1e9) { queue.push([i,j]); visit[i][j] = true; } } // air distance + water distance while (queue.length > 0) { var [i,j] = queue.pop(); visit[i][j] = true; for (let dir of dir8) { var ni = i + dir[0]; var nj = j + dir[1]; if (!(ni>=1 && ni<=N && nj>=1 && nj<=N)) continue; if (!estimate[ni][nj] && !visit[ni][nj]) { if (estimate_distance(d, ni, nj)) { estimate[ni][nj] = true; queue.push([ni,nj]); } } } } } function estimate_distance(d, i, j) { var sign = (d[i][j] > 0 ? +1 : -1); var mind = 1e9; for (let dir of dir8) { var ni = i + dir[0]; var nj = j + dir[1]; if (visit[ni][nj]) { var dist = Math.hypot(posx[ni][nj] - i, posy[ni][nj] - j); if (dist < mind) { mind = dist; posx[i][j] = posx[ni][nj]; posy[i][j] = posy[ni][nj]; d[i][j] = sign * dist; } } } return mind < 1e9; }

外插。如果採用倒退步法，則空氣必須有速度，而水才能流入空氣。故以水域速度設定空氣速度。兩種解法。

最短距離：找到距離最近的水面格子，速度設成相同。
逐層擴散：從水面開始，一層層設定速度。
　　　　　八鄰居的速度平均數，只取已有速度的格子。

我的實作，距離場的計算順序不正確。既不是最短路徑Dijkstra's algorithm，也不是逐層設定BFS。導致速度外插有時候優先遭遇距離較小、但是離水面較遠的孤立格子。目前的應急措施是塞回queue。

var uc = new Float32Array2D(N+2, N+2); var vc = new Float32Array2D(N+2, N+2); function air(u, v, d) { // 格子中心速度 for (let i=1; i<=N; ++i) for (let j=1; j<=N; ++j) uc[i][j] = (u[i-1][j] + u[i][j]) / 2 for (let i=1; i<=N; ++i) for (let j=1; j<=N; ++j) vc[i][j] = (v[i][j-1] + v[i][j]) / 2 // bfs fill(visit, false); // push air to queue var queue = []; for (let i=1; i<=N; i++) for (let j=1; j<=N; j++) if (d[i][j] < 0) visit[i][j] = true; else queue.push([i,j]); // sort by distance function cmp(a, b) {return d[a[0]][a[1]] - d[b[0]][b[1]];} queue.sort(cmp); // BFS，從水面往外，逐層擴散，一層層設定空氣速度。 while (queue.length > 0) { [i,j] = queue.shift(); visit[i][j] = true; var usum = 0, vsum = 0, csum = 0; for (let dir of dir8) { var ni = i + dir[0]; var nj = j + dir[1]; if (visit[ni][nj]) { usum += uc[ni][nj]; vsum += vc[ni][nj]; csum ++; } } // 八鄰居的速度平均數，只取已有速度的格子。 if (csum > 0) { uc[i][j] = usum / csum; vc[i][j] = vsum / csum; } else { queue.push([i,j]); } } // 格子中心速度還原成格子邊界速度 for (let i=1; i<=N-1; ++i) for (let j=1; j<=N; ++j) u[i][j] = (uc[i+1][j] + uc[i][j]) / 2; for (let i=1; i<=N; ++i) for (let j=1; j<=N-1; ++j) v[i][j] = (vc[i][j+1] + vc[i][j]) / 2; }

不可壓縮。水域才投影，水外不必投影。

function project(u, v) { // get divergence (without dividing h) fill(div, 0); // 補零 for (let i=1; i<=N; ++i) for (let j=1; j<=N; ++j) if (d[i][j] < 0) // 水域才求解 div[i][j] = u[i][j] - u[i-1][j] + v[i][j] - v[i][j-1]; // solve for pressure (without dividing h) solve(p, div); // remove divergence field for (let i=1; i<=N-1; ++i) for (let j=1; j<=N; ++j) u[i][j] -= (dt/h)*(p[i+1][j]-p[i][j]); for (let i=1; i<=N; ++i) for (let j=1; j<=N-1; ++j) v[i][j] -= (dt/h)*(p[i][j+1]-p[i][j]); }

求解。水域才求解，水外不必求解。空氣壓力為零，須採計。

牆壁速度：方便起見設為鄰水速度外插。　理論上是零。
空氣速度：方便起見設為水面速度外插。　理論上是零。
牆壁壓力：不計，方便起見設為零。　　　理論上是水壓：水深乘以密度。
空氣壓力：採計，方便起見設為零。　　　理論上是一大氣壓。

// successive over-relaxation const beta = 1.2; const iteration = 100; function solve(p, div) { fill(p, 0); // wall/air pressure is zero for (let k=0; k<iteration; ++k) { for (let i=1; i<=N; ++i) for (let j=1; j<=N; ++j) if (d[i][j] < 0) { // 水域才求解 var sum = p[i+1][j] + p[i-1][j] + p[i][j+1] + p[i][j-1]; p[i][j] = beta*(sum-(h/dt)*div[i][j])/c[i][j] + (1-beta)*p[i][j]; } } } // preconditioned conjugate gradient var M = new Float32Array2D(N+2, N+2); var r = new Float32Array2D(N+2, N+2); var s = new Float32Array2D(N+2, N+2); var z = new Float32Array2D(N+2, N+2); var q = new Float32Array2D(N+2, N+2); // 跟之前一樣 function solve(x, b) { fill(p, 0); // x = 0 if (dot(b, b) < 1e-6) return; // b == 0 copy(r, b); // r = b negate(r); // r = -b buildPreconditioner(M); applyPreconditioner(M, r, z); // z = f(r) var a = dot(z, r); // a = z . r for (let k=0; k<N*N; k++) { copy(s, z); // s = z compute_Ax(s, z); // z = A(s) var alpha = a / dot(z, s); add(x, s, +alpha); // x += alpha * s add(r, z, -alpha); // r -= alpha * z var e = dot(r, r); // e = r . r if (e/(N*N) < 1e-6) break; applyPreconditioner(M, r, z); // z = f(r) var anew = dot(z, r); // anew = z . r var beta = anew / a; add(z, s, +beta); // z += beta * s a = anew; } } // 判斷水域。水域為1，否則為0。 function sgn(i, j) { return (i>=1 && i<=N && j>=1 && j<=N) && d[i][j] < 0; } // modified incomplete Cholesky preconditioner function buildPreconditioner(M) { const tau = 0.97; fill(M, 0); // 補零 for (let i=1; i<=N; ++i) for (let j=1; j<=N; ++j) { if (d[i][j] < 0) { // 水域才求解 var ai = sgn(i-1,j) * M[i-1][j] * M[i-1][j]; var aj = sgn(i,j-1) * M[i][j-1] * M[i][j-1]; var e = c[i][j] - (1 - tau) * (ai + aj); M[i][j] = 1 / Math.sqrt(e + 1e-6); } } } function applyPreconditioner(M, r, z) { // Lq = r fill(q, 0); // 補零 for (let i=1; i<=N; ++i) for (let j=1; j<=N; ++j) { if (d[i][j] < 0) { // 水域才求解 var ai = sgn(i-1,j) * M[i-1][j] * q[i-1][j]; var aj = sgn(i,j-1) * M[i][j-1] * q[i][j-1]; q[i][j] = (r[i][j] + ai + aj) * M[i][j]; } } // Lᵀz = q fill(z, 0); // 補零 for (let i=N; i>=1; --i) for (let j=N; j>=1; --j) { if (d[i][j] < 0) { // 水域才求解 var ai = sgn(i+1,j) * M[i][j] * z[i+1][j]; var aj = sgn(i,j+1) * M[i][j] * z[i][j+1]; z[i][j] = (q[i][j] + ai + aj) * M[i][j]; } } } // y = Ax function compute_Ax(x, y) { fill(y, 0); // 補零 for (let i=1; i<=N; ++i) for (let j=1; j<=N; ++j) { if (d[i][j] < 0) { // 水域才求解 var sum = x[i+1][j] + x[i-1][j] + x[i][j+1] + x[i][j-1]; y[i][j] = (c[i][j] * x[i][j] - sum) * (dt/h); } } }

重力。垂直速度，添加常數。

const g = 0.3; // 重力加速度 function gravity(u, v, d) { for (let i=1; i<=N; ++i) for (let j=1; j<=N-1; ++j) if (d[i][j] < 0 || d[i][j+1] < 0) v[i][j] += g * dt; }

補充說明：redistance

redistance可以跟project並排，視作距離場校正。redistance也可以跟air並排，視作距離場外插，視作flow的事前準備工作。我覺得後者是比較好的。以程式碼結構來說，速度場外插和距離場外插是可以合併一起做的。

補充說明：multigrid level set

level set是舊方法了。有個新方法是multigrid level set。請參考《Real-Time Eulerian Water Simulation Using a Restricted Tall Cell Grid》。然而這是NVIDIA的專利。

補充說明：advect命名錯誤

許多流體模擬文獻，flow誤植為advect，流動誤認為平流。

flow是流動（連續方程式）。project讓流動變得不可壓縮。advect是平流（平流方程式）。flow和project合體才是advect。

微觀與宏觀

粒：壓縮力、黏滯力。格：擴散、流動、不可壓縮。

粒微觀，格宏觀。有趣的是，迄今無人發現微觀與宏觀之間的數學關係式。

擴散包含了壓縮力和黏滯力。然而大家習慣將擴散視作黏滯，將雷諾數視作黏滯程度。雖然不完全正確，但是容易理解。

以下方程式皆是宏觀觀點。

continuity equation

連續方程式。描述流動守恆的方程式。一個地點的物理量之所以增加減少，是因為跟隔壁跑來跑去。不會無中生有，不會無端消失。

時間變化。這個時刻、上個時刻的物理量差距。

物理量可以是質量、體積、力、………。

∂   
—— q                               ---> q̇
∂t  

空間變化。這個地點、隔壁地點的物理量差距。考慮流動速度。

物理量必須適合各維度加總，例如質量、體積、………。

∂        ∂     
—— qv  + —— qv                     ---> div(qv)
∂x   ˣ   ∂y   ʸ

連續方程式。時間變化＝空間變化。

∂        ∂        ∂           
—— q + ( —— qv  + —— qv  ) = 0     ---> q̇ + div(qv) = 0
∂t       ∂x   ˣ   ∂y   ʸ      
^^^^   ^^^^^^^^^^^^^^^^^^^
temporal  spatial change
change

advection equation

平流方程式。水位差距與流量成正比。水位差距會移動。

連續方程式，拆成平流與壓縮。

函數乘法的微分公式：前微後不微、前不微後微。

∂           ∂         ∂            ∂       ∂          
—— q + ( v  —— q + v  —— q ) + q ( —— v  + —— v  ) = 0
∂t        ˣ ∂x      ʸ ∂y           ∂x  ˣ   ∂y  ʸ      
       ^^^^^^^^^^^^^^^^^^^^^   ^^^^^^^^^^^^^^^^^^^
       advection               compression

平流。物理量往隔壁流動，差距越大，流量越大。

     ∂         ∂     
( v  —— q + v  —— q )              ---> v dot grad(q)
   ˣ ∂x      ʸ ∂y    

壓縮。物理量聚集或者散開。

    ∂       ∂      
q ( —— v  + —— v  )                ---> q div(v)
    ∂x  ˣ   ∂y  ʸ  

不可壓縮。壓縮項為零，速度的散度為零。速度出入總量相等，不生不滅；物質流動順暢，不推不擠。

    ∂       ∂      
q ( —— v  + —— v  ) = 0            ---> q div(v) = 0
    ∂x  ˣ   ∂y  ʸ  

平流方程式。時間變化＝平流。

∂           ∂         ∂         
—— q + ( v  —— q + v  —— q ) = 0   ---> q̇ + (v dot grad(q)) = 0
∂t        ˣ ∂x      ʸ ∂y        
^^^^   ^^^^^^^^^^^^^^^^^^^^^
temporal    advection
change

有人簡寫成大寫D，稱為「物質導數」。

D       
—— q = 0
Dt      

hydrodynamic equation

流體方程組。三種式子同時聯立。請見教學網頁、教學講義。

一、密度：連續方程式。

時間變化＝空間變化。

∂        ∂        ∂           
—— ρ + ( —— ρv  + —— ρv  ) = 0     ---> ρ̇ + div(ρv) = 0
∂t       ∂x   ˣ   ∂y   ʸ      

二、動量密度：連續方程式，追加兩種力。

時間變化＋空間變化＝零階位勢（壓力）＋二階位勢（應力）。

∂          ∂         ∂            ∂        ∂        ∂           
—— ρv  + ( —— ρv v + —— ρv v  ) + —— p + ( —— σ   + —— σ   ) = 0
∂t   ˣ     ∂x   ˣ ˣ  ∂y   ˣ ʸ     ∂x       ∂x  ˣˣ   ∂y  ˣʸ      

∂          ∂         ∂            ∂        ∂        ∂           
—— ρv  + ( —— ρv v + —— ρv v  ) + —— p + ( —— σ   + —— σ   ) = 0
∂t   ʸ     ∂x   ʸ ˣ  ∂y   ʸ ʸ     ∂y       ∂x  ʸˣ   ∂y  ʸʸ      
^^^^^^   ^^^^^^^^^^^^^^^^^^^^^^   ^^^^   ^^^^^^^^^^^^^^^^^^^
temporal spatial                  order-0     order-2
change   change                   potential   potential

         ---> ∂(ρv)/∂t + div(ρv tensor v) + grad(p) + div(σ) = 0

三、能量密度：我不熟悉，就不講了。

Navier–Stokes equation

水是流體的特例。因此方程組可以簡化。

一、水滿足牛頓黏滯定律：應力與速度梯度成正比。

因此應力簡化成擴散。

  ∂        ∂     
  —— σ   + —— σ  
  ∂x  ˣˣ   ∂y  ˣʸ

  ∂       ∂         ∂       ∂      
= —— ( -μ —— v  ) + —— ( -μ —— v  )
  ∂x      ∂x  ˣ     ∂y      ∂y  ˣ  

       ∂        ∂       
= -μ ( ——— v  + ——— v  )         ---> -μ laplace(v)
       ∂x²  ˣ   ∂y²  ˣ  

二、水幾乎不可壓縮：速度散度為零。

因此空間變化簡化成平流。

  ∂          ∂       
  —— ρv v  + —— ρv v 
  ∂x   ˣ ˣ   ∂y   ˣ ʸ
  ^^^^^^^^^^^^^^^^^^^
   space difference

       ∂           ∂                ∂       ∂      
= ( v  —— ρv  + v  —— ρv  ) + ρv  ( —— v  + —— v  )
     ˣ ∂x   ˣ    ʸ ∂y   ˣ       ˣ   ∂x  ˣ   ∂y  ʸ  
  ^^^^^^^^^^^^^^^^^^^^^^^^^   ^^^^^^^^^^^^^^^^^^^^^
  advection                   compression = 0

       ∂           ∂       
= ( v  —— ρv  + v  —— ρv  )     ---> v dot grad(ρv)
     ˣ ∂x   ˣ    ʸ ∂y   ˣ   

三、水幾乎密度均勻不變：密度是常數。

因此時空變化可以一併提出密度。

  ∂             ∂           ∂       
  —— ρv  + ( v  —— ρv  + v  —— ρv  )
  ∂t   ˣ      ˣ ∂x   ˣ    ʸ ∂y   ˣ  

      ∂            ∂          ∂        
= ρ ( —— v  + ( v  —— v  + v  —— v  ) )
      ∂t  ˣ      ˣ ∂x  ˣ    ʸ ∂y  ˣ    

    ---> ρ ( v̇ + (v dot grad(v)) )

Navier–Stokes equation。教科書通常只介紹它。

⎰ ρ ( v̇ + (v dot grad(v)) ) + grad(p) - μ laplace(v) = 0
⎱ div(v) = 0

⎰ ρ ( v̇ + (v ∙ ∇v) ) + ∇p - μ ∇∙∇v = 0
⎱ ∇∙v = 0

⎰ v̇ + (v ∙ ∇v) + (∇p / ρ) - ν ∇∙∇v = 0    (let μ / ρ = ν)
⎱ ∇∙v = 0                   ^^nu                       ^^nu

Navier–Stokes equation for 2D water

水的Navier–Stokes equation，二維的情況下，有兩種形式。

一、壓力與速度（原式）：可精確模擬層流。

pressure-velocity formulation
⎰ v̇ + (v dot grad(v)) + (grad(p) / ρ) - ν laplace(v) = 0
⎱ div(v) = 0

二、流函數與渦旋：可精確模擬亂流。例如自然現象leapfrogging vortex ring、microburst。

streamfunction-vorticity formulation
⎰ ω̇ - (grad(ψ) cross grad(ω)) - ν laplace(ω) = 0
⎱ laplace(ψ) = -ω

推導過程請見這篇講義。原式套用旋度，速度改成位勢。

Schrödinger equation for water

計算幾何有個手法，讓實數變複數：二維座標(x,y)改成複數x+y𝑖，二維座標平移、縮放、旋轉改成複數加法、倍率、乘法。

流體力學也有個手法，讓實數變複數：hydrodynamic equation改成Schrödinger equation，三維實數改成二維複數，質量（密度）改成複數長度平方，速度改成複數角度。請見這篇論文。

hydrodynamic equation速度平流形式

流體方程組（省略能量密度）有兩種形式。

此處補上零階位勢（重力）。並且採用精煉的數學符號。

第一種形式：密度連續方程式、動量密度連續方程式。

⎧ ∂
⎪ —— ρ + ∇∙(ρv) = 0                     conservation of mass
⎪ ∂t
⎨ 
⎪ ∂
⎪ —— ρv + ∇∙(ρv⊗v) + ρg + ∇p + ∇∙σ = 0  conservation of momentum
⎩ ∂t

第二種形式：密度連續方程式、速度平流方程式。

⎧ ∂
⎪ —— ρ + ∇∙(ρv) = 0                     conservation of mass
⎪ ∂t
⎨ 
⎪ D          ∇p    ∇∙σ
⎪ —— v + g + ——— + ——— = 0              advection of velocity
⎩ Dt          ρ     ρ

第一種形式到第二種形式的推導過程：

derivation from first equation to second equation:

∂       ⎛ ∂    ⎞     ⎛ ∂    ⎞
—— ρv = ⎜ —— ρ ⎟v + ρ⎜ —— v ⎟         1st term of
∂t      ⎝ ∂t   ⎠     ⎝ ∂t   ⎠         conservation of momentum
        ^^^^^^^^(a)

∇∙(ρv⊗v) = (∇∙(ρv))v + (ρv)∙∇v        2nd term of
           ^^^^^^^^(b)                conservation of momentum

(a) + (b) = 0                         conservation of mass

  ∂
ρ —— v + (ρv)∙∇v + ρg + ∇p + ∇∙σ = 0  conservation of momentum
  ∂t                                  since (a) + (b) = 0

 ⎛ ∂           ⎞
ρ⎜ —— v + v∙∇v ⎟ + ρg + ∇p + ∇∙σ = 0
 ⎝ ∂t          ⎠

  D  
ρ —— v + ρg + ∇p + ∇∙σ = 0            material derivative
  Dt 

第一種形式，連續＝平流＋壓縮。不可壓縮則剩下平流。動量密度平流。

第二種形式，可以壓縮、不可壓縮，一律得到速度平流。

注意到，每當遇到速度平流，也許可以壓縮，也許不可壓縮！如果不可壓縮，必須特地寫出、同時聯立。這是常見誤區。

material derivative

二維曲線。輸入是時間t，輸出是x座標、y座標。

⎰ x(t)
⎱ y(t)

沿著路徑的函數。輸入是位置(x(t), y(t))。

q(x(t), y(t))

拉格朗日描述。輸入是位置(x(t), y(t))、時間t。

曲線自身相交（不同時間卻有相同位置）能被分辨了。

q(x(t), y(t), t)

物質導數。拉格朗日描述對時間t微分。

多變數函數複合的微分公式：偏微分、連鎖律、相加。

D      d      ∂q dx   ∂q dy   ∂q dt
—— q = —— q = —— —— + —— —— + —— ——
Dt     dt     ∂x dt   ∂y dt   ∂t dt

              ∂q      ∂q      ∂q
            = —— v  + —— v  + ——      ---> (grad(q) dot v) + q̇
              ∂x  ˣ   ∂y  ʸ   ∂t
 
where q has the form of q(x(t), y(t), t)

拉格朗日描述只能處理平流，歐拉描述則可以處理平流與壓縮。古人沒有意識到這件事情，而將物質導數誤植為主角，導致敘事結構混亂，成為歷史共業。

關鍵字一覽

目前有非常多事情等人去做。

粒子間作用力　　Lennard–Jones potential、intermolecular force
內聚力、附著力　cohesion、adhesion
浮力、摩擦力　　buoyancy、friction
升力、降力　　　lift、downforce
推力、牽引力　　thrust、traction
障礙物　　　　　immersed boundary method、Werner–Wengle wall function
多相流　　　　　multiphase flow
交融　　　　　　Rayleigh–Taylor instability、Kelvin–Helmholtz instability
層流、亂流　　　laminar、turbulence (mean + fluctuation)
無因次量　　　　Reynolds number、Froude number
溫度、能量　　　temperature、energy
角動量　　　　　angular monentum、vorticity、helicity
底形　　　　　　bedform
氣泡流、氣塊流　bubble flow、slug flow
顆粒流　　　　　granular flow

water wave

water spike wave

water flow

instability

soft body simulation（deformable body simulation）

柔體模擬。物質具備特定造型，物質可以平移旋轉縮放。

對應到連體力學之固體力學。

資源

Ten Minute Physics
https://www.math.ucla.edu/~cffjiang/
https://www.math.ucdavis.edu/~jteran/
https://en.wikipedia.org/wiki/Soft-body_dynamics
https://www.comsol.com/multiphysics/introduction-to-structural-mechanics

spring network model

矩形網格。點是粒子，邊是彈簧。

避免塌陷、避免摺疊，只好添加對角線彈簧、兩格寬彈簧。

粒子移動，不得穿越粒子，否則粒子可能高速噴射。針對一個粒子，彈簧越多，合力越大，速度越快，移動越遠。小心調整彈性係數，避免粒子高速噴射。

小心調整阻尼係數，避免彈簧振動不止。

spring network model改良版本

模擬流程源自這個專案。我印象中這是遊戲開發者大會GDC的一篇報告，然而我現在找不到了。如果你知道出處，麻煩告訴我。

一、縮放彈簧。粒子伸出堅固拉桿，長度是半格。彈簧綁在拉桿末端，長度是零。粒子運動，拉桿隨之運動，彈簧隨之伸長。拉桿末端位置差異，作為彈簧伸長長度，用來計算彈簧力。簡單起見，XY兩個維度的伸長長度，分別計算彈簧力分量。

縮放彈簧除了產生力，也產生力矩（力臂是拉桿長度）。力矩可以避免塌陷、避免摺疊。不必添加對角線彈簧、兩格寬彈簧。

二、阻尼。粒子擁有平移速度和旋轉速度。仿照剛體，計算彈簧中央速度。兩個相鄰粒子於彈簧中央的速度差異，用於計算阻尼力與阻尼力矩。

三、旋轉彈簧。粒子旋轉角度，作為彈簧伸長長度，用來計算彈簧力。

改良版本，物體更柔軟。放棄部分畫面，可讓物體看起來變得堅固。換句話說，粒子移動數次，才繪圖一次。

shape matching model

《Meshless Deformations Based on Shape Matching》

然而這是NVIDIA的專利。按理來說，我不可以介紹。

《FastLSM: Fast Lattice Shape Matching for Robust Real-Time Deformation》

一、各點分開處理。針對一個點，找到鄰近的點，形成群。即是meshfree discretization。然而本質仍是網格：邊連往鄰近的點。

二、各群分開處理。針對一個群，觀察初始位置、當前位置。找到平方誤差最小的旋轉矩陣（剛體變換）。使用Kabsch–Umeyama algorithm得到旋轉矩陣（維度的協方差矩陣的極分解）。群內各點實施旋轉，得到新位置。

三、各點分開處理。針對一個點，鄰近的群各自擁有該點新位置，取平均數作為該點新位置。

四、再使用Verlet method得到新速度。或者更進一步，新速度乘上自訂係數（堅固係數），加入到原速度。或者換句話說，原位置與新位置的差距，視作彈簧力。

五、各點移動。加速度ｘ時間＝速度。速度ｘ時間＝移動距離。

小心調整彈性係數，避免粒子高速噴射。

小心調整阻尼係數，避免彈簧振動不止。

我的實作當中，沒有仔細調整彈性係數。掄牆時，外力與彈簧力總和偶爾過大，導致粒子高速噴射。

原始論文並未提及阻尼力。事實上此方法難以設計阻尼力。我的實作當中，自行設計阻尼力，但是效果極差，甚至阻礙自由落體。

此方法大致上就是rigid deformation的「點變換、邊誤差」，重心到各個點當作邊。

shape matching model改良版本

《Position-Based Dynamics》

《Physically Based Shape Matching》

第一篇是原型。第二篇引入了彈性模型。

然而這是NVIDIA的專利。該公司的遊戲物理引擎PhysX基於此方法。按理來說，我不可以介紹。我打算等到專利過期。你可以等待作者親自介紹。

elastic deformation = Laplacian preserving ?

spring network model是邊平方總和盡量小（彈性位能盡量小），即是Laplace–Beltrami operator = 0，即是harmonic。

shape matching model是邊平方誤差盡量小，即是Laplace–Beltrami operator盡量保持相同，即是Laplacian preserving。

數學之微分幾何的Laplacian preserving、物理學之連體力學的elastic deformation，我不清楚兩者有何關聯，但是我認為肯定有所關聯。麻煩各位趕快發表論文吧。

最佳化與物體穩態

能量對位置微分是力。dE/dx = F。

物理　　丨數學　　
一一一一十一一一一一一一一一一一一一一一一
力　　　丨向量　　
能量　　丨二次型（凸函數，擁有唯一最小值）
一一一一十一一一一一一一一一一一一一一一一
合力　　丨向量相加
能量總和丨二次型相加
一一一一十一一一一一一一一一一一一一一一一
力￫￫能量丨積分
能量￫￫力丨微分／梯度　
一一一一十一一一一一一一一一一一一一一一一
穩態　　丨二次型函數極值

極值位於一次微分等於零的地方。

能量最小的位置，就是力等於零的位置。能量總和最小的位置，就是合力為零的位置。物理術語是穩態。

最佳化已有許多演算法。例如gradient descent：

設定物體位置（初始狀態）。朝著能量梯度方向走，修改位置。一步一步走向能量最小的位置（最終狀態）。

順帶一提，朝著能量梯度方向走，沿途經過的位置，不是真實的運動軌跡。梯度下降、運動軌跡，兩者無關。

能量的梯度是力。想要求得運動軌跡，必須以力求得加速度，再求得速度，再求得位置。然而這樣不再是梯度下降法，不再保證走向能量最小的位置。

實際應用諸如建築結構分析、化學結構分析。

structural optimization: topology optimization  調整模型結構
molecular modeling: energy minimization         調整化學結構

範例：大量彈簧靜力平衡

統計所有彈簧的彈性位能，求最小值所在位置（每個彈簧的端點座標）。梯度等於零，就是靜力平衡。就是穩態。

min sum ½ kᵢⱼ (‖xᵢ - xⱼ‖ - l₀ᵢⱼ)²
 x  i,j

½ k (l - l₀)²   彈性位能　　　
k (l - l₀)      彈簧力　　　　
l₀              彈簧預設長度　
l               彈簧目前長度　
k               彈性係數　　　
x               彈簧端點位置　

範例：大量剛體同時碰撞

p = mv --> w = Ax    衝量公式 Δp₂ = m₁₂* Δv₁₂
v      --> x         每個物體的速度（3n個數值，形成3n×1向量）
p      --> w         每個物體的衝量（3n個數值，形成3n×1向量）
m      --> A         物體兩兩之間的約化質量（n²個數值，形成3n×3n矩陣）
p = mv + fΔt --> w = Ax + b  考慮其他外力f

v ≥ 0  --> x ≥ 0     相對速度（>0分開 =0接觸 <0侵入）
p ≥ 0  --> w ≥ 0     衝量（再除以Δt得到力f）
pv = 0 --> wᵀx = 0   接觸時，無速度、有衝量
                     不接觸時，有速度、無衝量

solve wᵀx = 0  subject to x ≥ 0 and w ≥ 0
where w = Ax + b
where A is symmetric postive-semidefinite

這個東西怪怪的。我不太確定我的理解是否正確。

衝量公式。相對速度修改定義：朝外分開為正值，朝內侵入為負值。衝量修改定義：不可為負值。

問題宛如線性規劃，演算法宛如單形法。該問題稱作linear complementarity problem，其演算法稱作Lemke's algorithm。

《Nonlinear Programming: Theory and Algorithms》

最佳化與物體運動

利用約束最佳化，描述物體運動軌跡。

目標函數：物體先後位置差異。

約束條件：物理定律。

min ‖x' - x‖²  subject to c(x') = 0
 x'

min sum ‖xᵢ' - xᵢ‖²  subject to cⱼ(x₁', x₂', ..., xₙ') = 0
 x'  i

約束最佳化已有許多演算法。例如Lagrange multiplier：

約束最佳化問題，利用拉格朗日乘數λ，化作最佳化問題。再利用「極值位於一次微分等於零的地方」，化作求解問題。

（一次微分等於零的地方，不一定是極值。必須檢查。）

solve 2(x' - x) + λ ∇c(x') = 0

solve sum 2(xᵢ' - xᵢ) + sum λⱼ ∇cⱼ(x₁', x₂', ..., xₙ') = 0

約束最佳化已有許多演算法。例如project gradient method：

朝著目標函數的梯度方向走，再朝著約束函數的梯度方向走。兩者輪流，直到位置幾乎不變。

朝著約束函數的梯度方向走，可以一步到位（需要解方程式），也可以逐步前進（不需要解方程式）。

約束函數通常是能量。限制能量，即是施力。符合物理現象。

目標函數：新舊位置的距離平方。
目標函數的梯度：舊位置到新位置的向量。
朝著目標函數的梯度方向走一步：稍微回到舊位置。（朝梯度反方向，得極小值。）
約束函數：能量。
約束函數的梯度：力。
朝著約束函數的梯度方向走一步：施力並且運動。
兩者輪流，直到位置幾乎不變：遵循最小作用量原理，不斷嘗試，直到找到正確方向。

也有人發明新演算法《Position-Based Dynamics》，融合了約束最佳化演算法與運動模擬演算法。

然而這是NVIDIA的專利。將來應該會寫進教科書。

一、更新位置x。
　　x' = x + v Δt
二、projected gradient method：追加約束條件c(x) = 0，並且修正位置。
　　x" = solve(c, x')
三、Verlet method：新位置與舊位置差異，反推新速度v。
　　v' = (x" - x) / Δt

講個八卦。本章節這個手法，不斷獲得各種酷炫的名稱：

position based dynamics
projective dynamics
incremental potential contact
differentiable simulation

這個手法出處不明。我只知道《Computational Inelasticity》該書1.4.3.1節提到這個手法。

範例：大量彈簧連動

約束條件：能量守恆。動能加位能等於常數。

彈簧運動當中，限制能量，即是施加彈簧力。

min sum ‖xᵢ' - xᵢ‖²  subject to c(x₁', x₂', ..., xₙ') = E
 x'  i

c(x₁', x₂', ..., xₙ') = sum ½ mⱼ vⱼ'² + sum ½ kₖ (lₖ' - l₀ₖ)²
vⱼ' = (xⱼ' - xⱼ) / Δt
lₖ' = ‖xₖ₁' - xₖ₂'‖

範例：軌道運動

約束條件：能量守恆。動能加位能等於常數。

軌道運動當中，限制能量，即是施加向心力。

範例：剛體碰撞

約束條件：侵入距離大於等於零。

效果宛如彈簧力。

https://box2d.org/files/ErinCatto_UnderstandingConstraints_GDC2014.pdf
https://zhuanlan.zhihu.com/p/143003234 
https://zhuanlan.zhihu.com/p/396890810

範例：柔體運動

位置與速度盡量相同，能量必須固定。

min sum ‖xᵢ' - xᵢ‖² + ‖vᵢ' - vᵢ‖²  subject to c(x,v) = 0
x'v' i

x x'是先後位置，v v'是先後速度。c(x,v)是能量。

問題是二次規劃，演算法是Newton–Lagrange method與projected gradient method兩者併用。

qₖ₊₁ = argmin ½ ‖q - qₖ‖ᴅ²  subject to c(qₖ) + ∇c(qₖ)ᵀ(q - qₖ) = 0
         q
solve λₖ₊₁: [∇c(qₖ)ᵀ D⁻¹ ∇c(qₖ)] λₖ₊₁ = c(qₖ)
solve qₖ₊₁: qₖ₊₁ = qₖ - D⁻¹ ∇c(qₖ) λₖ₊₁

位置xᵢ和速度vᵢ的所有數值，拼成向量q。

《FEPR: Fast Energy Projection for Real-Time Simulation of Deformable Objects》

global solver / local solver

物體穩態表示成最佳化問題。極值位於一次微分等於零的地方。目標函數預先微分，化作求解問題。

物體運動表示成約束最佳化問題。極值位於一次微分等於零的地方。拉格朗日函數預先微分，化作求解問題。

物理學當中，大多數物理現象，習慣化作微分方程組。

計算學當中，利用離散化，進一步化作一次方程組。

各個粒／格，各自擁有線性方程式。我們可以合併求解或依序求解。

全域求解（合併求解）：所有方程式併成大型稀疏矩陣。實施矩陣求解演算法（高斯消去法、共軛梯度法），一口氣求得所有粒／格的物理量。

局部求解（依序求解）：每個方程式輪流求解。手工推導公式解（移項、配方法）。其他粒／格的物理量暫時視為已知，解出當前粒／格的物理量。反覆輪迴，直到收斂。

局部求解其實就是矩陣求解演算法之relaxation系列。（順帶一提，relaxation其實就是一種特殊的operator splitting。）

全域／局部其實就是矩陣求解演算法的差別。

kinematic constraint

運動約束。物體學家將約束條件做了分類。

    ┌ scleronomic constraint h(x₁,x₂,…) = 0           堅固約束
    ├ rheonomic constraint   h(x₁,x₂,…,t) = 0         流動約束
  ┌ holonomic constraint     h(x₁,x₂,…,t) = 0         完整約束
  ├ non-holonomic constraint h(x₁,x₂,…,ẋ₁,ẋ₂,…,t) = 0 非完整約束
┌ equality constraint        h(…) = 0                 等式約束
├ inequality constraint      h(…) ≥ 0                 不等式約束
kinematic constraint                                  運動約束

許多力學名詞的中文翻譯相當詭異，看起來像是惡作劇。

term                    丨中文　　　丨意譯　　丨意義
------------------------丨一一一一一丨一一一一丨一一一一一一一一一
mechanics               丨力學　　　丨機動學　丨機構作動的學問
├ kinematics            丨運動學　　丨運動學　丨運動的學問
├ statics               丨靜力學　　丨靜態學　丨運動未變化的學問
└ dynamics = kinetics   丨動力學　　丨動態學　丨運動有變化的學問
------------------------丨一一一一一丨一一一一丨一一一一一一一一一
mechanism               丨機構（學）丨機構　　丨機器結構
mechanical mechanics    丨機械力學　丨　　　　丨台灣原創詞彙，屌！
------------------------丨一一一一一丨一一一一丨一一一一一一一一一
holonomic constraint    丨完整約束　丨完整約束丨包含以下兩者
├ scleronomic constraint丨定常約束　丨堅固約束丨位置的限制
└ rheonomic constraint  丨非定常約束丨流動約束丨位置暨時間的限制

維基字典可以查到這些詞彙的歷史用法。可以查詢字首字根。

https://en.wiktionary.org/wiki/nomic
https://en.wiktionary.org/wiki/sclero-
https://en.wiktionary.org/wiki/rheo-
https://en.wiktionary.org/wiki/holo-

material point method

模擬流程源自這個專案、這本書籍、這段閒聊。

（物體裂開、粒子高速逸散，這是質點法的主要瑕疵。）

質點法細節豐富，我打算分段介紹。

material point method: basis interpolation

粒。每個粒子都有物理量。

格。每個格子都有物理量。

粒格轉換。採用basis interpolation。

一、每個粒／格各自散發力場，中央高外圍低。每個格／粒各自接收力場，加總數值。

二、為了省時，interpolation簡化為approximation，避免計算反矩陣。（答案不再精確。）

qᵢ = sum wᵢₚ qₚ     particle to grid
      ᵖ
qₚ = sum wᵢₚ qᵢ     grid to particle
      ⁱ
q: physical quantity (e.g. mass, volume, velocity, force)
p: particle index    (coordinates (x,y,z))
i: grid index        (coordinates ((i+½)Δx,(j+½)Δy,(k+½)Δz))
w: basis function
wᵢₚ: w(difference between grid i and particle p)

基底函數。採用B-spline。

一、為了連續，基底函數拓寬為1.5格寬、甚至2格寬，避免物體斷裂。

二、為了省時，基底函數簡化為separable function，避免計算平方根。（等高線不再是圓形。）

input standardization:

  ⎡x⎤      ⎡x/Δx⎤
w(⎢y⎥) = B(⎢y/Δy⎥)     [x y z]ᵀ is difference
  ⎣z⎦      ⎣z/Δz⎦      (Δx,Δy,Δz) is grid size

separable function:

  ⎡x⎤
B(⎢y⎥) = B(x)B(y)B(z)
  ⎣z⎦

quadratic B-spline:

       ⎧ 3/4 - |x|²        , 0   ≤ |x| < 1/2
B(x) = ⎨ 1/2 (3/2 - |x|)²  , 1/2 ≤ |x| < 3/2
       ⎩ 0                 , otherwise

cubic B-spline:

       ⎧ 1/2 |x|³ - |x|² + 2/3        , 0 ≤ |x| < 1
B(x) = ⎨ -1/6 |x|³ + |x|² - 2|x| + 4  , 1 ≤ |x| < 2
       ⎩ 0                            , otherwise

基底函數的誤差。此基底函數不符合基底內插的基本要求。粒格來回轉換，物理量損失極大。此基底函數缺乏科學根據，僅是工程經驗。然而目前也沒有更科學的方法了。

一、需要調整參數（彈性係數、重力）以彌補損失。

二、物理量損失，恰巧當作阻尼力，避免柔體振動不止。

基底函數的次方。次方跟誤差無關。次方跟連續有關。次方越高，內插結果越圓融、越做作。

一、當粒子稠密，採用零次方（格內粒子物理量平均數）。當粒子稀疏，採用高次方。質點法刻意讓粒子稀疏，節省時間。質點法採用高次方。

二、格子無所謂稠密稀疏。質點法採用相同次方，節省程式碼。

三、質點法需要用到基底函數的導數。採用二次方以上，基底函數的導數才是連續函數。

物理量的粒格轉換。首先定義位置的粒格轉換，然後推導速度的粒格轉換，然後推導加速度的粒格轉換。其他物理量如法炮製。

（對時間微分：基底函數不含時間，視作常數。）

xᵢ = sum wᵢₚ xₚ     position
vᵢ = sum wᵢₚ vₚ     velocity
aᵢ = sum wᵢₚ aₚ     acceleration

     d       d                      d
vᵢ = —— xᵢ = —— sum wᵢₚ xₚ = sum wᵢₚ —— xₚ = sum wᵢₚ vₚ
     dt      dt                     dt

物理量的梯度的粒格轉換。大家習慣把數學公式刪去一項。我不知道為什麼。我猜測正是因為少了一項，才需要FLIP來彌補損失。

（對空間微分：基底函數包含空間，引用product rule）。

∇qᵢ = sum (∇wᵢₚ ⊗ qₚ) + (wᵢₚ ∇qₚ)   product rule
∇qᵢ = sum ∇wᵢₚ ⊗ qₚ                 don't ask me why

物理量的散度的粒格轉換。也少了一項。

（柔體模擬，只有用到應力的散度。應力恰是對稱矩陣，張量雙點積恰是矩陣乘法。）

∇∙qᵢ = sum (qₚ : ∇wᵢₚ) + (wᵢₚ : ∇qₚ)   product rule
∇∙qᵢ = sum qₚ : ∇wᵢₚ                   don't ask me why

material point method: the prototype

粒的優點：容易紀錄物體形狀。網格是形狀，點是粒，邊是作用力。流體模擬，邊端點隨時改變。柔體模擬，邊端點固定不變。

粒的缺點：無法計算物理量的梯度散度旋度。

格的優點：容易計算物理量的梯度散度旋度。

格的缺點：難以紀錄物體形狀。level set程式碼又臭又長。

兩者優缺點互補，那就聯手合作吧。粒負責形狀，格負責力。

質量與速度，從粒變格，以計算力。

力，從格變粒，以更新速度與位置。

天造地設，可喜可賀。

=======================
粒 particle
=======================

質量　　　mass               mₚ
位置　　　position           xₚ
速度　　　velocity           vₚ

=======================
粒化格 particle to grid
=======================

質量　　　mass               mᵢ = sum wᵢₚ mₚ
速度　　　velocity           vᵢ = sum wᵢₚ vₚ

=======================
格 grid
=======================

速度梯度　velocity gradient  ∇vᵢ = (vᵢ - vᵢ₋₁) / Δx
應變率　　strain rate        ε̇ᵢ = (∇vᵢ + (∇vᵢ)ᵀ) / 2
應變　　　strain             εᵢ = εᵢ + ε̇ᵢ Δt
應力　　　stress             σᵢ = - C : εᵢ
內力　　　internal force     fᵢ = ∇∙σᵢ (Δx)³
外力　　　external force     fᵢ = fᵢ + g

動量　　　momentum           pᵢ = sum mᵢ pᵢ
動量更新　momentum update    pᵢ = pᵢ + fᵢ Δt
速度　　　velocity           vᵢ = pᵢ / mᵢ
加速度　　acceleration       aᵢ = fᵢ / mᵢ

=======================
格化粒 grid to particle
=======================

速度　　　velocity           v̕ₚ = sum wᵢₚ vᵢ
加速度　　acceleration       a̕ₚ = sum wᵢₚ aᵢ

=======================
粒 particle
=======================

位置更新　position update    xₚ = xₚ + v̕ₚ Δt
速度更新　velocity update    vₚ = vₚ + a̕ₚ Δt

material point method: linear elasticity

模擬流程。源自這篇論文：

《Application of a Particle-in-Cell Method to Solid Mechanics》

=======================
粒化格 particle to grid
=======================

動量　　　momentum           pᵢ = sum wᵢₚ pₚ
　　　　　                   where pₚ = mₚ vₚ
內力　　　internal force     fᵢ = sum (∇wᵢₚ : σₚ) (Δx)³
外力　　　external force     fᵢ = fᵢ + g
動量更新　momentum update    pᵢ = pᵢ + fᵢ Δt
加速度　　acceleration       aᵢ = fᵢ / mᵢ
速度　　　velocity           vᵢ = pᵢ / mᵢ

=======================
格化粒 grid to particle
=======================

速度更新　velocity update    vₚ = vₚ + aₚ Δt
　　　　　                   where aₚ = sum wᵢₚ aᵢ
位置更新　position update    xₚ = xₚ + vₚ Δt
　　　　　                   where vₚ = sum wᵢₚ vᵢ
速度梯度　velocity gradient  ∇vₚ = sum ∇wᵢₚ ⊗ vᵢ
應變率　　strain rate        ε̇ₚ = (∇vₚ + (∇vₚ)ᵀ) / 2
應變　　　strain             εₚ = εₚ + ε̇ₚ Δt
應力　　　stress             σₚ = - C : εₚ

雛形版本改良為正式版本：

一、「質量速度粒化格」改成「動量粒化格」。數值更精準。

二、速度梯度「格計算」改成「粒格轉換公式」。不必外插。

三、承上，速度梯度「使用新速度」改成「使用舊速度」。這是錯誤。這是不必外插的代價。魔鬼交易。

四、承上，應變率應變應力「粒化格、格計算」改成「粒計算、粒化格」。根據分配律，計算結果相同。

五。速度梯度應變率應變應力挪到模擬流程末端。速度位置「粒格轉換」「更新」合併式子。最後形成兩大段落，節省程式碼。

接著說明一下正式版本的各種細節。

配置（粒）。均勻擺放。粒多於格。

配置（格）。colocated grid，物理量在格中央。

我的實作當中，加0.5微調位置。我不確定是否合理。

一、粒挪半個間距，避免貼齊物體邊緣。方便繪製寬厚粒子。

二、格挪半格寬度，讓格中央貼齊牆壁。方便指定牆壁速度。

三、多圍一層格子。方便捕捉穿牆粒子。

步幅。順利閃避移位條件，卻無法閃避移位差距條件。

一、移位條件：格子（內的粒子）的移動距離，不可以超過一個格子。否則速度可能高速逸散。數學術語是CFL condition。

二、移位差距條件：相鄰格子（內的粒子）的移動距離的差距，不可以超過一個格子。否則粒化格將漏掉該格。導致物體不再連續。

質點法藉由粒子，順利閃避移位條件，讓Δt變大，讓動畫順暢。計算速度場，不再使用格子。均勻散佈粒子，每個粒子按照速度來運動，求得新位置。粒化格，即得速度場。

儘管質點法順利閃避移位條件，但是深層細節浮上檯面。移位差距條件誕生了。只能面對了。

流體模擬，水流互相推動，速度差異不大，容易滿足移位差距條件。柔體模擬，彈簧合力太大、彈簧振幅太大，難以滿足移位差距條件，導致物體裂開，甚至導致粒子高速逸散。

想要滿足移位差距條件，有四種方式：

一、降低Δt或外力（解析度不變、計算量不變）。

二、增加粒子數量（解析度增加、計算量增加）。

三、增加格子寬度（解析度降低、計算量降低）。

四、改變演算法。流體模擬，可以改變擴散與流動的演算法，讓Δt變大。數學術語是implicit Euler method。柔體模擬，目前沒有演算法。等你發表論文。

繪圖（粒）。mesh rendering。粒子位置，作為點，粒子事先兩兩相連，作為邊。

繪圖（格）。voxel rendering。質量大於零，作為物體。質量的梯度，作為表面法向量。

形變。粒子位置（網格形狀）。

應力。格子表面壓力。採用colocated grid。

colocated grid：應力在格中央。一個格子有兩個應力（共四個分量）。
staggered grid：應力在格表面。一個面有一個應力（兩個分量）。

應力來自形變。考慮下述兩點：

一、彈簧力：

首先求得移位。

形變長度－原本長度＝移位。然而粒的長度不好處理。

速度梯度ｘ時間＝移位。質點法採用其他公式繞過形變。

以移位求得應變。側向移位，功效相同，相加除以二，平均數。物理術語是Saint-Venant's compatibility condition。

以應變求得應力。模仿彈簧，但是不限相同方向，例如X應變可以得到Y應力。一個應變有四個彈性係數暨彈簧力。四個應變就是十六個。相同方位的彈簧力，加總，形成四個應力分量。物理術語是linear elasticity。

二、表面形狀：

形變改變格子形狀，改變表面積與表面法向量，改變應力大小與應力方向。物理術語是Cauchy stress或true stress。

質點法重新劃分格子，運用粒格轉換求得新應力。物理術語是first Piola–Kirchhoff stress或nominal stress。

大家只做彈簧力、沒做表面形狀。等你發表論文。

material point method: hyperelasticity

模擬流程。源自這篇論文：

《A Material Point Method for Snow Simulation》

然而這是Disney的專利。冰雪奇緣Frozen。

=======================
粒化格 particle to grid
=======================

動量　　　momentum               pᵢ = sum wᵢₚ pₚ
　　　　　                       where pₚ = mₚ vₚ
動量守恆　momentum conservation  FLIP/APIC
內力　　　internal force         fᵢ = sum (∇wᵢₚ : σ̅ₚ) (Δx)³
外力　　　external force         fᵢ = fᵢ + g
動量更新　momentum update        pᵢ = pᵢ + fᵢ Δt
加速度　　acceleration           aᵢ = fᵢ / mᵢ
速度　　　velocity               vᵢ = pᵢ / mᵢ

=======================
格化粒 grid to particle
=======================

位置更新　position update        xₚ = xₚ + vₚ Δt
　　　　　                       where vₚ = sum wᵢₚ vᵢ
速度更新　velocity update        vₚ = sum wᵢₚ vᵢ
速度梯度　velocity gradient      ∇vₚ = sum ∇wᵢₚ ⊗ vᵢ
形變梯度　deformation gradient   Fₚ = Fₚ + ∇vₚ Δt
能量密度　strain energy density  Ψₚ = μ‖Fₚ-Rₚ‖² + ½λ‖Jₚ-1‖²
中繼項　　force-based stress     σ̅ₚ = - ∂Ψₚ/∂Fₚ Fₚᵀ

這個版本將彈性模型「線性彈性」改成「超彈性」。超彈性支援更多種類的物體，例如雪、沙、果膠、牙膏、醬汁、蛋糕、……。只需調整能量密度Ψ、彈性係數μ和λ。

線性彈性以應變應力求得力。超彈性以能量密度Ψ、形變梯度F求得力。

f = ∂Φ/∂x             能量對位置微分，得到力。f = ∂Φ/∂x。
f = ∫ ∂Ψ/∂x dV        能量對體積微分，得到能量密度。Ψ = ∂Φ/∂V。
f = ∫ ∂Ψ/∂F ∂F/∂x dV  微積分chain rule，強行湊出形變梯度F。

依據上述公式，使用質點法求得力。

一、Ψ：自行定義數學式子，根據柔體類型。

二、∂Ψ/∂F：手工推導數學式子，藉由矩陣函數微積分。

三、∂F/∂x：繞過去。運用粒格轉換，化作基底函數的梯度。

四、dV：格體積。

fᵢ = sum Vₚ ∂Ψₚ/∂Fₚ ∂Fₚ/∂xₚ wᵢₚ     粒格轉換
fᵢ = sum Vₚ ∂Ψₚ/∂Fₚ Fₚᵀ ∇wᵢₚ        化作基底函數的梯度
            ^^^^^^^^^
                σ̅ₚ                 中繼項（類似於應力平均數）

Vₚ       = (Δx)³                           格體積
Ψₚ       = μ ‖Fₚ - Rₚ‖² + ½λ ‖Jₚ - 1‖²      自行定義
∂Ψₚ/∂Fₚ  = 2μ (Fₚ - Rₚ) + λ (Jₚ - 1) Jₚ Fₚ⁻ᵀ 手工推導

{Rₚ, Sₚ} = polar(Fₚ)                        極分解
Jₚ       = det(Fₚ)                          行列式
{μ, λ}   = constants                       彈性係數

更新。形變梯度更新公式源自dF/dt = ∇v。論文作者看似引用dF/dt = LF，我認為引用錯誤，在這裡特地提出來。

[correct formula]
Fₚ = Fₚ + ∇vₚ Δt                 dF/dt = ∇v
where ∇vₚ = sum vᵢ ∇wᵢₚᵀ

[Stomakhin et al. 2013]
Fₚ = ( I + ∇vₚ Δt ) Fₚ           dF/dt = LF
where ∇vₚ = sum vᵢ ∇wᵢₚᵀ

[Jiang–Gast–Teran 2017]
Fₚ = ∇xₚ Fₚ                      don't ask me why
where ∇xₚ = sum xᵢ ∇wᵢₚᵀ        just free your mind

步幅。等你發表論文。實測結果是Δt必須變得更小。

此方式容易裂開，雪也容易裂開，真巧。就算調參失敗、模擬失真，外表也看不出來，真巧。

守恆。校正速度場，令物理量守恆。兩種方法FLIP和APIC。

一、FLIP：原數值和相差值的加權平均數。PD controller。

《FLIP: A Method for Adaptively Zoned, Particle-in-Cell Calculuations of Fluid Flows in Two Dimensions》

二、APIC：額外補上相差值的渦度。我還沒有看懂。

《The Affine Particle In Cell Method》

APIC源自Disney的專利。按理來說，大家不得使用。不過最近Blender和Houdini實作了APIC。也許大家達成了共識。

[FLIP]
vₚ = (1 - α) vₚPIC + α vₚFLIP
where vₚPIC = sum vᵢ wᵢₚᵀ
where vₚFLIP = vₚold + sum (vᵢ - vᵢold) wᵢₚᵀ
where α = 0.95

[APIC]
mᵢ vᵢ = sum wᵢₚ mₚ vₚ
      + sum wᵢₚ mₚ Bₚ Dₚ⁻¹ (xᵢ - xₚ)
where Dₚ = wᵢₚ (xᵢ - xₚ) (xᵢ - xₚ)ᵀ
where Bₚ = wᵢₚ vᵢ (xᵢ - xₚ)ᵀ

碰撞。多個柔體互相接觸。細分為恢復和摩擦。

一、恢復：不同柔體的粒子，設定為不同質量。依照原本模擬流程，無須額外數學公式。

二、摩擦：我沒有研究。詳情請見下述論文。

《A Hybrid Material Point Method for Frictional Contact with Diverse Materials》

接觸。對柔體施力。接觸位置追加外力。

一、所在格子追加外力：物理術語是Kelvin state，有公式解。

二、周遭格子追加外力：常態分布，中心強外圍弱。論文作者稱作Kelvinlet。

三、同時配合Poisson's ratio，調整形狀扭曲程度。

《Regularized Kelvinlets: Sculpting Brushes based on Fundamental Solutions of Elasticity》

然而這是Pixar的專利。海底總動員第二集Finding Dory。

soft body

剛體。形狀固定不變，無論如何運動。

柔體。形狀可以改變。

soft body motion

數學幾何變換有三個因素：平移、旋轉、縮放。

物質運動區分為三個項目：質點、剛體、柔體。

質點：平移。
剛體：平移、旋轉。
柔體：平移、旋轉、縮放。

柔體運動區分為許多項目。

motion 丨中文丨意義
-------丨一一丨一一一一一一一一一一
move   丨移動丨平移：平面一齊移動
skew   丨歪斜丨平移：平面切向量方向
bend   丨彎曲丨旋轉：平面切向量為軸
twist  丨扭轉丨旋轉：平面法向量為軸
stretch丨拉伸丨縮放：平面法向量方向

soft body force

運動方式的差異，源自於施力方式的差異。

phenomenon  | force             丨中文　丨意義
------------| ------------------丨一一一丨一一一一一一一一一一
            | normal force      丨正向力丨正向力，表面垂直方向
            | shear force       丨剪力　丨側向力，表面水平方向
------------| ------------------丨一一一丨一一一一一一一一一一
tension     | tensile force     丨張力　丨兩力方向相反，朝外
compression | compressive force 丨壓縮力丨兩力方向相反，朝內

elasticity / plasticity / fracture

柔體形狀變化分為三個階段，根據變化程度。

term        丨中文丨意義
------------丨一一丨一一一一一一一一一一一一一一一一一一一
elasticity  丨彈性丨形狀變化輕微／施力輕微，將會恢復形狀。
plasticity  丨塑性丨形狀變化較多／施力較多，不會恢復形狀。
fracture    丨破裂丨形狀變化太多／施力太多，形狀破裂分離。

產生塑性的時候，通常保有部分彈性。產生破裂的時候，通常也保有部分彈性。例如紅豆麻糬。

以下只介紹彈性。至於塑性和破裂，大家仍在研究如何模擬，無法整理成篇。等你發表論文。

elastic model

想要描述彈性，主要有三種方式：實驗數據、線性、非線性。

term               丨中文　　　　丨意義
-------------------丨一一一一一一丨一一一一一一一一一一一一一一一
stress-strain curve丨應力應變曲線丨應變套用實驗數據得到應力。
linear elasticity  丨線性彈性　　丨應變套用線性函數得到應力。
hyperelasticity    丨超彈性　　　丨自訂能量。對形變微分得到應力。

實驗數據是最準確的方式，但是目前沒人採用此方式。我在這裡特地提出來，也許大家會開始重視實驗數據。隔壁棚illumination model從Phong shading過渡到BRDF，最終也是採用實驗數據。

後面兩章分別介紹線性彈性、超彈性。

linear elasticity

引用彈簧運動來描述柔體運動。一維彈簧推廣成三維柔體，形成許多步驟，流程如下：

   deformation            x
-> deformation gradient   F = ∇x
-> displacement gradient  ∇u = F - I
-> strain                 ε = (∇u + (∇u)ᵀ) / 2
-> stress                 σ = - C : ε
-> velocity               ⎰ ∂ρ/∂t + ∇∙(ρv) = 0
                          ⎱ ∂(ρv)/∂t + ∇∙(ρv⊗v) + ∇∙σ = 0

柔體模擬，需要位置和速度。設定當前時刻的deformation。套用上述流程得到當前時刻的速度。套用下述任意一道數學公式，得到下個時刻的物理量。套用上述流程得到下個時刻的速度。

1. deformation gradient rate  ∂F/∂t = ∇v
2. displacement rate          ∂(∇u)/∂t = ∇v
3. strain rate                ∂ε/∂t = (∇v + (∇v)ᵀ) / 2

prologue: deformation comes from joint motion

剛體運動和柔體運動採用了完全不同的策略。

剛體運動：細分為移動和轉動，形成兩套相似的物理量。

柔體運動：一律視作移動，只有一套物理量。

物體視作質點相連。運動視作質點運動。

旋轉運動：垂直於質點連接方向。

縮放運動：水平於質點連接方向。

旋轉運動、縮放運動，通通視作平移運動。

物理學沒有「縮放運動」這個詞彙。我們懷念他。

prologue: strain and stress come from spring

模仿了彈簧虎克定律。基本單位改成比率，於是另起名稱。

displacement     Δx        <-> strain                ε
Hooke's constant k         <-> Young's modulus       E
force            F = kΔx   <-> stress                σ = Eε
potential energy U = ½kΔx² <-> strain energy density Ψ = ½Eε²

length                x
displacement          Δx
strain                ε = Δx/x (displacement per length)

area                  A
force                 F
stress                σ = F/A  (force per area)

volume                V
potential energy      U
strain energy density Ψ = U/V  (potential energy per volume)

term        丨中文　丨原意丨定義
------------丨一一一丨一一丨一一一一一一一一一一一一一一一
strain      丨應變　丨繃緊丨物體邊長，每單位長度的長度差異
stress      丨應力　丨著重丨物體表面，每單位面積的力

基本單位改成比率，背後原因是微積分。物理學家喜歡用微積分來描述物理現象，而微分運算結果就是比率。

deformation

進入正題，開始介紹三維柔體。

三維物體形狀改變，利用數學的幾何變換來描述。

⎡x'⎤     ⎡x⎤ 
⎢y'⎥ = f(⎢y⎥)   or  x' = f(x)
⎣z'⎦     ⎣z⎦ 

物理學家令原座標是大寫字母，新座標是小寫字母。

⎡x⎤     ⎡X⎤ 
⎢y⎥ = f(⎢Y⎥)   or  x = f(X)
⎣z⎦     ⎣Z⎦ 

物理學家習慣用函數輸出符號x代替函數符號f。只需要注意x和X，不需要注意f。x的本質是函數，計算要特別小心。

f(X) ---> x(X)

物理學家習慣省略函數括號。本質仍是函數，計算要特別小心。

x(X) ---> x

deformation gradient

     ∂x
∇x = ——
     ∂X

     ⎡ ∂x ∂y ∂z ⎤
     ⎢ —— —— —— ⎥
     ⎢ ∂X ∂X ∂X ⎥
     ⎢          ⎥
     ⎢ ∂x ∂y ∂z ⎥
∇x = ⎢ —— —— —— ⎥ 
     ⎢ ∂Y ∂Y ∂Y ⎥
     ⎢          ⎥
     ⎢ ∂x ∂y ∂z ⎥
     ⎢ —— —— —— ⎥
     ⎣ ∂Z ∂Z ∂Z ⎦

流行的梯度定義：同一變數對不同變數微分是矩陣橫條。
本站的梯度定義：同一變數對不同變數微分是矩陣直條。

新長度∂x和原長度∂X的比率。x和X是數量，除法得到比率。x和X是函數，微分得到比率。

9個數值。物體切割成微小立方體，微小立方體有三個軸（分母），每個軸又有三個移動方向（分子）。

    ∂x
F = ——
    ∂X

物理學家習慣將deformation gradient重新標記成大寫F。以下只好把force重新標記成小寫f。

displacement

u = x - X

    ⎡ x - X ⎤
u = ⎢ y - Y ⎥
    ⎣ z - Z ⎦

新位置x與原位置X的差異。

3個數值。物體有三個軸，每個軸各有一個偏移量。

displacement gradient

     ∂u   ∂(x-X)
∇u = —— = ——————
     ∂X     ∂X

     ⎡ ∂(x-X) ∂(y-Y) ∂(z-Z) ⎤   ⎡ ∂(x-X)   ∂y     ∂z   ⎤
     ⎢ —————— —————— —————— ⎥   ⎢ ——————   ——     ——   ⎥
     ⎢   ∂X     ∂X     ∂X   ⎥   ⎢   ∂X     ∂X     ∂X   ⎥
     ⎢                      ⎥   ⎢                      ⎥
     ⎢ ∂(x-X) ∂(y-Y) ∂(z-Z) ⎥   ⎢   ∂x   ∂(y-Y)   ∂z   ⎥
∇u = ⎢ —————— —————— —————— ⎥ = ⎢   ——   ——————   ——   ⎥
     ⎢   ∂Y     ∂Y     ∂Y   ⎥   ⎢   ∂Y     ∂Y     ∂Y   ⎥
     ⎢                      ⎥   ⎢                      ⎥
     ⎢ ∂(x-X) ∂(y-Y) ∂(z-Z) ⎥   ⎢   ∂x     ∂y   ∂(z-Z) ⎥
     ⎢ —————— —————— —————— ⎥   ⎢   ——     ——   —————— ⎥
     ⎣   ∂Z     ∂Z     ∂Z   ⎦   ⎣   ∂Z     ∂Z     ∂Z   ⎦

新舊長度差異∂x-∂X與原長度∂X的比率。

9個數值。3個正向，6個側向。物理術語是normal displacement gradient和shear displacement gradient。

∇u = F - I

物理學家習慣用deformation gradient直接求得displacement gradient。正向扣掉原長度（比率1），側向不必扣掉原長度（側向的原長度是0）。恰是線性代數的恆等矩陣I。

strain

ε = (∇u + (∇u)ᵀ) / 2

    ⎡     ∂(x-X)     1 ⎛ ∂x   ∂y ⎞  1 ⎛ ∂x   ∂z ⎞ ⎤
    ⎢     ——————     — ⎜ —— + —— ⎟  — ⎜ —— + —— ⎟ ⎥
    ⎢       ∂X       2 ⎝ ∂Y   ∂X ⎠  2 ⎝ ∂Z   ∂X ⎠ ⎥
    ⎢                                             ⎥
    ⎢ 1 ⎛ ∂x   ∂y ⎞      ∂(y-Y)     1 ⎛ ∂y   ∂z ⎞ ⎥
ε = ⎢ — ⎜ —— + —— ⎟      ——————     — ⎜ —— + —— ⎟ ⎥
    ⎢ 2 ⎝ ∂Y   ∂X ⎠        ∂Y       2 ⎝ ∂Z   ∂Y ⎠ ⎥
    ⎢                                             ⎥
    ⎢ 1 ⎛ ∂x   ∂z ⎞  1 ⎛ ∂y   ∂z ⎞      ∂(z-Z)    ⎥
    ⎢ — ⎜ —— + —— ⎟  — ⎜ —— + —— ⎟      ——————    ⎥
    ⎣ 2 ⎝ ∂Z   ∂X ⎠  2 ⎝ ∂Z   ∂Y ⎠        ∂Z      ⎦

    ⎡ εₓₓ ε₝ₓ ε₞ₓ ⎤
ε = ⎢ εₓ₝ ε₝₝ ε₞₝ ⎥   where εₓ₝ = ε₝ₓ, εₓ₞ = ε₞ₓ, ε₝₞ = ε₞₝
    ⎣ εₓ₞ ε₝₞ ε₞₞ ⎦

本來，strain即是displacement gradient。

9個數值。3個正向，6個側向。物理術語是normal strain和shear strain。

後來，物理學家嘗試各種改造方式，以便得到各種彈性模型。strain是經過改造的displacement gradient。

其中一種改造方式：成對的shear strain，視作功效相同。數值重新設定成兩者平均數，使得數值相同。物理術語是Saint-Venant's compatibility condition。

仍是9個數值，但是只有6種數值。3種扯面、3種扯邊。

stress

    ⎡ σₓₓ σ₝ₓ σ₞ₓ ⎤
σ = ⎢ σₓ₝ σ₝₝ σ₞₝ ⎥   where σₓ₝ = σ₝ₓ, σₓ₞ = σ₞ₓ, σ₝₞ = σ₞₝
    ⎣ σₓ₞ σ₝₞ σ₞₞ ⎦

物體切割成微小立方體。一個立方體有六個面。一個面有一個力。力除以表面積，形成壓力（向量）。一個壓力有3個分量。1個正向、2個側向。

一個立方體有6個壓力。兩個立方體的接觸面的壓力是相等的（方向相反）。一個立方體負責記錄3個壓力（colocated grid）。

9個數值。3個正向、6個側向。物理術語是normal stress和shear stress。

沿用先前的改造方式：成對的shear stress，數值相同。

仍是9個數值，但是只有6種數值。3種正向、3種側向。

linear elasticity與elastic modulus

σ = C : ε

ε is Cauchy strain tensor (order-2) (3x3)
σ is Cauchy stress tensor (order-2) (3x3)
C is elastic modulus tensor (order-4) (3x3x3x3)
: is double dot product

線性：模仿彈簧，但是不限相同方向。例如X軸strain可以得到Y軸stress。

9個strain，使用81個彈性係數，得到81個stress。相同方位的stress進行加總，最後得到9個stress。

物理學家寫成張量雙點積。計算學家寫成矩陣乘法。

tensor double dot product
⎡ σₓₓ σ₝ₓ σ₞ₓ ⎤   ⎡       ⎤   ⎡ εₓₓ ε₝ₓ ε₞ₓ ⎤
⎢ σₓ₝ σ₝₝ σ₞₝ ⎥ = ⎢   C   ⎥ : ⎢ εₓ₝ ε₝₝ ε₞₝ ⎥
⎣ σₓ₞ σ₝₞ σ₞₞ ⎦   ⎣       ⎦   ⎣ εₓ₞ ε₝₞ ε₞₞ ⎦
      ₃ₓ₃          ₃ₓ₃ₓ₃ₓ₃          ₃ₓ₃

matrix product
⎡ σₓₓ ⎤   ⎡ Cₓₓₓₓ Cₓₓₓ₝ ... ... ⎤ ⎡ εₓₓ ⎤
⎢ σₓ₝ ⎥   ⎢ Cₓ₝ₓₓ Cₓ₝ₓ₝ ... ... ⎥ ⎢ εₓ₝ ⎥
⎢ σₓ₞ ⎥   ⎢ Cₓ₞ₓₓ Cₓ₞ₓ₝ ... ... ⎥ ⎢ εₓ₞ ⎥
⎢ σ₝ₓ ⎥   ⎢ C₝ₓₓₓ C₝ₓₓ₝ ... ... ⎥ ⎢ ε₝ₓ ⎥
⎢ σ₝₝ ⎥ = ⎢ C₝₝ₓₓ C₝₝ₓ₝ ... ... ⎥ ⎢ ε₝₝ ⎥
⎢ σ₝₞ ⎥   ⎢ C₝₞ₓₓ C₝₞ₓ₝ ... ... ⎥ ⎢ ε₝₞ ⎥
⎢ σ₞ₓ ⎥   ⎢ C₞ₓₓₓ C₞ₓₓ₝ ... ... ⎥ ⎢ ε₞ₓ ⎥
⎢ σ₞₝ ⎥   ⎢ C₞₝ₓₓ C₞₝ₓ₝ ... ... ⎥ ⎢ ε₞₝ ⎥
⎣ σ₞₞ ⎦   ⎣ C₞₞ₓₓ C₞₞ₓ₝ ... ... ⎦ ⎣ ε₞₞ ⎦
  ₉ₓ₁                ₉ₓ₉            ₉ₓ₁

沿用先前的改造方式：只有36種彈性係數。

6種strain、36種彈性係數、6種stress的矩陣乘法。索引值重新安排，3種正向、3種側向。物理術語是Voigt notation。

Voigt notation
⎡ σₓₓ ⎤   ⎡ Cₓₓₓₓ Cₓₓ₝₝ ... ... ⎤ ⎡ εₓₓ ⎤
⎢ σ₝₝ ⎥   ⎢ C₝₝ₓₓ C₝₝₝₝ ... ... ⎥ ⎢ ε₝₝ ⎥
⎢ σ₞₞ ⎥ = ⎢ C₞₞ₓₓ C₞₞₝₝ ... ... ⎥ ⎢ ε₞₞ ⎥
⎢ σₓ₝ ⎥   ⎢ Cₓ₝ₓₓ Cₓ₝₝₝ ... ... ⎥ ⎢ εₓ₝ ⎥
⎢ σₓ₞ ⎥   ⎢ Cₓ₞ₓₓ Cₓ₞₝₝ ... ... ⎥ ⎢ εₓ₞ ⎥
⎣ σ₝₞ ⎦   ⎣ C₝₞ₓₓ C₝₞₝₝ ... ... ⎦ ⎣ ε₝₞ ⎦
  ₆ₓ₁                ₆ₓ₆            ₆ₓ₁

isotropic linear elasticity與Lamé's parameters

σ = λ tr(ε) I + 2με

⎧ σₓₓ = λ(εₓₓ + ε₝₝ + ε₞₞) + 2μ εₓₓ
⎪ σ₝₝ = λ(εₓₓ + ε₝₝ + ε₞₞) + 2μ ε₝₝
⎨ σ₞₞ = λ(εₓₓ + ε₝₝ + ε₞₞) + 2μ ε₞₞
⎪ σₓ₝ = σ₝ₓ = 2μ εₓ₝
⎪ σₓ₞ = σ₞ₓ = 2μ εₓ₞
⎩ σ₝₞ = σ₞₝ = 2μ ε₝₞

λ is something like bulk modulus.
μ is both normal modulus and shear modulus.

均向性：抱歉，我不知道這究竟是什麼。

此處的均向性，獨樹一格。它不是isotropic tensor、也不是isotropic transform、更不是rotational invariance。

上述數學式子，許多物理書籍均有提及，但是我無法理解前因後果。我把它當作輕小說設定。古人幻想出來的數學公式。詳情請見專著《Linear and Nonlinear Structural Mechanics》。

又線性又均向性又改造的情況下，根據輕小說設定，只需紀錄兩個彈性係數。物理術語是Lamé's parameters。

Poisson's ratio

ν = - εₓ / ε₞

2個normal strain的比例。肉眼可見，相當直覺。

一般來說，一個維度被擠壓，其他維度會拉伸。因此加上負號。

isotropic linear elasticity與Poisson's ratio

λ = Eν / (1+ν)(1-2ν)
μ = E / 2(1+ν)

又線性又均向性又指定strain比例又改造的情況下，根據輕小說設定，只需紀錄一個彈性係數。姑且稱作Young's modulus。

大家習慣自訂Young's modulus和Poisson's ratio，間接求得Lamé's parameters。

Navier–Cauchy equation

流體方程組＋線性彈性＝柔體方程組。

流體方程組其中一項是應力。藉由流體方程組，以應力求速度。應力有許多種設定方式。先前是應力與應變率成正比（牛頓流體）。此處是應力與應變呈線性關係（線性彈性）。

我習慣讓應力σ添加負號，形成恢復力。

大家習慣省略壓力p，納入應力。

⎧ ∂ρ/∂t + ∇∙(ρv) = 0             conservation of mass
⎨ ∂(ρv)/∂t + ∇∙(ρv⊗v) + ∇∙σ = 0  conservation of momentum
⎪ ∂ε/∂t = (∇v + (∇v)ᵀ) / 2       strain rate
⎩ σ = - C : ε                    linear elasticity

有人追加不可壓縮，表示成物質導數。

某些流體不可壓縮。柔體肯定可以壓縮，不適合這樣做。

⎧ Dρ/Dt = 0
⎨ D(ρv)/Dt + ∇∙σ = 0
⎪ ∂ε/∂t = (∇v + (∇v)ᵀ) / 2
⎩ σ = - C : ε

有人追加均向性，表示成Lamé's parameters。

推導過程請見維基百科。

⎰ Dρ/Dt = 0
⎱ D(ρv)/Dt - (λ+μ) ∇∇∙u​​ - μ ∇∙∇u = 0

σ = -(λ tr(ε) I + 2με)
∇∙σ = -((λ+μ)∇∇∙u + μ∇∙∇u)

延伸閱讀：σ is wrong!

物理學家認為應變與應力同向。σ = C : ε。

我認為在流體方程組當中必須反向。σ = - C : ε。

換句話說，我認為流體方程組的σ是恢復力。

我將解釋理由。

一、虎克定律。

fₑₓₜ = k Δx
fᵢₙₜ = -k Δx

彈簧力有兩種定義。視情況帶負號。

形變力（外力）：施力導致移位。移位與力同向。

恢復力（內力）：移位導致反彈。移位與力反向。

二、作用力與反作用力定律（動量守恆）。

fᵢₙₜ  + fₑₓₜ = 0
-fᵢₙₜ = fₑₓₜ
k Δx  = fₑₓₜ

動量守恆，內力外力相加等於零。

讓等號左側是運動量，讓等號右側是外力，那麼等號左側帶正號。

三、功能定理。

W = ΔK = fΔx = maΔx = ½mΔ(v²)   ---> K = ½mv²
W = ΔU = fΔx = mgΔx             ---> U = mgh

力ｘ移位＝功。功是能量差異。

四、力學能守恆定律（能量守恆）。

K    + U   = Eₜₒₜₐₗ
½mv² + mgh = Eₜₒₜₐₗ

能量守恆，動能位能相加等於某個常數。

讓等號左側是動能位能，讓等號右側是總和，那麼等號左側帶正號。

五、連續方程式。

朝外為正：物理量增加為正值。物理量朝外流動為正值。形成相加。
朝內為正：物理量增加為正值。物理量朝內流動為正值。形成相減。
　　　　　進一步移項，形成相等。

∂(ρv)/∂t + ∇∙(ρv⊗v) = 0

^^^^^^^^   ^^^^^^^^  
temporal   spatial     
change     change

連續方程式有兩種定義。大家採用「朝外為正值」。

為何採用朝外呢？難道不能朝內嗎？背後原因是微積分。使用微積分描述流動守恆，於是迎合微積分的規矩。如此而已。

散度：朝外為正值。
梯度：右大於左為正值。

另一方面，採用「朝外為正值」，數學式子形成相加，恰好符合能量守恆的格式。完美詮釋「流動守恆，總和為定值」。

六、流體方程組。

∂(ρv)/∂t + ∇∙(ρv⊗v) + ρg     + ∇p     + ∇∙σ    = 0

^^^^^^^^   ^^^^^^^^   ^^^^^^^  ^^^^^^^  ^^^^^^^
temporal   spatial    order-1  order-0  order-2
change     change     tensor   tensor   tensor

^^^^^^^^^^^^^^^^^^^   ^^^^^^^^^^^^^^^^^^^^^^^^^
kinetic               potential
force density         force density

追加三項，重力密度ρg、壓力p、應力σ。我認為它們宛如位能。我認為等號左側應該帶正號。

p考慮正向。σ考慮正向和側向。線性彈性當中，p是σ的特例，兩者可以整併，只留下σ。

七、牛頓流體。

σ       = - ν            (∂ε/∂t)

^^^^^^^     ^^^^^^^^^^^  ^^^^^^^^^^^
stress      viscosity    strain rate

^^^^^^^     ^^^^^^^^^^^  ^^^^^^^^^^^
damping     damping      velocity
            coefficient

應變率視作速度，整個式子其實就是阻尼！

阻尼減緩速度。阻尼與速度反向，總是帶負號。

讓應變與應力反向，牛頓流體自然而然帶負號，牛頓流體自然而然是阻尼。阻尼＝黏滯。完美詮釋「該係數是負面詞彙黏滯係數，而不是正面詞彙流暢係數」。

∂(ρv)/∂t + ∇∙(ρv⊗v) + ρg + ∇p - ν ∇∙∇v = 0
                                ^^^^^^
                                damping

擴散帶負號，也就是阻止擴散。

八、線性彈性。

σ      = - C               : ε

^^^^^^     ^^^^^^^^^^^^^^^   ^^^^^^
stress     elastic modulus   strain

應變視作移位，整個式子其實就是彈簧的恢復力（的密度）！

∂(ρv)/∂t + ∇∙(ρv⊗v) + ρg + ∇p - ∇∙(C:ε)  = 0
                                ^^^^^^^     
                                restoring force density

彈簧力帶負號，也就是恢復力（的密度）。

九、心得感想。

我認為流體方程組、柔體方程組當中，應變與應力反向。

如此一來，流體方程組、柔體方程組，更容易理解。

我希望往後的物理教科書也能採用這種方式。

σ是恢復力。這樣才是正港的彈性！

rate of physical quantities

物理量對時間微分，整理成速度梯度。數學公式推導過程如下。

1. deformation gradient rate ∂F/∂t = ∇v

  ∂F/∂t
= ∂/∂t F                      operator notation
= ∂/∂t (∂/∂X u + I)           ∇u = F - I
= ∂/∂t ∂/∂X u + ∂/∂t I        distributive law
= ∂/∂t ∂/∂X u                 derivative of constant is 0
= ∂/∂X ∂/∂t u                 commutative law
= ∂/∂X v                      v = ∂u/∂t
= ∂v/∂X                       fraction notation

2. displacement rate ∂(∇u)/∂t = ∇v

u = x - X                     by definition
∂/∂t u = v                    by definition
∂/∂X ∂/∂t u = ∂/∂X v          apply ∂/∂X to both sides
∂/∂t ∂/∂X u = ∂/∂X v          commutative law

3. strain rate ∂ε/∂t = (∇v + (∇v)ᵀ)/2

ε = (∇u + (∇u)ᵀ)/2            by definition
∂/∂t ε = ∂/∂t (∇u + (∇u)ᵀ)/2  apply ∂/∂t to both sides
∂/∂t ε = (∇v + (∇v)ᵀ)/2       commutative law

有人修改速度梯度的定義，數學公式變得不太一樣。

1. deformation gradient rate ∂F/∂t = L F

∇v = dv/dX                     initial coordinates X
L = dv/dx                      current coordinates x

  ∂F/∂t
= ∂v/∂X                        ∂F/∂t = ∇v
= ∂v/∂x ∂x/∂X                  chain rule
= L F

hyperelasticity

用形變與能量來描述柔體運動，流程如下：

   deformation gradient    F
-> Green strain            Ε = (FᵀF - I) / 2
-> strain energy density   Ψ = ½ λ tr(Ε)² + μ tr(Ε²)
-> Piola–Kirchhoff stress  P = ∂Ψ/∂F   ✘
-> Cauchy stress           σ = -PFᵀ/det(F)
-> velocity                ⎰ ∂ρ/∂t + ∇∙(ρv) = 0
                           ⎱ ∂(ρv)/∂t + ∇∙(ρv⊗v) + ∇∙σ = 0

流體模擬，需要銜接此步驟，得到下個時刻的物理量：

-> deformation gradient rate  ∂F/∂t = ∇v

prologue: new relationship

彈簧、線性、均向性，以此得到的數學公式，只能符合真實世界的少數柔體。物理學家的說詞：只適合小幅形變，不適合大幅形變。

既有的數學公式無法投入實用，物理學家重新發明數學公式，形成新流派，稱作「hyperelasticity超☆彈性」。

這些數學公式，完全憑感覺，一個比一個唬爛，連一個數學性質都不必證明。但是我們也沒有更好的方法了。面對亂七八糟的形變，只好用亂七八糟的算法。

最佳化的「metaheuristics超☆啟發」也是類似的新流派。既有的最佳化演算法無法投入實用，大家重新發明基因演算法、蟻群演算法、粒子群演算法，諸如此類的。

prologue: relationship of force and potential energy

strain energy density對strain微分得到stress。

potential energy U = ½kΔx² <-> strain energy density Ψ = ½Eε²
force            f = ∂U/∂x <-> stress                σ = ∂Ψ/∂ε

超彈性的大意：

一、重新發明strain energy density。

二、對其他物理量微分，例如deformation。

三、想辦法將微分結果變成stress。

deformation gradient

進入正題，假設柔體運動是平移旋轉縮放。

一、平移與旋轉：當作剛體運動，改變物體方位。

二、縮放：當作柔體運動，改變物體形狀。

deformation是平移旋轉縮放。

deformation gradient只剩下旋轉縮放。

一、函數視作多項式，函數微分可以刪除常數項。

二、函數視作幾何變換，函數梯度可以刪除平移變換。

deformation gradient恰是變換矩陣。

deformation gradient拆成旋轉矩陣、拉伸矩陣。兩種方式。

一、奇偶分解＝奇部（旋轉）＋偶部（拉伸）。

二、極分解＝正規正交矩陣（旋轉）ｘ對稱正定矩陣（拉伸）。

F = (F-Fᵀ)/2 + (F+Fᵀ)/2 = R + S   even-odd decomposition
F = UΣVᵀ = (UVᵀ)(VΣVᵀ) = RS       polar decomposition

R   rotation matrix
S   stretch matrix (it is not scaling matrix)

拉伸矩陣拆成縮放方向、縮放比率。利用特徵分解。

一、特徵向量：縮放方向。互相垂直。

二、特徵值：縮放比率。都是正數，如果沒有鏡射。

拉伸矩陣的特徵分解等於奇異值分解。

一、對稱矩陣，存在特徵向量，特徵向量互相垂直。

二、deformation不含鏡射，特徵值都是正數。

拉伸矩陣調整成normal displacement gradient。

一、特徵值減一，即是normal displacement gradient。

二、拉伸矩陣減去恆等矩陣I，則是一口氣將所有特徵值減一，數學術語是eigenvalue shift。

S = EΛE⁻¹                         eigendecomposition
S-I = E(Λ-I)E⁻¹                   eigenvalue shift

先前提到的改造方式Saint-Venant's compatibility condition，其實就是奇偶分解。超彈性則習慣使用極分解。

strain energy density

81種彈簧能量密度總和。9種strain，兩兩相乘。

Ψ = ½ ε:C:ε              (quadratic form)
Ψ = sum ½ Cᵢⱼₖₗ εᵢⱼ εₖₗ
    ⁱʲᵏˡ

strain energy density可以改寫成特徵值。但是只有normal strain，沒有shear strain。特徵值減一當作normal strain。

9種彈簧能量密度總和。3種normal strain，兩兩相乘。

Ψ = ½ C₁₁ (λ₁-1)² + ½ C₂₂ (λ₂-1)² + ½ C₃₃ (λ₃-1)²
  + C₁₂ (λ₁-1)(λ₂-1) + C₁₃ (λ₁-1)(λ₃-1) + C₂₃ (λ₂-1)(λ₃-1)

進一步製造特別的strain：長度、面積、體積。以此製造特別的strain energy density。

line strains:  {λ₁-1 , λ₂-1 , λ₃-1}
plane strains: {λ₁λ₂-1 , λ₁λ₃-1 , λ₂λ₃-1}
bulk strain:   λ₁λ₂λ₃-1

Ψ = ½ C₁₁ (λ₁-1)² + ½ C₂₂ (λ₂-1)² + ½ C₃₃ (λ₃-1)²
  + C₁₂ (λ₁-1)(λ₂-1) + C₁₃ (λ₁-1)(λ₃-1) + C₂₃ (λ₂-1)(λ₃-1)
  + ½ C₁₂₁₂ (λ₁λ₂-1)² + ½ C₁₃₁₃ (λ₁λ₃-1)² + ½ C₂₃₂₃ (λ₂λ₃-1)²
  + C₁₂₁₃ (λ₁λ₂-1)(λ₁λ₃-1) + C₁₂₂₃ (λ₁λ₂-1)(λ₂λ₃-1)
  + C₁₃₂₃ (λ₁λ₃-1)(λ₂λ₃-1)
  + ½ C₁₂₃₁₂₃ (λ₁λ₂λ₃-1)²

太冗長。讓人看了受不了。必須簡化。

isotropic strain energy density

均向性：物體實施旋轉變換，strain energy density仍相同。即是數學術語rotational invariance。

詳情請見專著《Non-Linear Elastic Deformations》。書上稱之為second order isotropic tensor function。

換句話說：特徵值隨意對調，strain energy density仍相同。

換句話說：平方項的彈性係數相同，交叉項的彈性係數相同。

Ψ = ½ C₁ ((λ₁-1)² + (λ₂-1)² + (λ₃-1)²)
  +   C₂ ((λ₁-1)(λ₂-1) + (λ₁-1)(λ₃-1) + (λ₂-1)(λ₃-1))
  + ½ C₃ ((λ₁λ₂-1)² + (λ₁λ₃-1)² + (λ₂λ₃-1)²)
  +   C₄ ((λ₁λ₂-1)(λ₁λ₃-1) + (λ₁λ₂-1)(λ₂λ₃-1) + (λ₁λ₃-1)(λ₂λ₃-1))
  + ½ C₅ (λ₁λ₂λ₃-1)²

甚至讓兩者彈性係數相同。以便讓數學式子更清爽。

Ψ = ½ C₁ ε₁² + ½ C₂ ε₂² + ½ C₃ ε₃²

ε₁ = (λ₁-1) + (λ₂-1) + (λ₃-1)
ε₂ = (λ₁λ₂-1) + (λ₁λ₃-1) + (λ₂λ₃-1)
ε₃ = λ₁λ₂λ₃-1

isotropic strain energy density可以改寫成特徵方程式的係數。物理術語是invariants of tensor。

Ψ = ½ C₁ (I₁-3)² + ½ C₂ (I₂-3)² + ½ C₃ (I₃-1)²

I₁ = λ₁ + λ₂ + λ₃       = tr(S)
I₂ = λ₁λ₂ + λ₁λ₃ + λ₂λ₃ = ½ (tr(S)² - tr(S²))
I₃ = λ₁λ₂λ₃             = det(S)

以上就是超彈性的基本功。接下來花招百出、群魔亂舞。

strain energy density
物理學家創造的數學公式

物理學家發明各式各樣的strain density energy。引用Green strain，配合Lamé's parameters，聚集奇幻要素。

Saint Venant–Kirchhoff material
Ψ = ½ λ tr(Ε)² + μ tr(Ε²)

neo-Hookean material
Ψ = μ tr(Ε) - μ log(det(F)) + ½ λ log²(det(F))

Ogden material
Ψ = sum μ/k (λ₁ᵏ + λ₂ᵏ + λ₃ᵏ - 3)
     ᵏ

物理學家發明Green strain，套用matrix trace，得到特徵值的平方和。出招之前要喊出華麗的招式名稱。

Cauchy infinitesimal strain
ε = ½((F-I)+(F-I)ᵀ) = ½(∇u + (∇u)ᵀ)

Green finite strain
Ε = ½(FᵀF-I) = ½(∇u + (∇u)ᵀ + (∇u)ᵀ∇u)
^^
大寫希臘字母Ε，唸作/ˈɛpsɪlɒn/，寫作epsilon。不是大寫英文字母E。

trace of Cauchy strain
tr(ε) = tr(F-I) ≠ (λ₁-1) + (λ₂-1) + (λ₃-1)

trace of Green strain
2 tr(Ε) = tr(FᵀF-I) = (λ₁²-1) + (λ₂²-1) + (λ₃²-1)

特徵值來自拉伸矩陣。拉伸矩陣來自極分解。拉伸矩陣的奇異值等於特徵值。

F = (UVᵀ)(VΣVᵀ) = RS     polar decomposition
FᵀF = VΣ²Vᵀ
FᵀF-I = V(Σ²-I)Vᵀ

物理學家利用deformation gradient，套用matrix determinant與log()，得到特徵值的對數和。出招之前要喊出華麗的招式名稱。

F = (UVᵀ)(VΣVᵀ) = RS     polar decomposition
det(F) = det(RS) = det(S) = λ₁λ₂λ₃
log(det(F)) = log(λ₁λ₂λ₃) = log(λ₁) + log(λ₂) + log(λ₃)

ハイパーエラスティシティ～超弾性の幻想譚～

strain energy density
計算學家創造的數學公式

物理學家喜歡喊matrix trace，計算學家喜歡喊matrix norm。然而兩者並不相等。當矩陣是normal matrix，兩者才會相等。幸好拉伸矩陣是normal matrix的其中一種特例。大家愛喊哪種都行。

嚴謹起見，下述數學式子，一律保留大於等於符號，即使相等。

[Chao–Pinkall–Sanan–Schröder 2010]

Ψ(F) = min  ∫  ‖Fp - Rp‖²   continuous rigid alignment
        R  p∈Volume         solution is Laplace's equation
                            Lcot p = 0

Ψ(F) = min sum ‖Fp - Rp‖²   discrete rigid alignment
        R  p∈Vertices       solution is polar decomposition
                            F = RS

Ψ(F) = ‖F - R‖²             an approximation (I am not sure)
                            R is polar decomposition F = RS

Ψ(F) = sum (σᵢ - 1)²        an advanced approximation
                            σᵢ are singular values F = UΣVᵀ

    ‖S‖²              Frobenius norm: squared sum of elements
  ≥ λ₁² + λ₂² + λ₃²   https://math.stackexchange.com/questions/620870/
  = σ₁² + σ₂² + σ₃²   squares are positive

    ‖F - R‖²          Frobenius norm
  = ‖RS - R‖²         polar decomposition
  = ‖R(S - I)‖²
  = ‖S - I‖²          orthonormal matrix R is length preserving
  ≥ sum (λᵢ - 1)²     eigenvalue shift
  = sum (σᵢ - 1)²

   原始論文F := df , S := Y
   原始論文將上式再分拆成normal和shear。可是2ab那項不見了。

[McAdams et al. 2011]

Ψ(F) = μ ‖F - R‖² + ½ λ tr(RᵀF − I)²
       ^^^^^^^^^^   ^^^^^^^^^^^^^^^^
      squared term    full term

     = μ ‖S - I‖² + ½ λ tr(S − I)²
       ^^^^^^^^^^   ^^^^^^^^^^^^^^
      squared term    full term

     ≥ μ sum (σᵢ - 1)² + ½ λ (sum (σᵢ - 1))²
       ^^^^^^^^^^^^^^^   ^^^^^^^^^^^^^^^^^^^
        squared term          full term

    ‖S‖²              Frobenius norm: squared sum of elements
  ≥ λ₁² + λ₂² + λ₃²   https://math.stackexchange.com/questions/620870/
  = σ₁² + σ₂² + σ₃²   squares are positive

    ‖S - I‖²
  ≥ sum (σᵢ - 1)²     eigenvalue shift

    tr(S)             matrix trace: sum of diagonal elements
  = λ₁ + λ₂ + λ₃      https://math.stackexchange.com/questions/3018616/
  = σ₁ + σ₂ + σ₃      all eigenvalues are positive
                      since S is positive-definite
    tr(S - I)²
  = (sum (σᵢ - 1))²   eigenvalue shift

[Stomakhin et al. 2012] [Stomakhin et al. 2013]

Ψ(F) = μ ‖F - R‖² + ½ λ ‖det(F) - 1‖²
       ^^^^^^^^^^   ^^^^^^^^^^^^^^^^^
         strain        bulk strain

     ≥ μ sum (σᵢ - 1)² + ½ λ (σ₁σ₂σ₃ - 1)²
       ^^^^^^^^^^^^^^^   ^^^^^^^^^^^^^^^^^
            strain          bulk strain

    det(F)            volumetric scaling of deformation
  = det(RS)           polar decomposition
  = det(R)det(S)      https://math.stackexchange.com/questions/60284/
  = det(S)            det(R) = +1 if no reflection
  = λ₁λ₂λ₃            scaling of eigenbasis
  = σ₁σ₂σ₃            all eigenvalues are positive
                      since S is positive-definite

計算學家的strain energy density，同樣也是毫無邏輯。

放飛自我。無限可能。

first Piola–Kirchhoff stress

stress還可以細分為兩種：變形前、變形後。

P                first Piola-Kirchhoff stress
N                normal vector (of initial surface)
S                area          (of initial surface)
∂f/∂S = P N      force density (of initial surface)

σ                Cauchy stress
n                normal vector (of current surface)
s                area          (of current surface)
∂f/∂s = σ n = t  Cauchy traction vector

Nanson's formula：變形前後，兩種表面積（向量）的關係式。

∂s n = det(F) F⁻ᵀ ∂S N     Nanson's formula

F     deformation gradient
X     length
V     volume

∂x = F ∂X
∂v = det(F) ∂V
∂V = ∂Xₓ ∂X₝ ∂X₞ = (∂S N) ∙ ∂X
∂v = ∂xₓ ∂x₝ ∂x₞ = (∂s n) ∙ ∂x

   (∂s n) ∙ ∂x     = det(F) (∂S N) ∙ ∂X
   (∂s n) ∙ (F ∂X) = det(F) (∂S N) ∙ ∂X
(Fᵀ ∂s n) ∙ ∂X     = det(F) (∂S N) ∙ ∂X
   (∂s n) ∙ ∂X     = det(F) (F⁻ᵀ ∂S N) ∙ ∂X
    ∂s n           = det(F)  F⁻ᵀ ∂S N

Piola transformation：變形前後，兩種應力的關係式。

σ = P Fᵀ / det(F)     Piola transformation

∂f/∂S = P N  =>  ∂f = P N ∂S        first Piola-Kirchhoff stress
∂f/∂s = σ n  =>  ∂f = σ n ∂s        Cauchy stress
σ n ∂s = P N ∂S
σ det(F) F⁻ᵀ ∂S N = P ∂S N          Nanson's formula
σ det(F) F⁻ᵀ      = P
σ                 = P det(F)⁻¹ Fᵀ

first Piola–Kirchhoff stress另一種定義方式

    ∂Ψ
P = ——
    ∂F

按照stain energy density和first Piola–Kirchhoff stress的原始定義，這個公式顯然是錯的！

這件事情很容易解決。既然stain energy density都可以隨便喊了，那麼first Piola–Kirchhoff stress當然也可以隨便喊囉。物理學家直接聲稱這是定義。這樣就沒問題了。

身穿水手服、手握日本刀，那麼飛身砍子彈就是基本常識。

有些人使用此定義，配合Piola transformation求得應力，再求得力密度。

[Jiang–Gast–Teran 2017]

       1            1   ∂Ψ
σ = —————— PFᵀ = —————— —— Fᵀ
    det(F)       det(F) ∂F

∂f
—— = ∇∙σ
∂V

有些人並未使用此定義。能量密度對位置微分求得力密度。沒有引入first Piola–Kirchhoff stress。

[Stomakhin et al. 2013]

    ∂U           ∂U
f = ——  and  Ψ = ——     (initial coordinates X)
    ∂X           ∂V     (current coordinates x)

∂f   ∂Ψ   ∂Ψ ∂F
—— = —— = —— ——
∂V   ∂X   ∂F ∂X

不知名數學公式：來自這份教材。

Ψ̇ = P : Ḟ = σ : L = S : Ε̇

strain energy density         Ψ
strain power density          Ψ̇ = ∂Ψ/∂t
deformation                   x
deformation gradient          F = ∂x/∂X
deformation gradient rate     Ḟ = ∂F/∂t
velocity gradient             ∇x = ∂v/∂X
velocity gradient             L = ∂v/∂x
Cauchy strain                 ε = ((F-I)+(F-I)ᵀ)/2
Green strain                  Ε = (FᵀF - I)/2
Green deformation             C = FᵀF
Young's modulus               E
Cauchy stress                 σ = Eε
first Piola–Kirchhoff stress  P = ∂Ψ/∂F   ✘
second Piola–Kirchhoff stress S = ∂Ψ/∂C   ✘
double dot product            :

cloth

布料。習慣採用spring network model。畢竟織物結構差不多就是長那樣。

http://www.cs.cornell.edu/projects/YarnCloth/
http://www.cs.columbia.edu/cg/wetcloth/

thin shell

薄殼、細線，需要細心調整應力。

專著《Elasticity and Geometry: From Hair Curls to the Non-linear Response of Shells》。

《The Material Point Method for Simulation of Thin Membranes》將渦度也納入計算。

https://math.unm.edu/~sulsky/papers/pub.html

strain       e     = (∇u + (∇u)ᵀ) / 2
strain rate  de/dt = (∇v + (∇v)ᵀ) / 2
vorticity    W     = (∇v - (∇v)ᵀ) / 2     

《Discrete Elastic Rods》採用了完全不同的策略，使用了離散微分幾何。

http://ddg.cs.columbia.edu/SIGGRAPH05/Shells.pdf

deformation mapping:  x̕ = f(x)       transformation of point
deformation gradient: t̕ = ∇f(t)      transformation of tangent vector
strain energy:        ‖t̕‖² - ‖t‖²    difference of squared length

  ‖t̕‖² - ‖t‖²
= ‖∇f(t)‖² - ‖t‖²
= tᵀ (∇f)ᵀ∇f t - tᵀt
= tᵀ ((∇f)ᵀ∇f - I) t

其他模擬

運動模擬，已經介紹了四種基本款式。

Newton's laws of motion：牛頓搞定質點。

Euler's laws of motion：歐拉搞定剛體。

hydrodynamic equation：聖維南搞定流體。

Cauchy's laws of motion：柯西搞定柔體。

運動模擬，還有許多進階主題。我試著整理其中幾個。

thermodynamics與heat transfer simulation

熱力學與熱流模擬。物體內部的溫度傳遞。

經典應用是工業設計。例如塑膠製品的吹氣成型、射出成型。加熱塑膠以便塑造形狀，冷卻塑膠以便固定形狀。流動速度與溫度變化，影響了結構與造型。變化太快容易斷裂破損，變化太慢容易擁塞變形。事先利用電腦進行模擬，找到最佳流動策略、最佳產品造型。

blow molding
https://ch.moldex3d.com/products/university/
Energy2D
http://energy.concord.org/

aerodynamics與air flow simulation

空氣動力學與氣流模擬。顧名思義。

經典應用是工業設計。汽機車排氣管、風洞測試，諸如此類的。

fracture mechanics / damage mechanics

破裂力學。一個物體變成多個物體。

破損力學。一個物體形狀改變。

經典應用是材料分析。擋土牆、防彈衣，諸如此類的。

von Mises model
http://www.labmec.org.br/workshops/workshop_2012/

granular dynamics / contact mechanics

顆粒動力學。多個物體互相堆疊。

接觸力學。多個物體互相推擠。

經典應用是大地工程。土石流、輸送管，諸如此類的。

multibody simulation

多體模擬。多個物體，進行連動。

經典應用是機械設計、建築結構設計、人體工學設計。估計機械工作效率。展示機械如何組裝、如何運作。預判建築穩固程度。

https://rapier.rs/
https://nphysics.org/
https://eric-heiden.github.io/video2sim/
https://github.com/deepmind/mujoco
https://drake.mit.edu/
https://www.imagwiki.nibib.nih.gov/content/computational-biomechanics-tools    

articulated body simulation

關節模擬。多個物體，以關節相接，進行連動。

經典演算法是Featherstone's algorithm，但是我沒有研究。

Hellgineers
https://johanpeitz.itch.io/hellgineers
ragdoll physics
https://en.wikipedia.org/wiki/Ragdoll_physics
lubrication system simulation
https://www.google.com/search?q=lubrication+system+simulation

crowd simulation

群眾模擬。大量人群聚集走動。

經典應用是建築設計。判斷人群疏散需要多少時間，並且找出館場裡面容易擁塞的地方。

進階主題是steering behaviors：根據角色的位置及速率，進而採取行動，讓角色有著智慧。

http://gamma.cs.unc.edu/DCrowd/
http://gamma.cs.unc.edu/PLE/
http://mrl.snu.ac.kr/research/ProjectMorphableCrowds/MorphableCrowds.html
http://web-ext.u-aizu.ac.jp/~shigeo/research/formation/