triangulation
triangulation
平面上散布許多點。只以這些點作為三角形頂點,用線段連接產生三角形,三角形數量越多越好。所有線段形成一個「三角剖分」,通常有許多種。

因為三角形數量越多越好,所以三角剖分的外圍一定是凸包。
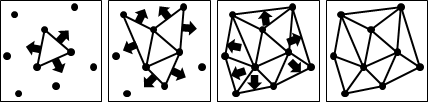
三角形的建構順序、建構地點都相當自由,也因此各種凸包演算法都可以順便求得三角剖分。
三角剖分的三角形個數、邊數
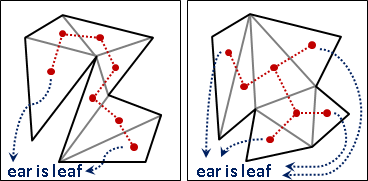
計算凸包的三角剖分,再用剩下的點遞迴分割所在的三角形,最後處理共線的點。
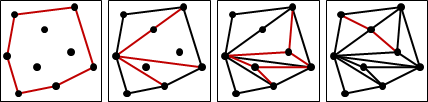
令h是凸包點數,令k是其餘點數。凸包的三角剖分得到h-2個三角形;剩下的點,逐次用於三角剖分,每次都多出兩個三角形。由此可知,無論三角剖分長相如何,一個三角剖分固定有(h-2)+2k個三角形,是O(N)。
同理可知,無論三角剖分長相如何,一個三角剖分固定有(2h-3)+3k條邊,亦是O(N)。
這也呼應了平面圖歐拉公式v-e+f=2。
三角剖分的數量
計算不同的三角剖分有多少種,目前除了窮舉法以外沒有更好的演算法,也無人知道這是P問題抑或是NP-complete問題。
flip graph
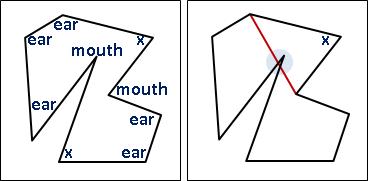
一個三角剖分,翻轉一條邊,可以得到另一個三角剖分。注意到並不是每一條邊都能翻轉的。
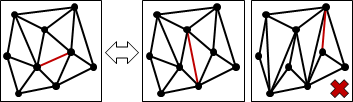
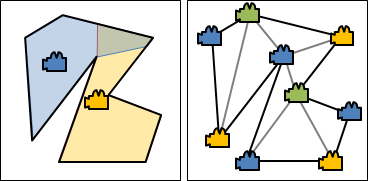
二維平面上,給定一個點集合,把所有三角剖分依照翻轉關係連接成一張無向圖,稱作flip graph,是連通的。
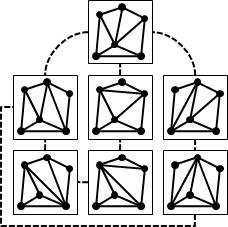
flip graph有著許多謎團,例如點到點最短路徑(兩個三角剖分之間的最少翻轉次數)、直徑、連接性,目前都沒有演算法。
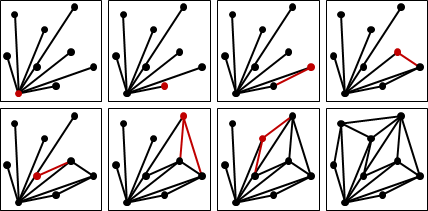
演算法(Graham's scan)
仿照「convex hull: Graham's scan」,掃除凸包頂點的過程即可進行三角剖分。一如既往,共線的點不好處理。時間複雜度O(NlogN),主要取決於排序的時間。
演算法(incremental method)
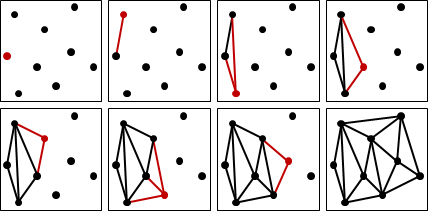
仿照「convex hull: incremental algorithm」,如果當前輸入點在三角形內部,則直接連線至三角形頂點;如果當前輸入點在所有三角形外部,則連線至凸包的切點與凹點。要小心當前輸入點在三角形上的情況。時間複雜度O(N²)。
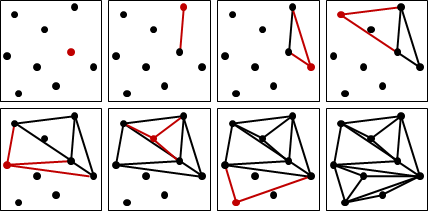
預先按照XY座標排序所有點(平移的掃描線),就能保證當前輸入點都在所有三角形外部。
當前輸入點與凹點的連線,不超過三角剖分的邊數O(N)。當前輸入點與切點的連線,等同Andrew's monotone chain。總時間複雜度O(NlogN)。
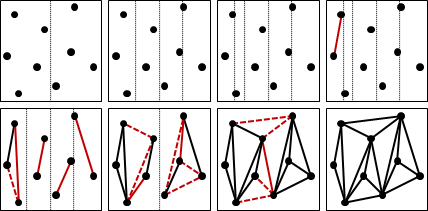
演算法(divide-and-conquer method)
仿照「convex hull: divide-and-conquer method」,尋找外公切線的過程即可合併左右兩個三角剖分。時間複雜度O(NlogN)。
minimum weight triangulation
線段長度總和最小。NP-hard。是否為NP-complete仍是懸案。
用途是節省印刷墨水。
maxmin angle triangulation
最小的角盡量大。時間複雜度O(NlogN)。
minmax angle triangulation
最大的角盡量小。時間複雜度O(N²logN)。
《An O(n² log n) time algorithm for the minmax angle triangulation》
tetrahedralization
「四面體剖分」。三角剖分推廣到三維空間。
四面體剖分的flip graph目前完全不知道長什麼樣。
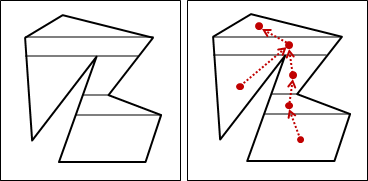
有些形狀不存在四面體剖分,例如Schönhardt polyhedron:三角柱扭轉凹陷。