multivariate function - 演算法筆記

multivariate root finding

multivariate root finding（nonlinear equation）

「多變量求根」。多變量函數求根。

輸出變成多個數值，衍生一個問題：如何求斜率？

導數們從上到下、從左到右依序併成矩陣。細節請見後面章節。

       ⎡ f₁(x) ⎤
F(x) = ⎢ f₂(x) ⎥
       ⎣ f₃(x) ⎦

        ∂         ⎡   |      |      |    ⎤
F′(x) = —— F(x) = ⎢ f₁′(x) f₂′(x) f₃′(x) ⎥
        ∂x        ⎣   |      |      |    ⎦

演算法（ℝ⇨ℝ Newton's method）

從頭複習一遍牛頓法吧。

座標(x, f(x))的切線，與座標軸相交之處，作為下一個x。

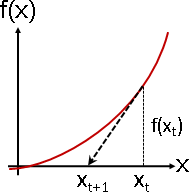
斜率是直除以橫。得到一道等式。

高度f(xₜ)，除以跨距(xₜ - xₜ₊₁)，得到切線斜率f′(xₜ)。

f′(xₜ) = f(xₜ) / (xₜ - xₜ₊₁)

只有乘法，沒有除法。

f′(xₜ) (xₜ - xₜ₊₁) = f(xₜ)

移項整理，提出xₜ₊₁。得到牛頓法公式。

xₜ₊₁ = xₜ - f(xₜ) / f′(xₜ)

時間複雜度O(T)，T是遞推次數。

演算法（ℝⁿ⇨ℝ Newton's method）

牛頓法，推廣成許多個輸入變數。

斜率推廣成梯度。切線推廣成切面。交點推廣成交線。

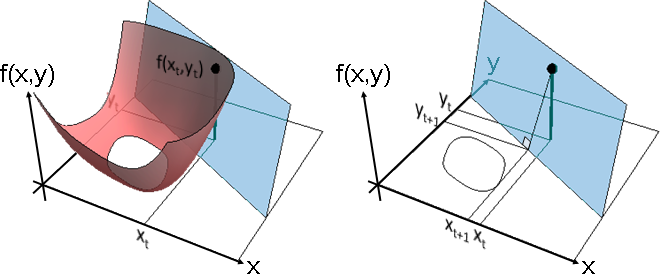
k[x_, y_] := Sqrt[(1.5*x*x*x)^2] + Sqrt[(2*y*y*y)^2] + 0.5*x*y - 0.05; f[x_, y_] := k[x + .4, y + .3]; x0 = .5 - .4; y0 = .65 - .3; f0 = f[x0,y0]; gx0 = N[Derivative[1,0][f][x0,y0]]; gy0 = N[Derivative[0,1][f][x0,y0]]; xyplane = Graphics3D[{Opacity[0], Polygon[{{-1,-1,0},{-1,1,0},{1,1,0},{1,-1,0}}]}, Boxed -> False (*, ViewPoint -> {0, 0, -Infinity}*) ]; func = Plot3D[f[x,y], {x, -1, 1}, {y, -1, 1}, PlotRange -> {-1, 1}, ClippingStyle -> None, Mesh -> None, PlotStyle->Opacity[0.8], RegionFunction -> Function[{x, y, z}, 0 <= z <= 1], ColorFunction -> (ColorData["CherryTones"][Rescale[#3, {-2, 2}]] &)]; plane = Plot3D[gx0*(x-x0)+gy0*(y-y0)+f0, {x, -1, 1}, {y, -1, 1}, Mesh -> None, PlotStyle -> Opacity[0.8], ColorFunction -> (RGBColor[0,112,192] &), RegionFunction -> Function[{x, y, z}, 0 <= z <= 1]]; root = Plot3D[0, {x, -1, 1}, {y, -1, 1}, PlotRange -> {-1, 1}, PlotStyle -> Opacity[0], Mesh -> None, RegionFunction -> Function[{x, y, z}, f[x,y] > 0]]; levelset = SliceContourPlot3D[f[x,y], z == 0, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, PlotRange -> {-1, 1}, Contours -> Table[i,{i,0,1,0.1}], ContourShading -> None, ContourStyle -> LightGray, BoundaryStyle -> LightGray]; x0bar = Graphics3D[{Black, Line[{{x0, -1, 0},{x0, y0, 0}}]}]; y0bar = Graphics3D[{Black, Line[{{-1, y0, 0},{x0, y0, 0}}]}]; f0bar = Graphics3D[{Thickness[0.01], CapForm["Butt"], Black, Line[{{x0, y0, 0},{x0, y0, f0}}]}]; f0point = Graphics3D[{Black, Sphere[{x0, y0, f0}, 0.05]}]; x1 = x0 - f0 * gx0 / ((gx0 ^ 2) + (gy0 ^ 2)); y1 = y0 - f0 * gy0 / ((gx0 ^ 2) + (gy0 ^ 2)); x1bar = Graphics3D[{Black, Line[{{x1, -1, 0},{x1, y1, 0}}]}]; y1bar = Graphics3D[{Black, Line[{{-1, y1, 0},{x1, y1, 0}}]}]; line = Graphics3D[{Black, Line[{{x0, y0, f0},{x1, y1, 0}}]}]; xs = -f0 / gx0 + x0; ys = -f0 / gy0 + y0; xsline = Graphics3D[{Black, Line[{{xs, y0, 0},{x0, y0, f0}}]}]; ysline = Graphics3D[{Black, Line[{{x0, ys, 0},{x0, y0, f0}}]}]; xspoint = Graphics3D[{Black, Sphere[{xs, y0, 0}, 0.05]}]; yspoint = Graphics3D[{Black, Sphere[{x0, ys, 0}, 0.05]}];

Show[xyplane,func,plane,f0point,f0bar,x0bar,y0bar] (* RGBColor[168,206,234] *) Show[xyplane,plane,f0point,f0bar,x0bar,y0bar,x1bar,y1bar,line] Show[xyplane,root,plane]

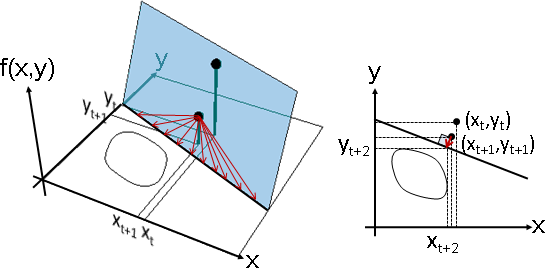
X方向切線與XY平面的交點、Y方向切線與XY平面的交點，兩交點連線，得到交線。

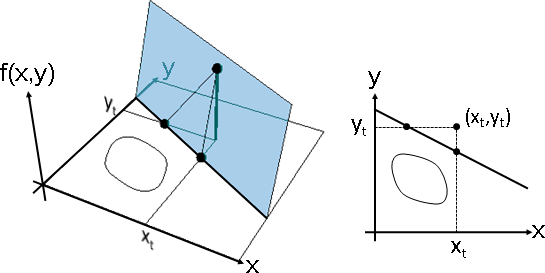
Show[xyplane,plane,f0point,f0bar,x0bar,y0bar,xsline,ysline,xspoint,yspoint] Show[xyplane,func,plane] (* ViewPoint -> {0, 0, -Infinity} *)

切面上有許多切線，可以作為前進方向；交線上有許多點，可以作為下一個x。牛頓法選擇了最短切線：垂直於交線。

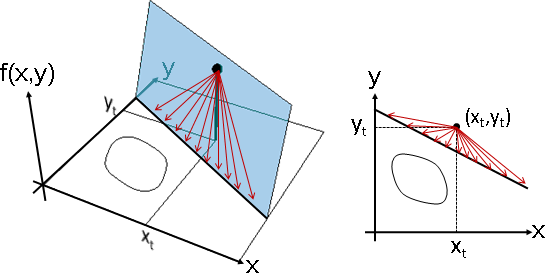
Show[xyplane,plane,f0point,f0bar,x0bar,y0bar]

最短切線一定是梯度方向。等高線的垂直方向。

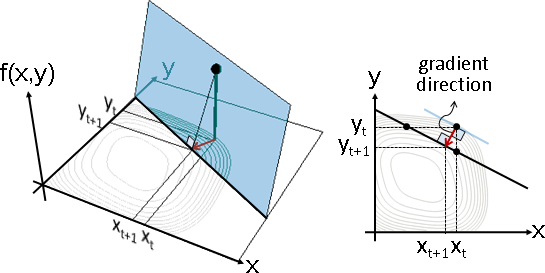
Show[xyplane,plane,levelset,f0point,f0bar,x0bar,y0bar,x1bar,y1bar,line] ContourPlot[f[x,y], {x, -1, 1}, {y, -1, 1}, Frame -> False, ContourShading -> None, Contours -> Table[i,{i,0,1,0.1}]]

接下來把上述概念寫成數學式子。

乘法推廣成點積。得到所有切線。

∇f(xₜ)ᵀ (xₜ - xₜ₊₁) = f(xₜ)

除法推廣成點積反運算（虛擬反矩陣）。得到最短切線。

                               ∇f(xₜ) f(xₜ)    ∇f(xₜ) f(xₜ) 
(xₜ - xₜ₊₁) = ∇f(xₜ)ᵀ⁺ f(xₜ) = ———————————— = ——————————————
                                 ‖∇f(xₜ)‖²    ∇f(xₜ)ᵀ ∇f(xₜ)

移項整理，提出xₜ₊₁。得到牛頓法公式。

                                   ∇f(xₜ) f(xₜ) 
xₜ₊₁ = xₜ - ∇f(xₜ)ᵀ⁺ f(xₜ) = xₜ - ——————————————
                                  ∇f(xₜ)ᵀ ∇f(xₜ)

時間複雜度O(NT)，N是變數數量，T是遞推次數。

演算法（ℝⁿ⇨ℝᵐ Newton's method）

牛頓法，推廣成多變量函數。

F′(xₜ)ᵀ (xₜ - xₜ₊₁) = F(xₜ)
(xₜ - xₜ₊₁) = F′(xₜ)ᵀ⁺ F(xₜ)
xₜ₊₁ = xₜ - F′(xₜ)ᵀ⁺ F(xₜ)

改寫成Jacobian matrix風格。

xₜ₊₁ = xₜ - J(xₜ)⁺ F(xₜ)     where J(xₜ) = F′(xₜ)ᵀ

時間複雜度O(N³T)，N是變數數量與函數數量較大者，T是遞推次數。

演算法（ℝ⇨ℝ secant method）

從頭複習一遍割線法吧。

座標(x₁, f(x₁))與(x₂, f(x₂))的割線，與座標軸相交之處，作為下一個x。

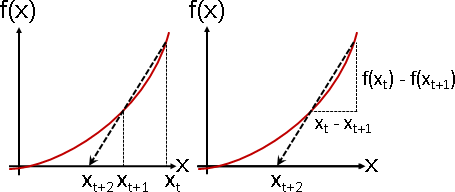
牛頓法是切線斜率f′(xₜ)。割線法是割線斜率sₜ。

Newton's method
f′(xₜ) = f(xₜ) / (xₜ - xₜ₊₁)

secant method
⎰ sₜ = (f(xₜ₋₁) - f(xₜ)) / (xₜ₋₁ - xₜ)
⎱ sₜ = (f(xₜ) - 0) / (xₜ - xₜ₊₁)

只有乘法，沒有除法。

⎰ sₜ (xₜ₋₁ - xₜ) = f(xₜ₋₁) - f(xₜ)
⎱ sₜ (xₜ - xₜ₊₁) = f(xₜ) - 0

二式移項整理，提出xₜ₊₁。

xₜ₊₁ = xₜ - f(xₜ) / sₜ

一式代入二式，得到割線法公式。

xₜ₊₁ = xₜ - f(xₜ) (xₜ₋₁ - xₜ) / (f(xₜ₋₁) - f(xₜ))

改寫成跨距風格。負負得正。

xₜ₊₁ = xₜ - f(xₜ) Δxₜ / Δfₜ     where Δxₜ = xₜ - xₜ₋₁
                                      Δfₜ = f(xₜ) - f(xₜ₋₁)

時間複雜度O(T)，T是遞推次數。

演算法（ℝⁿ⇨ℝ secant method）

割線法，推廣成許多個輸入變數。

斜率推廣成梯度。割線推廣成割面。交點推廣成交線。

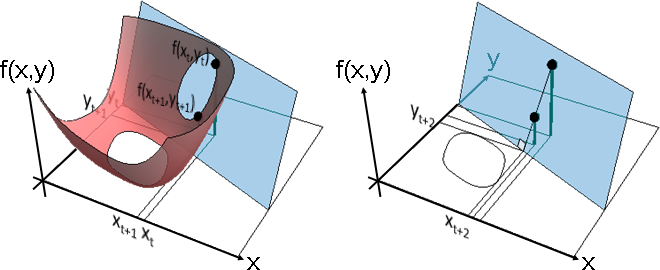
k[x_, y_] := Sqrt[(1.5*x*x*x)^2] + Sqrt[(2*y*y*y)^2] + 0.5*x*y - 0.05; f[x_, y_] := k[x + .4, y + .3]; x0 = .5 - .4; y0 = .65 - .3; f0 = f[x0,y0]; x1 = .425 - .4; y1 = .45 - .3; f1 = f[x1,y1]; dx = x0 - x1; dy = y0 - y1; df = f0 - f1; d = (dx ^ 2) + (dy ^ 2); gx1 = df * dx / d; gy1 = df * dy / d; g1 = (gy1 ^ 2) + (gx1 ^ 2); x2 = x1 - f1 * gx1 / g1; y2 = y1 - f1 * gy1 / g1; t[x_, y_] := gx1*(x-x1) + gy1*(y-y1) + f1; x0bar = Graphics3D[{Black, Line[{{x0, -1, 0},{x0, y0, 0}}]}]; y0bar = Graphics3D[{Black, Line[{{-1, y0, 0},{x0, y0, 0}}]}]; f0bar = Graphics3D[{Thickness[0.01], CapForm["Butt"], Black, Line[{{x0, y0, 0},{x0, y0, f0}}]}]; f0point = Graphics3D[{Black, Sphere[{x0, y0, f0}, 0.05]}]; x1bar = Graphics3D[{Black, Line[{{x1, -1, 0},{x1, y1, 0}}]}]; y1bar = Graphics3D[{Black, Line[{{-1, y1, 0},{x1, y1, 0}}]}]; f1bar = Graphics3D[{Thickness[0.01], CapForm["Butt"], Black, Line[{{x1, y1, 0},{x1, y1, f1}}]}]; f1point = Graphics3D[{Black, Sphere[{x1, y1, f1}, 0.05]}]; x2bar = Graphics3D[{Black, Line[{{x2, -1, 0},{x2, y2, 0}}]}]; y2bar = Graphics3D[{Black, Line[{{-1, y2, 0},{x2, y2, 0}}]}]; line = Graphics3D[{Black, Line[{{x0, y0, f0},{x2, y2, 0}}]}]; xyplane = Graphics3D[{Opacity[0], Polygon[{{-1,-1,0},{-1,1,0},{1,1,0},{1,-1,0}}]}, Boxed -> False (*, ViewPoint -> {0, 0, -Infinity}*) ]; func = Plot3D[f[x,y], {x, -1, 1}, {y, -1, 1}, PlotRange -> {-1, 1}, ClippingStyle -> None, Mesh -> None, PlotStyle->Opacity[0.8], RegionFunction -> Function[{x, y, z}, 0 <= z <= 1], ColorFunction -> (ColorData["CherryTones"][Rescale[#3, {-2, 2}]] &)]; plane = Plot3D[t[x,y], {x, -1, 1}, {y, -1, 1}, Mesh -> None, PlotStyle -> Opacity[0.8], ColorFunction -> (RGBColor[0,112,192] &), RegionFunction -> Function[{x, y, z}, 0 <= z <= 1]]; intersect = Plot3D[t[x,y]+0.02, {x, -1, 1}, {y, -1, 1}, Mesh -> None, PlotStyle -> Opacity[0.8], ColorFunction -> (RGBColor[0,112,192] &), RegionFunction -> Function[{x, y, z}, z >= f[x,y]+0.02]];

Show[xyplane,func,plane,intersect,x0bar,y0bar,f0bar,f0point,x1bar,y1bar,f1bar,f1point] (* RGBColor[168,206,234] *) Show[xyplane,plane,x0bar,y0bar,f0bar,f0point,x1bar,y1bar,f1bar,f1point,x2bar,y2bar,line]

兩點之間有許多割面。割線法選擇了最正割面：其交線垂直於兩點連線。

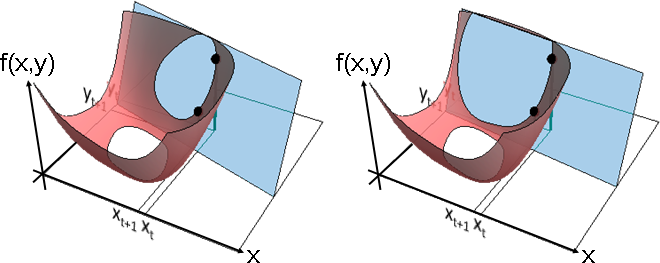
par = LinearSolve[{{x0, y0, 1}, {x1, y1, 1}, {x0 - 0.07, 0, 1}}, {f0, f1, 0}]; par = LinearSolve[{{x0, y0, 1}, {x1, y1, 1}, {x0 + 0.005, 0, 1}}, {f0, f1, 0}]; planebad = Plot3D[(par[[1]]*x)+(par[[2]]*y)+par[[3]], {x, -1, 1}, {y, -1, 1}, Mesh -> None, PlotStyle -> Opacity[0.8], ColorFunction -> (RGBColor[0,112,192] &), RegionFunction -> Function[{x, y, z}, 0 <= z <= 1]]; intersectbad = Plot3D[(par[[1]]*x)+(par[[2]]*y)+par[[3]]+0.02, {x, -1, 1}, {y, -1, 1}, Mesh -> None, PlotStyle -> Opacity[0.8], ColorFunction -> (RGBColor[0,112,192] &), RegionFunction -> Function[{x, y, z}, 1 >= z >= f[x,y]+0.02]]; Show[xyplane,func,planebad,intersectbad,x0bar,y0bar,f0bar,f0point,x1bar,y1bar,f1bar,f1point]

割面上有許多割線，可以作為前進方向；交線上有許多點，可以作為下一個x。割線法選擇了最短割線：垂直於交線。

Show[xyplane,plane,x0bar,y0bar,f0bar,f0point,x1bar,y1bar,f1bar,f1point]

接下來把上述概念寫成數學式子。

點積。得到所有割面。

sₜᵀ (xₜ₋₁ - xₜ) = f(xₜ₋₁) - f(xₜ)

點積反運算（虛擬反矩陣）。得到最正割面。

sₜᵀ = (f(xₜ₋₁) - f(xₜ)) (xₜ₋₁ - xₜ)⁺ = Δfₜ Δxₜ⁺

點積。得到所有割線。

sₜᵀ (xₜ - xₜ₊₁) = f(xₜ)     where sₜᵀ = Δfₜ Δxₜ⁺

點積反運算（虛擬反矩陣）。得到最短割線。

(xₜ - xₜ₊₁) = sₜᵀ⁺ f(xₜ) = (Δfₜ Δxₜ⁺)⁺ f(xₜ) = Δxₜ Δfₜ⁺ f(xₜ)

移項整理，提出xₜ₊₁。得到割線法公式。

xₜ₊₁ = xₜ - Δxₜ Δfₜ⁺ f(xₜ)

然而割線法只會走一直線，往往走不到根。沒人使用割線法。

演算法（ℝⁿ⇨ℝᵐ secant method）

割線法，推廣成多變量函數。

xₜ₊₁ = xₜ - Δxₜ ΔFₜ⁺ F(xₜ)

一樣沒人用。

演算法（Broyden's method）

割線法改良版。不選擇最正割面，避免走一直線。

割線法寫成兩道式子，先改良第一式，再改良第二式。

⎰ Sₜᵀ = (F(xₜ₋₁) - F(xₜ)) (xₜ₋₁ - xₜ)⁺ = ΔFₜ Δxₜ⁺
⎱ xₜ₊₁ = xₜ - Sₜᵀ⁺ F(xₜ)

一、改成遞推更新割面。用前一個割面，求後一個割面。

故意製造Sₜ₋₁。移項整理，提出Sₜ。得到割面遞迴公式。

最初的割面，設定成隨機梯度（隨便亂歪），或者第一點的切面的梯度（不會太歪）。

最初的割面，故意設定成歪的；之後的割面，故意保持是歪的。得以螺旋行進至根。

Sₜᵀ Δxₜ = ΔFₜ
(Sₜ - Sₜ₋₁ + Sₜ₋₁)ᵀ Δxₜ = ΔFₜ
(Sₜ - Sₜ₋₁)ᵀ Δxₜ + Sₜ₋₁ᵀ Δxₜ = ΔFₜ
(Sₜ - Sₜ₋₁)ᵀ Δxₜ = ΔFₜ - Sₜ₋₁ᵀ Δxₜ
(Sₜ - Sₜ₋₁)ᵀ = (ΔFₜ - Sₜ₋₁ᵀ Δxₜ) Δxₜ⁺
Sₜᵀ - Sₜ₋₁ᵀ = (ΔFₜ - Sₜ₋₁ᵀ Δxₜ) Δxₜ⁺
Sₜᵀ = Sₜ₋₁ᵀ + (ΔFₜ - Sₜ₋₁ᵀ Δxₜ) Δxₜ⁺

  Δxₜ⁺
= Δxₜᵀ / ‖Δxₜ‖² 
= Δxₜᵀ / (Δxₜᵀ Δxₜ)

第一式改良完畢，得到計算公式。

⎰ Sₜᵀ = Sₜ₋₁ᵀ + (ΔFₜ - Sₜ₋₁ᵀ Δxₜ) Δxₜ⁺
⎱ xₜ₊₁ = xₜ - Sₜᵀ⁺ F(xₜ)

移項的效果：前後兩個割面，梯度差異盡量小。

min ‖Sₜ - Sₜ₋₁‖²   subject to Sₜᵀ Δxₜ = ΔFₜ

二、改成直接紀錄虛擬反矩陣。避免不斷計算虛擬反矩陣。

令Cₜᵀ = Sₜᵀ⁺。

Sₜᵀ Δxₜ = ΔFₜ
Cₜᵀ ΔFₜ = Δxₜ
(Cₜ - Cₜ₋₁ + Cₜ₋₁)ᵀ ΔFₜ = Δxₜ
(Cₜ - Cₜ₋₁)ᵀ ΔFₜ + Cₜ₋₁ᵀ ΔFₜ = Δxₜ
(Cₜ - Cₜ₋₁)ᵀ ΔFₜ = Δxₜ - Cₜ₋₁ᵀ ΔFₜ
(Cₜ - Cₜ₋₁)ᵀ = (Δxₜ - Cₜ₋₁ᵀ ΔFₜ) ΔFₜ⁺
Cₜᵀ - Cₜ₋₁ᵀ = (Δxₜ - Cₜ₋₁ᵀ ΔFₜ) ΔFₜ⁺
Cₜᵀ = Cₜ₋₁ᵀ + (Δxₜ - Cₜ₋₁ᵀ ΔFₜ) ΔFₜ⁺

  ΔFₜ⁺
= ΔFₜᵀ / ‖ΔFₜ‖²
= ΔFₜᵀ / (ΔFₜᵀ ΔFₜ)

第二式改良完畢，得到計算公式。

⎰ Cₜᵀ = Cₜ₋₁ᵀ + (Δxₜ - Cₜ₋₁ᵀ ΔFₜ) ΔFₜ⁺
⎱ xₜ₊₁ = xₜ - Cₜᵀ F(xₜ)

移項的效果：前後兩個割面，梯度的虛擬反矩陣差異盡量小。

min ‖Cₜ - Cₜ₋₁‖²   subject to Cₜᵀ ΔFₜ = Δxₜ

時間複雜度O(NMT)，N是變數數量，M是函數數量，T是遞推次數。

演算法（fixed point iteration）

不動點遞推法，推廣成多變量函數。

函數和變數必須一樣多個。

xₜ₊₁ = xₜ + λ F(xₜ)

multivariate optimization

multivariate optimization（nonlinear least squares）

「多變量最佳化」。多變量函數最佳化。

輸出變成多個數值，衍生兩個問題：如何比大小？如何求斜率？

比大小有兩種方式：

multiobjective optimization　輸出數值們的加權平均數（非長度函數）
multivariate optimization  　輸出數值們的平方和（長度平方函數）

本文介紹平方和。目標函數是輸出數值們的平方和‖F(x)‖²。

       ⎡ f₁(x) ⎤
F(x) = ⎢ f₂(x) ⎥
       ⎣ f₃(x) ⎦

‖F(x)‖² = F(x)ᵀF(x) = f₁(x)² + f₂(x)² + f₃(x)²

演算法（Newton's method）

一次微分等於零的地方是極值、鞍點。

牛頓法求極值。事先微分，然後求根。

xₜ₊₁ = xₜ - f″(xₜ)ᵀ⁺ f′(xₜ)

目標函數是‖F(x)‖²。

xₜ₊₁ = xₜ - [ ∂²/∂x² ‖F(x)‖² ]ᵀ⁺ [ ∂/∂x ‖F(x)‖² ]     求值就不寫了
xₜ₊₁ = xₜ - [ 2 F″(xₜ)ᵀ F(xₜ) + 2 F′(xₜ) F′(xₜ)ᵀ ]ᵀ⁺ [ 2 F′(xₜ) F(xₜ) ]

時間複雜度取決於二階導數F″(xₜ)。大家投機取巧，避開二階導數，衍生兩種流派。

擬牛頓法（割線法）：用別的東西代替二階導數，例如DFP、BFGS。

高斯牛頓法：直接無視二階導數，例如GN、LM。

演算法（Davidon–Fletcher–Powell algorithm）

Broyden's method求極值。事先微分，然後求根。

注意到二階導數必須是對稱矩陣。

min ‖Sₜ - Sₜ₋₁‖²   subject to Sₜᵀ Δxₜ = ΔFₜ and Sₜᵀ = Sₜ
                                            ^^^^^^^^^^^^

演算法（Broyden–Fletcher–Goldfarb–Shanno algorithm）

Broyden's method求極值。事先微分，然後求根。

改成直接紀錄虛擬反矩陣。避免不斷計算虛擬反矩陣。

min ‖Cₜ - Cₜ₋₁‖²   subject to Cₜᵀ ΔFₜ = Δxₜ and Cₜᵀ = Cₜ
                                            ^^^^^^^^^^^^

演算法（Gauss–Newton algorithm）

牛頓法求極值，但是省略二階導數項，簡化計算過程。

xₜ₊₁ = xₜ - f″(xₜ)ᵀ⁺ f′(xₜ)
xₜ₊₁ = xₜ - [ ∂²/∂x² ‖F(x)‖² ]ᵀ⁺ [ ∂/∂x ‖F(x)‖² ]     求值就不寫了
xₜ₊₁ = xₜ - [ 2 F″(xₜ)ᵀ F(xₜ) + 2 F′(xₜ) F′(xₜ)ᵀ]ᵀ⁺ [ 2 F′(xₜ) F(xₜ) ]
xₜ₊₁ ≈ xₜ - [ 2 F′(xₜ) F′(xₜ)ᵀ ]ᵀ⁺ [ 2 F′(xₜ) F(xₜ) ]   省略二階導數項
xₜ₊₁ ≈ xₜ - [ F′(xₜ) F′(xₜ)ᵀ ]ᵀ⁺ F′(xₜ) F(xₜ)           分子分母同除2
xₜ₊₁ ≈ xₜ - [ F′(xₜ) F′(xₜ)ᵀ ]⁺ F′(xₜ) F(xₜ)            對稱矩陣，省略轉置

改寫成Jacobian matrix風格。

xₜ₊₁ ≈ xₜ - [ J(xₜ)ᵀ J(xₜ) ]⁺ J(xₜ)ᵀ F(xₜ)     ---> xₜ₊₁ = xₜ - (JᵀJ)⁺JᵀF

碰巧是normal equation，精簡成虛擬反矩陣。

xₜ₊₁ ≈ xₜ - J(xₜ)⁺ F(xₜ)     ---> xₜ₊₁ = xₜ - J⁺F

計算公式，完完全全就是牛頓法求根。

ℝ⇨ℝ   求根　 xₜ₊₁ = xₜ -  f(xₜ) / f′(xₜ)
ℝⁿ⇨ℝ  求根　 xₜ₊₁ = xₜ -  f(xₜ) / f′(xₜ)ᵀ = xₜ - J⁺f
ℝⁿ⇨ℝᵐ 求根　 xₜ₊₁ = xₜ -  F(xₜ) / F′(xₜ)ᵀ = xₜ - J⁺F
ℝ⇨ℝ   求極值 xₜ₊₁ = xₜ - f′(xₜ) / f″(xₜ)
ℝⁿ⇨ℝ  求極值 xₜ₊₁ = xₜ - f′(xₜ) / f″(xₜ)ᵀ = xₜ - H⁺f′
ℝⁿ⇨ℝᵐ 求極值 xₜ₊₁ = xₜ - E′(xₜ) / E″(xₜ)ᵀ ≈ xₜ - J⁺F 
註：虛擬反矩陣改寫成矩陣除法風格。
註：E(x) = ‖F(x)‖²

演算法（gradient descent）

不動點遞推法求極值。事先微分，然後求根。

xₜ₊₁ = xₜ - λ f′(xₜ)

目標函數是‖F(x)‖²。

xₜ₊₁ = xₜ - λ [ ∂/∂x ‖F(x)‖² ]
xₜ₊₁ = xₜ - λ [ 2 F′(xₜ) F(xₜ) ]
xₜ₊₁ = xₜ - λ F′(xₜ) F(xₜ)           倍率2併入步伐大小λ

改寫成Jacobian matrix風格。

xₜ₊₁ = xₜ - λ J(xₜ)ᵀ F(xₜ)      ---> xₜ₊₁ = xₜ - λJᵀF

演算法（Levenberg–Marquardt algorithm）

牛頓法求極值：前進方向因地制宜，攻頂路線短。步伐大小不可調整（二階導數的倒數，曲率半徑越大、路線越直、步伐越大），最初只能亦步亦趨。

不動點遞推法求極值：前進方向不可調整（梯度方向），攻頂路線長。步伐大小可以調整，最初就能一步登天。

Gauss–Newton algorithm與gradient descent的前進方向，取加權平均。隨時視情況調整權重，兩害相權取其輕。

xₜ₊₁ = xₜ - (J⁺ + λJᵀ)F
             ^^   ^^^
         Newton   fixpoint

有人將gradient descent做梯度正規化。

JᵀJ的對角線元素，是梯度的每個元素的平方。diag(JᵀJ)將之併成一個向量。diag(JᵀJ)⁺形成倒數，即是梯度正規化──然而他忘了開根號。大家將錯就錯。

xₜ₊₁ = xₜ - (J⁺ + diag(JᵀJ)⁺ λJᵀ)F
             ^^   ^^^^^^^^^^ ^^^
         Newton   normalize  fixpoint

有人從normal equation那道式子下手，寫成另外一種風格。

xₜ₊₁ = xₜ - [JᵀJ + 1/λ diag(JᵀJ)]⁺ JᵀF
             ^^^   ^^^^^^^^^^^^^
          Newton   normalized fixpoint

differential calculus: multivariate function

多變量函數微分

函數對各個變數微分。得到各個導數。

f(x) = (2x₁² + x₁x₂ + x₃²)

∂f               ∂f         ∂f       
——— = 4x₁ + x₂   ——— = x₁   ——— = 2x₃
∂x₁              ∂x₂        ∂x₃

函數對向量微分。導數們從上到下依序併成向量。

                                  ⎡ x₁ ⎤
f(x) = (2x₁² + x₁x₂ + x₃²)    x = ⎢ x₂ ⎥
                                  ⎣ x₃ ⎦

        ∂         ⎡ ∂f/∂x₁ ⎤   ⎡ 4x₁ + x₂ ⎤
f′(x) = —— f(x) = ⎢ ∂f/∂x₂ ⎥ = ⎢ x₁       ⎥
        ∂x        ⎣ ∂f/∂x₃ ⎦   ⎣ 2x₃      ⎦

多個函數，從上到下依序併成一個向量，成為多變量函數。

多變量函數對向量微分。導數們從左到右依序併成矩陣。

       ⎡ f₁(x) ⎤   ⎡ 2x₁² + x₁x₂ + x₃²  ⎤
       ⎢ f₂(x) ⎥   ⎢ x₁x₂ + x₂x₃ + x₃x₁ ⎥
F(x) = ⎢ f₃(x) ⎥ = ⎢ x₁² + x₂² + x₃²    ⎥
       ⎢ f₄(x) ⎥   ⎢ x₁ + x₂ + x₃       ⎥
       ⎣ f₅(x) ⎦   ⎣ x₁ - x₂            ⎦

        ∂         ⎡   |      |      |      |      |    ⎤
F′(x) = —— F(x) = ⎢ f₁′(x) f₂′(x) f₃′(x) f₄′(x) f₅′(x) ⎥
        ∂x        ⎣   |      |      |      |      |    ⎦

                  ⎡ 4x₁+x₂ x₂+x₃ 2x₁ 1  1 ⎤
                = ⎢ x₁     x₁+x₃ 2x₂ 1 -1 ⎥
                  ⎣ 2x₃    x₁+x₂ 2x₃ 1  0 ⎦

多變量函數的長度平方

長度平方：各個函數的平方和。函數向量自身點積。

‖F(x)‖² := F(x)ᵀF(x) = f₁(x)² + f₂(x)² + ... + fₙ(x)²

微分乘法律：前微後不微，前不微後微，兩者相加。

∂                 ∂                  ∂
—— F(x)ᵀG(x) := [ —— F(x) ] G(x) + [ —— G(x) ] F(x)
∂x                ∂x                 ∂x

∂             ∂               ∂
—— xᵀF(x) = [ —— x ] F(x) + [ —— F(x) ] x = F(x) + F′(x)x
∂x            ∂x              ∂x

∂            ∂                  ∂
—— ‖F(x)‖² = —— F(x)ᵀF(x) = 2 [ —— F(x) ] F(x) = 2F′(x)F(x)
∂x           ∂x                 ∂x

微分連鎖律：外微，內微，從右到左連乘。

∂             ∂       ∂
—— F(G(x)) := —— G(x) ————— F(G(x))
∂x            ∂x      ∂G(x)

∂            ∂       ∂
—— ‖F(x)‖² = —— F(x) ————— (F(x))² = (F′(x))(2F(x)) = 2F′(x)F(x)
∂x           ∂x      ∂F(x)

多個函數的一次微分（transpose Jacobian matrix）

多個函數，從上到下依序併成一個向量。

多個函數對向量微分。導數們從左到右依序併成矩陣。

該矩陣是「多個函數的一階導數矩陣」。通常不是方陣。

該矩陣也是Jacobian matrix的轉置矩陣。

    ⎡ f₁ ⎤
F = ⎢ f₂ ⎥
    ⎣ f₃ ⎦

     ∂F   ⎡    |      |      |   ⎤   ⎡ ∂f₁/∂x₁ ∂f₂/∂x₁ ∂f₃/∂x₁ ⎤
F′ = —— = ⎢ ∂f₁/∂x ∂f₂/∂x ∂f₃/∂x ⎥ = ⎢ ∂f₁/∂x₂ ∂f₂/∂x₂ ∂f₃/∂x₂ ⎥
     ∂x   ⎣    |      |      |   ⎦   ⎣ ∂f₁/∂x₃ ∂f₂/∂x₃ ∂f₃/∂x₃ ⎦

          ⎡ —————— ∂f₁/∂x —————— ⎤ᵀ  ⎡ ∂f₁/∂x₁ ∂f₁/∂x₂ ∂f₁/∂x₃ ⎤ᵀ
   = Jᵀ = ⎢ —————— ∂f₂/∂x —————— ⎥ = ⎢ ∂f₂/∂x₁ ∂f₂/∂x₂ ∂f₂/∂x₃ ⎥
          ⎣ —————— ∂f₃/∂x —————— ⎦   ⎣ ∂f₃/∂x₁ ∂f₃/∂x₂ ∂f₃/∂x₃ ⎦

一個函數的二次微分（Hessian matrix）

一次微分（函數的梯度）：函數對向量微分，得到向量。

二次微分（函數的梯度的梯度）：再次對向量微分，得到矩陣。

該矩陣是「一個函數的二階導數矩陣」。一定是對稱矩陣。

該矩陣稱作Hessian matrix。

     ∂f   ⎡ ∂f/∂x₀ ⎤
f′ = —— = ⎢ ∂f/∂x₁ ⎥
     ∂x   ⎣ ∂f/∂x₂ ⎦

     ∂f′   ⎡       |             |             |      ⎤
f″ = ——— = ⎢ ∂(∂f/∂x₀)/∂x  ∂(∂f/∂x₁)/∂x  ∂(∂f/∂x₂)/∂x ⎥
     ∂x    ⎣       |             |             |      ⎦

           ⎡ ∂²f/∂x₀∂x₀ ∂²f/∂x₁∂x₀ ∂²f/∂x₂∂x₀ ⎤
   = H   = ⎢ ∂²f/∂x₀∂x₁ ∂²f/∂x₁∂x₁ ∂²f/∂x₂∂x₁ ⎥
           ⎣ ∂²f/∂x₀∂x₂ ∂²f/∂x₁∂x₂ ∂²f/∂x₂∂x₂ ⎦

二次微分＝原函數的Hessian matrix＝一階導數的transpose Jacobian matrix。由於是對稱矩陣，可以省略轉置。

f″ = H_f = J_f′ᵀ = J_f′

differential calculus: linear function

一次函數微分

一次函數對各個變數微分。得到各個導數。

f(x) = (x₁ + x₂ + x₃)

∂f         ∂f         ∂f     
——— = 1    ——— = 1    ——— = 1
∂x₁        ∂x₂        ∂x₃    

f(x) = (c₁x₁ + c₂x₂ + c₃x₃)

∂f         ∂f         ∂f      
——— = c₁   ——— = c₂   ——— = c₃
∂x₁        ∂x₂        ∂x₃

一次函數對向量微分。導數們從上到下依序併成向量。

                                  ⎡ x₁ ⎤
f(x) = (c₁x₁ + c₂x₂ + c₃x₃)   x = ⎢ x₂ ⎥
                                  ⎣ x₃ ⎦

        ∂         ⎡ ∂/∂x₁ f(x) ⎤   ⎡ c₁ ⎤
f′(x) = —— f(x) = ⎢ ∂/∂x₂ f(x) ⎥ = ⎢ c₂ ⎥
        ∂x        ⎣ ∂/∂x₃ f(x) ⎦   ⎣ c₃ ⎦

∂                                            ∂        
—— yᵀx = y                             --->  —— xy = y
∂x                                           ∂x       

∂                                            ∂        
—— xᵀy = y                             --->  —— yx = y
∂x                                           ∂x       

∂                                            ∂         
—— xᵀx = 2x                            --->  —— x² = 2x
∂x                                           ∂x        
                     when A is
∂                    symmetric               ∂           
—— xᵀAx = (A + Aᵀ) x ========= 2Ax     --->  —— ax² = 2ax
∂x                                           ∂x

多個一次函數，依序併成一個向量。甚至視作矩陣乘法。

多個一次函數對向量微分。導數們從左到右依序併成矩陣。

       ⎡ f₁(x) ⎤   ⎡ a₁x₁ + a₂x₂ + a₃x₃ ⎤   ⎡ a₁ a₂ a₃ ⎤       
       ⎢ f₂(x) ⎥   ⎢ b₁x₁ + b₂x₂ + b₃x₃ ⎥   ⎢ b₁ b₂ b₃ ⎥ ⎡ x₁ ⎤
F(x) = ⎢ f₃(x) ⎥ = ⎢ c₁x₁ + c₂x₂ + c₃x₃ ⎥ = ⎢ c₁ c₂ c₃ ⎥ ⎢ x₂ ⎥
       ⎢ f₄(x) ⎥   ⎢ d₁x₁ + d₂x₂ + d₃x₃ ⎥   ⎢ d₁ d₂ d₃ ⎥ ⎣ x₃ ⎦
       ⎣ f₅(x) ⎦   ⎣ e₁x₁ + e₂x₂ + e₃x₃ ⎦   ⎣ e₁ e₂ e₃ ⎦       
                                                 A         x   

        ∂         ⎡   |      |      |      |      |    ⎤
F′(x) = —— F(x) = ⎢ f₁′(x) f₂′(x) f₃′(x) f₄′(x) f₅′(x) ⎥
        ∂x        ⎣   |      |      |      |      |    ⎦

                  ⎡ a₁ b₁ c₁ d₁ e₁ ⎤
                = ⎢ a₂ b₂ c₂ d₂ e₂ ⎥
                  ⎣ a₃ b₃ c₃ d₃ e₃ ⎦
                          Aᵀ

∂                                            ∂        
—— A x = Aᵀ                            --->  —— ax = a
∂x                                           ∂x       

∂                                            ∂        
—— Aᵀx = A                             --->  —— ax = a
∂x                                           ∂x       

∂                                            ∂              
—— (Ax + b) = Aᵀ                       --->  —— (ax + b) = a
∂x                                           ∂x             

∂         ∂                                  ∂          
—— yᵀAx = —— (yᵀA)x = (yᵀA)ᵀ = Aᵀy     --->  —— axy = ay
∂x        ∂x                                 ∂x

一次函數的長度平方

長度平方：所有元素的平方和。向量自身點積。

‖x‖² := xᵀx       = x₁² + x₂² + x₃² + ... + xₙ²

‖Ax‖² = (Ax)ᵀ(Ax) = (Ax₁)² + (Ax₂)² + (Ax₃)² + ... + (Axₙ)²

微分連鎖律：矩陣連乘是從右到左，連鎖律也是從右到左。

∂             ∂       ∂
—— F(G(x)) := —— G(x) ————— F(G(x))
∂x            ∂x      ∂G(x)

∂          ∂    ∂
—— ‖x‖²  = —— x —— (x)² = (1)(2x) = 2x
∂x         ∂x   ∂x

∂          ∂     ∂
—— ‖Ax‖² = —— Ax ——— (Ax)² = (Aᵀ)(2Ax) = 2AᵀAx
∂x         ∂x    ∂Ax

定義的合理性，可由嚴謹的推導過程證明：

                                      AᵀA is always      
∂          ∂              ∂             symmetric        
—— ‖Ax‖² = —— (Ax)ᵀ(Ax) = —— xᵀ(AᵀA)x ============= 2AᵀAx
∂x         ∂x             ∂x

範例

仿照(ax - b)²。用途是一次迴歸。

minimize ‖Ax - b‖²                  x套用函數之後，跟b的差異盡量小

∂
—— ‖Ax - b‖² = 0                   「一次微分等於零」的地方是極值、鞍點
∂x                                  二次函數、開口向上，必是最小值

  ∂
[ —— (Ax - b) ] [ 2(Ax - b) ] = 0   微分連鎖律
  ∂x

Aᵀ [ 2(Ax - b) ] = 0                微分

Aᵀ A x = Aᵀ b                       同除以2、展開、移項

x = (Aᵀ A)⁻¹ Aᵀ b                   normal equation

仿照(ax)²。用途是直線擬合。

minimize ‖Ax‖²   subject to ‖x‖² = 1   單位向量套用函數之後盡量短

minimize ‖Ax‖² - λ (‖x‖² - 1)       Lagrange multiplier

∂
—— [ ‖Ax‖² - λ (‖x‖² - 1) ] = 0    「一次微分等於零」的地方是極值、鞍點
∂x

2 AᵀA x - 2 λ x = 0                 微分

AᵀA x = λ x                         正解是 AᵀA 最小的特徵值的特徵向量
                                    由於是對稱正定矩陣，也等於奇異向量。

仿照ax²且a > 0。用途是二次型最佳化。

minimize xᵀAx   subject to ‖x‖² = 1 and A is symmetric positive-definite

minimize xᵀAx - λ ( ‖x‖² - 1 )      Lagrange multiplier

∂
—— [ xᵀAx - λ ( ‖x‖² - 1 ) ] = 0   「一次微分等於零」的地方是極值、鞍點
∂x                                  二次函數、開口向上，必是最小值

2 A x - 2 λ x = 0                   微分

A x = λ x                           正解是 A 最小的特徵值的特徵向量
                                    由於是對稱正定矩陣，也等於奇異向量。

微分公式一覽表

多變量函數微分，等於Jacobian matrix的轉置矩陣。

F′(x) = J(x)ᵀ            Jacobian matrix

多變量函數微分、一次函數微分，兩者公式互相對應。F(x)對應Ax，J(x)ᵀ對應Aᵀ。

multivariate function     | linear function     | polynomial func.
——————————————————————————|—————————————————————|—————————————————
∂                         | ∂                   | ∂               
—— F(x) = J(x)ᵀ           | —— Ax = Aᵀ          | —— ax = a       
∂x                        | ∂x                  | ∂x              
                          |                     |                 
∂                         | ∂                   | ∂               
—— (F(x) + b) = J(x)ᵀ     | —— (Ax + b) = Aᵀ    | —— (ax + b) = a 
∂x                        | ∂x                  | ∂x              
                          |                     |                 
∂                         | ∂                   | ∂               
—— yᵀF(x) = J(x)ᵀy        | —— yᵀAx = Aᵀy       | —— axy = ay     
∂x                        | ∂x                  | ∂x              
                          |                     |                 
∂                         | ∂                   | ∂               
—— xᵀF(x) = F(x) + J(x)ᵀx | —— xᵀAx = (A + Aᵀ)x | —— ax² = 2ax    
∂x                        | ∂x                  | ∂x              
                          |                     |                 
∂                         | ∂                   | ∂               
—— ‖F(x)‖² = 2J(x)ᵀF(x)   | —— ‖Ax‖² = 2AᵀAx    | —— (ax)² = 2a²x 
∂x                        | ∂x                  | ∂x

多元函數二次微分，等於Hessian matrix及其轉置矩陣。

f″(x) = J′(x) = H(x)ᵀ = H(x)     Hessian matrix

differential calculus: matrix function

矩陣函數微分

矩陣函數對矩陣微分。導數們依序併成矩陣。

∂                          ∂
—— xᵀAy = xyᵀ              —— tr(XᵀAY) = XYᵀ
∂A                         ∂A

∂                          ∂
—— xᵀAᵀy = (xyᵀ)ᵀ = yxᵀ    —— tr(XᵀAᵀY) = YXᵀ
∂A                         ∂A

矩陣的長度平方

所有元素的平方和。矩陣自身內積的對角線總和。

‖X‖ꜰ² := tr(XᵀX)       = x₁₁² + x₁₂² + x₁₃² + ... + xₙₙ²

∂
—— tr(AX) = Aᵀ
∂X

∂
—— tr(XᵀAX) = (A + Aᵀ)X
∂X

∂          ∂
—— ‖X‖ꜰ² = —— tr(XᵀX) = 2X
∂X         ∂X
                                           AᵀA is always
∂           ∂                ∂               symmetric
—— ‖AX‖ꜰ² = —— tr((AX)ᵀAX) = —— tr(XᵀAᵀAX) ============= 2AᵀAX
∂X          ∂X               ∂X

對角線總和trace的相關性質。

tr(A+B) = tr(A) + tr(B)                     additive
tr(kA) = k tr(A)                            scalar
tr(A) = tr(Aᵀ)                              transpose
tr(AB) = tr(BA)                             commute
tr(ABCD) = tr(DABC) = tr(CDAB) = tr(BCDA)   cyclic

任意矩陣X，乘上正規正交矩陣Q，矩陣長度不變。

證明方式：X拆成向量。旋轉或鏡射，向量長度不變。

X和Q對調依然成立，由於trace的性質。

‖QX‖ꜰ = ‖XQ‖ꜰ = ‖X‖ꜰ when QᵀQ = I

正對角線矩陣D，乘上正規正交矩陣Q，trace變小。

證明方式：D拆成向量。旋轉或鏡射，座標值變小。

極值出現在Q = I，恆等矩陣。

D和Q對調依然成立，由於trace的性質。

tr(QD) = tr(DQ) ≤ tr(D) when QᵀQ = I , D is diagonal , D > 0
(equality holds when Q = I)

tr(QD) = tr(DQ) ≤ tr(D) when QᵀQ = I , D is diagonal , D ≥ 0
(equality holds when QD = D or DQ = D, e.g. Q = I)

範例

仿照(ax - b)²。

minimize ‖AX - B‖ꜰ²              X套用函數之後，跟b的差異盡量小

2Aᵀ(AX - B) = 0                 「一次微分等於零」的地方是極值、鞍點
                                 二次函數、開口向上，必是最小值
AᵀAX = 2AᵀB                      同除以2、展開、移項

X = (AᵀA)⁻¹AᵀB                   normal equation

當X是正規正交矩陣。

minimize ‖AX - B‖ꜰ²   subject to XᵀX = I   正規正交矩陣X套用函數之後，
                                           跟B的差異盡量小
  ‖AX - B‖ꜰ²
= ‖AX‖ꜰ² + ‖B‖ꜰ² - 2 tr((AX)ᵀB)      展開
= ‖AX‖ꜰ² + ‖B‖ꜰ² - 2 tr(XᵀAᵀB)       展開
= ‖A‖ꜰ² + ‖B‖ꜰ² - 2 tr(XᵀAᵀB)        X是正規正交矩陣
= ‖A‖ꜰ² + ‖B‖ꜰ² - 2 tr(XᵀUΣVᵀ)       AᵀB實施奇異值分解
= ‖A‖ꜰ² + ‖B‖ꜰ² - 2 tr(VᵀXᵀUΣ)       cyclic
≥ ‖A‖ꜰ² + ‖B‖ꜰ² - 2 tr(Σ)            Σ是非負對角線矩陣

VᵀXᵀU = I                            極值出現在VᵀXᵀU = I
Xᵀ = VUᵀ                             移項，其中Vᵀ = V⁻¹且Uᵀ = U⁻¹
X = UVᵀ   (AᵀB = UΣVᵀ)               轉置

當X是正規正交矩陣，對調位置。用途是旋轉對齊。

minimize ‖XA - B‖ꜰ²   subject to XᵀX = I
X = UVᵀ   (BAᵀ = UΣVᵀ)

當X是數值。用途是縮放對齊。

minimize ‖xA - B‖ꜰ²     矩陣乘上x倍，跟B的差異盡量小

  ‖xA - B‖ꜰ²
= ‖xA‖ꜰ² + ‖B‖ꜰ² - 2 tr((xA)ᵀB)      展開
= ‖A‖ꜰ² x² + ‖B‖ꜰ² - 2 tr(AᵀB) x     提出
= ‖A‖ꜰ² x² - 2 tr(AᵀB) x + ‖B‖ꜰ²     整理成多項式
= (x - tr(AᵀB) / ‖A‖ꜰ²)² + ......    配方法

x = tr(AᵀB) / ‖A‖ꜰ²

orthogonal Procrustes problem。用途是相似對齊。

s不管多少，最佳R都一樣。因此先求最佳R、再求最佳s。

minimize ‖sRA - B‖ꜰ²   subject to RᵀR = I and s ≥ 0
   s,R                 矩陣A經過旋轉、鏡射、縮放，跟B的差異盡量小

find best R:   (Kabsch–Umeyama algorithm)
  ‖sRA - B‖ꜰ²
= ‖sRA‖ꜰ² + ‖B‖ꜰ² - 2 tr((sRA)ᵀB)    展開
= ‖sRA‖ꜰ² + ‖B‖ꜰ² - 2 tr(sAᵀRᵀB)     展開
= s² ‖RA‖ꜰ² + ‖B‖ꜰ² - 2s tr(AᵀRᵀB)   提出
= s² ‖A‖ꜰ² + ‖B‖ꜰ² - 2s tr(AᵀRᵀB)    R是正規正交矩陣
= s² ‖A‖ꜰ² + ‖B‖ꜰ² - 2s tr(RᵀBAᵀ)    cyclic
= s² ‖A‖ꜰ² + ‖B‖ꜰ² - 2s tr(RᵀUΣVᵀ)   BAᵀ實施奇異值分解
= s² ‖A‖ꜰ² + ‖B‖ꜰ² - 2s tr(VᵀRᵀUΣ)   cyclic
≥ s² ‖A‖ꜰ² + ‖B‖ꜰ² - 2s tr(Σ)        Σ是非負對角線矩陣，且s ≥ 0

VᵀRᵀU = I                            極值出現在VᵀRᵀU = I
Rᵀ = VUᵀ                             移項，其中Vᵀ = V⁻¹且Uᵀ = U⁻¹
R = UVᵀ   (BAᵀ = UΣVᵀ)               轉置

find best s:
  ‖sRA - B‖ꜰ²
≥ s² ‖A‖ꜰ² + ‖B‖ꜰ² - 2s tr(Σ)        極值出現在R = UVᵀ
= ‖A‖ꜰ² s² - 2 tr(Σ) s + ‖B‖ꜰ²       整理成多項式
= (s - tr(Σ) / ‖A‖ꜰ²)² + ......      配方法

s = tr(Σ) / ‖A‖ꜰ²

如果想要去除鏡射，則追加限制條件det(R) = 1。證明過程當中，最小的奇異值再乘上det(R)，讓誤差增加最少。

minimize ‖sRA - B‖ꜰ²   subject to RᵀR = I and s ≥ 0
   s,R                                    and det(R) = 1

D = diag([1 1 ... 1 det(R)])   去除鏡射，奇異值暨奇異向量由大到小排列
R = UDVᵀ                       最小的奇異值再乘上det(R)
s = tr(DΣ)                     最小的奇異值再乘上det(R)

Jacobi's formula

前面提到tr(A)的微分，此處補充det(A)的微分。

                    when A is
∂                   invertable
—— det(A) = adj(A)ᵀ ========== (det(A) A⁻¹)ᵀ = det(A) A⁻ᵀ
∂A