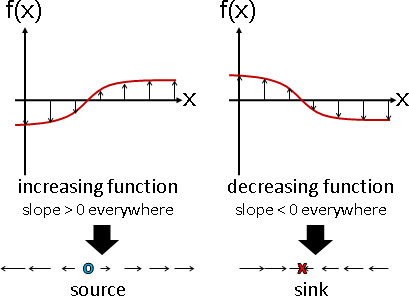
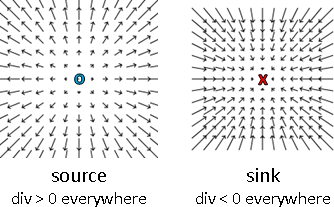
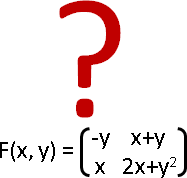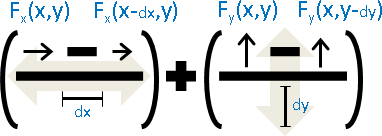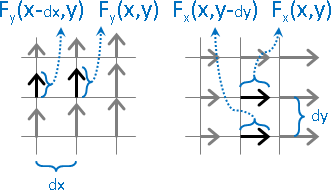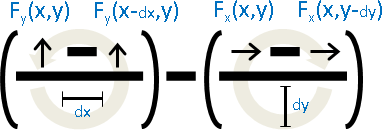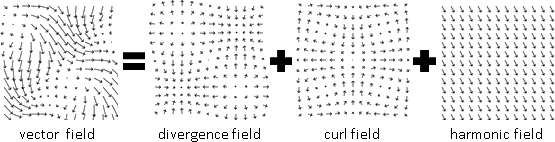multivariate function
多個函數。
⎧ f₁(x, y) = x + y
⎨ f₂(x, y) = 2x² + 1
⎩ f₃(x, y) = 1 / y
數學家重新解讀為:一個函數,輸入與輸出推廣成多個數值。微觀是多個函數,宏觀是一個函數。
F(x, y) = (x + y, 2x² + 1, 1 / y)
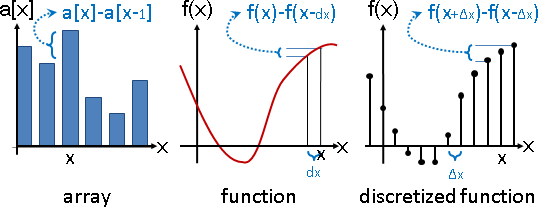
多個數值甚至組成向量、矩陣。多個數值視作一個元件,佯裝成普通的函數。寫來簡便,讀來卻傷腦筋。
⎡ x + y ⎤
F( ⎡ x ⎤ ) = ⎢ 2x² + 1 ⎥
⎣ y ⎦ ⎣ 1 / y ⎦
F(x⃗) = y⃗
原本是「多個函數」,卻被重新解讀,稱作「多變量函數」。
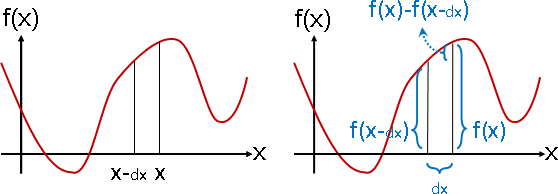
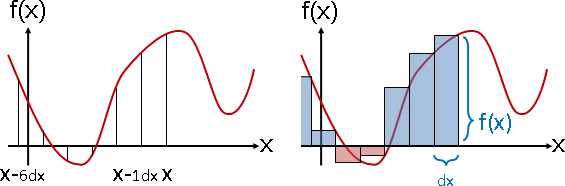
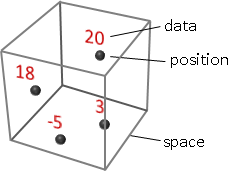
multivariate function可以解讀成「空間處處有數據」
空間處處有數據。(圖例只畫其中幾處。)
空間座標是函數輸入,數據是函數輸出。
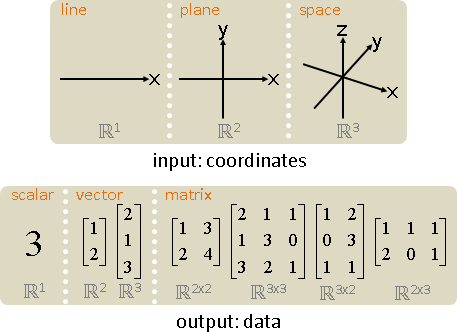
空間可以是一維直線、二維平面、三維空間、……。
數據可以是一個純量(數值)、一個向量、一個矩陣、……。
空間處處有數據,物理學家稱為「場field」。
例如磁場:空間處處有磁力數據。空間是三維空間,數據是一個三維向量。磁力大小是向量長度、磁力方向是向量角度。
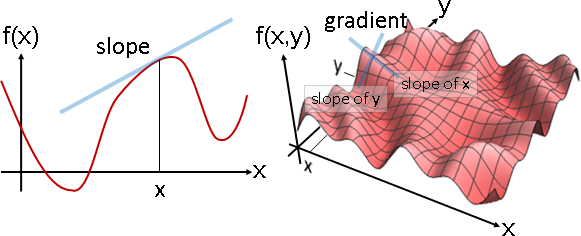
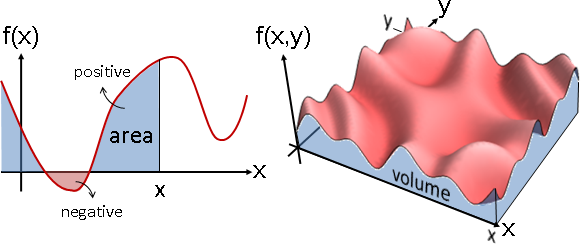
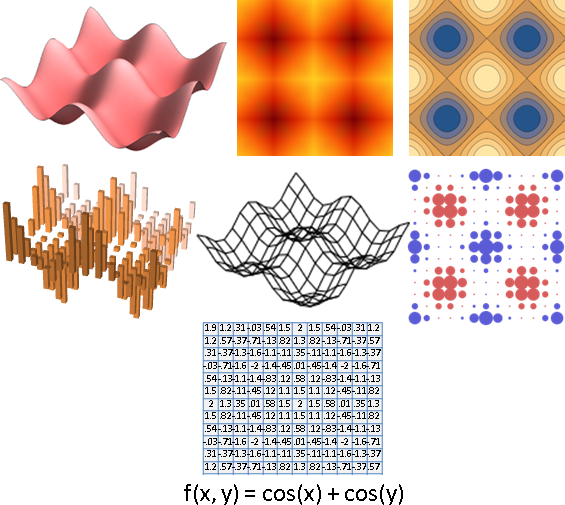
multivariate function可以畫成圖形
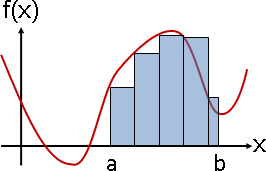
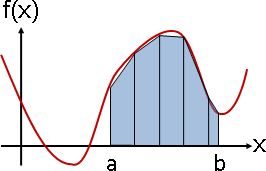
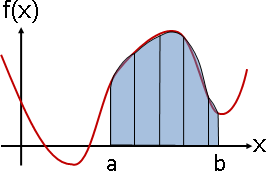
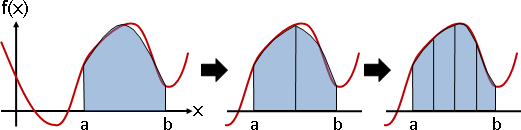
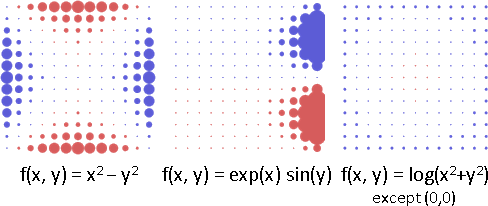
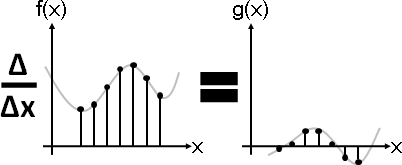
純量場:畫成透視圖、濃度圖、等高線圖。等距取樣之後:畫成長條圖、折線圖、點陣圖、數值陣列。
(圖例是二維空間,省略座標軸。)
Plot3D[Cos[x]+Cos[y], {x, -2Pi, 2Pi}, {y, -2Pi, 2Pi}, Axes -> False, Boxed -> False, Mesh -> None, ColorFunction -> (ColorData["CherryTones"][Rescale[#3, {-2, 2}]] &) ]
DensityPlot[Cos[x]+Cos[y], {x, -2Pi, 2Pi}, {y, -2Pi, 2Pi}, Axes -> False, Frame -> False, MaxRecursion -> 1, PlotPoints -> 5, ColorFunction -> "SolarColors"]
ContourPlot[Cos[x]+Cos[y], {x, -2Pi, 2Pi}, {y, -2Pi, 2Pi}, Axes -> False, Frame -> False]
向量場:畫成軌跡圖 。等距取樣之後:畫成箭矢圖。
VectorPlot3D[{-y, x, 0.5 * z}, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, Boxed -> False, Axes -> False, VectorPoints -> 8, VectorScale -> {Small, Scaled[0.5]}, VectorStyle -> {Black}]
矩陣場:我畫不出來。
分開觀察每個維度,就能勉強畫出來。向量場可以拆成多個純量場。矩陣場可以拆成多個向量場、甚至多個純量場。
multivariate function可以描述世界
物理學家習慣以多變量函數描述物理現象,諸如水流、氣流、熱傳導、電磁場、重力場、聲波、震波、……。精彩的思想突破有:
Faraday 以三維場解釋電磁現象,衍生古典場論。
Einstein 以四維場解釋重力時間現象,衍生相對論。
Schrödinger 以複數四維場解釋波粒現象,衍生量子場論。大家仍在驗證。質量擁有實部虛部,若隱若現,非常奇葩。
想要用計算機模擬物理現象,首先必須瞭解多變量函數!
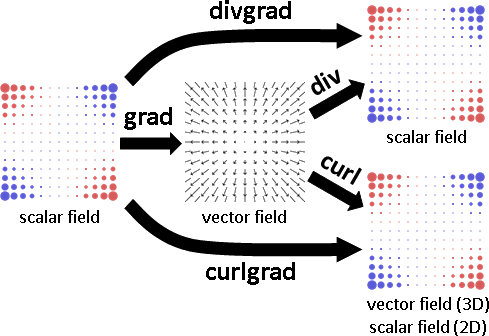
multivariate function運算
除了原本的加減乘除微積,又多了幾種運算:散、旋、梯、梯散、梯旋。數學家並未命名運算名稱,只命名運算結果。
operator result (noun)
---- -------- --------------------------------------------
∇∙ div divergence 散度
∇× curl curl 旋度
∇ grad gradient 梯度
∇∙∇ divgrad Laplacian 梯度的散度(運算符號從右往左疊)
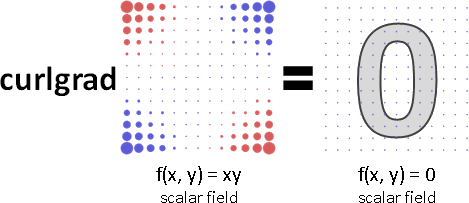
∇×∇ curlgrad --- 梯度的旋度(總是0,缺乏討論意義)
註:∇∙∇經常簡寫成∇²或∆,稱作Laplace運算子。
Laplace運算子(U+2206)、大寫希臘字母delta(U+0394),兩者是相異字元。
然而當今所有字體都沒有特地設計Laplace運算子的造型,
而是直接複製大寫希臘字母delta的造型,導致兩者外觀一模一樣。
https://tex.stackexchange.com/questions/76553/
各種運算如圖所示:
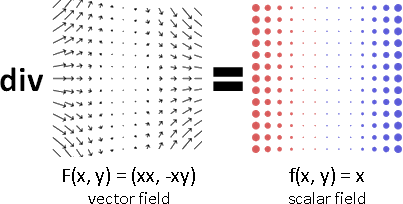
散度
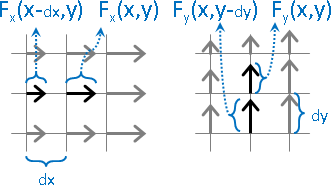
向量場,求散度,得純量場。模仿了點積。
dFx
div(F) = ∇∙F = ——— 1D
dx
∂Fx ∂Fy
div(F) = ∇∙F = ——— + ——— 2D
∂x ∂y
∂Fx ∂Fy ∂Fz
div(F) = ∇∙F = ——— + ——— + ——— 3D
∂x ∂y ∂z
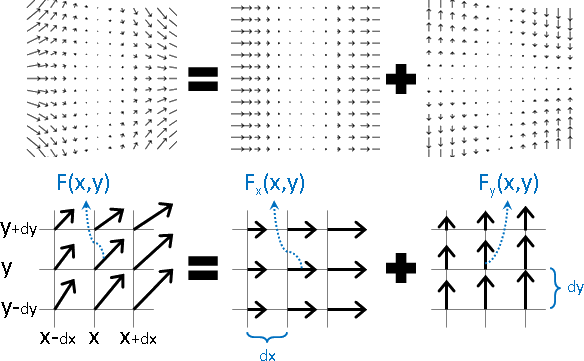
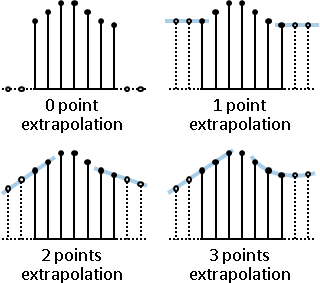
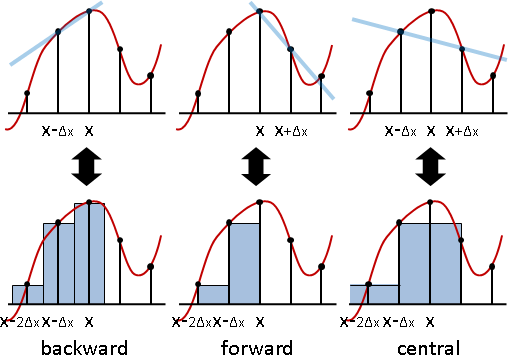
向量場拆成XY兩個分量。觀察座標(x,y)。(三維很難畫,因此圖例為二維。)
X分量的左右差異、Y分量的上下差異,引發了伸縮。
分別除以dx與dy,加總兩個差異。以朝外為正值。
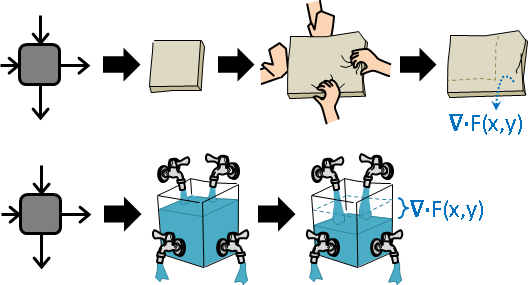
物理意義是每一處的縮放多寡。
實際應用,例如推擠、流動。
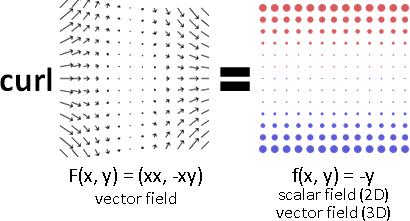
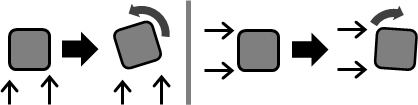
旋度
向量場,求旋度,得向量場。模仿了叉積。
curl(F) = ∇×F = 0 1D
∂Fy ∂Fx ∂Fy ∂Fx
curl(F) = ∇×F = ( 0 , 0 , ——— - ——— ) ==> ——— - ——— 2D
∂x ∂y ∂x ∂y
∂Fz ∂Fy ∂Fx ∂Fz ∂Fy ∂Fx
curl(F) = ∇×F = ( ——— - ——— , ——— - ——— , ——— - ——— ) 3D
∂y ∂z ∂z ∂x ∂x ∂y
Y分量的左右差異、X分量的上下差異,引發了轉動。
分別除以dx與dy,加總兩個差異。以逆時針為正值。
物理意義是每一處的旋轉多寡。
二維旋度是XY平面上的旋轉。三維旋度則是分別於YZ、ZX、XY三個平面上的旋轉。
實際應用,例如渦度。
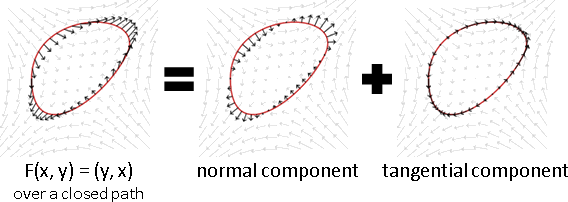
散度定理、旋度定理
任意向量場、任意封閉區域。觀察邊界內、邊界上。
散度定理:邊界內的向量的散度的總和、邊界上的向量的法線分量的總和(通量),兩者相等。
旋度定理:邊界內的向量的旋度的總和、邊界上的向量的切線分量的總和(環量),兩者相等。
原理是(b-a)+(c-b)+(d-c)+...+(z-y) = z-a。導數的區間和=尾項減去頭項。
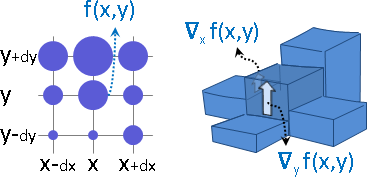
梯度
純量場,求梯度,得向量場。
df
grad(f) = ∇f = —— 1D
dx
∂f ∂f
grad(f) = ∇f = ( —— , —— ) 2D
∂x ∂y
∂f ∂f ∂f
grad(f) = ∇f = ( —— , —— , —— ) 3D
∂x ∂y ∂z
物理意義是相鄰差距。
純量場與梯度向量場,物理學家稱作「勢potential」與「梯度場gradient field」。
例如電勢與電場。電勢的梯度是電場。電勢是一個數值,代表正電荷多寡。正電荷四散,從電勢高往電勢低,形成了電流。空間處處有電流,形成了電場。
梯度的散度【目前稱作Laplace operator】
純量場,先求梯度,再求散度,得純量場。
d²Fx
divgrad(F) = ∆F = ———— 1D
dx²
∂²Fx ∂²Fy
divgrad(F) = ∆F = ———— + ———— 2D
∂x² ∂y²
∂²Fx ∂²Fy ∂²Fz
divgrad(F) = ∆F = ———— + ———— + ———— 3D
∂x² ∂y² ∂z²
物理意義有兩種等價的解釋方式:
一、考慮相鄰差距,差距大小產生對應流量,每一處的瞬間升降多寡,discharge。
二、無視相鄰差距,各處同時均勻四散、離開原處、前往隔壁,每一處的瞬間升降多寡,diffuse。
梯度的旋度
一定是0。不存在樓梯幻覺 。
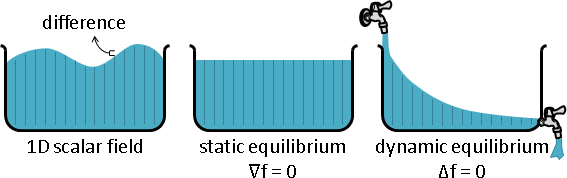
常數函數、和諧函數
常數函數 :相鄰高低差距,處處等於零。數學式子是∇f = 0,梯度處處為零。
換句話說,處處相等。
不生不滅。高者抑之,下者舉之。
和諧函數 :相鄰出入差距,處處等於零。數學式子是∆f = 0,梯度的散度處處為零;梯度的旋度本來就是零。
換句話說,處處等於四周平均。
因果輪迴。萬物並作,吾以觀復。
物理意義是靜態平衡、動態平衡。引入時間變數之後,則是慣性運動、簡諧運動。
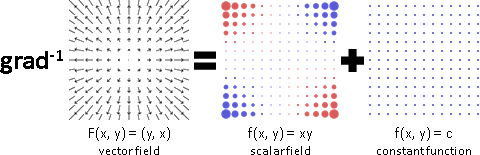
反梯度【有點類似scalar potential】
反梯度有無限多個。常數函數的梯度是零;正解加上任意常數函數,仍是正解。即是「不定積分的常數項」。
反梯度可能不存在。向量場存在樓梯幻覺,就沒有反梯度。
我們可以強行讓反梯度恰好只有一個。針對原本的場,嘗試找到平方誤差最小的場,其存在反梯度。這樣的反梯度,姑且稱作虛擬反梯度,宛如線性代數的虛擬反矩陣。虛擬反梯度的數學公式:散度、反梯散、加上諧勢。請見後面小節散旋諧分解。
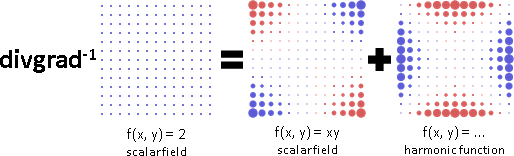
反梯散【目前稱作Poisson equation】
反梯散有無限多個,而且一定存在。和諧函數的梯度的散度是零;正解加上任意和諧函數,仍是正解。
反梯旋【有點類似Clebsch decomposition】
梯度的旋度一定是零。反梯旋似乎缺乏討論意義,查無資料。
Clebsch decomposition有點類似反梯旋,不過我還沒學會。一個向量場等於兩個梯度場的加權總和F=aX+bY,令其中一個權重是常數函數a=1。分解方式無限多種。
F = grad(x) + b grad(y) = X + b Y
整個式子求旋度。原本向量場的旋度,垂直於b與y的梯度。
curl(F) = grad(b) × grad(y)
找到適當的b與y,旋度可以畫成圖形。請參考《Inside Fluids: Clebsch Maps for Visualization and Processing》 。
VIDEO
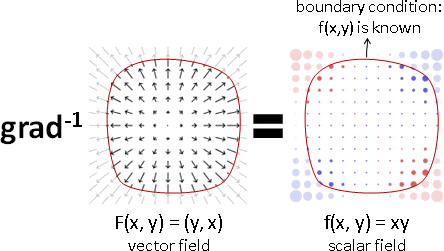
邊界條件:已知函數值
上述的反運算系列,正解都有無限多個。為了有戲可唱,於是數學家追加限制條件,以得到唯一解。
經典的限制條件是邊界條件:指定邊界的輪廓形狀(可以無限寬闊),以及指定邊界的每一個函數值多寡。
電腦做運算,數值要限量。邊界條件派上用場。
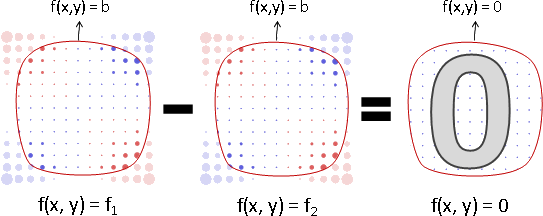
反梯度:任取兩解,相減必為零。沒有相異解,只有唯一解。
已知梯度G,已知反梯度的邊界函數值b,欲求反梯度f。
⎰ grad(f) = G
⎱ bound(f) = b
任取兩解f₁與f₂。
⎰ grad(f₁) = G ⎰ grad(f₂) = G
⎱ bound(f₁) = b ⎱ bound(f₂) = b
兩式相減,抵銷梯度,抵銷邊界。
⎰ grad(f₁) - grad(f₂) = grad(f₁ - f₂) = grad(fdiff ) = 0
⎱ bound(f₁) - bound(f₂) = bound(f₁ - f₂) = bound(fdiff ) = 0
已知梯度0,已知反梯度的邊界函數值0,欲求反梯度fdiff 。
⎰ grad(fdiff ) = 0 梯度是零,即是常數函數。
⎱ bound(fdiff ) = 0 邊界是零,又是常數函數,必然處處是零。
得到fdiff = 0。因此不存在相異解、只存在唯一解。
反梯散:最後一步是和諧函數,處處等於四周平均。若邊界是零,則內部不高於零、不低於零、處處是零。
⎰ graddiv(fdiff ) = 0 梯度的散度是零,即是和諧函數。
⎱ bound(fdiff ) = 0 邊界是零,又是和諧函數,必然處處是零。
反梯度【有點類似scalar potential】
向量場F,當旋度是零∇×F = 0,存在反梯度Φ。
旋度是零∇×F = 0,對於反散度Φ而言即是「梯度的旋度總是零」這條鐵則。
gradient inverse V:
F = ∇V , when ∇×F = ∇×(∇V) = 0
大家將反散度添上負號,稱作「純量位勢scalar potential」。我個人認為添上負號根本是來亂的。
scalar potential Φ:
F = -∇Φ , when ∇×F = ∇×(-∇Φ) = 0
反梯度有無限多個。散度處處為零的場,稱作「無散場solenoidal field」。正解加上任意無散場,仍是正解。
數學證明和數學公式比較複雜。推導過程請見維基百科:
反散度
查無資料。
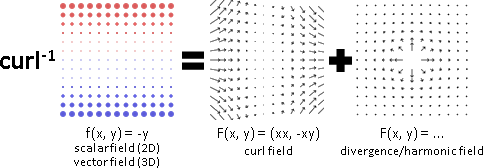
反旋度【目前稱作vector potential】
向量場F,當散度是零∇∙F = 0 ,存在反旋度A,稱作「向量位勢vector potential」。
散度是零∇∙F = 0,對於反旋度A而言即是「旋度的散度總是零」這條鐵則。
vector potential A:
F = ∇×A , when ∇∙F = ∇∙(∇×A) = 0
反旋度有無限多個。旋度處處為零的場,稱作「無旋場irrotational field」。正解加上任意無旋場,仍是正解。
數學證明和數學公式比較複雜。推導過程請見維基百科:
散旋諧分解【目前稱作Helmholtz–Hodge decomposition】
v = (sin(x+y) + 0.5, sin(x-y) - 1)
curl = (sin(x) cos(y), -sin(y) cos(x))
div = (sin(y) cos(x), sin(x) cos(y))
har = (0.5, -1)
div potential = curl potential = sin(x) sin(y)
一個向量場等於三個向量場相加:散場、旋場、諧場。只有唯一一種分解方式。證明省略。
F = D + C + H
such that div(D) ≠ 0, curl(D) = 0,
div(C) = 0, curl(C) ≠ 0,
div(H) = 0, curl(H) = 0
散場:旋度處處是零
旋場:散度處處是零
諧場:兩者處處是零
散場、旋場,處處互相垂直。
諧場,是和諧函數的梯度。
散度、旋度的重要公式:
1. div(grad(f)) = divgrad(f)
2. curl(grad(f)) = 0
3. curl(curl(F)) = grad(div(F)) - div(grad(F))
4. div(curl(F)) = 0
註:向量場F的梯度的散度:Fx Fy Fz三個純量場各自求梯度的散度。
散場公式、旋場公式,用到其中兩道公式。
為了排除諧勢,用來計算旋場的公式引入Coulomb gauge。
用來計算散場的公式:
div(grad(f)) = divgrad(f)
用來計算旋場的公式:
⎰ curl(curl(F)) = grad(div(F)) - div(grad(F))
⎱ div(F) = 0 Coulomb gauge
div(grad(f)) = divgrad(f) curl(curl(F)) = - div(grad(F))
grad div curl curl
散勢 ───→ 散場 ───→ 散度 旋勢 ───→ 旋場 ───→ 旋度
(純量場) (向量場) (純量場) (向量場) (向量場) (向量場)
│ ↑ │ ↑
╰──────────────────╯ ╰──────────────────╯
divgrad -divgrad
散場公式、旋場公式,為了排除諧場,只好繞一大圈。
以散場公式為例:一、求散度,以排除諧場,畢竟諧場的散度是零。也排除旋場,畢竟旋場的散度是零。二、求反梯散,得到散勢。三、求梯度,得到散場。
div curl
場 ───→ 散度 場 ───→ 旋度
┊DCH │equal ┊DCH │equal
grad ⇣ ↓ curl ⇣ ↓
散勢 ───→ 散場 散度 旋勢 ───→ 旋場 旋度
(純量場) (向量場) (純量場) (向量場) (向量場) (向量場)
↑ │ ↑ │
╰──────────────────╯ ╰──────────────────╯
divgrad⁻¹ -divgrad⁻¹
(Poisson equation) (Poisson equation)
⎧ D = grad(divgrad⁻¹(div(F)))
⎨ C = curl(-divgrad⁻¹(curl(F)))
⎩ H = F - D - C
註:令邊界函數值為零,確保divgrad⁻¹有唯一解、不含和諧函數。
散場:求散度、求反梯散、求梯度
旋場:求旋度、三個值分別求反梯散、三個值變號、求旋度
旋場(二維):求旋度(只得z值)、求反梯散、變號、求梯度、轉90度
諧場:減散場、減旋場
散勢加諧勢,即是虛擬反梯度。
散場加諧場,即是平方誤差最小的梯度場。宛如投影。
原本的場,平方誤差最小的梯度場,兩者散度一樣。
div curl
場 ───→ 散度 場 ───→ 旋度
proj┊ │equal proj┊ │equal
grad ⇣ div ↓ curl ⇣ curl ↓
散勢 ───→ 散場 ───→ 散度 旋勢 ───→ 旋場 ───→ 旋度
+諧勢 +諧場 +零 +諧勢 +諧場 +零
諧場隨意分攤給散場、旋場,稱作Helmholtz decomposition。散場摻加諧場,形成無旋場。旋場摻加剩下的諧場,形成無散場。
F = Dirr + Csole
F = grad(dirr ) + grad(csole )
散旋諧分解,也有人寫成勢的風格,而非場的風格。
F = D + C + H = grad(d) + curl(c) + grad(h)
⎧ d = grad⁻¹(D) = divgrad⁻¹(div(F))
⎨ c = curl⁻¹(C) = -divgrad⁻¹(curl(F))
⎩ h = grad⁻¹(H)
散勢:散場的反梯度
旋勢:旋場的反旋度
旋勢(二維):旋場轉-90度的反梯度
諧勢:諧場的反梯度
散旋諧分解的傅立葉轉換,我還沒有學會。
縱場:散場的傅立葉轉換
橫場:旋場的傅立葉轉換
查無資料:諧場的傅立葉轉換
http://physics.stackexchange.com/questions/1115/