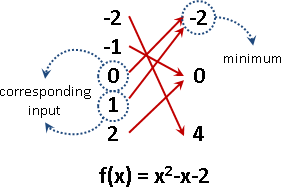
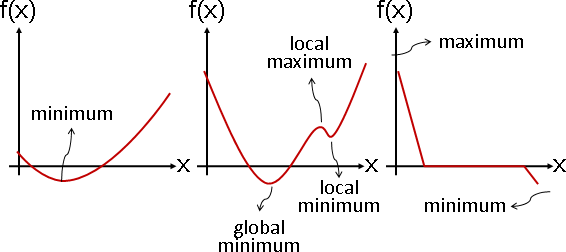
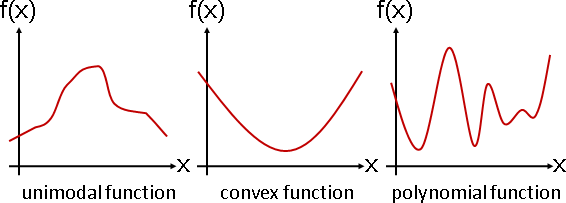
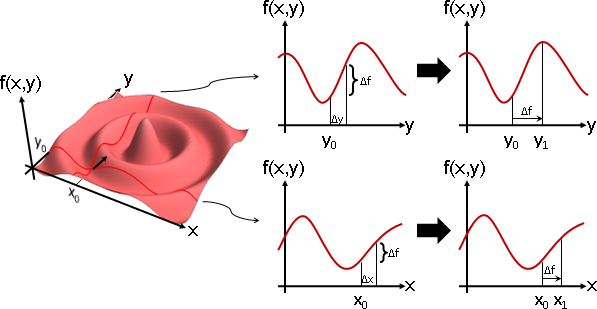
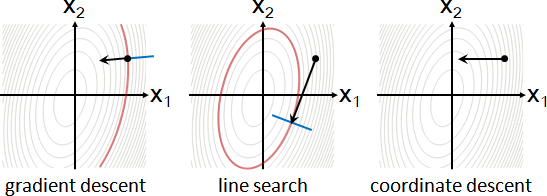
constrained optimization
「約束最佳化」。最佳化，限制輸入範圍。
輸入只能是受規範的、被指定的數值。
maximize f(x)
x ∈ C
「約束最佳化」。最佳化、等式與不等式組，兩者合體。
輸入必須同時滿足許多道等式與不等式。
maximize f(x) subject to g(x) = 0, h(x) ≥ 0, ...
約束最佳化當中，函數稱作「目標函數objective function」。等式與不等式組稱作「約束條件constraint」。等式與不等式可以重新整理成函數的模樣，稱作「約束函數constraint function」。
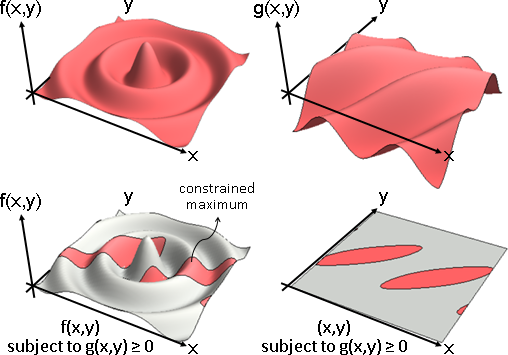
通常會存在太過完美的輸入，所以只好抑制。
施加限制，以求得更對味的答案。
Show[
Plot3D[(Cos[(x-y)/2 - 3] + Cos[y/4])/2 - 1/2, {x, -4Pi, 4Pi}, {y, -4Pi, 4Pi}, PlotRange -> {-1, 1}, Boxed -> False, Mesh -> None, Axes -> False, PlotPoints -> 50, ColorFunction -> (ColorData["CherryTones"][Rescale[#3, {-4, 4}]] &)],
ParametricPlot3D[{{u,-4Pi,0}, {-4Pi,u,0}}, {u, -4Pi, 4Pi}, PlotStyle -> {Black, Black}]
]
Show[
Plot3D[BesselJ[0, Norm[{x, y}]], {x, -4Pi, 4Pi}, {y, -4Pi, 4Pi}, PlotRange -> {-1, 1}, Boxed -> False, Mesh -> None, Axes -> False, PlotPoints -> 50, ColorFunction -> (ColorData["GrayTones"][Rescale[#3, {-6, 2}]] &)],
Plot3D[BesselJ[0, Norm[{x, y}]] + 0.01, {x, -4Pi, 4Pi}, {y, -4Pi, 4Pi}, PlotRange -> {-1, 1}, Boxed -> False, Mesh -> None, Axes -> False, PlotPoints -> 50, RegionFunction -> Function[{x, y, z}, Cos[(x-y)/2 - 3] + Cos[y/4] > 1], ColorFunction -> (ColorData["CherryTones"][Rescale[#3, {-4, 4}]] &)]
]
Show[
Plot3D[0, {x, -4Pi, 4Pi}, {y, -4Pi, 4Pi}, PlotRange -> {-1, 1}, Boxed -> False, Mesh -> None, Axes -> False, PlotPoints -> 50, ColorFunction -> (ColorData["GrayTones"][Rescale[#3, {-6, 2}]] &)],
Plot3D[0.01, {x, -4Pi, 4Pi}, {y, -4Pi, 4Pi}, PlotRange -> {-1, 1}, Boxed -> False, Mesh -> None, Axes -> False, PlotPoints -> 50, RegionFunction -> Function[{x, y, z}, Cos[(x-y)/2 - 3] + Cos[y/4] > 1], ColorFunction -> (ColorData["CherryTones"][Rescale[#3, {-4, 4}]] &)]
]
ContourPlot[(Cos[(x-y)/2 - 3] + Cos[y/4])/2 - 1/2 == 0, {x, -4Pi, 4Pi}, {y, -4Pi, 4Pi}]
conditional gradient method（條件梯度法）
feasible direction method（可行方向法）
梯度下降法改良版。總是朝向約束條件。
p = argmin [ ∇f(x) dot (p - x) ] = argmin [ ∇f(x) dot p ]
p∈C p∈C
xnext = x + step ⋅ (p - x)
從約束條件當中，找出最符合當前梯度方向、最靠近當前位置的地點（以點積大小來判斷），然後朝該地點走一步。
找到該地點，是另一個最佳化問題。兩層最佳化。
如果約束函數很單純，則推導公式解，得到該地點。如果約束函數很複雜，則以梯度下降法，找到該地點。
projected gradient method（投影梯度法）
梯度下降法改良版。每當偏離約束條件，立即歸位。
p = x + step ⋅ ∇f(x)
xnext = argmin ‖ p - xnext ‖
xnext∈C
朝著梯度方向走一步，然後立即垂直投影到約束條件上面。換句話說，若離開約束條件，則走最短直線抵達約束條件；若未離開約束條件，則維持現狀。
垂直投影，是另一個最佳化問題。兩層最佳化。
如果約束函數很單純，則推導垂直投影公式，一步到位。如果約束函數很複雜，則以梯度下降法慢慢走入約束條件：約束函數的梯度方向，權且作為垂直投影方向。
Lagrange multiplier（拉格朗日乘數）
當約束條件是等式，約束最佳化可以化作微分方程組求解。
f(x,y) 求極值。必須滿足 g(x,y) = 0。
湊出 L(x,y,λ) = f(x,y) + λ g(x,y)。
f(x,y) 的極值，等同 L(x,y,λ) = f(x,y) + λ g(x,y) 的極值。
欲求極值：
對 x 偏微分，讓斜率是 0。
對 y 偏微分，讓斜率是 0。
不管 λ 如何變化，λ g(x,y) 都是零，L(x,y,λ) 永遠不變。
欲求永遠不變的地方：
對 λ 偏微分，讓斜率是 0。
三道偏微分方程式聯立，其解涵蓋了（不全是）所有符合約束條件的極值。
⎧ ∂/∂x L(x,y,λ) = 0
⎨ ∂/∂y L(x,y,λ) = 0
⎩ ∂/∂λ L(x,y,λ) = 0
上述微分方程組，簡寫成「梯度等於零」、「求駐點」。
∇L(x,y,λ) = 0
L(x,y,λ)稱作「拉格朗日函數Lagrangian」。λ稱作「拉格朗日乘數Lagrange multiplier」。
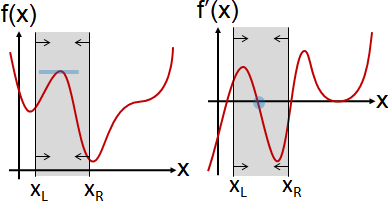
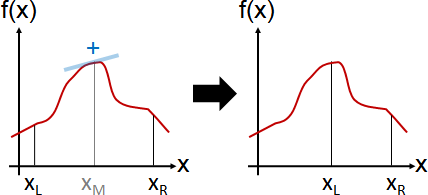
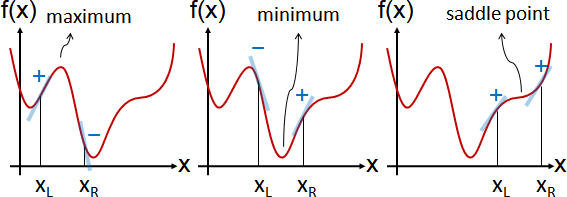
微分方程組的解（拉格朗日函數的駐點），涵蓋所有正確答案，卻也可能包含錯誤答案。必須驗證答案。檢查每個答案的鄰近函數值（篩去鞍點）、比較每個答案的函數值（篩去局部極值）。
∇L(x,y,λ) = 0 梯度等於零、求駐點。
max L(x,y,λ) ✘ 注意到，求駐點，不等價於求極值。
x,y,λ
max min L(x,y,λ) ✘ 注意到，求駐點，不等價於求鞍點。
x,y λ
另外還可以進一步得到非常漂亮的數學性質：極值所在之處，目標函數與約束函數，兩者梯度方向共線，而梯度大小不明。（梯度大小設定成未知倍率λ。）
三式分別偏微分。
⎧ ∂/∂x L(x,y,λ) = 0
⎨ ∂/∂y L(x,y,λ) = 0
⎩ ∂/∂λ L(x,y,λ) = 0
展開L(x,y,λ) = f(x,y) + λ g(x,y)。
偏微分是線性函數，擁有分配律。
⎧ ∂/∂x f(x,y) + λ ⋅ ∂/∂x g(x,y) = 0
⎨ ∂/∂y f(x,y) + λ ⋅ ∂/∂y g(x,y) = 0
⎩ g(x,y) = 0
第一式、第二式合起來，簡寫成梯度，並且重新整理。
∇f(x,y) + λ ∇g(x,y) = 0
∇f(x,y) = -λ ∇g(x,y)
拉格朗日函數改為L(x,y,λ) = f(x,y) - λ g(x,y)。
改變正負號，式子比較帥。
∇f(x,y) = λ ∇g(x,y)
上述微分方程組，簡寫成「梯度比例」。
⎰ ∇f(x,y) = λ ∇g(x,y)
⎱ g(x,y) = 0
當約束條件是大量等式，則通通乘上倍率再加總。
f(x,y) 求極值。必須滿足 g₁(x,y) = 0 與 g₂(x,y) = 0 與……。
定義 L(x,y,λ₁,λ₂,...) = f(x,y) + λ₁ g₁(x,y) + λ₂ g₂(x,y) + ...
Karush–Kuhn–Tucker conditions（KKT條件）
約束條件是等式：稱作拉格朗日乘數。極值位於約束條件上面。
極值所在之處，目標函數與約束函數，兩者梯度方向共線，而梯度大小不明。（梯度大小設定成未知倍率λ。）
maximize f(x) subject to g(x) = 0
---> solve ⎰ ∇f(x) = λ ∇g(x)
⎱ g(x) = 0
約束條件是不等式：稱作KKT條件。極值可能位於約束條件邊界或者內部。
邊界：目標函數與約束函數，兩者梯度方向共線，而梯度大小不明。（梯度大小設定成未知倍率μ。）
內部：目標函數的極值位置，已經滿足約束條件。約束條件無關緊要。（μ設定成零，讓約束條件失效。）
計算學家將兩種情況分開處理，邊界是微分方程組求解，內部是目標函數最佳化。數學家則是將兩種情況合併成一個方程組。
maximize f(x) subject to h(x) ≥ 0
---> solve ⎧ ∇f(x) = μ ∇h(x)
⎨ μ ≤ 0
⎩ h(x) ≥ 0
極值位於約束條件邊界時，梯度方向的判斷方式：
一、最大值位於邊界：目標函數的梯度方向，離開邊界。
二、約束函數大於等於零：約束函數的梯度方向，進入邊界。
梯度方向恰好相反，梯度大小必須異號。（μ必須小於零。）
| ∇f(x) = μ ∇h(x) | ∇f(x) + μ ∇h(x) = 0
----------------------|-----------------|---------------------
max f(x) st h(x) ≥ 0 | μ ≤ 0 | μ ≥ 0
max f(x) st h(x) ≤ 0 | μ ≥ 0 | μ ≤ 0
min f(x) st h(x) ≥ 0 | μ ≥ 0 | μ ≤ 0
min f(x) st h(x) ≤ 0 | μ ≤ 0 | μ ≥ 0
約束條件是大量等式與不等式：各有倍率，通通加總。
maximize f(x) subject to g₁(x) = 0, g₂(x) = 0, h₁(x) ≥ 0, h₂(x) ≥ 0
---> solve ⎧ ∇f(x) = λ₁ ∇g₁(x) + λ₂ ∇g₂(x) + μ₁ ∇h₁(x) + μ₂ ∇h₂(x)
⎪ g₁(x) = 0
⎪ g₂(x) = 0
⎨ μ₁ ≤ 0
⎪ h₁(x) ≥ 0
⎪ μ₂ ≤ 0
⎩ h₂(x) ≥ 0
penalty method（懲罰法）
約束函數取平方、自訂倍率，摻入目標函數。
maximize f(x) subject to g(x) = 0
---> maximize f(x) subject to g(x) = 0 and ρ/2 g(x)² = 0
---> maximize f(x) + ρ/2 g(x)² subject to g(x) = 0
函數變陡，梯度下降法更快找到極值，不易停在鞍點。
大家習慣讓倍率除以二，配合二次方。微分時，係數相消。
barrier method（屏障法）
約束函數取對數、自訂倍率、視情況變號，摻入目標函數。
minimize f(x) subject to h(x) ≥ 0
---> minimize f(x) subject to h(x) ≥ 0 and
-ρ log(h(x)) ≥ ∞ and ρ ≥ 0
---> minimize f(x) - ρ log(h(x)) subject to h(x) ≥ 0 and ρ ≥ 0
邊界附近，函數趨近正無限大，梯度下降法不易出界。
alternating direction method of multipliers（交替方向乘數法）
一、懲罰法：約束函數取平方，摻入目標函數。（可用可不用）
二、拉格朗日乘數：約束最佳化化作函數求駐點。
三、座標下降法：變數求極值，走到最高處；乘數偏微分求根，朝梯度方向走一步。
當前位置在約束條件內與外，梯度方向正與負。【尚待確認】
非負乘數，利用投影梯度法，利用max(μ,0)保持非負。
maximize f(x) subject to g(x) = 0, h(x) ≥ 0
L(x,λ,μ) = f(x) + λ g(x) + μ h(x) where μ ≥ 0
xnext = argmax { f(x) + λ g(x) + μ h(x) }
λnext = λ + step ⋅ g(x)
μnext = max(μ + step ⋅ h(x), 0)
範例：限制條件是多道一次不等式，併成一個一次方程組。
maximize f(x) subject to Ax ≤ b
L(x,μ) = f(x) + μᵀ (Ax - b) where μ ≤ 0
xnext = argmax { f(x) + μᵀ (Ax - b) }
μnext = min(μ + step ⋅ (Ax - b), 0)
範例：兩個函數相加。使用了懲罰法。
minimize f(x) + g(y) subject to Ax + By = c
L(x,y,λ) = f(x) + g(y) + λᵀ (Ax + By - c) + (ρ/2) ‖Ax + By - c‖²
xnext = argmin L(x,y,λ)
ynext = argmin L(x,y,λ)
λnext = λ + step ⋅ (Ax + By - c)
interior point method（內點法）
一、屏障法：約束函數取對數，摻入目標函數。（可用可不用）
二、拉格朗日乘數：約束最佳化化作微分方程組。
三、牛頓法：多變數函數求根。
