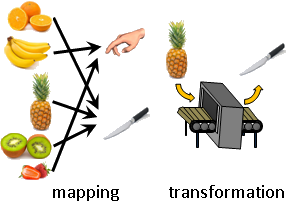
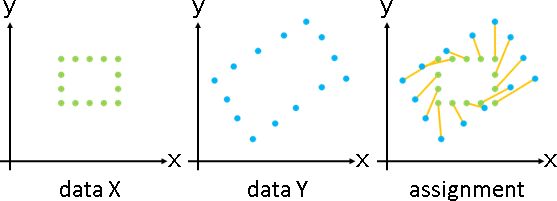
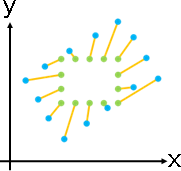
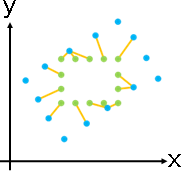
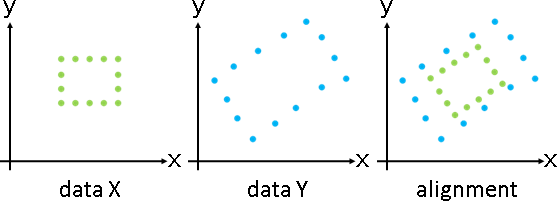
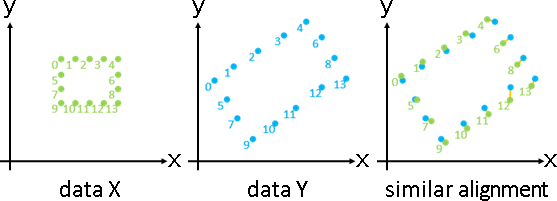
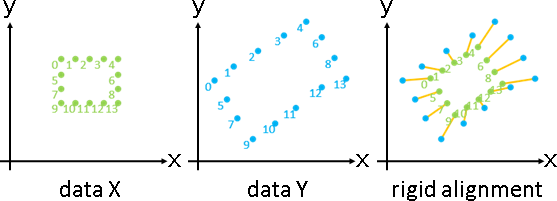
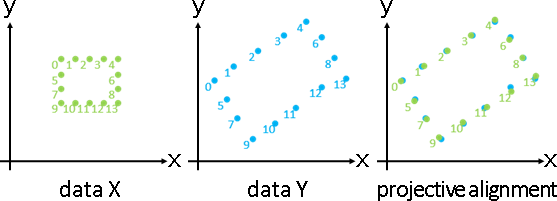
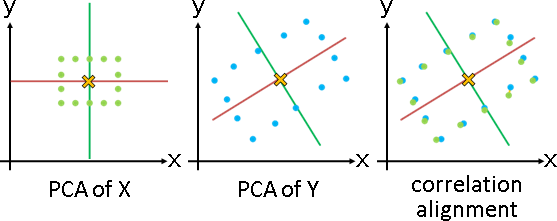
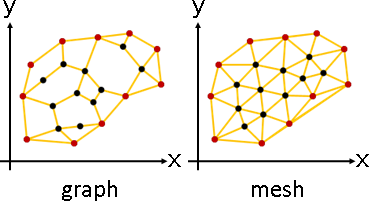
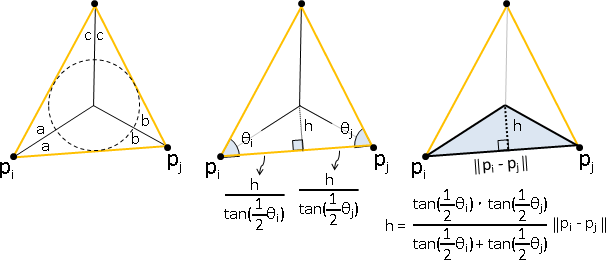
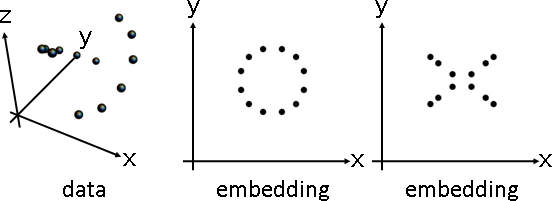
deformation(topology-preserving transformation)
「形變」。調整數據,盡量保持原始造型。
「形變」。已知甲堆數據,求得乙堆數據、變換函數。
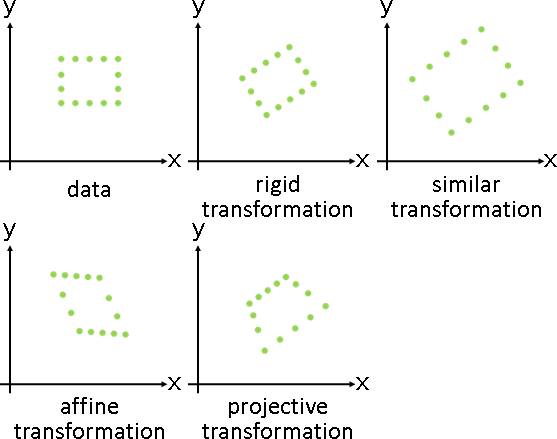
採用全域變換,造型死板無法微調,於是大家採用局部變換。
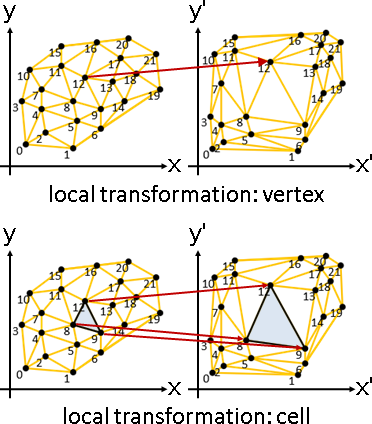
圖的局部變換:
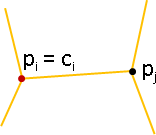
點變換:各點擁有變換函數。
p̕ᵢ = Fᵢ(pᵢ)
網格擁有面,多了一種方式:
面變換:各面擁有變換函數,作用於頂點。
p̕ᵢ = Fc(pᵢ) for i∈cell(c)
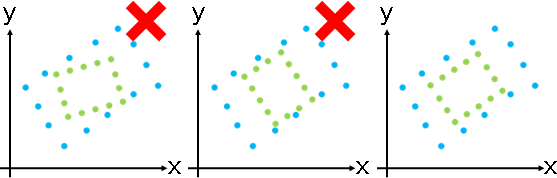
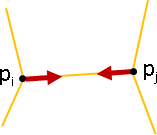
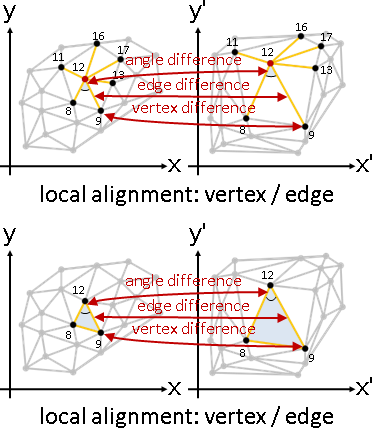
圖的局部對齊:
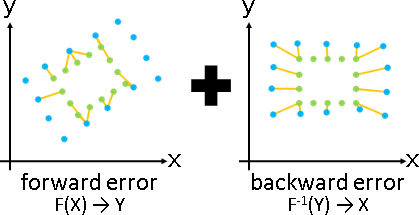
點變換、點誤差:各點擁有變換函數。自身與鄰點實施變換,統計各點差異。
min sum { ‖p̕ᵢ - Fᵢ(pᵢ)‖² + sum ‖p̕ⱼ - Fᵢ(pⱼ)‖² }
F,p̕ i j∈adj(i)
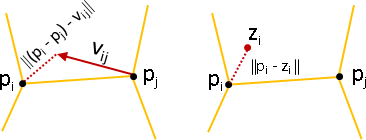
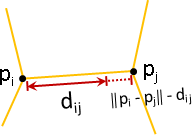
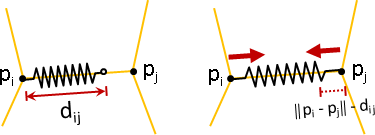
點變換、邊誤差:各點擁有變換函數。自身與鄰點實施變換,統計各邊(向量)差異。
min sum sum ‖(p̕ᵢ - p̕ⱼ) - (Fᵢ(pᵢ) - Fᵢ(pⱼ))‖²
F,p̕ i j∈adj(i)
點變換、角誤差:各點擁有變換函數。自身與鄰點實施變換,統計各角差異。
min sum sum ‖θ̕ⱼ - Fᵢ(θⱼ)‖²
F,p̕ i j∈adj(i)
where θ̕ⱼ = ∠p̕ⱼp̕ᵢp̕ⱼ₊₁
Fᵢ(θⱼ) = ∠Fᵢ(pⱼ)Fᵢ(pᵢ)Fᵢ(pⱼ₊₁)
網格擁有面,多了三種方式:
面變換、點誤差:各面擁有變換函數。頂點實施變換,統計各點差異。
min sum sum ‖p̕ᵢ - Fc(pᵢ)‖²
F,p̕ c i∈cell(c)
面變換、邊誤差:各面擁有變換函數。頂點實施變換,統計各邊(向量)差異。
min sum sum ‖(p̕ᵢ - p̕ⱼ) - (Fc(pᵢ) - Fc(pⱼ))‖²
F,p̕ c (i,j)∈cell(c)
面變換、角誤差:各點擁有變換函數。頂點實施變換,統計各角差異。
min sum sum ‖θ̕ᵢ - Fc(θᵢ)‖²
F,p̕ c i∈cell(c)
where θ̕ᵢ = ∠p̕ᵢ₋₁p̕ᵢp̕ᵢ₊₁
Fc(θᵢ) = ∠Fc(pᵢ₋₁)Fc(pᵢ)Fc(pᵢ₊₁)
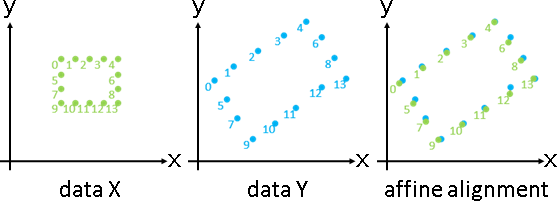
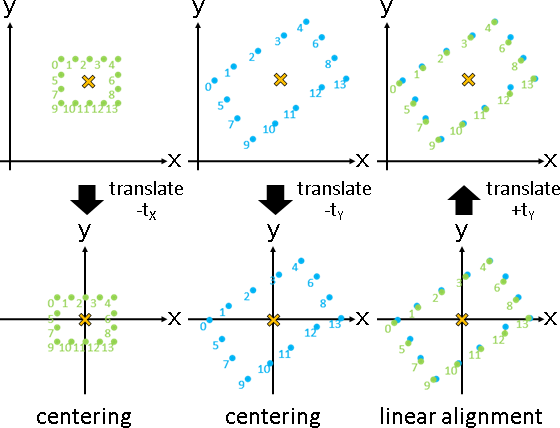
affine deformation
點變換、點誤差。
min sum { ‖p̕ᵢ - (Aᵢ(pᵢ) + b)‖² + sum ‖p̕ⱼ - (Aᵢ(pⱼ) + b)‖² }
F,p̕ i j∈adj(i)
保留局部造型,鄰角一齊變化,角度大小穩定。
演算法是大型稀疏矩陣、一次最小平方方程組、公式解。
點仿射變換,邊無法疊合。邊重新畫上即可。
《Laplacian Surface Editing》
affine deformation
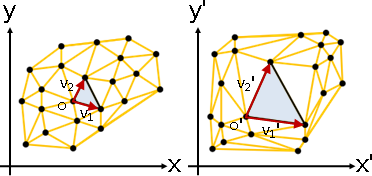
面變換、點誤差。
min sum sum ‖p̕ᵢ - (Ac(pᵢ) + b)‖²
F,p̕ c i∈cell(c)
可以完全對齊,毫無誤差。三角形任選一點作為原點,其兩鄰邊作為基底。
solve A(pᵢ - t) = (p̕ᵢ - t̕) for i = 1,2,3
solve A(pᵢ - p₁) = (p̕ᵢ - p̕₁) for i = 2,3
⎡ | | ⎤ ⎡ | | ⎤
V = ⎢ p₂-p₁ p₃-p₁ ⎥ V̕ = ⎢ p̕₂-p̕₁ p̕₃-p̕₁ ⎥
⎣ | | ⎦ ⎣ | | ⎦
AV = V̕
A = V̕V⁻¹
不會維持形狀,缺乏討論意義。
laplacian preserving deformation
恆等變換(點面無區別)、邊誤差。
min sum wᵢⱼ ‖(p̕ᵢ - p̕ⱼ) - (pᵢ - pⱼ)‖²
p̕ (i,j)
效果是盡量保持形狀。附帶效果是相對距離盡量均勻。
改寫成二次型、一次方程組。恰是「圖論版本的保梯散變換」!
min (x̕-x)ᵀL(x̕-x) + min (y̕-y)ᵀL(y̕-y) where pᵢ = (xᵢ, yᵢ)
x̕ y̕ p̕ᵢ = (x̕ᵢ, y̕ᵢ)
solve Lx̕ = Lx and solve Ly̕ = Ly
演算法請參考先前章節:相對距離盡量均勻。
答案是直接複製貼上,缺乏討論意義。大家習慣追加其他限制條件,例如某些點位置必須固定。
solve L₀₀x̕ = L₀₀x - L₀₁c and solve L₀₀y̕ = L₀₀y - L₀₁d
rigid deformation / similar deformation
點變換、邊誤差。
min sum sum ‖(p̕ᵢ - p̕ⱼ) - Rᵢ(pᵢ - pⱼ)‖²
R,p̕ i j∈adj(i)
演算法是分塊座標下降法:固定p̕求得R、固定R求得p̕,不斷輪流。rigid alignment與Laplacian preserving deformation不斷輪流。
固定p̕求得R:(pᵢ - pⱼ)和(p̕ᵢ - p̕ⱼ)視作點,化作rigid alignment。公式解。
鄰點們的平均數是定值。預先中心化,以便快速求解。
YXᵀ = UΣVᵀ
R = UVᵀ
固定R求得p̕:Rᵢ(pᵢ - pⱼ) = (Rᵢpᵢ - Rᵢpⱼ)視作兩點相減,化作Laplacian preserving deformation。矩陣求解。
Laplacian matrix是定值。預先做Cholesky decomposition,以便快速求解。
solve Lx̕ = Lx
solve MMᵀx̕ = Lx where L = MMᵀ
點剛體變換,邊無法疊合。最後得到類似剛體的變換。不是剛體變換,不是盡量剛體變換(奇異值與1的平方誤差總和盡量小)。
《As-Rigid-As-Possible Surface Modeling》
rigid deformation / similar deformation
面變換、邊誤差。
min sum sum ‖(p̕ᵢ - p̕ⱼ) - Rc(pᵢ - pⱼ)‖²
R,p̕ c (i,j)∈cell(c)
演算法是分塊座標下降法。
固定p̕求得R:化作三個點的rigid alignment。
固定R求得p̕:無法化作Laplacian preserving deformation,原始論文搞錯了。正確方法請參考先前章節:相對位置盡量固定。
面剛體變換,面無法接合。分塊座標下降法最後一步不能停在rigid alignment。
最後得到類似剛體的變換。不是剛體變換,不是盡量剛體變換。
時間複雜度較高,缺乏討論意義。
《A Local/Global Approach to Mesh Parameterization》
isotropic scaling deformation
面變換、邊誤差。
min sum sum ‖(p̕ᵢ - p̕ⱼ) - sc(pᵢ - pⱼ)‖²
s,p̕ c (i,j)∈cell(c)
演算法是分塊座標下降法。
固定p̕求得s:簡易公式解,不必奇異值分解。
固定s求得p̕:同先前小節。
min sum sum ‖(p̕ᵢ - p̕ⱼ) - sc(pᵢ - pⱼ)‖²
s c (i,j)∈cell(c)
solve sum sum { 2 (p̕ᵢ - p̕ⱼ)ᵀ(pᵢ - pⱼ) - 2 sc ‖pᵢ - pⱼ‖² } = 0
c (i,j)∈cell(c)
sc = [ sum (p̕ᵢ - p̕ⱼ)ᵀ(pᵢ - pⱼ) ] ÷ [ sum ‖pᵢ - pⱼ‖² ]
(i,j)∈cell(c) (i,j)∈cell(c)
不允許旋轉,只允許縮放,三角形容易交疊。額外拿向量長度做regularization,維持局部造型,避免交疊。
...... + sum sum ‖(p̕ᵢ - p̕ⱼ) - lᵢⱼ(pᵢ - pⱼ)‖²
c (i,j)∈cell(c)
where lᵢⱼ = ‖p̕ᵢ - p̕ⱼ‖ ÷ ‖pᵢ - pⱼ‖
演算法是分塊座標下降法:固定p̕求得s和l、固定s和l求得p̕,不斷輪流。
為了方便求解,原始論文偷吃步,固定l求得p̕。然而l包含p̕,不能拆開計算。只好改拿上一步的向量長度做regularization。
...... + sum sum ‖(p̕ᵢ⁽ᵗ⁾ - p̕ⱼ⁽ᵗ⁾) - lᵢⱼ(pᵢ - pⱼ)‖²
c (i,j)∈cell(c)
where lᵢⱼ = ‖p̕ᵢ⁽ᵗ⁻¹⁾ - p̕ⱼ⁽ᵗ⁻¹⁾‖ ÷ ‖pᵢ - pⱼ‖
自我審查之後,就可以使用分塊座標下降法了。工程精神!
《Optimized Scale-and-Stretch for Image Resizing》
isogonal affine deformation
面變換、角誤差。
min sum { ‖θ̕₁ - θ₁‖² + ‖θ̕₂ - θ₂‖² + ‖θ̕₃ - θ₃‖² }
θ̕ c
⎧ θ̕₁ + θ̕₂ + θ̕₃ = π , ∀c 三角形內角和180°
⎪
⎪ sum { θ̕₁ } = 2π , ∀c 鄰角和360°
⎪ c∈adj(i)
subject to ⎨
⎪ prod { sin(θ̕₂) ÷ sin(θ̕₃) } = 1 , ∀c
⎪ c∈adj(i) 鄰邊長度比,繞一圈為1
⎪
⎩ θ̕₁, θ̕₂, θ̕₃ ≥ 0 , ∀c 角度非負
一旦確定角度,也就決定網格(可能鏡射)。因此直接求角度。
二次規劃。演算法是牛頓拉格朗日乘數法。
直接拷貝,就是保角,缺乏討論意義。因此大家討論其他情況,例如重新釘住某些點,例如三維表面變成二維平面。
《ABF++: Fast and Robust Angle Based Flattening》
isogonal affine deformation
網格的變換,可以用經典數學領域來詮釋:微積分的分段變換(連續雙射)、圖論的局部變換(面變換)。微積分考慮所有地點,圖論僅考慮點與邊。
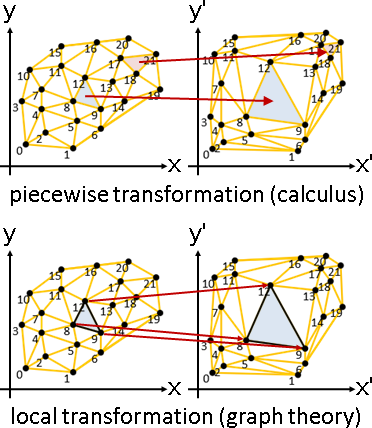
網格的仿射變換,擁有許多特殊性質:
一、輸入輸出劃定網格,各三角形各自實施仿射變換。
二、輸入輸出劃定網格,只有唯一一種仿射變換。
三、微積分分段仿射=圖論局部仿射。
註:三角形處處做仿射變換=三頂點做仿射變換+內部做仿射座標系。
四、微積分保長≠圖論保長。註:圖論保長未定義。
五、微積分保距≠圖論保距。
六、微積分保角=圖論保角。
七、微積分和諧≠圖論和諧。
八、微積分保角≠微積分和諧。
九、當面積固定,微積分盡量保角=微積分盡量和諧。
十、微積分能量=圖論能量(使用Lcot)。
第十項,能量是指Dirichlet energy。證明如下:
微積分能量:處處梯度平方和。用於函數。用於區域。
圖論能量:兩兩距離平方和。用於圖。用於點與邊。
∫ ‖∇F‖ꜰ² 微積分能量
= sum ∫c ‖∇Fc‖ꜰ² 分段變換
c
= sum area(c) ‖Acᵀ‖ꜰ² 分段仿射變換 p̕ = Ap + b
c
= either [DDG2016 at TU Berlin] or [Pinkall93]
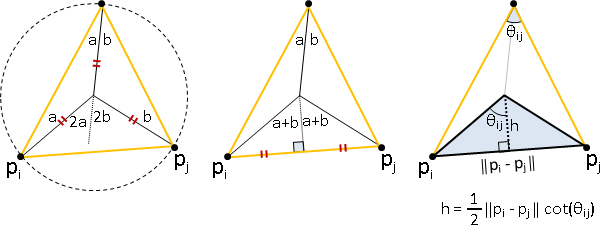
= sum sum ¼ cot(θᵢⱼ) ‖p̕ᵢ - p̕ⱼ‖² 原網格的夾角
c (i,j)∈cell(c) 新網格的邊長
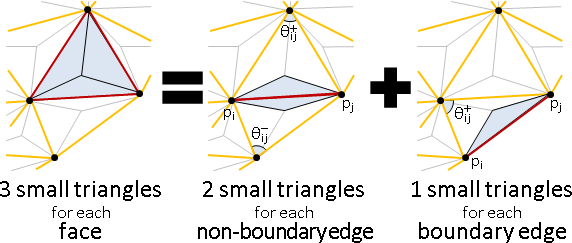
= sum (¼ cot(θᵢⱼ⁺) + ¼ cot(θᵢⱼ⁻)) ‖p̕ᵢ - p̕ⱼ‖² 主角從面變邊
(i,j) ^^^^^^^^^^^^^^^^^^^^^^^^^^^
wᵢⱼ
= x̕ᵀLcotx̕ + y̕ᵀLcoty̕ 主角從邊變點,圖論能量
宛如外心面積公式Lcot。不知是否能換成內心面積公式Ltan。
總結:當面積固定,圖論盡量保角=微積分盡量保角=微積分盡量和諧=微積分能量盡量小=圖論能量盡量小(使用Lcot)。
min x̕ᵀLcotx̕ + min y̕ᵀLcoty̕ where p̕ᵢ = (x̕ᵢ, y̕ᵢ)
x y
solve Lcotx̕ = 0 and solve Lcoty̕ = 0
問題得以化作先前章節:面積盡量均勻。沿用原網格的夾角。
令新網格邊界是凸多邊形,釘住網格邊界,以保證面積固定。
令原網格是Delaunay triangulation,以保證除了邊界以外的wᵢⱼ非負,以保證L₀₀有反矩陣、有唯一解。
《Spectral Conformal Parameterization》
凸包性質(mean value property)
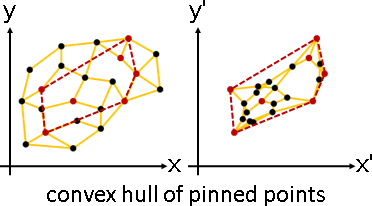
graph Laplacian analysis精髓:各點更新為鄰點的加權平均。
GLA不允許負權重。因此各點位於鄰點的凸包內部。
釘住某些點,形變之後,所有點都將位於釘點的凸包內部。
平面圖性質(Tutte's spring theorem)
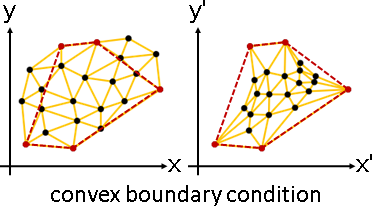
僅適用網格。
當釘點們形成凸多邊形,網格形變之後仍是網格。所有點不會超出凸多邊形,所有邊不會交叉,所有角不會翻面。
當釘點們形成凸多邊形,而且位於網格邊界,網格形變之後不會退化。點邊角不會疊合在一起。
當釘點們形成凹多邊形,網格形變之後可能是網格、可能不是網格。表面積公式有可能失效。
對稱正定性質(Rippa's theorem)
能量盡量小(使用Lcot)、最小角盡量大,兩者密切相關。
給邊求點(釘住邊界上所有點、補滿邊界上所有邊):
可以採用Dirichlet energy minimization (Lcot)。
恰好形成Delaunay triangulation。
給點求邊:
可以採用Delaunay triangulation。
恰好形成Dirichlet energy minimization (Lcot)。
最小角盡量大=兩個相鄰三角形的共用邊不可翻轉=對頂角的cot值總和非負。
Delaunay triangulation iff wᵢⱼ = ¼ cot(θᵢⱼ⁺) + ¼ cot(θᵢⱼ⁻) ≥ 0
where (i,j) is not boundary
Delaunay triangulation可能有鈍角,但是保證wᵢⱼ非負(不含邊界),進而保證L₀₀是對稱正定矩陣(釘住邊界)。
《A Spectral Characterization of the Delaunay Triangulation》
minimum energy deformation
(minimal surface of membrane ⇒ Laplacian)
smoothing energy: min sum ‖J(Fc)‖ꜰ² ⇒ solve Lcotx = 0
F c
(minimal curvature of thin plate ⇒ bilaplacian)
bending energy: min sum ‖H(Fc)‖ꜰ² ⇒ solve Lcot²x = 0
F c
J(F) = ∇Fᵀ 最近似線性變換矩陣
‖J(F)‖² 能量
min ‖J(F)‖² 盡量和諧
變換函數的一次微分的長度盡量小,化作一階梯散方程式求解。
物理意義:面積盡量小。盡量拉緊。適用於薄膜,例如肥皂泡。
變換函數的二次微分的長度盡量小,化作二階梯散方程式求解。
物理意義:曲率盡量小。盡量壓平。適用於薄片,例如厚紙板。
次方越高,形狀越圓。
《Polygon Mesh Processing》
rigid deformation / similar deformation
rigid energy: min sum ‖Rc - J(Fc)‖ꜰ²
F,R c
similar energy: min sum ‖Sc - J(Fc)‖ꜰ²
F,S c
方才的數學式子,追加特定變換函數,形成了剛體、相似。
如果已知F,那麼R和S有公式解。R和S改寫成F的形式之後,未知數只剩下F。
目前沒有演算法。大家沿用之前的演算法,矩陣改成Lcot。
isometric energy: min sum { area(c) [(σ₁ - 1)² + (σ₂ - 1)²] }
F,σ c
isogonal energy: min sum { area(c) (σ₁ - σ₂)² }
F,σ c
順帶一提,有人將數學式子改寫成奇異值的形式。奇異值是絕對值,省略了正負號,包含了鏡射,形成了保距、保角。
《Variational Harmonic Maps for Space Deformation》
boundary-free deformation
不釘住邊界,而是自由調整邊界,讓網格更加均勻。
min Ed(M,M̕) + λ₁ Eb(B) + λ₂ Ed(S,S̕)
Ed(.,.) = sum ‖J(Fc)‖ꜰ² + ‖J(Fc⁻¹)‖ꜰ²
c
Eb(.) = sum sum max(0, ε / dᵢⱼₖ - 1)²
(i,j) k≠i,j
dᵢⱼₖ = ‖pᵢ - pₖ‖ + ‖pⱼ - pₖ‖ - ‖pᵢ - pⱼ‖ triangle inequality
λ₁ λ₂ ε are positive constants
不釘住邊界,讓邊界盡量保持相同,方法是追加最佳化目標。
一、網格M,能量盡量小(對稱方式)。
二、邊界B,鄰點距離盡量小、非鄰點距離盡量大。
三、邊界包覆一層薄薄的網格S,能量盡量小(對稱方式)。
《Efficient Bijective Parameterizations》
equiareal affine deformation
目前沒有演算法。這裡介紹一個大概差不多的演算法。
能量=變換矩陣元素平方和=奇異值平方和=縮放倍率平方和。
一個頂點的平均能量sᵢ:相鄰三角形的能量的加權平均數。權重是面積。
sᵢ = sum { area(c) ‖Ac‖² } ÷ sum { area(c) }
c∈adj(i) c∈adj(i)
平均能量sⱼ,開根號,當作邊長縮放率sqrt(sⱼ)。
邊長縮放率取倒數當作權重。權重越大,距離越短。
min sum wᵢⱼ ‖p̕ᵢ - p̕ⱼ‖² where wᵢⱼ = 1 / sqrt(sⱼ)
每個想法乍看合情合理,但是沒有數學證明。論文聲稱的盡量不伸縮也只是推測。
演算法是分塊座標下降法:固定q求得A、固定A求得q,不斷輪流。
《A Fast and Simple Stretch-Minimizing Mesh Parameterization》
備忘:gradient-Laplacian deformation
目前沒有論文、也沒有實際用處。
我們希望指定數據造型。我們設計一個複雜的最佳化目標函數:梯度差異(邊)、梯散差異(點:鄰邊和),平方總和盡量小。
min { sum ‖(pᵢ-pⱼ) - (p̕ᵢ-p̕ⱼ)‖² + sum ‖sum (pᵢ-pⱼ) - sum (p̕ᵢ-p̕ⱼ)‖² }
p̕ (i,j) i j∈adj(i) j∈adj(i)
~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~
gradient diff (edge diff) Laplacian diff (vertex diff)
改寫成向量。
min { sum ‖vᵢⱼ - v̕ᵢⱼ‖² + sum ‖sum vᵢⱼ - sum v̕ᵢⱼ‖² }
p̕ (i,j) i j∈adj(i) j∈adj(i)
where vᵢⱼ = pᵢ - pⱼ , v̕ᵢⱼ = p̕ᵢ - p̕ⱼ
每個維度可以分開處理,分開最佳化。
引入adjacency matrix,改寫成矩陣運算。
vᵢⱼ的x座標,視作矩陣Aₓ。vᵢⱼ的y座標,視作矩陣A。
min { ‖Aₓ - A̕ₓ‖ꜰ² + ‖Dₓ - D̕ₓ‖ꜰ² }
x̕
+ min { ‖A - A̕‖ꜰ² + ‖D - D̕‖ꜰ² } where p̕ᵢ = (x̕ᵢ, y̕ᵢ)
y̕
引入Laplacian matrix,合併A與D。
A沒有對角線,D只有對角線。
min ‖Lₓ - L̕ₓ‖ꜰ² + min ‖L - L̕‖ꜰ² where p̕ᵢ = (x̕ᵢ, y̕ᵢ)
x̕ y̕
演算法是梯度下降法。每一步皆以當前的x̕求得L̕ₓ。
gradient are 2(L̕ₓ - Lₓ)𝟏 and 2(L̕ - L)𝟏
答案是直接拷貝,缺乏討論意義。大家習慣讓vᵢⱼ是任意非負對稱矩陣,不必是兩兩相減。大家也習慣追加其他限制條件。