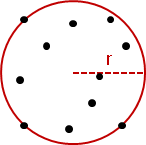
minimum enclosing rectangle

二維平面的矩形，包圍所有點。可令面積最小、令周長最小。

凸包，旋轉卡尺。O(NlogN)。

UVa 819 10173 ICPC 5138

UVa 12307

minimum enclosing box / minimum bounding box

三維空間的長方體，包圍所有點，體積最小。

三維旋轉卡尺？正確性不明。O(N³)。

UVa 12308

maximum empty rectangle

Largest Empty Rectangle among a Point Set. Jeet Chaudhuri, Subhas C. Nandy. 1999.

O(N³)。

maximum empty axis-parallel rectangle

二維平面的矩形，不含任何點，矩形擺正，面積最大。

平面邊界四個角落補點，窮舉每一點當作矩形左（與右）邊界，然後依序掃描右方（與左方）的點作為右（左）邊界，掃描過程中隨時更新上下邊界。另外，矩形的左右邊界可能是平面的左右邊界。O(N²)。

divide-and-conquer method。O(Nlog³N)。

UVa 10043

minimum enclosing square annulus

二維平面的方環，包圍所有點。可令寬度最小、令面積最小。

ICPC 6121

maximum weight axis-aligned rectangle

二維平面上有許多點，每個點有權重，有正有負。找到一個擺正的矩形，內部所有點的權重總和最大。

O(N²)。

minimum enclosing circle

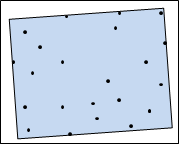
二維平面的圓，包圍所有點，面積暨周長暨半徑最小。

一個圓包圍所有點，半徑相對伸縮後，一個點歸屬所有圓。

【待補圖片】

最佳化。coordinate descent改良版。O(Nlog²R)。

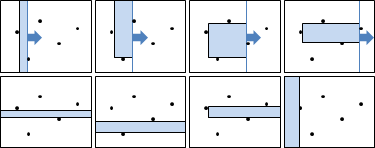
固定參數，問題簡化為圓心X座標未知、Y座標已知。觀察每種X座標的半徑，恰是單峰函數（谷形）。Y座標微調，仍是單峰函數。未知已知對調，仍是單峰函數。兩者皆未知，形成二維單峰函數。兩層trisection method，X座標逐步走到最低處，Y座標總是走到最低處。求X座標O(logR)回合，求Y座標O(logR)回合，每回合枚舉所有點以求得半徑。總時間複雜度O(Nlog²R)。

圓心位於farthest point Voronoi diagram頂點。O(NlogN)。

randomized incremental method。平均O(N)，最差O(N²)。

以遞增法求最小包圍圓，逐次添加一點，並且調整最小包圍圓。若新點在圓內，不做任何事；若新點在圓外，則新點一定在新圓上，但是本來的點就不一定在新圓上了。於是得到新問題：已知一點在圓上，求最小包圍圓。接著又得到新問題：已知兩點在圓上，求最小包圍圓。已知兩點時，以枚舉法掃描所有點，找到最遠的點。

添加一點的時間複雜度分成兩種情況：圓不變、圓變動。因為無法預測變動，所以窮舉各種結果、反推變動機率。各種結果是新圓上有兩點、有三點。現有i點、已知一點在圓上，因此新點導致新圓的機率是(2-1)/i、(3-1)/i。添加一點的平均時間複雜度是O(1)，添加N點的平均時間複雜度是O(N)。原始問題以此類推，平均時間複雜度O(N)。

UVa 10005 11681

minimum enclosing ball / minimum bounding sphere

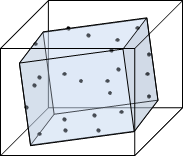
三維空間的球，包圍所有點，體積暨表面積暨半徑最小。

最佳化。coordinate descent改良版。O(Nlog³R)。

Welzl's algorithm。平均O(N)。

UVa 10095

minimum k enclosing circle

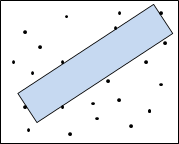
二維平面的圓，包圍k個點，面積暨周長暨半徑最小。

order k Voronoi diagram。O(NlogN + k²N)。

二元搜尋半徑r。窮舉每個點，作為圓邊界，顯然圓心與該點相距r。旋轉的掃描線，圓繞該點一圈。O(logR ⋅ N ⋅ NlogN)。

承上，只取鄰點來掃描，以該點為中心，取正方形邊長4r之內所有點，確保點數低於k(16r²)/(πr²) < 5.1k。range tree。O(logR ⋅ N ⋅ (klogk + log²N))。

ICPC 7488

maximum empty circle / maximum inscribed circle

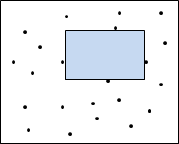
二維平面的圓，不含所有點和邊，面積暨周長暨半徑最大。

一群點最大空圓：圓心位於Voronoi diagram的頂點上。如果平面有邊界，那麼圓心也可能在邊上。O(NlogN)。

凸多邊形最大內切圓：每條邊同時往垂直方向等速內縮。每條邊配合左右鄰邊的角平分線，就可求得消失所需距離。換個觀點，不內縮了，改為預測最快消失的邊，刪除此邊，左右鄰邊延長銜接於一點，就縮小問題範疇了。所有邊放入二元樹，按照消失順序排序，每當刪除一條邊就更新二元樹。O(NlogN)。

凸多邊形最大內切圓：二元搜尋內切圓半徑，以半平面交集驗證。O(NlogR)。

UVa 11257 ICPC 3890

簡單多邊形最大內接圓。【待補文字】

正交多邊形最大內接圓。【待補文字】

ICPC 2994

minimum enclosing annulus

二維平面的環，內圍外圍圓心相同，包圍所有點。可令寬度最小、令面積最小。

建立Voronoi diagram與farthest point Voronoi diagram，窮舉三種情況。O(N²)。

一外三內：窮舉外點；窮舉圓心，即Voronoi diagram的點。O(N²)。
兩外兩內：窮舉Voronoi diagram的邊，
　　　　　窮舉farthest point Voronoi diagram的邊，
　　　　　兩邊求交點，作為圓心。O(N²)。
三外一內：窮舉內點；窮舉圓心，即farthest point Voronoi diagram的點。O(N²)。

maximum empty annulus

minimum enclosing triangle

二維平面的三角形，包圍所有點。可令面積最小、令周長最小。

maximum empty triangle

二維平面的三角形，不含任何點，面積最大。

當平面沒有邊界，這個問題沒有討論意義；把三角形壓扁、拉長，即不含任何點、面積無限大。

如果設定了三角形的角度範圍，那麼就有討論意義了。

如果給定的平面擁有一個長方形邊界，然後多邊形是凸的呢？
這個時候就不會有面積無限大的多邊形了吧？

不是凸的形狀，就只能採用「頂點屬於給定的點集合」。
若是凸的形狀（如三角形、長方形、凸多邊形、圓形），
除了可以採用「頂點屬於給定的點集合」，
也可以採用「邊界碰到給定的點集合」。

這種時候就不知道如何命名了。

UVa 10112

minimum enclosing convex polygon = convex hull

凸多邊形，包圍所有點，面積暨周長最小。

即「convex hull」。

maximum empty convex polygon
（largest empty convex subset）

凸多邊形，不含任何點，一群點挑幾個點作為頂點。可令頂點最多、令面積最大、令周長最大。

頂點最多：點線對偶，掃描線。O(N³)。

minimum enclosing convex k-gon

凸k邊形，包圍所有點，可令面積最小、令周長最小。

extremum empty convex k-gon
（largest empty convex subset）

凸k邊形，不含任何點，一群點挑k個點作為頂點，可判斷是否存在、令面積最小最大、令周長最小最大。

判斷是否存在：NP-hard。

面積周長最小最大：O(kN³)。

面積周長最大：O((kN + NlogN) ⋅ logN)。運用「SMAWK algorithm」得加速到O(kN + NlogN)。

ICPC 2674

extremum convex k-gon

凸k邊形，一群點挑k個點作為頂點。可判斷是否存在、令面積最小最大、周長最小最大。

判斷是否存在，即「Erdős–Szekeres conjecture」。

演算法同上。

extremum convex hull of k points

凸多邊形，邊界暨內部恰有k個點。可判斷是否存在、令面積最小最大、周長最小最大。

演算法同上。

minimum simple polygon

簡單多邊形，所有點作為頂點，可令面積最小、令邊長最小。

NP-hard。

UVa 12386

longest segment in simple polygon

簡單多邊形，內部最長線段。

最長線段：必然碰到其中兩個頂點，否則可以旋轉線段變得更長。窮舉兩頂點，計算線段與多邊形交點。O(N³)。

最長對角線：O(N(logN)³)。

ICPC 4756

maximum convex polygon in simple polygon
（potato peeling）

簡單多邊形，內部最大凸多邊形。把凹凹凸凸削平。

O(N⁷)。