dynamic programming

先透過一個簡單的例子，感受一下「動態規劃」吧！

範例：階乘（factorial）

1 × 2 × 3 × ⋯ × N。整數1到N的連乘積。N階乘。N!。

N!源自(N-1)!，如此就遞迴分割問題了。

陣列的每一格對應每一個問題。設定第一格的答案，再以迴圈依序計算其餘答案。

const int N = 10; int f[N]; void factorial() { f[0] = 0; f[1] = 1; for (int i=2; i<=N; ++i) f[i] = f[i-1] * i; } const int N = 10; void factorial() { int f = 1; for (int i=2; i<=N; ++i) f *= i; }

UVa 623 568 10220 10323

時間複雜度

總共N個問題，每個問題花費O(1)時間，總共花費O(N)時間。

空間複雜度

求1!到N!：總共N個問題，用一條N格陣列儲存全部問題的答案，空間複雜度O(N)。

只求N!：用一個變數累計乘積，空間複雜度O(1)。

dynamic programming
= divide-and-conquer method + memoization

動態規劃是分治法的延伸。當分治法分割出來的問題，一而再、再而三出現，就運用記憶法儲存這些問題的答案，避免重複求解，以空間換取時間。

動態規劃的過程，就是反覆地讀取數據、計算數據、儲存數據。

1. 把原問題遞迴分割成許多更小的問題。（recurrence）
   1-1. 子問題與原問題的求解方式皆類似。（optimal sub-structure）
   1-2. 子問題會一而再、再而三的出現。（overlapping sub-problems）
2. 設計計算過程：
   2-1. 確認每個問題需要哪些子問題來計算答案。（recurrence）
   2-2. 確認總共有哪些問題。（state space）
   2-3. 把問題一一對應到表格。（lookup table）
   2-4. 決定問題的計算順序。（computational sequence）
   2-5. 確認初始值、計算範圍。（initial states / boundary）
3. 實作，主要有兩種方式：
   3-1. top-down
   3-2. bottom-up

1. recurrence

遞迴分割問題時，當子問題與原問題完全相同，只有數值範圍不同，我們稱此現象為recurrence，再度出現、一再出現之意。

【註：recursion和recurrence，中文都翻譯為「遞迴」，然而兩者意義大不相同，讀者切莫混淆。】

此處以爬樓梯問題當作範例。先前於遞歸法章節，已經談過如何求踏法，而此處要談如何求踏法數目。

踏上第五階，只能從第四階或從第三階踏過去。因此「爬到五階」源自兩個子問題：「爬到四階」與「爬到三階」。

「爬到五階」的踏法數目，就是總合「爬到四階」與「爬到三階」的踏法數目。寫成數學式子是「f(5) = f(4) + f(3)」，其中「f(‧)」表示「爬到某階之踏法數目」。

依樣畫葫蘆，得到「f(4) = f(3) + f(2)」、「f(3) = f(2) + f(1)」。

「爬到兩階」與「爬到一階」無法再分割、沒有子問題，直接得到「f(2) = 2」、「f(1) = 1」。

整理成一道簡明扼要的遞迴公式：

f(n) =
 ⎧ 1                , if n = 1
 ⎨ 2                , if n = 2
 ⎩ f(n-1) + f(n-2)  , if n >= 3 and n <= 5

爬到任何一階的踏法數目，都可以藉由這道遞迴公式求得。n代入實際數值，遞迴計算即可。

為什麼分割問題之後，就容易計算答案呢？因為分割問題時，同時也分類了這個問題的所有可能答案。分類使得答案的規律變得單純，於是更容易求得答案。

2-1. recurrence

f(n) =
 ⎧ 1                , if n = 1
 ⎨ 2                , if n = 2
 ⎩ f(n-1) + f(n-2)  , if n >= 3

2-2. state space

想要計算第五階的踏法數目。

全部的問題是「爬到一階」、「爬到二階」、「爬到三階」、「爬到四階」、「爬到五階」。

至於「爬到零階」、「爬到負一階」、「爬到負二階」以及「爬到六階」、「爬到七階」沒有必要計算。

2-3. lookup table

建立六格的陣列，儲存五個問題的答案。

表格的第零格不使用，第一格是「爬到一階」的答案，第二格是「爬到二階」的答案，以此類推。

如果只計算「爬完五階」，也可以建立三個變數交替使用。

2-4. computational sequence

因為每個問題都依賴「階數少一階」、「階數少二階」這兩個問題，所以必須由階數小的問題開始計算。

計算順序是「爬到一階」、「爬到二階」、……、「爬到五階」。

2-5. initial states / boundary

最先計算的問題是「爬到一階」與「爬到二階」，必須預先將答案填入表格、寫入程式碼，才能繼續計算其他問題。心算求得「爬到一階」的答案是1，「爬到二階」的答案是2。

最後計算的問題是原問題「爬到五階」。

為了讓表格更順暢、為了讓程式碼更漂亮，可以加入「爬到零階」的答案，對應到表格的第零格。「爬到零階」的答案，可以運用「爬到一階」的答案與「爬到兩階」的答案，刻意逆推而得。

最後可以把初始值、尚待計算的部份、不需計算的部分，統整成一道遞迴公式：

f(n) =
 ⎧ 0                , if n < 0               [exterior]
 ⎪ 1                , if n = 0               [initial state]
 ⎨ 1                , if n = 1               [initial state]
 ⎪ f(n-1) + f(n-2)  , if n >= 2 and n <= 5   [computation]
 ⎩ 0                , if n > 5               [exterior]

UVa 11069

3. 實作

直接用遞迴實作，而不使用記憶體儲存各個問題的答案，是最直接的方式，也是最慢的方式。時間複雜度O(f(n))。問題一而再、再而三的出現，不斷呼叫同樣的函式求解，效率不彰。剛接觸DP的新手常犯這種錯誤。

int f(int n) { if (n == 0 || n == 1) return 1; else return f(n-1) + f(n-2); }

正確的DP，是一邊計算，一邊將計算出來的數值存入表格，以後便不必重算。這裡整理了兩種實作方式，各有優缺點：

1. top-down
2. bottom-up

3-1. top-down

int table[6]; // 表格，儲存全部問題的答案。 bool solve[6]; // 記錄問題是否已經計算完畢 int f(int n) { // [initial states] if (n == 0 || n == 1) return table[n] = 1; // [computation] // 如果已經計算過，就直接讀取表格的答案。 if (solve[n]) return table[n]; // 如果不曾計算過，就計算一遍，儲存答案。 table[n] = f(n-1) + f(n-2); // 將答案存入表格 solve[n] = true; // 已經計算完畢 return table[n]; } void stairs_climbing() { for (int i=0; i<=5; i++) solve[i] = false; int n; while (cin >> n && (n >= 0 && n <= 5)) cout << "爬到" << n << "階，" << f(n) << "種踏法"; } int table[6]; // 合併solve跟table，簡化程式碼。 int f(int n) { // [initial states] if (n == 0 || n == 1) return 1; // [computation] // 用 0 代表該問題還未計算答案 // if (table[n] != 0) return table[n]; if (table[n]) return table[n]; return table[n] = f(n-1) + f(n-2); } void stairs_climbing() { for (int i=0; i<=5; i++) table[i] = 0; int n; while (cin >> n && (n >= 0 && n <= 5)) cout << "爬到" << n << "階，" << f(n) << "種踏法"; }

這個實作方式的好處是不必斤斤計較計算順序，因為程式碼中的遞迴結構會迫使最小的問題先被計算。這個實作方式的另一個好處是只計算必要的問題，而不必計算所有可能的問題。

這個實作方式的壞處是程式碼採用遞迴結構，不斷呼叫函式，執行效率較差。這個實作方式的另一個壞處是無法自由地控制計算順序，因而無法妥善運用記憶體，浪費了可回收再利用的記憶體。

UVa 10285 10446 10520

3-2. bottom-up

訂定一個計算順序，然後由最小的問題開始計算。特色是程式碼通常只有幾個迴圈。這個實作方式的好處與壞處，與前一個方式恰好互補。

首先建立表格。

int table[6]; int table[5 + 1];

心算「爬到零階」的答案、「爬到一階」的答案，填入表格當中，作為初始值。分別填到表格的第零格、第一格。

table[0] = 1; table[1] = 1;

尚待計算的部份就是「爬到兩階」的答案、……、「爬到五階」的答案。通常是使用迴圈，按照計算順序來計算。

計算過程的實作方式，有兩種迥異的風格。一種是「往回取值」，常見的實作方式。

int table[6]; void dynamic_programming() { // [initial states] table[0] = 1; table[1] = 1; // [computation] for (int i=2; i<=5; i++) table[i] = table[i-1] + table[i-2]; }

另一種是「往後補值」，罕見的實作方式。

int table[6]; void dynamic_programming() { // [initial states] for (int i=0; i<=5; i++) table[i] = 0; table[0] = 1; // table[1] = 1; // 剛好可以被算到 // [computation] for (int i=0; i<=5; i++) { if (i+1 <= 5) table[i+1] += table[i]; if (i+2 <= 5) table[i+2] += table[i]; } }

計算完畢之後，最後印出答案。

void stairs_climbing() { dynamic_programming(); int n; while (cin >> n && (n >= 0 && n <= 5)) cout << "爬到" << n << "階，" << table[n] << "種踏法"; }

UVa 495 900 10334

總結

第一。先找到原問題和其子問題們之間的關係，寫出遞迴公式。如此一來，便可利用遞迴公式，用子子問題的答案，求出子問題的答案；用子問題的答案，求出原問題的答案。

第二。確認可能出現的問題全部總共有哪些，這樣才能知道要計算哪些問題，才能知道總共花多少時間、多少記憶體。

第三。有了遞迴公式之後，就必須安排出一套計算的順序。大問題的答案，總是以小問題的答案來求得的，所以，小問題的答案是必須先算的，否則大問題的答案從何而來呢？

一個好的安排方式，不但使程式碼容易撰寫，還可重複利用記憶體空間。

第四。記得先將最小、最先被計算的問題，心算出答案，儲存入表格，內建於程式碼之中。一道遞迴公式必須擁有初始值，才有辦法計算其他項。

第五。實作DP的程式時，會建立一個表格，在表格存入所有大小問題的答案。安排好每個問題的答案在表格的哪個位置，這樣計算時才能知道該在哪裡取值。

切勿存取超出表格的元素，產生溢位情形，導致答案算錯。計算過程當中，一旦某個問題的答案出錯，就會如骨牌效應般一個影響一個，造成很難除錯。

範例：樓梯路線（staircase walk），計數問題

一個方格棋盤，從左上角走到右下角，每次只能往右走一格或者往下走一格。請問有幾種走法？

對於任何一個方格來說，只可能「從上走來」或者「從左走來」，答案是兩者相加。

「從上走來」是一個規模更小的問題，「從左走來」是一個規模更小的問題，答案是兩者相加。

二維陣列的每一格對應每一個問題。設定第零行、第零列的答案，再以迴圈依序計算其餘答案。

時間複雜度分析：令H和W是棋盤長寬。計算一個問題需要O(1)時間（兩個子問題答案相加的時間）。總共HW個問題，所以計算所有問題需要O(HW)時間。

空間複雜度分析：總共HW個問題，所以需要O(HW)空間，簡單來說就是二維陣列啦！如果不需要儲存所有問題的答案，只想要得到其中一個特定問題的答案，那只需要一維陣列就夠了，也就是O(min(H,W))空間。

const int H = 8, W = 8; int f[H][W]; void staircase_walk() { // [initial states] for (int i=0; i<H; i++) f[i][0] = 1; for (int j=0; j<W; j++) f[0][j] = 1; // [computation] for (int i=1; i<H; i++) for (int j=1; j<W; j++) f[i][j] = f[i-1][j] + f[i][j-1]; // 輸出結果 cout << "由(0,0)走到(7,7)有" << f[7][7] << "種走法"; // cout << "由(0,0)走到(7,7)有" << f[H-1][W-1] << "種走法"; int h, w; while (cin >> h >> w) cout << "由(0,0)走到(h,w)有" << f[h][w] << "種走法"; }

節省記憶體是動態規劃的重要課題！

如果只打算求出一個問題，那麼只需要儲存最近算出來的問題答案，讓計算過程可以順利進行就可以了。

兩條陣列輪替使用，就足夠儲存最近算出來的問題答案、避免f[i-1][j]超出陣列範圍。

const int H = 8, W = 8; int f[2][W]; // 兩條陣列，儲存最近算出來的問題答案。 void staircase_walk() { // [initial states] for (int j=0; j<W; ++j) f[0][j] = 1; // [computation] for (int i=1; i<H; i++) for (int j=1; j<W; j++) // 只是多了 mod 2， // 外觀看起來就像兩條陣列輪替使用。 f[i % 2][j] = f[(i-1) % 2][j] + f[i % 2][j-1]; // 輸出結果 cout << "由(0,0)走到(7,7)有" << f[7 % 2][7] << "種走法"; // cout << "由(0,0)走到(7,7)有" << f[(H-1) % 2][W-1] << "種走法"; }

事實上，一條陣列就夠了。也不能再少了。

const int H = 8, W = 8; int f[W]; // 一條陣列就夠了 void staircase_walk() { // [initial states] for (int j=0; j<W; ++j) f[j] = 1; // [computation] for (int i=1; i<H; i++) for (int j=1; j<W; j++) f[j] += f[j-1]; // 輸出結果 cout << "由(0,0)走到(7,7)有" << f[7] << "種走法"; // cout << "由(0,0)走到(7,7)有" << f[W-1] << "種走法"; } const int H = 8, W = 8; int f[W]; // 一條陣列就夠了 void staircase_walk() { // [initial states] f[0] = 1; // 部分步驟移到[computation] // [computation] for (int i=0; i<H; i++) // 從零開始！ for (int j=1; j<W; j++) f[j] += f[j-1]; // 輸出結果 cout << "由(0,0)走到(7,7)有" << f[7] << "種走法"; // cout << "由(0,0)走到(7,7)有" << f[W-1] << "種走法"; }

如果某些格子上有障礙物呢？把此格設為零。

如果也可以往右下斜角走呢？添加來源f[i-1][j-1]。

如果可以往上下左右走呢？不斷繞圈子，永遠不會結束，走法無限多種。

UVa 10599 825 926

遞迴公式

若瞭解遞迴關係，就不必強記遞迴公式。若瞭解圖片意義，就不必強記數學符號。

f(i, j) =
 ⎧ 0                      , if i < 0 or j < 0     [exterior]
 ⎪ 1                      , if i = 0 or j = 0     [initial states]
 ⎨ f(i-1, j) + f(i, j-1)  , if i > 0 and i < 8    [computation]
 ⎪                          and j > 0 and j < 8
 ⎩ 0                      , if i >= 8 or j >= 8   [exterior]

f(i, j)：從格子 (0, 0) 走到格子 (i, j) 的走法數目。

遞歸方向

這個問題雙向都可以遞歸。對於任何一個方格來說，只可能「向右走出」或者「向下走出」。

範例：樓梯路線（staircase walk），極值問題

動態規劃的問題，可以分為「計數問題」和「極值問題」。方才介紹「計數問題」，現在介紹「極值問題」。

一個方格棋盤，格子擁有數字。從左上角走到右下角，每次只能往右走一格或者往下走一格。請問總和最小的走法？（或者總和最大的走法？）

const int H = 8, W = 8; int a[H][W]; int f[H][W]; void staircase_walk() { // [initial states] f[0][0] = a[0][0]; for (int i=1; i<H; i++) f[i][0] = f[i-1][0] + a[i][0]; for (int j=1; j<W; j++) f[0][j] = f[0][j-1] + a[0][j]; // [computation] for (int i=1; i<H; i++) for (int j=1; j<W; j++) f[i][j] = max(f[i-1][j], f[i][j-1]) + a[i][j]; // 輸出結果 cout << "由(0,0)走到(7,7)的最小總和" << f[7][7]; // cout << "由(0,0)走到(7,7)的最小總和" << f[H-1][W-1]; int h, w; while (cin >> h >> w) cout << "由(0,0)走到(h,w)的最小總和" << f[h][w]; }

想要印出路線，另外用一個陣列，記錄從哪走來。

const int H = 8, W = 8; int a[H][W]; int f[H][W]; int p[H][W]; int out[H+W-1]; void staircase_walk() { // [initial states] f[0][0] = a[0][0]; p[0][0] = -1; // 沒有源頭 for (int i=1; i<H; i++) { f[i][0] = f[i-1][0] + a[i][0]; p[i][0] = 0; // 從上走來 } for (int j=1; j<W; j++) { f[0][j] = f[0][j-1] + a[0][j]; p[0][j] = 1; // 從左走來 } // [computation] for (int i=1; i<H; i++) for (int j=1; j<W; j++) if (f[i-1][j] < f[i][j-1]) { f[i][j] = f[i-1][j] + a[i][j]; p[i][j] = 0; // 從上走來 } else if (f[i-1][j] > f[i][j-1]) { f[i][j] = f[i][j-1] + a[i][j]; p[i][j] = 1; // 從左走來 } else /*if (f[i-1][j] == f[i][j-1])*/ { // 從上走來、從左走來都可以，這裡取左。 f[i][j] = f[i][j-1] + a[i][j]; p[i][j] = 1; } // 反向追蹤路線源頭 int n = 0; // out size for (int i=H-1, j=W-1; i>=0 && j>=0; ) { out[n++] = p[i][j]; if (p[i][j] == 0) i--; else if (p[i][j] == 1) j--; } // 印出路線 for (int i=n-1; i>=0; --i) cout << out[i]; }

額外介紹一個技巧。為了避免減一超出邊界，需要添補許多程式碼。整個棋盤往右下移動一格，就能精簡許多程式碼。

const int H = 8, W = 8; int a[H+1][W+1]; // 整個棋盤往右往下移動一格 int f[H+1][W+1]; // 全域變數，將自動初始化為零。 int p[H+1][W+1]; int out[H+W-1]; void staircase_walk() { // [initial states] // [computation] for (int i=1; i<=H; i++) for (int j=1; j<=W; j++) if (f[i-1][j] < f[i][j-1]) { f[i][j] = f[i-1][j] + a[i][j]; p[i][j] = 0; // 從上走來 } else /*if (f[i-1][j] >= f[i][j-1])*/ { f[i][j] = f[i][j-1] + a[i][j]; p[i][j] = 1; // 從左走來 } // 反向追蹤路線源頭 int n = 0; // out size for (int i=H, j=W; i>0 && j>0; ) { out[n++] = p[i][j]; if (p[i][j] == 0) i--; else if (p[i][j] == 1) j--; } // 印出路線 for (int i=n-1; i>=0; --i) cout << out[i]; } const int H = 8, W = 8; int a[H+1][W+1]; // 整個棋盤往右往下移動一格 int f[H+1][W+1]; // 全域變數，將自動初始化為零。 int p[H+1][W+1]; int out[H+W-1]; void staircase_walk() { // [initial states] // [computation] const int h[2] = {1, 0}; const int w[2] = {0, 1}; for (int i=1; i<=H; i++) for (int j=1; j<=W; j++) { if (f[i-1][j] < f[i][j-1]) p[i][j] = 0; else p[i][j] = 1; int& d = p[i][j]; f[i][j] = f[i-h[d]][j-w[d]] + a[i][j]; } // 反向追蹤路線源頭 int n = 0; // out size for (int i=H, j=W; i>0 && j>0; ) { int& d = p[i][j]; out[n++] = d; i -= h[d]; j -= w[d]; } // 印出路線 for (int i=n-1; i>=0; --i) cout << out[i]; }

範例：樓梯路線（staircase walk），極值問題

節省記憶體是動態規劃當中重要的課題！

方才的分割方式：分割最後一步，窮舉最後一步從哪走來；方才的實作方式：由小到大的迴圈。問題答案f[i][j]，可以精簡成一維陣列。路線來源p[i][j]，無法精簡成一維陣列。

想讓路線來源精簡成一維陣列，必須採用另一種分割方式：從地圖中線分割，窮舉穿過中線的所有地點；同時採用另一種實作方式：由大到小的遞迴。

state / DAG

以state和DAG的觀點，重新看待動態規劃。

動態規劃得類比成「狀態state」：「問題」變「狀態」，「全部問題」變「狀態空間」，「遞迴關係」變「狀態轉移函式」。

動態規劃得類比成「有向無環圖DAG」：既然遞迴關係不能循環，顯然就是DAG。「問題」變「點」，「遞迴關係」變「邊」，「計算順序」變「拓撲順序」。

即便讀者不懂state和DAG也沒關係，只要抓住兩個要點：每個小問題各是一個狀態，只有數值範圍不同；狀態之間是單行道，依序求解，不能循環。

範例：爬樓梯（climbing stairs）

f(n) =
 ⎧ f(n-1) + f(n-2)  , if n > 2
 ⎨ 2                , if n = 2
 ⎩ 1                , if n = 1

一維狀態。兩個子問題。

時間複雜度O(N)。空間複雜度O(1)。

const int N = 5; int f[N+1]; int climbing_stairs() { f[0] = 0; f[1] = 1; for (int i=2; i<=N; ++i) f[i] = f[i-1] + f[i-2]; return f[N]; }

範例：河內塔（tower of Hanoi）

f(n) =
 ⎰ f(n-1) + 1 + f(n-1)  , if n > 1
 ⎱ 1                    , if n = 1

除了子問題，還附帶其他成本。

時間複雜度O(N)。空間複雜度O(1)。

const int N = 5; int f[N+1]; int tower_of_hanoi() { f[0] = 0; for (int i=1; i<=N; ++i) f[i] = f[i-1] * 2 + 1; return f[N]; }

範例：樓梯路線（staircase walk）

f(h, w) =
 ⎰ f(h-1, w) + f(h, w-1)  , if h > 1 and w > 1
 ⎱ 1                      , if h = 1 or w = 1

二維狀態。兩個子問題。

時間複雜度O(HW)。空間複雜度O(HW)。

const int H = 8, W = 8; int f[H][W]; int staircase_walk() { for (int i=0; i<H; i++) f[i][0] = 1; for (int j=0; j<W; j++) f[0][j] = 1; for (int i=1; i<H; i++) for (int j=1; j<W; j++) f[i][j] = f[i-1][j] + f[i][j-1]; return f[H-1][W-1]; }

表格可以重複利用。空間複雜度降為O(W)甚至O(min(H,W))。

const int H = 8, W = 8; int f[W]; int staircase_walk() { for (int j=1; j<W; j++) f[j] = 1; for (int i=1; i<H; i++) for (int j=1; j<W; j++) f[j] = f[j] + f[j-1]; return f[W-1]; }

範例：組合（combination）

f(n, m) =
 ⎰ f(n-1, m-1) + f(n-1, m)  , if n > 1 and m > 1 and m < n
 ⎱ 1                        , if n = 1 or n = m

二維狀態。兩個子問題。

時間複雜度O(N²)。空間複雜度O(N²)。

const int N = 9, M = 7; int f[N+1][N+1]; int combination() { for (int i=0; i<=N; ++i) f[i][0] = f[i][i] = 1; for (int i=1; i<=N; ++i) for (int j=1; j<i; ++j) f[i][j] = f[i-1][j-1] + f[i-1][j]; return f[N][M]; }

組合數表格，即是巴斯卡三角形。巴斯卡三角形靠左對齊，視覺上就可以一一對應至表格。巴斯卡三角形左右對稱，對稱部分可以精簡。

表格可以只用一半。空間複雜度仍然相同。但是沒有意義。個人電腦記憶體充足，節省一半差別不大。

const int N = 9, M = 7; int f[N][N/2+1]; int combination() { for (int i=0; i<=N; ++i) f[i][0] = 1; for (int i=2; i<=N; ++i) { int j; for (j=1; j<i/2; ++j) f[i][j] = f[i-1][j-1] + f[i-1][j]; // j = i/2; if (i % 2 == 0) f[i][j] = f[i-1][j-1] * 2; else f[i][j] = f[i-1][j-1] + f[i-1][j]; } return (M <= N/2) ? f[N][M] : f[N][N-M]; }

表格可以重複利用。空間複雜度降為O(N)。但是沒有意義。與其重複利用表格，不如直接使用公式解。

const int N = 9, M = 7; int f[N/2+1]; int combination() { f[0] = 1; for (int i=2; i<=N; ++i) { int j = i/2; if (i % 2 == 0) { f[j] = f[j-1] + f[j]; j--; } for (; j>=1; --j) f[j] = f[j-1] + f[j]; } return (M <= N/2) ? f[M] : f[N-M]; }

範例：矩陣相乘次序（matrix chain multiplication）

一連串矩陣相乘，無論從何處開始相乘，計算結果都一樣。

然而，計算時間卻有差異。兩個矩陣，大小為a x b及b x c，相乘需要O(abc)時間（當然還可以更快，但是此處不討論）。那麼一連串矩陣相乘，最少需要多少時間呢？

一連串矩陣，從最後一次相乘的地方分開，化作兩串矩陣相乘。考慮所有可能的分開方式。

f(i, k) =  min  { f(i, j) + f(j+1, k) + r[i] ⋅ c[j] ⋅ c[k] }
         j=i⋯k-1

f(i, k)：從第i個矩陣乘到第k個矩陣，最少的相乘次數。
r[i]：第i個矩陣的row數目。
c[i]：第i個矩陣的column數目。

時間複雜度O(N³)。空間複雜度O(N²)。

const int N = 10; int r[N], c[N]; int f[N][N]; int matrix_chain_multiplication() { memset(f, 0x7f, sizeof(f)); for (int i=0; i<N; ++i) f[i][i] = 0; for (int l=1; l<N; ++l) for (int i=0; i+l<N; ++i) { int k = i + l; for (int j=i; j<k; ++j) f[i][k] = min(f[i][k], f[i][j] + f[j+1][k] + r[i] * c[j] * c[k]); } return f[0][N-1]; }

計算順序可以調整成online版本。

for (int k=1; k<N; ++k) for (int i=k-1; i>=0; --i) for (int j=k-1; j>=i; --j) // for (int j=i; j<k; ++j) f[i][k] = min(f[i][k], f[i][j] + f[j+1][k] + r[i] * c[j] * c[k]);

同類型的動態規劃問題（只是順手整理，不是本節重點）：

matrix chain multiplication
optimal binary search tree
Hu–Tucker compression
minimum weight triangulation of convex polygon
Cocke–Younger–Kasami algorithm

UVa 348 442

範例：longest increasing subsequence

一連串數字，從左到右挑選數字，越來越大。最多幾個？

一連串數字，保留開頭幾個數字，隔離最後一個數字，化作一小串數字與一個新數字。考慮所有可能的保留方式。

f(j) = max ( 1, max { f(i) + ( a[i] < a[j] ? 1 : -∞ ) } )
              i=0⋯j-1

f(j)：前j個數字可以挑出的數字數量，而且第j個數字被挑出。
a[j]：第j個數字。

遞迴公式內含判斷式：嘗試讓數字更大且更多。

正確答案必須搜尋表格：枚舉每個問題，其答案最大者。

時間複雜度O(N²)。空間複雜度O(N)。

const int N = 100; int a[N]; int f[N]; int longest_increasing_subsequence() { for (int j=0; j<N; j++) { // 答案至少是1。 f[j] = 1; // 找出 s[i] 能接在哪些數字後面， // 若是可以接，長度就增加。 for (int i=0; i<j; i++) if (a[i] < a[j]) f[j] = max(f[j], f[i] + 1); } // 表格最大值即為答案。 int l = 0; for (int i=0; i<N; i++) l = max(l, f[i]); return l; }

同類型的動態規劃問題（只是順手整理，不是本節重點）：

longest increasing subsequence
longest common subsequence
longest palindromic subsequence

UVa 10900

設計狀態

設計狀態，目前沒有標準流程。變化多端、層出不窮。

正因如此，演算法競賽經常出現動態規劃問題，以便考驗選手思維。也因如此，選手經常探討如何設計狀態，以便應對各種動態規劃問題。關於設計狀態，也許大家可以請教競賽選手。競賽選手的網路文章、專家學者的學術論文，兩者相比，前者比較平易近人。

以下姑且提供一些個人經驗，即便我不擅長設計狀態。

設計狀態：狀態變數

簡易策略：所有未知變因，通通納入狀態變數。

一般來說，狀態變數越多，表格維度越大，計算時間越久。一般來說，狀態變數越少越好。

變數不一定是表面上看到的變因。例如「人潮最多的時段」，遞增的標的，是時刻，而不是訪客。

變數也有優先順序。例如「儲存座標」，變數有「點編號」和「座標軸編號」，優先順序導致表格造型改變、遞迴公式改變。

變數甚至可以是答案。答案納入狀態變數，等同於枚舉各種可能的答案。宛如試誤法。

變數甚至可以跟答案缺乏直接關聯。答案需要從表格抽取數字、重新計算而得。宛如預計算。

設計狀態：遞歸策略

變數減一。也可能減更多數值。

也可能需要枚舉許多個數值。

也可能需要複雜的公式。

也可能仰賴其他變數。

也可能包含判斷式。

bitset

bitset是一個二進位數字，每一個bit分別代表每一件東西，1代表開啟，0代表關閉。例如現在有十個燈泡，編號設定為零到九，其中第零個、第三個、第九個燈泡是亮的，剩下來的燈泡是暗的。我們用一個10 bit的二進位數字1000001001，表示這十個燈泡的亮暗狀態。

建立一個大小為2¹⁰的陣列，便囊括了所有可能的狀態。陣列的每一格，就代表一種燈泡開關的狀態。

int array[1<<10]; array[521] = 想記錄的數字; /* 1000001001(2進位) = 521(10進位) */

當狀態數量呈指數成長，可以利用bitset作為狀態。

UVa 10952

範例：maximum matching

以線相連的兩物，可以配對在一起。求最大配對數目暨配對方式。

「maximum matching」有多項式時間演算法，可是很難實作；動態規劃雖然慢了些，是指數時間演算法，但是容易實作。移除匹配成一對的點，就得到遞迴公式。

f(S+{i}+{j}) = max { f(S) + adj(i, j) }
              i,j∉S

f(S) = max { f(S-{i}-{j}) + adj(i, j) }
      i,j∈S

使用bitset，已匹配標成1，未匹配標成0。時間複雜度O(2ᴺ N²)，空間複雜度O(2ᴺ)。

這個演算法可以再修正，讓時間複雜度降為O(2ᴺ N)。各位可以試試看。

這個演算法需要大量記憶體，所以無法計算N很大的情況，何況編譯器也不准我們建立太大的陣列，N=28就是極限了。這個演算法同時也需要大量時間，以現在的個人電腦來說，N=17就已經要花上幾分鐘才能求出答案了。

// top-down DP const int N = 10; int adj[N][N]; // adjacency matrix。連線為1，否則為0。 int f[1<<N]; // dp table bool ok[1<<N]; // dp table是否已存值 //int p[1<<N][2]; // 記錄匹配方式，此處省略。 bool dp(int s) { if (s == 0) return true; if (ok[s]) return f[s]; for (int i=0; i<N; ++i) for (int j=i+1; j<N; ++j) if (s & ((1<<i) | (1<<j))) { // ss = s - {i} - {j}; int ss = s ^ (1<<i) ^ (1<<j); f[s] = max(f[s], dp(ss) + adj[i][j]); } ok[s] = true; return f[s]; } int maximum_matching() { memset(f, 0, sizeof(f)); memset(ok, false, sizeof(ok)); return dp((1<<N)-1); }

UVa 10888 10911 11439 10296 11156

範例：Hamilton path

找到一條路徑，剛好每一個點都去過一次。有可能找不到。

「Hamilton path」尚無多項式時間演算法。直覺的解法是backtracking，窮舉所有點的各種排列方式，一種排列方式當作一條路徑，判斷是不是Hamilton path。

運用動態規劃，可以減少計算時間。拆掉一條路徑的最後一條邊，就得到遞迴公式。需要額外維度，記錄路徑終點。

f(S+{j}, j) = or { f(S, i) and adj(i, j) }   where j∉S
              i∈S

f(S, j) = or { f(S-{j}, i) and adj(i, j) }   where j∈S
          i∈S
          i≠j

時間複雜度O(2ᴺ N²)，空間複雜度O(2ᴺ)。

const int N = 10; bool adj[N][N]; // adjacency matrix bool f[1<<N][N]; // dp table bool ok[1<<N][N]; // dp table是否已存值 bool dp(int s, int j) { if (s == (1<<j)) return true; // s只有一個位元是1 if (ok[s][j]) return f[s][j]; ok[s][j] = true; for (int i=0; i<N; ++i) if (i != j && s & (1<<i)) if (dp(s ^ (1<<j), i) && adj[i][j]) return f[s][j] = true; return f[s][j] = false; } bool hamilton_path() { memset(f, false, sizeof(f)); memset(ok, false, sizeof(ok)); for (int i=0; i<N; ++i) if (dp((1<<N)-1, N, i)) return true; return false; }

UVa 216 10068 10496 10818 10937 10944 10605 10890 265

範例：骨牌平舖（domino tiling）

中文網路稱作「插头DP」或「轮廓线DP」。

UVa 11741

範例：子集子集和（subset sum of subset）

英文網路稱作「sum over subsets DP」。

範例：不重複路線（self-avoiding walk），計數問題

先前介紹過樓梯路線（staircase walk）。樓梯路線問題，只能往兩個方向走，可以簡單的遞迴分割，得到多項式時間演算法。不重複路線問題，可以往四個方向走，無法簡單的遞迴分割，只有指數時間演算法。儘管如此，不重複路線還是可以使用動態規劃。

UVa 10572 10531

範例：不重複路線（self-avoiding walk），極值問題

極值問題反而存在多項式時間演算法！原問題化作圖：點有權重，邊無權重。原問題化作最短路徑：點權重挪至入邊權重。

請見本站文件「shorest path」。

dynamic programming speedup

極值問題有許多手法可以降低時間複雜度。根據recurrence的樣式，採取對應的手法。

詳細來說，一個問題（狀態）通常有許多個子問題。

計數問題：每一個子問題都納入統計。窮舉全部。

極值問題：找到最好的那一個子問題。挑選一個。

極值問題，只需要找到一個子問題，其答案最小（最大）。所有子問題，依照答案大小排序，就能快速找到那一個子問題，而不必逐一檢查。根據recurrence的樣式，採取對應的排序手法。

即時排序

詳細來說，極值問題當中，一個問題通常有許多個子問題（候選解），從中找到最好的那一個子問題（最佳解）。

正常做法：枚舉所有候選解，找出一個最佳解。

取巧做法：即時排序候選解，只枚舉一部分的候選解。

巧妙地安排計算順序，方便即時排序候選解。每個問題的候選解，彼此之間有關聯。下一個問題的候選解，繼承了上一個問題的候選解。不必重頭排序，只需微調順序。

候選解數值、候選解位置

詳細來說，即時排序的對象，可以分為兩種：候選解數值（樓梯路線的f陣列）、候選解位置（樓梯路線的p陣列）。

候選解數值：大家已經發現許多經典手法，例如stack/deque、envelope/convex hull、unimodal function、Monge matrix。

候選解位置：手法極少，例如Knuth–Yao speedup。

概論

F[n] = min/max { F[i] ⋅ W[i] + C[i] }
       i=0⋯n-1

F[n]是未知數，F[i] W[i] C[i]是已知數。計算到F[n]時，F[i]早已計算完畢，因此F[i]是已知數。

這種形式的recurrence，直接計算是O(N²)。此處介紹更快的演算法，降為O(N)。

stack

括號配對極值。stack保持嚴格遞增（嚴格遞減），即時移除多餘數值，即時獲取過往最大值（最小值）。

          for finding maximum,
          keep monotone increasing  ---->
      ┌──────┬──────┬──────┬─────────┬───────╯
stack │ M[2] │ M[4] │ M[6] │   ...   │ M[10]
      └──────┴──────┴──────┴─────────┴───────╮
                                      ^^^^^^^ extract maximum
               clean tails until monotonicity
               then push new M[i] into tail

M[i] = F[i] ⋅ W[i] + C[i]塞入尾端。塞入前，先彈出尾端數值們，使得M[i]塞入尾端之後，stack嚴格遞增。最大值從尾端取得。

範例：largest empty rectangle

詳見「largest empty rectangle」。

範例：all nearest smaller values

deque

滑動視窗極值。deque保持嚴格遞增（嚴格遞減），即時移除多餘數值，即時獲取過往最小值（最大值）。

           for finding minimum,
           keep monotone increasing  ---->
      ╰──────┬──────┬──────┬─────────┬───────╯
deque   M[2] │ M[4] │ M[6] │   ...   │ M[10]
      ╭──────┴──────┴──────┴─────────┴───────╮
       ^^^^^^                         ^^^^^^^
       extract minimum      clean tails until monotonicity
                            then push new M[i] into tail

M[i] = F[i] ⋅ W[i] + C[i]塞入尾端。塞入前，先彈出尾端數值們，使得M[i]塞入尾端之後，deque嚴格遞增。塞入後，再彈出頭端數值們，使得deque符合滑動視窗範圍。最小值從頭端取得。

中文網路稱作「单调队列优化」。

範例：maxium sum subarray

詳見「maxium sum subarray」。

範例：maximum average subarray

詳見「maxium average subarray」。

由於斜率是關鍵，因此中文網路稱作「斜率优化」。

概論

F[n] = min/max { F[i] ⋅ W[n] + C[i] }
       i=0⋯n-1

W[i]換成W[n]。處理方式大幅改變。

這種形式的recurrence，直接計算是O(N²)。此處介紹更快的演算法，降為O(Nlog²N)。

先備知識是「convex hull」、「point-line duality」、「Fenchel duality」。

envelope

直線y = F[i] x + C[i]，鉛直線x = W[n]，交點Y軸座標F[n]。

最小（大）值對應最低（高）交點。

最小（大）值位於下（上）包絡線。

convex hull

如果討厭包絡線，可透過點線對偶，從包絡線變成凸包。

直線穿過點(F[i], -C[i])，斜率W[n]，Y軸截距-F[n]。

垂直方向翻轉，讓最小（大）值對應最低（高）截距。

直線穿過點(F[i], C[i])，斜率-W[n]，Y軸截距F[n]。

最小（大）值位於下（上）凸包的切線，跟Y軸的交點。

如果不熟悉點線對偶，可透過移項推導，得到相同結論：

概論

根據F[i]與W[n]的性質，時間複雜度隨之變化：

一、W[n]皆相同：不必維護凸包，只需維護每個點在「斜率-W[n]的直線的垂直方向上」的先後順序，彷彿先前章節「deque加速」。一個常見的例子是W[n] = 1。O(N)。

中文網路稱作「单调队列优化」。

二、F[i]與W[n]皆單調：Andrew's monotone chain維護下凸包（求最小值時）。切線斜率-W[n]遞減/增。直接從上次切點開始，往左/右找到新切點。O(N)。

由於斜率遞增，中文網路也將此手法稱作「斜率优化」。

三、F[i]單調：Andrew's monotone chain 維護下凸包（求最小值時）。切線斜率-W[n]會變。三分搜尋找到切點，或者二元搜尋凸包斜率找到切點。O(NlogN)。

中文網路稱作「WQS二分」。

四、無特別性質：動態凸包資料結構。O(Nlog²N)。

中文網路稱作「李超线段树」。

UVa 12524

範例：1D p-median problem

詳見「p-median problem」。

範例：bounded knapsack problem

詳見「bounded knapsack problem」。

概論

F[n] = min/max { M[i] }
       i=0⋯n-1

M[i] is monotone/unimodal

根據M[i]的性質，時間複雜度隨之變化：

一、F[n]的子問題們，其答案M[0]...M[n-1]恰好是單調函數：根本沒啥好算，最佳解顯然是第一個（最後一個）子問題。O(N)。

二、F[n]的子問題們，其答案M[0]...M[n-1]恰好是單峰函數：三分搜尋山峰，或者二元搜尋斜率。O(NlogN)。

三、每個問題的單峰函數，山峰位置恰好遞增（往右移動）：用同一條掃描線尋找山峰。O(N)。

概論

什麼時候會是單峰函數呢？舉兩個例子。

F[n] =  min  { max(F[i], G[i]) + 5 }
      i=0⋯n-1

(1) F[i] is increasing
(2) G[i] is decreasing
(=>) max(F[i], G[i]) + 5 is unimodal

F遞增、G遞減，則max(F[i], G[i]) + 5是單峰函數。不過這個例子有點蠢，山谷恰好永遠不動。

F[n] =  min  { F[i] + G[i] }
      i=0⋯n-1

(1) F[i] is convex
(2) G[i] is convex
(=>) F[i] + G[i] is convex (also unimodal)

F G皆是凸函數，則F[i] + G[i]是凸函數，即是單峰函數。不過這個例子也有點蠢，山谷恰好永遠不動。

範例：egg drop

一堆蛋，已知耐力皆相同，不知耐力為多少。試求耐力。

耐力是以樓層衡量：大於某樓層，摔下必破，無法重複使用；小於等於某樓層，摔下必不破，完全不會折損，可以重複使用。

這個問題有許多變形，此處討論實驗場地是n層樓的情況：

一、最少摔破幾顆蛋？需要事先準備幾顆蛋？

答：一顆蛋。從一樓開始摔，逐步上樓，直到摔破為止。

二、無限多蛋，運氣不好時，最少摔幾次？

答：二元搜尋。F[0] = 0, F[1] = 1, F[n] = F[ceil((n-1)/2)] + 1。

三、一顆蛋，運氣不好時，最少摔幾次？

答：n次。耐力不幸是n樓，從一樓開始摔，要摔n次。

四、兩顆蛋，運氣不好時，最少摔幾次？

答：首發選在i樓。如果摔破了，剩下一顆蛋，只好從一樓開始測試；最差的情況，耐力是i-1樓，要摔i-1次。如果沒有摔破，仍是兩顆蛋，問題仍相同，範圍縮小成n-i樓。兩種情況取最大值。窮舉i，找到次數最少者。

F[n] = 1 +  min  { max(i-1, F[n-i]) }
           i=1⋯n

F[n] = 1 +  min  { max(i, F[n-1-i]) }   調整索引值
          i=0⋯n-1

i遞增，F[n-1-i]遞減，因此max(i, F[n-1-i])是單峰函數，而且山谷持續往右移動，可以使用掃描線解決。另外也有數學公式解：

五、k顆蛋，運氣不好時，最少摔幾次？

答：留給讀者。

UVa 10934 882

範例：isotonic regression

英文網路稱作「slope trick」。

範例：word wrap

詳見「word wrap」。

概論

F[n] = min/max { M[i][n] }
       i=0⋯n-1

M[i][n] is upper-triangular monotone/totally monotone/Monge

根據M[i][n]的性質，時間複雜度隨之變化：

一、M[i][n]是上三角monotone matrix：似乎沒有特別快的演算法，仍是O(N²)。

二、M[i][n]是上三角totally monotone matrix：兩個演算法，O(NlogN)與O(Nα(N))。此處只談第一個。

三、M[i][n]是上三角Monge matrix：至今仍然沒有專屬演算法。大家直接沿用totally monotone matrix的演算法。

三種矩陣皆細分成凹凸兩種情況。兩種情況的演算法稍微不同。此處均介紹。

三種矩陣當中，以Monge matrix最為常見。它也是性質最強的矩陣，若三成立則二成立，若二成立則一成立。

本文當中，「上三角Monge matrix」並非是「下三角恰為0的Monge matrix」，而是「僅上三角符合Monge matrix」。

Monge matrix的定義，在古代曾經稱作quadrangle inequality，導致中文網路稱作「四边形不等式优化」。

先備知識是「pairwise distance」。

概論

F[n] = min/max { F[i] ⋅ W[i] + C[i][n] }
       i=0⋯n-1

(1) C[i][n] is upper-triangular Monge
(=>) M[i][n] = F[i] ⋅ W[i] + C[i][n] is upper-triangular Monge

Monge matrix橫條加上同一數，仍是Monge matrix。藉由這個數學性質，我們得以處理這種形式的recurrence。

這種形式的recurrence，直接計算是 O(N²)。此處介紹更快的演算法，降為O(NlogN)。

convex totally monotone matrix

大意：直條最小值位置往上遞減。使用stack。

首先畫出C[i][n]，一個上三角矩陣。圖片省略了實際數值。

計算F[1]：F[0] ⋅ W[0]加到C[0][1]即得。

計算F[2]：F[0] ⋅ W[0]加到C[0][2]，F[1] ⋅ W[1]加到C[1][2]，取直條C[:][2]最小值。

以此類推。時間複雜度O(N²)。

重新反省計算過程，改良演算法：

一、算出F[i]之後，F[i] ⋅ W[i]加到對應的橫條，比較省事。

二、計算F[i]，即是取直條最小值。隨時記錄每個直條的最小值位置，每次F[i] ⋅ W[i]加到對應的橫條，順手更新最小值位置。

得到一個更容易解釋的演算法。時間複雜度仍是O(N²)。

凸全單調矩陣（直條版本），每個子矩陣都是凸單調矩陣，直條最小值位置總是往上遞減！

算出F[i]之後，從左往右更新最小值位置。最小值位置可能變i、可能不變。變與不變有著唯一一條分界線，左側一律變i，右側一律不變，以滿足遞減性質。

雖然可以提早break，但是時間複雜度仍是O(N²)。

位置相同者，合併成一個區間，最多N個區間。每當更新最小值位置，從左往右判斷每個區間的右端位置，直到遭遇不變的位置。然後二元搜尋該區間，找到分界線。

使用stack實作，一筆資料有兩個參數：區間右端的直條編號、最小值位置。每回合pop一些區間、做一次二元搜尋、push一個區間。時間複雜度O(NlogN)。

concave totally monotone matrix

大意：直條最小值位置往下遞增。使用deque。

改成從右往左更新最小值位置。時間複雜度O(NlogN)。

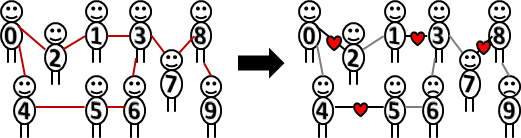
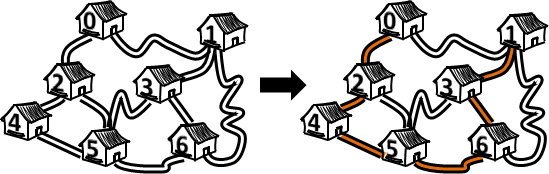
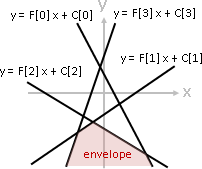
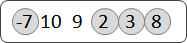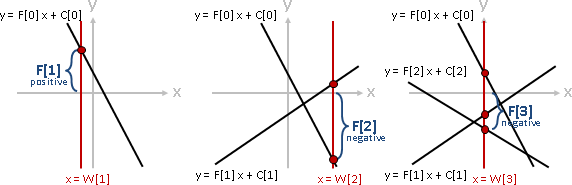概論

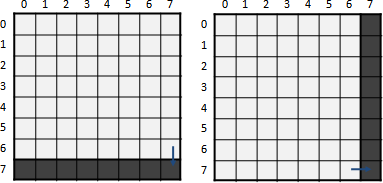
最佳解位置，恰好已排序。

每個問題，依照大小排序。最佳解位置，恰好也依照大小排序。

一個問題不必枚舉所有候選解。參考先前問題的最佳解位置，一個問題只需要枚舉一部分的候選解。

中文網路稱作「决策单调性」。

Knuth–Yao speedup

F[i,j] =  min  { F[i,k] + F[k+1,j] + C[i,j] }
        k=i⋯j-1

(1) C[i,j] is Monge*:  C[a,b] + C[a+1,b+1] ≤ C[a,b+1] + C[a+1,b]
(2) C[i,j] is sorted:  C[a,b] ≤ C[a,b+1] and C[a,b] ≤ C[a-1,b]
                       (C[a,b] ≤ C[c,d] when [a,b] ⊆ [c,d])
(=>) F[i,j] is Monge*
(=>) P[i,j] is sorted: P[a,b] ≤ P[a,b+1] and P[a,b] ≤ P[a+1,b]
                       (P[a,b-1] ≤ P[a,b] ≤ P[a+1,b])

*non-negative upper-trianglar concave Monge

(1) C[i,j] is Monge:   ↖ + ↘ ≤ ↗ + ↙       (concave)
(2) C[i,j] is sorted:  ← ≤ → and ↓ ≤ ↑     (toward ↗)
                       (←↙↓ ≤ →↗↑)
(=>) F[i,j] is Monge
(=>) P[i,j] is sorted: ← ≤ → and ↑ ≤ ↓     (toward ↘)
                       (↖ ≤ ↗ ≤ ↘)

這種形式的recurrence，直接計算是O(N³)。此處介紹更快的演算法，降為O(N²)。

附帶成本C[i,j]既是Monge matrix又是sorted matrix，導致最佳解數值F[i,j]是Monge matrix，也導致最佳解位置P[i,j]是sorted matrix。【待補證明】

一個問題的最佳解位置，範圍限縮。原本是a ≤ P[a,b] ≤ b，現在是P[a,b-1] ≤ P[a,b] ≤ P[a+1,b]。Monge matrix夾住左邊界，sorted matrix夾住右邊界。候選解變少，時間複雜度變低。

過程當中使用了Monge matrix，導致中文網路也將此手法稱作「四边形不等式优化」。

英文網路稱作「Knuth's optimization」。

範例：optimal binary search tree

N筆資料，欲建立成一棵「binary search tree」。並且預測了每筆資料的搜尋次數。

請問binary search tree是什麼形狀，才能讓拜訪到的節點數量最少呢？也就是說，每個節點的「深度」乘上「搜尋次數」，總和要最小。

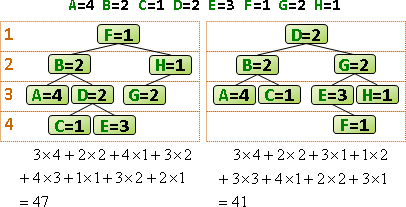
遞迴公式類似於matrix chain multiplication，都是記錄區間。窮舉樹根，分割成左右兩棵子樹遞迴下去。問題總共O(N²)個，一個問題要窮舉O(N)種分割點，時間複雜度O(N³)。

// 陣列邊界左右各加一格，避免判斷陣列邊界，省去麻煩。 int a[8+2] = {0, 4, 2, 1, 2, 3, 1, 2, 1, 0}; int sum[8+2]; // 累積和 int f[8+2][8+2]; // 每個節點「深度」乘上「搜尋次數」的總和 int p[8+2][8+2]; // 樹根，也就是分割點。 // 區間和 int c(int i, int j) {return sum[j] - sum[i-1];} void optimal_binary_search_tree() { for (int i=1; i<=8; ++i) sum[i] = sum[i-1] + a[i]; for (int i=1; i<=8; ++i) { f[i][i] = a[i]; p[i][i] = i; } // 計算順序為online版本 for (int k=2; k<=8; ++k) // 區間終點 for (int i=k-1; i>=1; --i) // 區間起點 { f[i][k] = 1e9; for (int j=i; j<=k; ++j) // 分割點 if (f[i][j-1] + f[j+1][k] + c(i,k) < f[i][k]) { f[i][k] = f[i][j-1] + f[j+1][k] + c(i,k); p[i][k] = j; } } cout << "總共拜訪到的節點數量" << f[1][8]; }

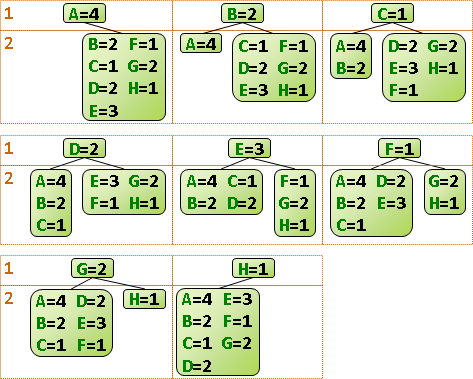
由於第二層迴圈的c(i,k)維持定值，不會影響最大值的判斷結果，所以可以挪到迴圈外面，減少加法次數，減少執行時間。

for (int k=2; k<=8; ++k) // 區間終點 for (int i=k-1; i>=1; --i) // 區間起點 { f[i][k] = 1e9; for (int j=i; j<=k; ++j) // 分割點 if (f[i][j-1] + f[j+1][k] < f[i][k]) { f[i][k] = f[i][j-1] + f[j+1][k]; p[i][k] = j; } // 挪到迴圈外面，最後再加上去。 f[i][k] += c(i,k); }

總共O(N²)個問題，每個問題必須窮舉O(N)個分割點，時間複雜度O(N³)。

到這裡都和普通的dynamic programming沒兩樣。接下來要更進一步。

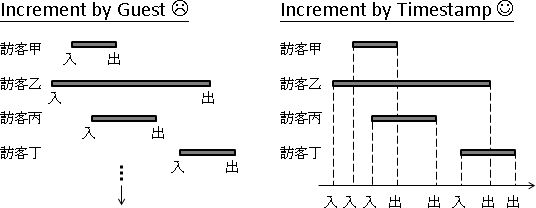
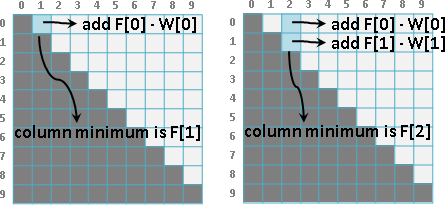
每次計算一個問題，總是得窮舉所有的分割點。然而有些分割點顯然是錯誤的，尤其是靠近區間邊界的那些分割點，實在不太可能將兩棵子樹分割的夠均勻、令總和最小。

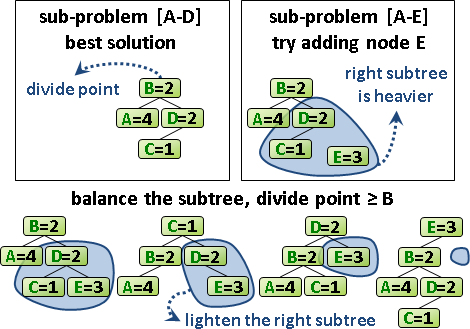
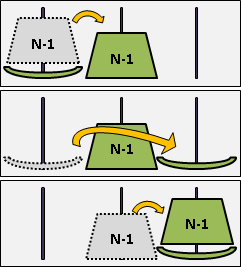
相近的問題，其分割點也很相近。問題[a,b]，嘗試從從右端拿掉一筆資料，成為問題[a,b-1]。問題[a,b]、問題[a,b-1]的分割點很相近。

為了讓左右子樹均勻，[a,b]的分割點一定要大於等於[a,b-1]的分割點，才能降低總和。小於[a,b-1]的分割點，沒有窮舉的必要，樹只會越不平衡、總和只會更大不會更小！

問題[a+1,b]的情況也十分類似，不再贅述。

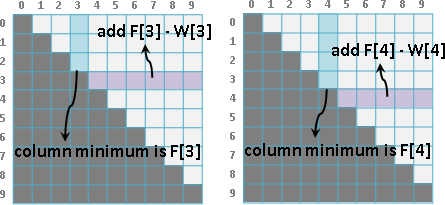
也就是說，問題[a,b]的分割點，必定位於更小的問題[a,b-1]和[a+1,b]的分割點之間。計算一個問題，大可不必窮舉所有的分割點。

for (int j=p[i][k-1]; j<=p[i+1][k]; ++j) // 分割點

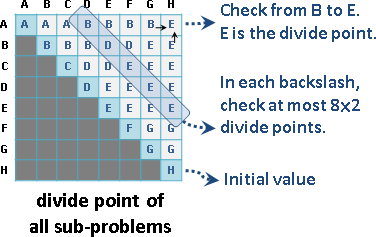
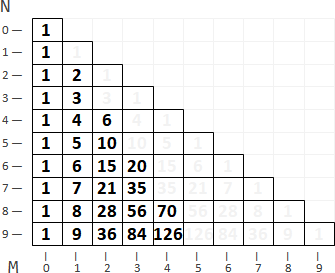
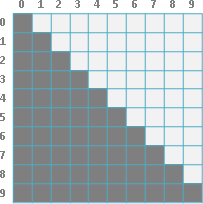
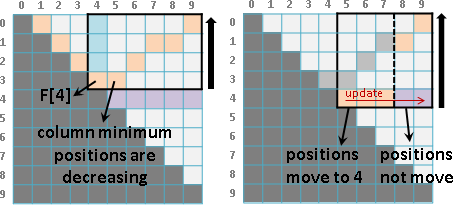
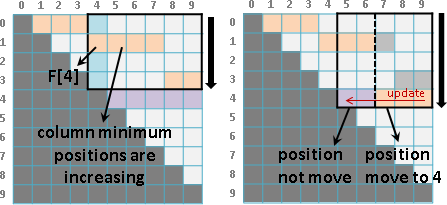
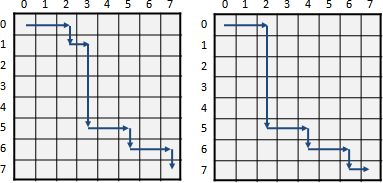
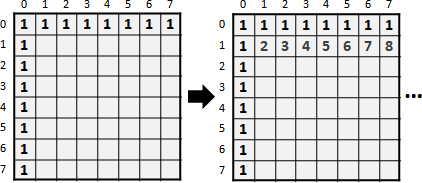
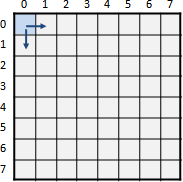
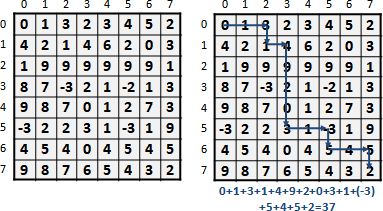
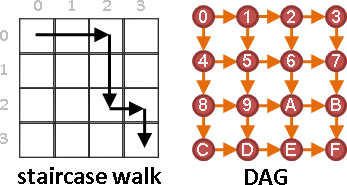
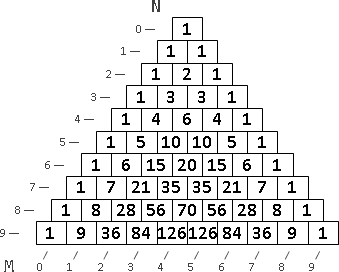
觀察分割點表格，[a,b-1]是左方格子，[a+1,b]是下方格子。要計算一個分割點，窮舉範圍就是左方格子的值到下方格子的值。也就是說每一個格子都會大於等於左方格子、小於等於下方格子。

每一條左上右下斜線，左上最小值是0，右下最大值是N-1，每一條斜線最多窮舉2N = O(N)個分割點。

除了初始值之外，總共N-1條斜線，需要窮舉的分割點總共O(N²)個，所以時間複雜度降為O(N²)。

UVa 10304 10003 12057 12809

Hu–Shing speedup

F[i,j] =  min  { F[i,k] + F[k+1,j] + C[i,j,k] }
        k=i⋯j-1

這種形式的recurrence，直接計算是O(N³)。此處介紹更快的演算法，降為O(NlogN)。

範例：matrix chain multiplication

我沒有研究。論文上百頁，我不想讀。

【尚無正式名稱】

F[i][j] =  min  { F[i-1][k-1] + C[k,j] }
          k=1⋯j

(1) C[i,j] is Monge: C[a,b] + C[a+1,b+1] ≤ C[a,b+1] + C[a+1,b]
(=>) P[i][j] is row-sorted: P[i,j] ≤ P[i,j+1]

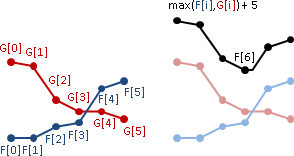
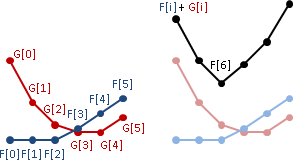
(2) C(|i-j|) is convex
(=>) F[i][j] is row-sorted
(=>) F[i-1][k-1] + C[k,j] is unimodal

這種形式的recurrence，直接計算是O(NM²)。此處介紹更快的演算法，降為O(NM)。

一、附帶成本C[i,j]恰是Monge matrix，導致最佳解位置P[i][j]是row-sorted matrix。【尚待確認】

一個問題的最佳解位置，範圍限縮。Monge matrix夾住左邊界。因為沒有夾住右邊界，所以用二分法處理右邊界。O(NMlogM)。

英文網路稱作「divide-and-conquer optimization」。

二、附帶成本C(|i - j|)恰是convex function，再導致最佳解數值F[i][j]是row-sorted matrix，也導致候選解數值F[i][k] + C[k,j]是unimodal function。【尚待確認】

一個問題的最佳解位置，範圍限縮。Monge matrix夾住左邊界。convex function夾住右邊界。O(NM)。

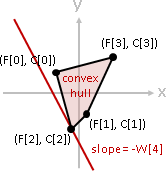
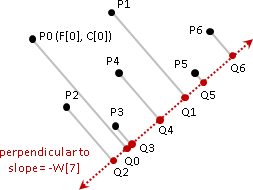
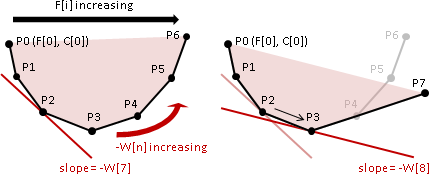
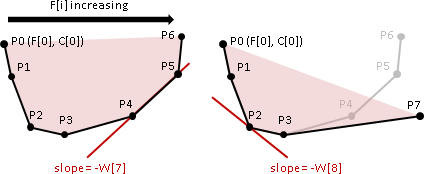
三、不管C[i,j]是什麼了。先前章節「convex hull加速」實施N次。W[n] = 1，彷彿「deque加速」。O(NM)。

範例：1D p-center problem

詳見「p-center problem」。

參考文獻

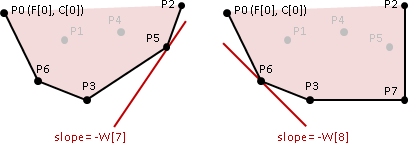
[envelope/convex hull] [unimodal function]
using geometric techniques to improve dynamic programming algorithms for the economic lot-sizing problem and extensions

[Monge matrix]
dynamic programming with convexity, concavity and sparsity
an almost linear time algorithm for generalized matrix searching

[Knuth–Yao speedup]
optimum binary search trees
efficient dynamic programming using quadrangle inequalities

[Hu–Shing speedup]
computation of matrix chain products, part I, part II
revisiting “computation of matrix chain products”