Binary Search Tree

「二元搜尋樹」。置放大量數字並且進行排序的資料結構。原理是Divide-and-Conquer Method，樹根居中，左子樹較小或相等，右子樹較大，然後遞迴分割下去。

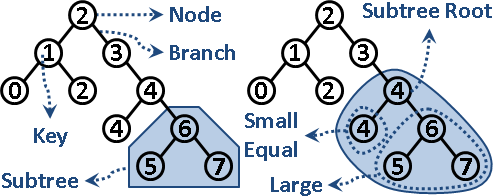
最小節點：從樹根開始往左小孩走到底。最大節點：從樹根開始往右小孩走到底。時間複雜度等同於二元搜尋樹的高度。

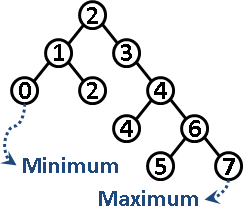
次小節點：先往左小孩走一步、再往右小孩走到底。如果一開始沒有左小孩，就往右上父親走到底，再往左上父親走一步就可以了。次大節點：方法類似。時間複雜度等同於二元搜尋樹的高度。

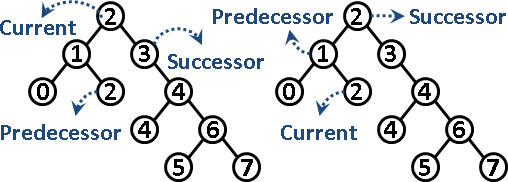
樹葉可以額外建立線索（Thread），左小孩連往次小節點，右小孩連往次大節點，如此就能迅速地依照次序走訪節點。建立線索不影響時間複雜度與空間複雜度。實作僅需迴圈、毋需遞迴。

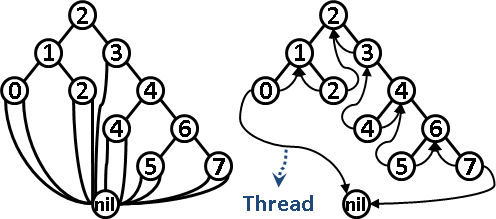
搜尋數字：從樹根開始走往左小孩或右小孩，直至目標。

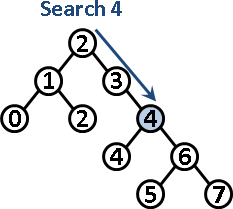
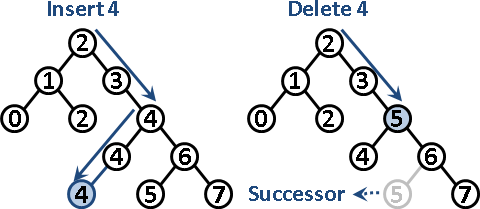
插入數字：搜尋直至樹葉。接著新增左小孩或右小孩。

刪除數字：搜尋直至目標。接著分為三類情況。沒有小孩：直接刪除節點。一個小孩：小孩連往父親，然後刪除節點。兩個小孩：次大節點取代目標節點。因為次大節點沒有左小孩，所以刪除次大節點只有兩類情況，於是到此為止不再遞迴。

搜尋、插入、刪除的時間複雜度等同於二元搜尋樹的高度。

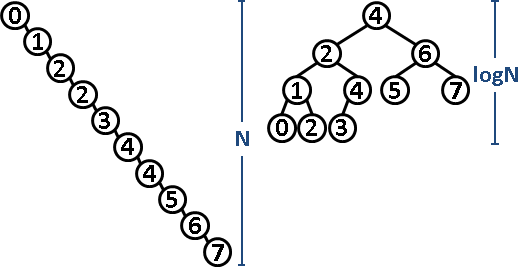
數字動態增減，二元搜尋樹的高度亦隨之變動，最差是O(N)，最佳是O(logN)。所有節點連成一線的時候是最差的，所有節點形成perfect binary tree是最佳的。

空間複雜度等同於節點數目，空間複雜度O(N)。

自平衡二元搜尋樹（Self-balancing Binary Search Tree）

每當數字動態增減，則即時調整每個節點的位置，即時調整每棵子樹的高度，讓整棵二元搜尋樹的高度維持是O(logN)，讓各項操作維持是O(logN)。

稍後介紹的AVL Tree、Red–Black Tree、Splay Tree，都是自平衡二元搜尋樹。

最佳二元搜尋樹（Optimum Binary Search Tree）

如果數字不會動態增減，則依照每個節點被搜尋到的次數（頻率），使用Dynamic Programming求得結構最佳的二元搜尋樹，藉此減少搜尋時間。建立時間為O(N²)。

UVa 10304

擴充二元搜尋樹（Augmented Binary Search Tree）

二元搜尋樹的每個節點，可以擴充資訊，例如子樹的高度、節點總數、數字總和、數字最大值、數字最小值、……。

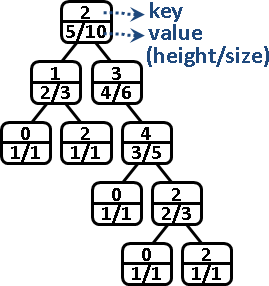
名次（Rank）

二元搜尋樹雖然有排序的功效，但是卻沒有排名的功效。想要排名，必須在每個節點新增一個變數，記錄其子樹的節點個數。不影響時間複雜度與空間複雜度。

第k名的節點：從根往葉，取得左小孩的節點個數，判斷第k名位於左子樹還是右子樹。時間複雜度等同於二元搜尋樹的高度。

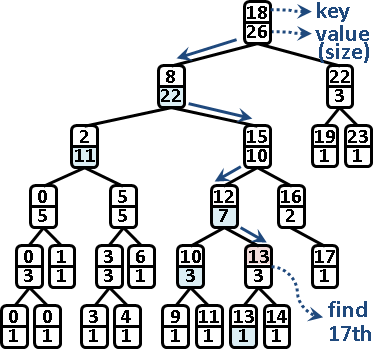
節點是第幾名：從葉往根，累計左子樹的節點個數，判斷當前節點是左小孩或右小孩以決定是否累計。時間複雜度等同於二元搜尋樹的高度。

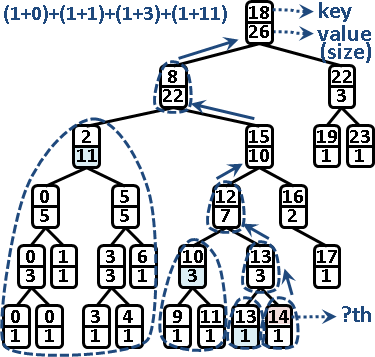
UVa 10909

AVL Tree（Balanced Binary Search Tree）

「AVL樹」。每一個節點（每一棵子樹），左子樹與右子樹的高度差最多為一。此舉造成二元搜尋樹的高度最多是1.44logN = O(logN)，讓各項操作穩定運行，不會產生忽快忽慢的極端現象。

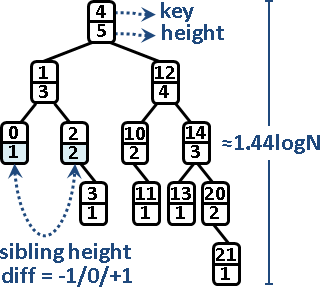
旋轉：改變連接方式，調整高度差。時間複雜度O(1)。

旋轉不影響次序，但是會影響分割基準，使得右子樹較大或相等，導致搜尋、插入、刪除完全失效。AVL Tree必須數字相異。

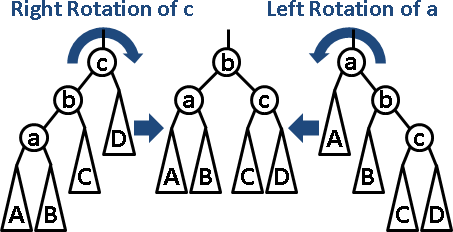
每次插入、刪除之後，馬上旋轉，讓整棵樹平衡。

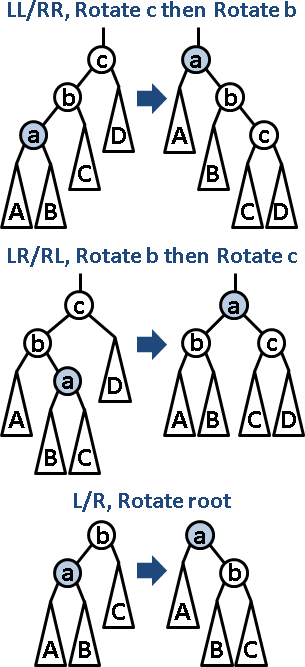
插入平衡：沿著插入路線，找到最深、高度差超過一的節點（子樹），接著分為四類情況。左左/右右：旋轉子樹樹根，立即平衡。左右/右左：先旋轉子樹樹根的左/右小孩，成為左左/右右，後續同前。旋轉一至兩次，就使整棵樹平衡。時間複雜度O(1)。

刪除平衡：沿著刪除路線，找到高度差超過一的節點。旋轉次數等同於二元搜尋樹的高度。時間複雜度O(logN)。

struct Node { Node* l, *r; // 左小孩、右小孩 int key; // 數字 int h, s; // 子樹高度（必須用到）、子樹大小 Node(int key): l(0), r(0), h(1), s(1), key(key) {} void update(); } *root = 0; // 想要少打幾個字，但是因為C++沒有with關鍵字，所以移到Node裡面。 void Node::update() { h = 1 + max(l?l->h:0, r?r->h:0); s = (l?l->s:0) + 1 + (r?r->s:0); } Node* rotateL(Node* x) // 左旋轉 { Node* y = x->r; x->r = y->l; y->l = x; x->update(); y->update(); return y; } Node* rotateR(Node* x) // 右旋轉 { Node* y = x->l; x->l = y->r; y->r = x; x->update(); y->update(); return y; } // 忘了做null檢查，會當機。 Node* balance(Node* x) { x->update(); if (x->l->h > 1 + x->r->h) { if (x->l->l->h < x->l->r->h) x->l = rotateL(x->l); x = rotateR(x); } else if (x->r->h > 1 + x->l->h) { if (x->r->r->h < x->r->l->h) x->r = rotateR(x->r); x = rotateL(x); } return x; } // 沿途判斷是否要旋轉，差勁的實作方式。 Node* insert(Node* x, int key) { if (x == 0) return new Node(key); if (key < x->key) x->l = insert(x->l, key); else if (key > x->key) x->r = insert(x->r, key); else return x; // 已有相同數字。直接結束。 return balance(x); } void insert(int key) { root = insert(root, key); }

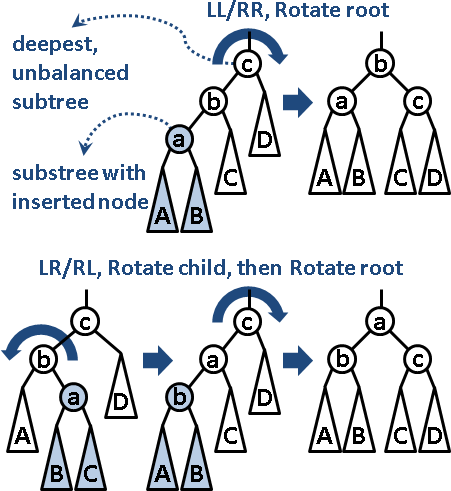
UVa 11688

Red–Black Tree

「紅黑樹」。沒有完全平衡，高度最多是2logN。

紅黑樹規則複雜，速度慢，此處不介紹。

早期謠言：AVL Tree高度均勻、搜尋快、插入刪除慢；Red–Black Tree與之相對。

近期實測：日常應用，AVL Tree比Red–Black Tree快20%。隨機亂數，差異不明顯。

https://benpfaff.org/papers/libavl.pdf

可以直接使用C++標準函式庫的set、map。

Splay Tree

「伸展樹」。沒有完全平衡，不過大致平衡。

伸展：把一個節點不斷雙旋至根。徹底縮短搜尋路線。也讓整棵樹更平衡。

每次插入、刪除之後，馬上伸展。此舉使得搜尋、插入、刪除、伸展的均攤時間複雜度成為O(logN)。

const int V = 10000+1; // 第零格不使用 int parent[V], child[V][2]; // 父親、左右小孩 int key[V]; // 數字 int height[V], size[V]; // 子樹高度、子樹大小 int T = 0, root = 0; // 節點數、根 #define l(i) child[i][0] #define r(i) child[i][1] // 建立節點 int create(int n) { int i = ++T; l(i) = r(i) = 0; height[i] = size[i] = 1; key[i] = n; return i; } // 更新擴充資訊 void update(int i) { height[i] = 1 + max(height[l(i)], height[r(i)]); size[i] = 1 + size[l(i)] + size[r(i)]; } // 判斷自己是左小孩或右小孩 int side(int i) { return r(parent[i]) == i; } // 旋轉 void rotate(int x, int r) { int y = parent[x]; if (parent[y]) child[parent[y]][side(y)] = x; child[y][r] = child[x][!r]; child[x][!r] = y; parent[x] = parent[y]; if (child[y][r]) parent[child[y][r]] = y; parent[y] = x; update(y); } // 雙旋至根 void splay(int x) { while (int y = parent[x]) { int rx = side(x), ry = side(y); if (!parent[y]) rotate(x, rx); else if (rx == ry) rotate(y, ry), rotate(x, rx); else rotate(x, rx), rotate(x, ry); } update(x); } // 插入 void insert(int n) { if (!root) {root = create(n); return;} int i = root; while (int j = child[i][n > key[i]]) i = j; int j = create(n); parent[j] = i; child[i][n > key[i]] = j; splay(j); root = j; } void splay_tree() { int n; while (cin >> n) insert(n); }

Weak AVL Tree / Relaxed AVL Tree

「弱AVL樹」。樹葉等級是0。父親等級多1或2。升級、降級、旋轉：調整等級。插入平衡：升級平均5次，旋轉1至2次。刪除平衡：降級平均1次，旋轉1至2次。《Rank-Balanced Trees》。

「鬆弛AVL樹」。樹葉等級非負。父親等級相等或更高。等級大於等於高度。不做刪除平衡。《Deletion Without Rebalancing in Binary Search Trees》。

僅有理論上的價值，沒有實務上的價值。

T-Tree

Binary Search Tree再進化！一個節點改為儲存大量數字，以符合傳輸通道大小、減少傳輸次數。適用「每次讀取需要很多準備時間、一次可以讀取一連串資料」的設備，例如硬碟、網路資料庫。

異地資料，存取時間約是計算時間的一千倍！我們關心存取時間（存取次數），不太關心計算時間（時間複雜度）。儘管T-Tree的搜尋、插入、刪除遠比Binary Search Tree冗長，但是T-Tree存取節點的次數較少！這是I/O-efficient Algorithm的經典範例。

插入、刪除過程繁複，動用許多節點。後來又發明了T*-Tree，盡可能直接編輯鄰近節點，避免新增、刪除、搬移節點。

B-Tree

T-Tree再進化！一個節點改為儲存大量數字和大量分枝。

網路已有詳細的教學和動畫，請讀者自行搜尋。

一、一個節點，可儲存m個分枝、m-1個數字。
二、一個節點，數字由小到大，循序儲存。
三、所有樹葉，位於同一層。
四、小孩數量等於數字數量加一。（排除樹葉）
五、小孩數量上下限是[ceil(m/2) , m]。（排除樹葉）
六、樹根不考慮小孩數量上下限。

插入、刪除過程繁複，動用許多節點。後來又發明了B⁺-Tree與B*-Tree，盡可能直接編輯鄰近節點，避免新增、刪除、搬移節點。

Skip Lists

置放大量數字並進行排序的資料結構。不使用樹狀結構，而是改用高度不同的List。概念上可以重新表示成Left-Child/Right-Sibling Binary Tree。這是Cache-efficient Algorithm的經典範例。

時間複雜度與空間複雜度與Binary Search Tree皆相同，但是實際運作效率比Binary Search Tree還要好。

Priority Queue

置放大量數字，可以隨時塞入數字、隨時彈出極值（最小值、最大值，只能選一種）的資料結構，泛稱Priority Queue。

泛稱是用來凸顯資料結構的功能。有了這樣的泛稱，當遇到的問題隱含著queue與sort的概念，就能直覺聯想到Priority Queue資料結構，而不會被Heap、Search Tree這種不直覺的名稱困住了思考。

極值是排序的特例

Heap    Search Tree
-------------------------
push    insert
pop     extremum + delete
peek    extremum
merge   merge

Heap的每一項操作，都能用Search Tree兜出來，時間複雜度完全一樣，唯一的例外是：Heap預先偷看極值，僅需O(1)時間；Search Tree則需O(logN)時間來搜尋極值。

如果在插入和刪除之時，隨時記錄極值，Search Tree還是能快速偷看極值。

Binary Heap

二元樹，樹根的數字，總是小於等於左右小孩的數字。

插入、刪除、求極值，時間複雜度O(logN)。

可以直接使用C++標準函式庫的priority_queue。

UVa 501 10587 11997

Binomial Heap

結合多個高度不同的Binomial Tree，宛如二進位系統。兩個Binomial Heap合併，宛如二進位加法。

特色是合併僅需O(logN)。

Fibonacci Heap

規則極其詭異，重點在於它有一個特殊功能叫做decrease key，可以搜尋數字，並且還可以減少該數字，時間複雜度均攤之後僅有O(1)。另外，插入的時間複雜度均攤之後僅有O(1)。

僅有理論上的價值，沒有實務上的價值。

Quake Heap

跟Fibonacci Heap功效相同，據說簡單很多。

僅有理論上的價值，沒有實務上的價值。

B-Heap

Binary Heap再進化！相鄰節點儲存於相鄰記憶體，劃分為區塊，減少存取次數。這是I/O-efficient Algorithm的經典範例。

van Emde Boas Tree（vEB Tree）

置放大量正整數（與零）的資料結構，並且可以作為Double Ended Priority Queue，同時求得最小值與最大值。

Divide-and-Conquer Method，將0到R-1的整數分為sqrt(R)個區塊，每個區塊的範圍大小為sqrt(R)，各區塊各自遞迴下去。

換句話說，就是把整數R-1對半切開，成為高位數字和低位數字。高位數字作為索引值，找出對應的陣列格子，遞迴下去以儲存低位數字。跟「Trie」有點像。

搜尋、插入、刪除都是O(loglogR)，空間複雜度O(R)。

其實我們也可以使用Counting Sort來記錄正整數，速度還比vEB Tree快，只不過Counting Sort不能動態求得極值罷了。

struct vEB_Tree { int digit; // R-1的二進位位數 vEB_Tree* lower[1<<(digit/2)]; // sqrt(R)個區塊 };

若要作為Double Ended Priority Queue，則在每個節點加上兩個變數，記錄該子樹目前擁有的數字的大小範圍。

struct vEB_Tree { int digit; vEB_Tree* lower[1<<(digit/2)]; int min, max; // 子樹目前擁有的數字們，最大值與最小值。 };

僅有理論上的價值，沒有實務上的價值。

Treap

Binary Search Tree與Binary Heap進行合體術。

令數字擁有額外的次序，同時具有「排次序」與「求極值」的功能。樹根的次序介於左右子樹，樹根的數字小於等於左右子樹。

具備排名功效的Binary Search Tree，可以代替Treap。

僅有理論上的價值，沒有實務上的價值。

Randomized Binary Search Tree

平行運算的情況下，合併的時間複雜度極低。

僅有理論上的價值，沒有實務上的價值。

Finger Search Tree

我沒有研究。