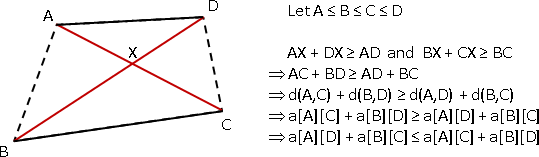sort

「排序」。把一群數字由小到大排好。

排序演算法類型

一、使用循序資料結構，例如array、list，將數字依序放進去，執行排序演算法。

二、使用具備排序功效的資料結構，例如binary search tree、binary heap，將數字整個倒進去、整個倒出來，完成排序。

本文討論第一種類型。第二種類型請見本站文件「binary search tree」。

排序原理

一、對調（比較）。二、放置（索引）。

對調式排序，將小數字往前挪、大數字往後挪。基礎的對調式排序是selection sort。當前最快的對調式排序是pdqsort。

放置式排序，需要額外的記憶體空間來放置數字，但是計算時間遠少於對調式排序。基礎的放置式排序是counting sort。當前最快的放置式排序是radix sort。

英文說法：一、比較式排序演算法comparison-based sorting algorithm、交換排序exchange sort。二、非比較式排序演算法non-comparison-based sorting algorithm、分布排序distribution sort。

等價於數字的東西也可以排序

字元也可以排序。字元就是ASCII碼、就是數字。

指標也可以排序。指標就是記憶體位址、就是數字。

資料也可以排序。只要資料的某個特定欄位是數字，這個欄位稱作鍵值（key）。

等價於數組的東西也可以排序

數組（tuple）也可以排序。其中一種方式：先比較第一維度；如果平手，再比較第二維度；如果又平手，再比較第三維度；以此類推。這個比較方式稱作字典序（lexicographical order）。

字串也可以排序。字串就是一串ASCII碼、就是數組。

英文單字也可以排序。英文單字就是一串字母、字母可以編號、整體宛如數組。英文字典，採用了字典序，排序所有英文單字。

UVa 482

能夠建立全序的東西也可以排序

所有東西均可兩兩比較大小，而且沒有矛盾，稱作全序（total order）。

排序對象沒必要是數字。沒有數字，只有比較；沒有絕對大小，只有相對大小；無法使用放置式排序，只能使用對調式排序。

間接排序

排序會搬動資料，但是大多數時候我們不希望搬動資料。此時可以取出資料的記憶體位址，另外建立指標，對指標進行排序，但是比較對象是指標所指的資料鍵值大小。

也有人使用陣列索引值，道理跟指標相同。

stable

鍵值相同的資料們，原本排在前頭的，排序後仍在前頭；原本排在後頭的，排序後仍在後頭。這稱作「穩定的」排序演算法，鍵值相同、順序不變。

只要是放在陣列的資料，任何一種排序演算法，都可以擴展成穩定的排序演算法。你想到解決方法了嗎？

comparison function（comparator）

對調式排序必須使用「比較函數」。

C標準函式庫的qsort()，其參數cmp就是比較函數。意義是小於，回傳值是int變數，正零負代表< = >。

C++標準函式庫的sort()，其參數cmp就是比較函數。意義是小於，回傳值是bool變數，true false代表< ≮。

C++標準函式庫也有比較函數less()，以便作為參數預設值。

// C int cmp(const void* a, const void* b) // 元素是數字 { return *(int*)a - *(int*)b; } void demo() { int array[5] = {3, 6, 9, -8, 1}; qsort(array, 5, sizeof(int), cmp); } // C++ bool cmp(const int& a, const int& b) // 元素是數字 { return a < b; } void demo() { int array[5] = {3, 6, 9, -8, 1}; sort(array, array+5, cmp); sort(array, array+5); // 第三參數使用預設值less }

sorting network

「排序網路」。兩兩比較的先後次序圖。

每一種對調式排序演算法，都可以畫出排序網路。但是也有例外，例如quicksort的加速技巧：三個中位數的中位數，必須知道數字多寡，才能決定比較對象，此時就無法畫出排序網路。

事情也可以反過來。設計一個新的排序網路，就得到一種新的對調式排序演算法。

排序網路的深度，即是排序演算法的步驟數量。深度下限，已被證明是Ω(NlogN)，不可能更少了。深度最小值，則是NP-complete問題。換句話說，找到一個深度盡量小的排序網路，目前沒有（以後大概也不會有）快速的演算法。

設計排序網路演算法，製造排序演算法，以演算法產生演算法，這件事簡直超酷的。但是很不幸的，這條路很難走。

UVa 1117

排序演算法

               | average   worst     | extra | stable
               | case      case      | space | sort
---------------+---------------------+-------+----
searching sort | O(NR)     O(NR)     | O(N)  | ✓  → my favorite
selection sort | O(NN)     O(NN)     | O(1)  | ✓
---------------+---------------------+-------+----
bubble sort    | O(NN)     O(NN)     | O(1)  | ✓
gnome sort     | O(NN)     O(NN)     | O(1)  | ✓    best
insertion sort | O(NN)     O(NN)     | O(1)  | ✓    stable
Shell sort     | O(NN)     O(NN)     | O(1)  |      comparison-
merge sort     | O(NlogN)  O(NlogN)  | O(N)  | ✓    based
Timsort        | O(NlogN)  O(NlogN)  | O(N)  | ✓  → sort
---------------+---------------------+-------+----
heapsort       | O(NlogN)  O(NlogN)  | O(1)  |
splaysort      | O(NlogN)  O(NlogN)  | O(1)  |
---------------+---------------------+-------+----
quicksort      | O(NlogN)  O(NN)     | O(N)  |      best
introsort      | O(NlogN)  O(NlogN)  | O(N)  |      comparison-
blockquicksort | O(NlogN)  O(NlogN)  | O(N)  |      based
pdqsort        | O(NlogN)  O(NlogN)  | O(N)  |    → sort
---------------+---------------------+-------+---- 
counting sort  | O(N+R)    O(N+R)    | O(R)  | ✓    best
radix sort     | O((N+β)D) O((N+β)D) | O(β)  | ✓  → sort
---------------+---------------------+-------+----
bucket sort    | O(N+β)    O((N+β)D) | O(βD) | ✓
flashsort      | O(N+β)    O((N+β)D) | O(βD) | ✓    best
samplesort     | O(NlogN)  O(NN)     | O(N)  | ✓    parallel
IPS⁴o          | O(NlogN)  O(NN)     | O(N)  | ✓  → sort
---------------+---------------------+-------+----
sleep sort     | O(N+R)    O(N+R)    | O(N)  | ✓  → best of
                                                    the best

N: input size
R: input range
β: radix / bucket count       (β = 2, generally speaking)
D: digits / recursion depth   (D = logᵦR) (R = βᴰ)

Searching Sort

搜尋排序。依序枚舉每一個整數，看看陣列裡頭有沒有。

令最小值是A，最大值是B，從最小值到最大值有R = B-A+1個整數。時間複雜度O(RN)。

void searching_sort(int array[], int N) { int minimum = INT_MAX; int maximum = INT_MIN; for (int i=0; i<N; ++i) { minimum = min(minimum, array[i]); maximum = max(maximum, array[i]); } for (int n=minimum; n<=maximum; ++n) { // 看看陣列裡面有沒有 for (int i=0; i<N; ++i) if (array[i] == n) cout << n; } }

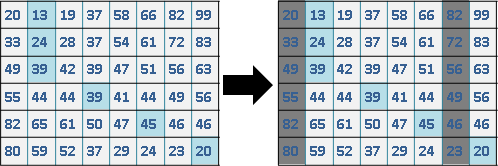
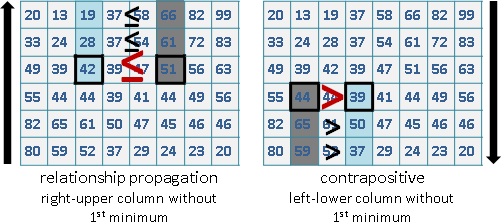
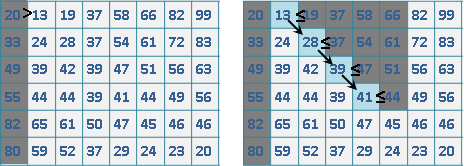
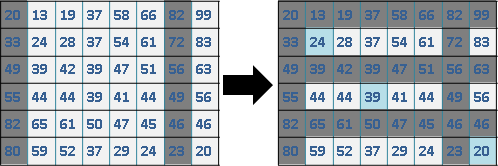
selection sort

選擇排序。掃描一遍所有數字，找到最小值，挪至陣列左端。遞迴處理尚未排序的N-1個數字。

void selection_sort(int array[], int N) { for (int i=0; i<N; ++i) // N改為N-1更精準 { // 從尚未排序的數字當中，找出最小的數字。 // （它也是全部數字當中第i小的數字。） int min_index = i; for (int j=i+1; j<N; ++j) if (array[j] < array[min_index]) min_index = j; // 把第i小的數字，放在第i個位置。 swap(array[i], array[min_index]); } }

bubble sort

氣泡排序。由左到右，相鄰兩兩比較，較大者往右挪，最後最大值會出現在陣列右端。遞迴處理尚未排序的N-1個數字。

void bubble_sort(int array[], int N) { for (int i=0; i<N; ++i) // N改為N-1更精準 for (int j=0; j<N-i-1; ++j) if (array[j] > array[j+1]) swap(array[j], array[j+1]); }

gnome sort

地精排序。bubble sort加強版。調整兩兩比較的先後次序。

特色是程式碼只有一個迴圈，結構簡單。

void gnome_sort(int array[], int N) { for (int i=0; i<N; ) if (i == 0 || array[i-1] < array[i]) i++; else { swap(array[i-1], array[i]); i--; } }

insertion sort

插入排序。由左到右，逐一把數字插入到目前已排序的陣列當中。將大量數字往右挪，以騰出空間插入數字。

資料結構如果是array，可以使用binary search快速找到插入點；但是很不幸的，插入時還是要挪動整塊記憶體。

資料結構如果是list，就無法使用binary search得到插入點；但是很幸運地，插入時不必挪動整塊記憶體。

void insertion_sort(int array[], int N) { for (int i=1; i<N; ++i) { int pivot = array[i]; int j; for (j=i; j>0; --j) if (pivot < array[j-1]) array[j] = array[j-1]; // 往右挪 else break; array[j] = pivot; // 插入 } }

UVa 10107

Shell sort

Shell是作者姓名。insertion sort加強版。

scaling method。固定間隔取得數字作為一組，各組各自做insertion sort；間隔大小減半，重複上述動作。

特色是往右挪的總次數變少了。

void shell_sort(int array[], int N) { for (int gap = N/2; gap > 0; gap /= 2) for (int i = gap; i < N; ++i) for (int j = i-gap; j >= 0 && array[j] > array[j+gap]; j -= gap) swap(array[j], array[j+gap]); }

merge sort

合併排序。divide-and-conquer method。分兩半、分別排序、合併。

可以直接使用C++標準函式庫的stable_sort()。

http://www.rosettacode.org/wiki/Sorting_algorithms/Merge_sort#C

UVa 10810

Timsort

Tim是作者姓名。merge sort加強版。

合併時，若數字大小順序交錯，則適合原本方式，步步前進；若數字大小順序連貫，則適合binary search，大步邁進。

對於短區間，交錯機會少，連貫機會大，於是改成大步邁進。

分水嶺通常設定成64，沒有科學根據。

實務上速度最快的stable的對調式排序演算法。

heapsort

堆積排序。陣列可以當作二元樹。陣列可以當作binary heap。逐一把數字放入binary heap，達到排序功效。

splaysort

伸展排序。陣列可以當作二元樹。陣列可以當作splay tree。逐一把數字放入splay tree，達到排序功效。

quicksort

快速排序。divide-and-conquer method。選定pivot，挪到陣列邊緣，然後把陣列分成大的一邊和小的一邊，兩邊分別排序。

任選一個數字當作pivot，排序結果皆正確。想讓quicksort達到最佳效率，就讓每次選中的pivot，每次都把陣列分成兩等份，如此一來時間複雜度是O(NlogN)。幸運的是，即便把陣列分成數量懸殊的兩半，即便是1000000:1，只要是固定比例，時間複雜度還是O(NlogN)。但是這種事帶點運氣成份。

固定選擇最後一個數字當作pivot，也有機會把陣列分成兩等份。然而這卻產生一個古怪現象：遇到已經排序的陣列，每次都把陣列分成(N-1):1，時間複雜度變成O(N²)，超級慢。quicksort有時快、有時慢；遇到幾乎排序好的陣列，更是慢到吐血。

為了避免這種情況，可以每次都用亂數選擇pivot，如此一來比較不容易出現上述古怪現象。然而這又衍生一個難纏問題：只是做個排序，卻還得載入亂數模組，耗損系統資源、拖慢系統速度，帶來了新的壞處。

最後大家捨棄亂數，轉而構思一些小技巧，讓pivot儘可能把陣列分成兩等分。例如Java的quicksort，把陣列切成前中後三段，拿這三段中央的數字，三個數字的中位數當作pivot。這便是一個簡單實用的小技巧。

// 蠟燭兩頭燒 void quicksort(int array[], int left, int right) { if (left >= right) return; int i = left, j = right; int k = (left + right) / 2; // 可以隨便選 int pivot = array[k]; while (true) { // 小於等於改成小於，就不必偵測陣列邊界。 while (array[i] < pivot) i++; while (array[j] > pivot) j--; if (i >= j) return; // 代價：等於pivot的數字，一直做交換。 swap(array[i], array[j]); i++; j--; } // 代價：array[i]不一定就是pivot。 quicksort(array, left, j); quicksort(array, i, right); } // 蠟燭燒一頭 void quicksort(int array[], int left, int right) { if (left >= right) return; int k = (left + right) / 2; // 可以隨便選 int pivot = array[k]; // 這行可省略 swap(array[k], array[right]); // pivot挪到最右端 int i = left, j = left; for (; j < right; ++j) if (array[j] <= pivot) // pivot就是array[right] if (i < j) // 這行可省略 swap(array[i++], array[j]); if (i < right) // 這行可省略 swap(array[i], array[right]); // right就是j quicksort(array, left, i-1); quicksort(array, i+1, right); } // stackless quicksort，數字為任意數。 https://github.com/yuhanlyu/Snippets/blob/master/sort/quickstackless.c

UVa 755

© 2010 tkcn. All rights reserved.

introsort

內排序。quicksort加強版。遞迴分割陣列，區間越來越短，數字也幾乎排序好了。對於幾乎已經排序好的短區間，quicksort慢到吐血。此時改用heapsort，強硬地壓低最差時間複雜度。

分水嶺通常設定成logN² = 2logN，N是陣列長度。

可以直接使用C++標準函式庫的sort()。

BlockQuicksort

分塊快速排序。quicksort加強版。比較大小，避免branch misprediction，改用整數運算。對調數字，避免cache miss，改用分塊搬運。

pattern-defeating quicksort（pdqsort）

破格快速排序。introsort暨BlockQuicksort加強版。比較大小、對調數字，進行細部改良。盡量避免使用緩慢的heapsort。

實務上速度最快的對調式排序演算法。

counting sort

計數排序。全部數字，依其數值，放到相符位置。由小到大讀取各個位置的數字。只能處理整數。

void counting_sort(int array[], int N) { // 歸類並計數 int count[10000] = {0}; for (int i=0; i<N; ++i) count[ array[i] ]++; // 索引值大小順序，正是數字大小順序。 for (int i=0, k=0; k<N; ++i) while (count[i]--) array[k++] = i; }

UVa 484 11462

radix sort

基數排序。scaling method。低位數到高位數，每個位數依序作為鍵值，總共做D回合counting sort，D為位數大小。

二進位數字，基數β = 2，位數D = logᵦR。實務上取基數β = 256 = 2⁸，記憶體剛好是1 byte = 8 bit。

也能處理二補數。仔細判讀正負號位置。

也能處理浮點數。仔細判讀正負號位置、次方值位置。

實務上速度最快的排序演算法。

https://www.zhihu.com/question/366772394/answer/1012755081

bucket sort

桶排序。divide-and-conquer method。自訂桶子數量β、自訂桶子區間[a₀,a₁)到[aᵦ₋₁,aᵦ)。每個數字放到相符桶子。各個桶子各自排序。由小到大讀取各個桶子的數字。可以處理非整數。

桶子區間，習慣遞迴等分。數字範圍，除以桶子數量，作為桶子區間寬度。每個數字經由除法運算、取整運算，求得相符桶子編號。

void bucket_sort(vector<float>& array, float a0, float range = FLT_MAX) { if (array.size() < 2) return; if (range <= FLT_MIN) return; static const int β = 10; // 桶子數量 range /= β; // 桶子區間寬度 if (range < FLT_MIN) range = FLT_MIN; // 每個數字放到相符桶子 vector<float> bucket[β]; for (float n: array) { int i = floor((n - a0) / range); bucket[i].push_back(n); } // 各個桶子各自排序 for (int i=0; i<β; ++i) bucket_sort(bucket[i], a0 + range * i, range); // 索引值大小順序，正是數字大小順序。 for (int i=0, k=0; i<β; ++i) for (float n: bucket[i]) array[k++] = n; }

flashsort

閃排序。bucket sort加強版。預先求得最小值、最大值，作為數字範圍。最大值減最小值，除以桶子數量，作為桶子區間寬度。

samplesort

抽樣排序。bucket sort加強版。隨機抽樣，作為桶子區間。

可以視作quicksort的通例。大量pivot，將陣列分成多段。

in-place parallel super scalar samplesort（IPS⁴o）

原地平行超純量抽樣排序。samplesort平行化版本。

in-place：額外記憶體空間為O(1)，甚至不需要額外記憶體空間。
parallel：多個中央處理器。此處是指，各桶各自排序。
superscalar：中央處理器，整合處理多個指令。此處是指，整合處理比較與交換。
cache-efficient：記憶體區塊，鮮少反覆載入。此處是指，比較集中在同一區塊。
branch-prediction：if判斷結果，經常預測成功。此處是指，比較結果經常一致。

平行計算的情況下，實務上速度最快的對調式排序演算法。

sleep sort

睡眠排序。源自網路論壇4chan。

延遲輸出，延遲時間是數字大小。數字越小，輸出越早。

實務上最適合拿來裝逼的排序演算法。

https://rosettacode.org/wiki/Sorting_algorithms/Sleep_sort#C.2B.2B

search

「搜尋」。找出一個數字的位置。

search in array: sequential search

循序搜尋。依序看一遍。時間複雜度O(N)。

search in sorted array: binary search

二元搜尋。divide-and-conquer method。已排序陣列，對半分成兩邊，遞迴搜尋其中一邊。時間複雜度O(logN)。

經典應用：資料恰有兩種性質，明顯地分做兩邊，可用binary search找到分界之處。

int binary_search(int array[], int left, int right, int key) { while (left <= right) { // int mid = (left + right) / 2; int mid = left + right / 2; // 避免溢位 if (array[mid] < key) left = mid + 1; else if (array[mid] > key) right = mid - 1; else if (array[mid] == key) return mid; } // return -1; // 找不到 return left; // 如果找不到，就回傳稍大一點的數值位置。 }

UVa 10611 10077

search in sorted array: interpolation search

內插搜尋。binary search加強版。根據陣列左右兩端數字大小，一次內插，作為分割位置。

int interpolation_search(int array[], int left, int right, int key) { while (left <= right) { int mid = low + (key - array[left]) * (right - left) / (array[right] - array[left]); // 一次內插 if (array[mid] < key) left = mid + 1; else if (array[mid] > key) right = mid - 1; else if (array[mid] == key) return mid; } return left; }

search in sorted unbound array: doubling search

倍增搜尋。主持人心中有一正整數，我們可以一直猜他心中的正整數，但是他只會回答「太高」或「太低」或「正確」。請問要怎麼猜可以最快猜到他心中的正整數呢？

有個類似的團康遊戲叫做「終極密碼」，常常在綜藝節目出現。「終極密碼」的規則比較不一樣，數字範圍通常只有1到100，而且是很多個人輪流猜，越晚猜出來越好。這裡的猜數字遊戲，數字範圍是1到無限大，只有一個人猜，越早猜出來越好。

言歸正傳。從1開始一個一個往上猜，實在太慢了。比較快的猜法，是將問題分成兩個步驟，第一個步驟是先確定範圍，第二個步驟再來縮小範圍。

確定範圍：可以從1、2、4、8、……這個順序去猜。如果主持人不斷回答太低，我們就不斷往大數字猜，一直到主持人回答太高為止。如果主持人心中的正整數為N，則可以用O(logN)的時間得到一個合理的範圍，N會落在(2ᵏ⁻¹, 2ᵏ]之間。

縮小範圍：可以使用binary search！從(2ᵏ⁻¹, 2ᵏ]之間找出正確的正整數，只需O(logN)時間。

二元搜尋和倍增搜尋相互對立，前者除以二、後者乘以二。

search in sorted arrays: fractional cascading

search in sorted matrix: saddleback search

鞍背搜尋。二維矩陣裡的數字經過排序，往右、往下都呈現嚴格遞增，此時有個很巧妙的搜尋方式，時間複雜度O(X+Y)，X與Y分別為矩陣的長與寬。

首先在腦中將矩陣的數字切割為大於n的一邊（右下）與不大於n的一邊（左上）。現在我們所要作的，便是遊走於大與小的邊緣來尋找n！從矩陣的右上角開始，嘗試走到左下角，若走到了大於n的一邊，就立即往不大於n的另一邊移動，反之亦同。

各位可以想想當找到目標數字時，應該往左還是往下走好？當矩陣數字是非嚴格遞增的時候會產生什麼問題？

UVa 12192

select

「選擇」。找到特定名次的數字，例如第k小的數字。

最簡單的方式就是先排序、再搜尋。以下探討更快的方法。

UVa 10041 10107 11875

select in array: quickselect

quicksort只遞迴其中一邊。平均時間複雜度O(N)，最差時間複雜度O(N²)。

可以進化成introselect、pdqselect。最差時間複雜度O(N)。

可以直接使用C++標準函式庫的nth_element()，但是細節不盡相同。

select in array: median-of-medians algorithm

找到中位數們的中位數（中中數），將數字分成大的一邊和小的一邊，遞迴找其中一邊。時間複雜度O(N)，但是不實用。

1. 五個五個分堆，最後一堆可以沒有滿。

   第一堆 ● ● ● ● ●
   第二堆 ● ● ● ● ●
   第三堆 ● ● ● ● ●
   第四堆 ● ● ● ● ●
   第五堆 ● ● ● ● ●
   第六堆 ● ● ●

2. 每堆各自排序。然後求出每堆的中位數 ○。

      小  →  大
   ↑  ● ● ○ ● ●
   沒 ● ● ○ ● ●
   有 ● ● ○ ● ●
   順 ● ● ○ ● ●
   序 ● ● ○ ● ●
   ↓    ● ○ ●     ← 最後一堆對齊一下比較好看

3. 求出中位數們的中位數 x。遞迴套用此演算法求得 x。

      小  →  大
   ↑  ● ● ○ ● ●
   沒 ● ● ○ ● ●
   有 ● ● ○ ● ●
   順 ● ● ○ ● ●
   序 ● ● x ● ●   ← 中位數可能在任何一個地方
   ↓    ● ○ ●

4. 將全部的數字分成兩邊，一邊小於 x ，一邊大於等於 x。

         小於 x ←|   |→ 大於等於 x
   ... ● ● ● ● ● ● x ● ● ● ● ● ● ● ● ...

5. 看看 k 是在哪一邊。遞迴下去找出答案。

時間複雜度証明

          小  →  大
   第一堆 ● ● ○ ● ●
   第二堆 ● ● ○ ● ●
   第三堆 ● ● ○ ● ●
   第四堆 ● ● ○ ● ●
   第五堆 ● ● x ● ●
   第六堆   ● ○ ●

依照中位數們的大小，重新排列每一堆。

              小  →  大
   第四堆  中 ● ● ○ ● ●
   第二堆  位 ● ● ○ ● ●
   第五堆  數 ● ● x ● ●   ← 中位數 x 變成排在中間
   第一堆  小 ● ● ○ ● ●
   第三堆  ↓  ● ● ○ ● ●
   第六堆  大   ● ○ ●

觀察一定小於等於x的數、一定大於等於x的數。

   一定小於    一定大於
   等於x的數   等於x的數
   ◊ ◊ ◊ ● ●   ● ● ○ ● ●
   ◊ ◊ ◊ ● ●   ● ● ○ ● ●
   ◊ ◊ x ● ●   ● ● x ◊ ◊
   ● ● ○ ● ●   ● ● ◊ ◊ ◊
   ● ● ○ ● ●   ● ● ◊ ◊ ◊
     ● ○ ●       ● ◊ ◊

推得「小於等於 x 的數至少有 3n/10 - 6 個。大於 x 的數至多有 7n/10 + 6 個。」
推得「大於等於 x 的數至少有 3n/10 - 6 個。小於 x 的數至多有 7n/10 + 6 個。」

  至多7n/10 + 6         差不多至多7n/10 + 6
         小於 x ←|   |→ 大於等於 x
   ... ● ● ● ● ● ● x ● ● ● ● ● ● ● ● ...

分兩邊後，
小於的那一邊至多有 7n/10 + 6 個，
大於等於的那一邊差不多至多有 7n/10 + 6 個。
遞迴下去，總時間複雜度 O(n)。

select in array: Floyd–Rivest algorithm

據說是實務上速度最快的選擇演算法。

select in sorted array

O(1)。

select in sorted arrays

找到中中數，然後每列皆實施binary search，最後所有數字分為大的一邊和小的一邊，遞迴找其中一邊。每回合至少削減一半的列的一半。每列各自建立首尾索引值，記錄剩下的數字。

每回合需時O(XlogY)，總共O(logY)回合，時間複雜度O(XlogYlogY)。X是陣列數量，Y是陣列長度。

簡單來說，此演算法是搜尋中中數、分兩邊、遞迴一邊。

select in sorted arrays

找到X個中位數，然後找到最大中位數、最小中位數。每回合削減最大中位數的右半或最小中位數的左半。每回合刪除一列的一半，總共O(XlogY)回合。

以二元搜尋樹儲存X個中位數，每回合可以快速找到最大中位數、最小中位數。總共操作O(XlogY)次，每次操作O(logX)，時間複雜度O(XlogXlogY)。X是陣列數量，Y是陣列長度。

select in sorted matrix

切成一列一列，找到中中數。利用saddleback search將矩陣分為大的一邊和小的一邊，遞迴找其中一邊。

每回合需時O(N)，總共O(logN)回合，時間複雜度O(NlogN)。

select in sorted matrix

divide-and-conquer method。O(N)。

extremum

「極值」。細分為最大值maximum、最小值minimum。

找到極值本身，甚至找到出現次數、出現位置。

循序搜尋。時間複雜度O(N)，額外的空間複雜度O(1)。

mode

「眾數」。出現最多次的數字。

先排序再搜尋。採用對調式排序，例如merge sort，時間複雜度O(NlogN)，額外的空間複雜度O(1)。採用放置式排序，例如counting sort，時間複雜度O(N+R)，額外的空間複雜度O(R)。

longest plateau

一串數字當中，連續出現最多次的數字，找到出現次數。

int longest_plateau(int a[], int n) { if (n == 0) return 0; int counter = 1; int length = 1; for (int i=1; i<n; i++) { if (a[i] == a[i-1]) { counter++; length = max(length, counter); } else counter = 1; } return length; }

已排序陣列，有更簡單的做法。

int longest_plateau(int a[], int n) { if (n == 0) return 0; int length = 1; for (int i=1; i<n; i++) if (a[i] == a[i-length]) length++; return length; }

majority

「過半數」。過半的數字。

找到其中一個過半數。時間複雜度O(N)，額外的空間複雜度O(1)。

// Boyer–Moore Majority vote algorithm int find_majority(int a[], int n) { int majority = a[0], counter = 0; for (int i=0; i<n; i++) if (counter == 0) majority = i, counter = 1; else if (a[i] == majority) counter++; else counter--; counter = 0; for (int i=0; i<n; i++) if (a[i] == majority) counter++; if (counter < (n+1)/2) return -1; return counter; }

distinct count

相異數字個數。

先排序再搜尋。時間複雜度O(NlogN)或O(N+R)。

近似演算法是「Flajolet–Martin sketch」和「HyperLogLog」。

maximum gap

一串數字，排序之後，相鄰兩數的差值，其中最大的差值稱作「最大間隔」。可能同時有許多個「最大間隔」。

flashsort可以找出所有最大間隔。時間複雜度O(N)。

一、找到最大值max、最小值min。
二、建立N-1個桶，每個桶的範圍大小是 D = (max-min)/(N-1)。
三、除了最大值、最小值，
　　剩下的N-2個數字通通塞入桶，
　　數字 x 塞到 floor[(x-min)/D]。
四、N-1個桶，N-2個數字，必有空桶。
　　最大間隔的兩數必定跨過空桶，最大間隔大於D。
　　最大間隔的兩數不在同一個桶。
五、找到每個桶的最大值bucket[i].max、最小值bucket[i].min。
六、刪除空桶，重新編號。
　　max { bucket[i+1].min - bucket[i].max } 即是最大間隔。

minimum gap

先排序再搜尋。時間複雜度O(NlogN)或O(N+R)。【尚待確認】

X+Y

窮舉法。O(N²)。

Fourier transform。O(N + RlogR)。

sort in X+Y

先窮舉，再排序。O(N²logN²) = O(N²logN)。

先排序，再N-way merge。O(N²logN)。

Fourier transform。O(N + RlogR)。

search in X+Y

先排序。想像矩陣add[i][j] = a[i] + b[j]，已排序矩陣的搜尋。O(NlogN)。

select in X+Y

先排序。想像矩陣add[i][j] = a[i] + b[j]，已排序矩陣的選擇。O(NlogN)。

search in 2D X+Y

找y/x。最差O(Nlog²N)，平均Θ(NlogN)。

select in 2D X+Y

找y/x。Θ(NlogN)。

extremum in 2D X+Y

找y/x。必在凸包上。Θ(NlogN)。

all row minimums

以下介紹三個特殊矩陣，以及其「每一個橫條（直條）的最小值」的演算法。

Monge matrix ⇒ totally monotone matrix ⇒ monotone matrix。從特例到通例，限制從強到弱，數量從少到多，演算法從快到慢。

Monge matrix (concave)
[standard form] ↖ + ↘ ≤ ↗ + ↙      主對角線和，小於等於次對角線和
     [row form] ↘ - ↙ ≤ ↗ - ↖      橫條各處斜率，往上遞增
  [column form] ↘ - ↗ ≤ ↙ - ↖      直條各處斜率，往左遞增

totally monotone matrix
   [row type] if ↙ ≤ ↘ then ↖ ≤ ↗  橫條小於等於關係，往上遞增
[column type] if ↗ ≤ ↘ then ↖ ≤ ↙  直條小於等於關係，往左遞增

monotone matrix
   [row type] argmin ⤷             橫條最小值位置，往下遞增
[column type] argmin ⤵             直條最小值位置，往右遞增

Monge matrix

矩陣當中所有田字四個格子皆滿足不等式：↖ + ↘ ≤ ↗ + ↙。

不等式分成凹凸兩種，大小相反、性質顛倒。以下以凹為主。

concave Monge matrix: a[i][j] + a[i+1][j+1] ≤ a[i][j+1] + a[i+1][j]
 convex Monge matrix: a[i][j] + a[i+1][j+1] ≥ a[i][j+1] + a[i+1][j]

另一種等價的寫法：所有子矩形的四個端點皆滿足不等式。

a[i₁][j₁] + a[i₂][j₂] ≤ a[i₁][j₂] + a[i₂][j₁] when i₁ < i₂ and j₁ < j₂

移項一下，得到橫條（直條）斜率遞減的形式。彷彿凹函數。

Monge matrix乘以非負倍率，仍是Monge matrix。

Monge matrix相加，仍是Monge matrix。

Monge matrix has "non-negative linearity":
(1) X is Monge matrix, k ≥ 0   ⇒ kX is Monge matrix
(2) X and Y are Monge matrices ⇒ X+Y is Monge matrix

Monge matrix刪除橫條（直條），仍是Monge matrix。

Monge matrix橫條（直條）加上同一數，仍是Monge matrix。

symmetric Monge matrix = Supnick matrix。恰好沿著主對角線對稱。

convex/concave Monge matrix = submodular/supermodular function。矩陣行列索引值，視作區間左右邊界。

舉個實際範例。例如二維平面上，凸四邊形上下邊相加 ≤ 兩條對角線相加，距離雙向均等，符合Supnick matrix不等式。

Supnick matrix的延伸意義是：不交換最好。例如尋找最佳排列的問題travelling salesman problem、assignment problem，若滿足Supnick matrix，則有高速演算法。

totally monotone matrix

分成凹凸兩種，又細分成橫直兩種，共四種。以下以凹為主。

橫條（直條）一旦出現≤，上方（左方）也都是≤。

concave row version:    if ↙ ≤ ↘ then ↖ ≤ ↗
concave column version: if ↗ ≤ ↘ then ↖ ≤ ↙

自然界難以見到totally monotone matrix，其定義是計算學家故意設計的，是從monge matrix的不等式所推導出來的性質。

Monge matrix ⇒ totally monotone matrix的證明：橫條（直條）斜率遞減的形式當中，若左式非負，則右式也非負。

monotone matrix

分成凹凸兩種，又細分成橫直兩種，共四種。以下以凹為主。

每個橫條（直條）的第一個最小值位置，往右（往下）遞增。最小值可能有許多個，所謂的第一個是指索引值最小者。

row version:    argmin r₀ ≤ argmin r₁ ≤ argmin r₂ ≤ ... 
column version: argmin c₀ ≤ argmin c₁ ≤ argmin c₂ ≤ ... 

自然界難以見到monotone matrix，其定義是計算學家故意設計的，是從totally monotone matrix的不等式所推導出來的性質。

totally monotone matrix ⇒ monotone matrix的證明：因為上方橫條（左方直條）小於等於關係不變，所以最小值位置只可能一樣、或者更往左（更往上）。

尋找monotone matrix的每個橫條（直條）的第一個最小值

分治法。找到中央橫條的最小值，然後左上矩陣與右下矩陣，分別遞迴求解。時間複雜度O(YlogX)。

const int X = 6; const int Y = 8; int a[X][Y]; // monotone matrix int min_index[X]; // 記錄最小值位置 // call minimum(0, X-1, 0, Y-1) at first void minimum(int i1, int i2, int j1, int j2) { if (i1 > i2) return; /* divide：找到中央橫條的最小值 */ int i = (i1 + i2) / 2, j; // 中央橫條、最小值位置 int min = 1e9; for (j=j1; j<=j2; ++j) if (a[i][j] < min) { min = a[i][j]; min_index[i] = j; } /* conquer：左上矩陣與右下矩陣，分別遞迴求解。*/ minimum(i1, i-1, j1, j); minimum(i+1, i2, j, j2); }

尋找totally monotone matrix的每個橫條（直條）的第一個最小值

限制更強了，擁有更快的演算法。分治法，三個步驟。

一、刪除多餘直條，將X×Y矩陣變成X×X方陣：

把矩陣裡面每一個橫條的第一個最小值圈出來。目標是：砍掉不含第一個最小值的直條。砍到變成方陣即可，不必趕盡殺絕。

任意橫條上面，任取兩個數字a[i][j₁] a[i][j₂]，比較大小。如果a[i][j₁] ≤ a[i][j₂]，表示右邊數字以上，皆不含第一個最小值。如果a[i][j₁] > a[i][j₂]，表示左邊數字以下，皆不含第一個最小值。

沿對角線前進，與右邊數字比較大小。如果a[i][i] ≤ a[i][i+1]，那麼姑且繼續前進，累積無效區域，使得上三角矩陣都是無效區域。如果a[i][i] > a[i][i+1]，那麼對角線當前數字以下是無效區域，恰好跟先前的無效區域，湊出一整個直條，得以刪除。

二、遞迴求解，以找到偶數橫條的最小值：

偶數橫條合併成一個X/2×X矩陣，遞迴求解。

三、內插夾擠，以找到奇數橫條的最小值：

把矩陣裡面每一個橫條的第一個最小值圈出來，從上往下看，第一個最小值的位置從左往右遞增。用偶數橫條的最小值位置，夾擠出奇數橫條最小值的可能位置，然後窮舉搜尋就行了。

此演算法稱作SMAWK algorithm。時間複雜度O(X+Y)。

const int X = 6; const int Y = 8; int a[X][Y]; // totally monotone matrix void reduce() // 刪除多餘直條 { int i = 0; // 直條編號，從0到Y-1。 while (a尚未成為方陣就繼續) { // a[1:i][i+1]右上直條不含第一個最小值。 if (a[i][i] <= a[i][i+1] && i+1 < Y-1) { i++; // 繼續沿對角線前進，累積無效區域 } // a[1:i][i+1]恰是矩陣最右端直條，恰是一整個無效直條。 else if (a[i][i] <= a[i][i+1] && i+1 == Y-1) { 砍第i+1直條; if (i > 0) i--; } // a[i:n][i]左下直條不含第一個最小值。 else if (a[i][i] > a[i][i+1]) { 砍第i直條; // 恰好湊成一整個無效直條。 if (i > 0) i--; } } }

尋找Monge matrix的每個橫條（直條）的第一個最小值

限制更強了，理應有更簡易的演算法，但是似乎沒人研究？

可以直接使用上述兩個演算法。

UVa 12311