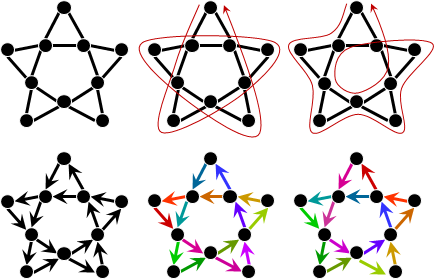
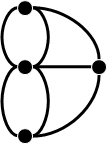
Hamilton tour（Hamilton cycle）（spanning cycle）

每一點剛好經過一次的路線，起點和終點相同。可能有許多種，也可能不存在。

Hamilton path（spanning path）

每一點剛好經過一次的路線，起點和終點不相同。可能有許多種，也可能不存在。

travelling salesman problem

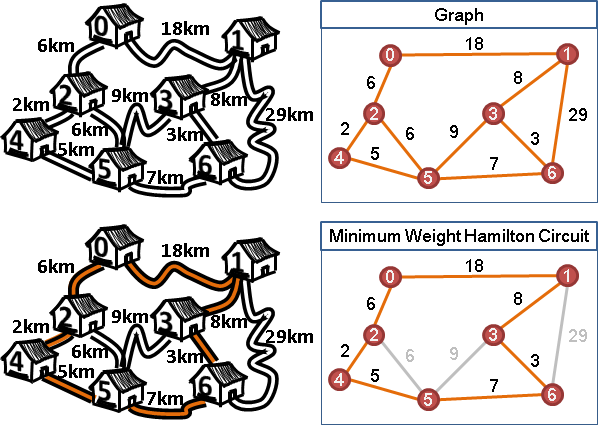
一個周遊各國的商人，他想去所有不同的城市買賣東西。商人打算從其中一個城市出發，各個地方剛好經過一次、只能經過一次，回到原城市。請規劃出距離最短的路線，以及算出距離。

有時候走回頭路會比較快，然而商人就是不想這麼做。

這個問題其實就是找到權重最小的Hamilton tour。

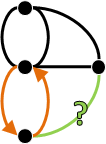
找到一個Hamilton tour

NP-complete問題，目前尚未出現有效率的演算法。

採用backtracking，窮舉所有地點排列方式，一一確認，時間複雜度O(V!)。採用dynamic programming降為O(2ⱽ V²)。

const int V = 9; // 點數 bool adj[V][V]; // adjacency matrix bool visit[V]; // 目前已經經過的點 int solution[V]; // Hamilton tour void backtrack(int n) { if (n == V) { // 判斷最後一點到第一點是否頭尾銜接 int a = solution[V-1]; int b = solution[0]; if (adj[a][b]) { // 找到一組解 for (int i=0; i<V; ++i) cout << solution[i]; cout << '\n'; } return; } int a = solution[n-1]; for (int b=0; b<V; ++b) if (adj[a][b] && !visit[b]) { visit[b] = true; solution[n] = b; backtrack(n+1); visit[b] = false; } } void HamiltonTour() { visit[0] = true; // Hamilton tour從哪一點開始都行， solution[0] = 0; // 直接將第一個點設定為第0點， backtrack(1); // 然後從下一個點開始backtrack。 }

並不是所有的圖都難以找到Hamilton tour。連結性質比較強的圖，就容易找到Hamilton tour，例如Ore's theorem與knight's tour。

Ore's theorem

一張無向圖，不相鄰的兩點，其邊數相加皆大於等於V，則必定存在Hamilton tour。找到一個Hamilton tour，時間複雜度O(V²)。

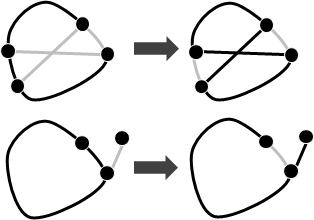
一、隨機走出一條路徑，盡量長：
　　如果是路徑，則從步驟二開始；如果恰好形成環，則從步驟三開始。
　　輪流進行步驟二與步驟三，直到形成Hamilton tour為止。
　　如果無法操作表示此無向圖無Hamilton tour。

二、路徑變環（總共增加一條邊）：
　　路徑(p1, p2, ..., pk)。
　　路徑上找到一條邊(pi, pi+1)，同時原圖又有邊(pi, pk)與邊(pi+1, p1)，
　　去掉邊(pi, pi+1)、接上邊(pi, pk)與邊(pi+1, p1)，
　　形成環(p1, p2, ..., pi, pk, pk-1, ..., pi+1, p1)。

三、環變路徑（總共增加一個點）：
　　環(p1, p2, ..., pk, p1)。
　　環上找到一點pi，同時原圖又有邊(pi, q)連到環外一點q，
　　就去掉邊(pi, pi+1)、接上邊(pi, q)，
　　形成路徑(q, pi, pi-1, ..., p2, p1, pk, pk-1, ..., pi+1)。
　　或者去掉邊(pi, pi-1)、接上邊(pi, q)，
　　形成路徑(q, pi, pi+1, ..., pk-1, pk, p1, p2, ..., pi-1)。

UVa 775

knight's tour

一隻騎士放在西洋棋盤上。讓騎士一筆劃走過棋盤上六十四個方格、回到原點。

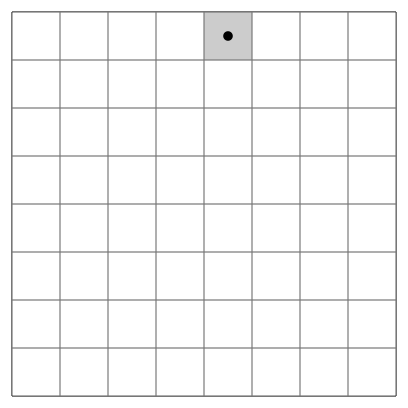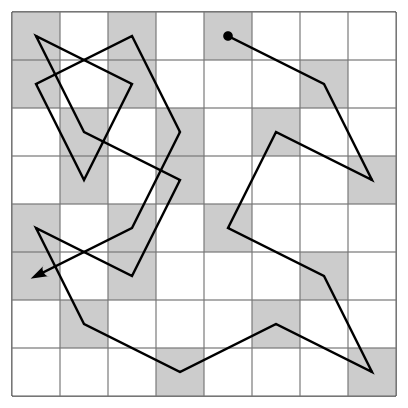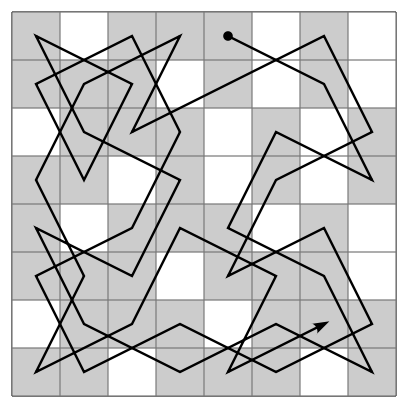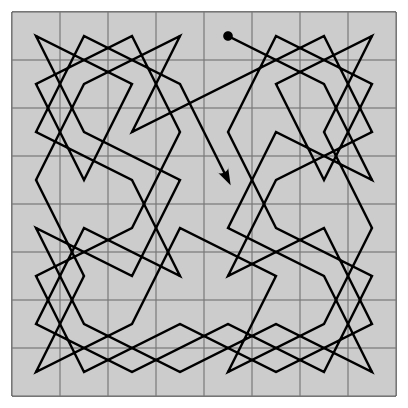
此問題是Hamilton tour的特例。給定N×M的棋盤，找到一個knight's tour，時間複雜度O(NM)。

另一種懶惰的方式是Warnsdorff's rule：每一步都走向後續路線最少的格子；如果同時有很多格子，就走向最左邊、最下邊的格子。這個方法有時會出錯。

UVa 10255

車輛路徑問題

給定起點，除了起點以外，每一點剛好經過一次的路線。

一個倉庫（物流中心）、數台貨車（有承載限制）。另外有幾位客戶，分散各處，各自需要某些商品，該如何規劃配送路線、配送車次，使得油耗最少？

seven bridges of Königsberg

「七橋問題」。有一說是當地居民的休閒活動就是遊覽那七座橋，大家都在嘗試找一條可以經過七座橋各一次，然後回到原處的路線。這活動蔚為風潮，許多數學家聽到這個消息後，也致力於解決這個問題，卻都無疾而終。這個問題也傳到了數學家Euler的耳中，最後他想出了一個漂亮的證法。

另外還有一個童話版本：有天國王想召王宮貴族一起出去散散心，遊覽他的庭園。國王他打算從他的城堡出發，看一看他的庭園花草，以及在他庭園裡的七座橋上散散步。然後回到城堡裡去。由於天氣一定很好、陽光一定很強，屆時出發後絕不要在同一座橋上反反覆覆的走來走去，一直曬太陽，看同樣的風景，那多煩悶。

國王於是下令叫他的臣子們好好的規劃一下出遊路線，每一座橋都要參觀到，而且絕不能讓大家走同樣的橋兩次。臣子們想了很久，卻連一條路線都規劃不出來，國王只好召來聰明的數學大臣Euler來解決這個問題。Euler奉旨後，自行在家沒日沒夜的閉關了三天，終於解決了這個問題：他證明出路線不存在！

Euler當然要能向國王解釋路線為何不存在，要不然國王肯定氣得叫人把他吊起來。Euler想到，無論陸地和橋的形狀、距離、位置是如何，要找出合適的遊覽路徑，只跟橋與陸地如何連接有關係。Euler首先把庭園的地圖，簡化成我們在圖論中所看到的「圖」，圓形（點）就是陸地，線（邊）就是橋。Euler發明的這張「圖」包含了充分的連接資訊，他也是第一個使用「圖」來解決問題的數學家。

接著Euler想到，如果每一座橋只能穿過一次，那麼一座橋就成了去而不回的單行道。然後，對圖上的某一個點來看，一旦從某座橋進入了一次，就要從另一座橋走出去一次，而不會一直停留在某個點上——這跟從哪裡走來、怎麼走來、哪裡出去、怎麼出去無關。所以，只要看到有個點有奇數個邊，也就是有塊陸地有奇數座橋，就表示有這塊陸地有一條橋會讓國王走得過去、卻走不出來，此時就得重複走一座橋、或不走這座橋——代表著國王的遊歷路線不存在。

不知道國王後來還有沒有出遊？不過Euler的這個證明過程倒是出名了。數學家們為了紀念Euler的這項貢獻，把一筆劃走過所有邊各一次後恰好回到起點的路線，稱作Euler tour。tour是遊覽的意思。

Euler tour（Euler circuit）（spanning circuit）

每條邊剛好經過一次的路線，起點和終點相同。可能有許多種，也可能不存在。

一張圖存在Euler tour的條件是：

無向圖：每個點都是偶數條邊。連通圖。
有向圖：每個點的出邊與入邊一樣多。連通圖。

Euler path（Euler trail）（spanning trail）

每條邊剛好經過一次的路線。可能有許多種，也可能不存在。

一張圖存在Euler path的條件是：

無向圖：恰有零個點或兩個點是奇數條邊。連通圖。
有向圖：恰有一點，出邊比入邊多一條（作為起點）；
　　　　恰有一點，入邊比出邊多一條（作為終點）；
　　　　其他的點，出邊與入邊一樣多。連通圖。
　或者，每個點的出邊與入邊一樣多（任選兩點作為起點與終點）。連通圖。

無向圖找出一個Euler tour（Hierholzer's algorithm）

一個Euler tour，在某點相交，可以拆成兩個Euler tour。

兩個Euler tour，在某點相接，可以合成一個Euler tour。

大的拆成小的，小的接成大的——自然想到divide-and-conquer method。

圖上隨意走一圈。未及之處，一定是一個或多個Euler tour。

divide ：圖上隨意走一圈。
conquer：其餘部份遞迴下去。
combine：其餘部分的Euler tour們，銜接到隨意走的那一圈。

圖的資料結構為adjacency matrix是O(V² + E)；圖的資料結構為adjacency list是O(V+E)。

int adj[9][9]; // adjacency matrix int degree[9]; // 記錄每個點的邊數 deque<pair<int,int>> edges; // Euler tour經過的邊 // deque<int> vertices; // Euler tour經過的點 bool hierholzer() { memset(degree, 0, sizeof(degree)); int E = 0; // 總邊數 for (int x=0; x<9; ++x) for (int y=x; y<9; ++y) { degree[x] += adj[x][y]; // 累計連到x點的邊數 degree[y] += adj[x][y]; // 累計連到y點的邊數 E += adj[x][y]; // 累計邊數 } for (int i=0; i<9; ++i) // 檢查每個點 if (degree[i] % 2 == 1) // 如果某個點擁有奇數條邊 return false; int s = -1; // 設定起點 for (int i=0; i<9; ++i) if (degree[i] > 0) // 有邊的點當作起點 { s = i; break; } if (s == -1) return true; // 此圖無點 edges.clear(); // vertices.clear(); all_tour(s); // 遞迴亂繞圈圈 // 圖可能不連通，檢查是否走完所有邊。 if (edges.size() != E) return false; // if (vertices.size() != E+1) return false; return true; } // 亂繞一圈，迴圈版本。 deque<pair<int,int>> edges; // 記錄Euler tour經過的邊 // deque<int> vertices; // 記錄Euler tour經過的點 int next(int x) { for (int y=0; y<9; ++y) if (adj[x][y] > 0) return y; return -1; } void one_tour(int s) { // vertices.push_back(s); for (int x = s, y; (y = next(x)) != -1; x = y) { adj[x][y]--; if (x != y) adj[y][x]--; edges.push_back({x, y}); // vertices.push_back(y); } } // 亂繞一圈，遞迴版本。 void one_tour(int x) { // vertices.push_back(x); for (int y=0; y<9; ++y) // 找一條可以走的邊 if (adj[x][y] > 0) { adj[x][y]--; if (x != y) adj[y][x]--; edges.push_back({x, y}); one_tour(y); break; } } // 亂繞圈圈，遞迴版本。O(VE)。 void all_tour(int x) { for (int y=0; y<9; ++y) // 不斷找可以走的邊 if (adj[x][y] > 0) { adj[x][y]--; if (x != y) adj[y][x]--; all_tour(y); edges.push_front({x, y}); // break消失不見 } // vertices.push_front(x); } // 亂繞圈圈，遞迴版本。O(V² + E)。 int current_y[9] = {0}; // 加速至O(V²)的手段 void all_tour(int x) { for (int& y = current_y[x]; y<9; ++y) if (adj[x][y] > 0) { adj[x][y]--; if (x != y) adj[y][x]--; all_tour(y); edges.push_front({x, y}); } // vertices.push_front(x); }

有向圖找出一個Euler tour

每個點的入邊與出邊分開來看，如果入邊與出邊的數量相等，表示有路可走。

除此之外，都與無向圖相同。

混合圖找出一個Euler tour

UVa 117 291 302 10054 10129 10441 10506 10596 10735

中國郵差問題

郵差叔叔走訪每條大街小巷，讓家家戶戶都收到信。

給定一張圖，找出一條環狀路線，圖上每條邊至少經過一次，並且距離最短。

無向圖演算法

1. 先判斷整張圖是否為一個強連通分量，否則無解。
2. 找出圖上所有奇點，一定是偶數個。
3. 找出所有奇點點對之間的最短路徑長度。
4. 把這些奇點做最小權匹配，權重採用剛才算的最短路徑長度。
5. 把匹配邊加在原圖上，再找歐拉環，即得中國郵差路徑之權重。
6. 將匹配邊改成其代表的最短路徑，即得中國郵差路徑。

時間複雜度是六項步驟總和。各條匹配邊所代表的最短路徑，絕對不會重疊。

ICPC 4039

有向圖演算法

1. 先判斷整張圖是否為一個強連通分量，否則無解。
2. 找出圖上所有出邊數不等於入邊數的點。
3. 於上述找到的點，找出所有點對之間的最短路徑長度。
4. 令d(x)為x點出邊與入邊的數量差。
   出邊多於入邊的點x，建立d(x)份，放在X側。
   出邊少於入邊的點y，建立d(y)份，放在Y側。
   最後建立X側到Y側的邊，權重採用剛才算的最短路徑長度。
   算最小權二分匹配。
4. 合理的做法是建立最小權最大流模型：
   把出邊多於入邊的點x，放在X側。拉一條源點到x點的邊，權重為零，容量為d(x)。
   把出邊少於入邊的點y，放在Y側。拉一條y點到匯點的邊，權重為零，容量為d(y)。
   最後建立X側到Y側的邊，權重採用剛才算的最短路徑長度，容量為無限大。
   算最小權最大流。
5. 把匹配邊加在原圖上，再找歐拉環，即得中國郵差路徑之權重。
6. 將匹配邊改成其代表的最短路徑，即得中國郵差路徑。

時間複雜度是六項步驟總和。

簡單來說：minimum cost flow，每條邊容量下限皆為一。