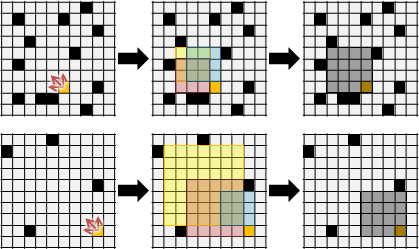
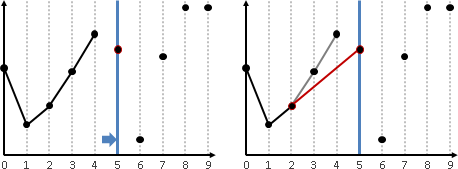
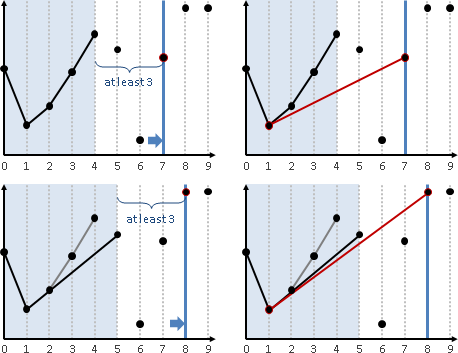
largest empty interval

一條陣列，有些格子已被放上障礙物。最長的、連續的空白格子在哪裡？

length(i) =
 ⎧ 0                , if i < 0                    [exterior]
 ⎪ 0                , if i = 0 and array[i] = 0   [initial state]
 ⎨ 1                , if i = 0 and array[i] = 1   [initial state]
 ⎪ 0                , if i > 0 and array[i] = 0   [computation]
 ⎩ length(i-1) + 1  , if i > 0 and array[i] = 1   [computation]

length(i)：第0格到第i格的連續空白長度。
array[i]：障礙物為0，空白為1。

length(i) =
 ⎰ array[i]                      , if i = 0
 ⎱ array[i] ⋅ (length(i-1) + 1)  , if i > 0

length(i)：第0格到第i格的連續空白長度。
array[i]：障礙物為0，空白為1。

時間複雜度O(N)，空間複雜度O(N)，N為陣列長度。

如果只想計算一個特定問題的答案，空間複雜度O(1)。

程式碼：求出最長空白的長度

int array[10] = { 0, 1, 1, 1, 0, 1, 1, 0, 1, 1 }; int length[10]; void largest_empty_interval() { // [initial states] if (array[0] == 0) length[0] = 0; else length[0] = 1; // [computation] for (int i=1; i<10; i++) if (array[i] == 0) length[i] = 0; else length[i] = length[i-1] + 1; // 輸出結果 int max_length = 0; for (int i=0; i<10; i++) if (length[i] > max_length) max_length = length[i]; cout << "最長空白的長度是" << max_length; }

為了讓程式碼更清爽，把判斷式化作乘法運算。

這個技巧是實務上最佳做法，唯一缺憾是程式碼不直觀。然而這篇文章是教學文章，基本要求是程式碼直觀，所以下文不予採用。

int array[10] = { 0, 1, 1, 1, 0, 1, 1, 0, 1, 1 }; int length[10]; void largest_empty_interval() { // [initial states] length[0] = array[0]; // [computation] for (int i=1; i<10; i++) length[i] = (length[i-1] + 1) * array[i]; // 輸出結果 ...... }

為了讓程式碼更清爽，這裡把array[]、length[]裡面的數值都往右移動一格，如此就可以省略length[0]的程式碼，也避免length[i-1]溢出邊界。

為了讓程式碼更清爽，這裡也把length[]都初始化為0，如此就不必特別處理array[i] == 0的情況了，相當巧妙。

int array[10 + 1] = { 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1 }; int length[10 + 1]; void largest_empty_interval() { // [initial states] memset(length, 0, sizeof(length)); // [computation] for (int i=1; i<=10; i++) if (array[i] == 1) length[i] = length[i-1] + 1; // 輸出結果 ...... }

這兩個技巧是經常使用的的實作技巧，不僅簡化了程式碼的結構，也增加了程式的效率。一定要學會！

程式碼：求出最長空白的位置

void largest_empty_interval() { ...... // 求出所有最長空白的位置 for (int i=1; i<=10; i++) // 從1開始 if (length[i] == max_length) { // 記得減回1 cout << "有一個最長空白的位置是" << "從" << (i - max_length + 1) - 1 << "到" << (i ) - 1; } }

也有人一邊計算表格，一邊記錄最大值。這種寫法只能求出其中一個最長空白的位置。

void largest_empty_interval() { // [initial states] memset(length, 0, sizeof(length)); // [computation] int max_length = 0; int index = 0; for (int i=1; i<=10; i++) if (array[i] == 1) { length[i] = length[i-1] + 1; if (length[i] > max_length) { max_length = length[i]; index = i; } } // 輸出結果 cout << "最長空白的長度是" << max_length; cout << "有一個最長空白的位置是" << "從" << (index - max_length + 1) - 1 << "到" << (index ) - 1; }

largest empty rectangle

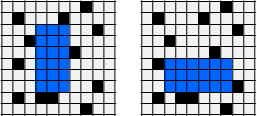
一張方格紙，許多格子填入黑色。請找出不包含黑格子的矩形，令矩形面積盡量大。

UVa 10074 10502 10667

直覺的演算法：窮舉法

矩形的頂點，以下是指一個格子，而不是直線與橫線的交叉點。

矩形總共四個頂點，窮舉所有可能的頂點位置。紙的長寬為H和W，總共HW個位置可以放上頂點。窮舉所有矩形，時間複雜度O((HW)⁴)。另外還得確認矩形不含黑格子，成為O((HW)⁵)。

想要確定一個矩形的大小和位置，其實只要兩個對角頂點就夠了；窮舉所有矩形，時間複雜度O((HW)²)。確認矩形不含黑格子，成為O((HW)³)。

想要確定一個矩形的大小和位置，也可以利用左上角的頂點、長、寬；窮舉所有矩形，時間複雜度O((HW)²)。確認矩形不含黑格子，成為O((HW)³)。

預先計算二維累積和，就能迅速計算二維區間和，時間複雜度O(HW)。窮舉所有矩形，同時確認矩形不含黑格子：判斷矩形面積與區間和是否相等，成為O((HW)²)。

簡單的演算法

接著試試dynamic programming吧！

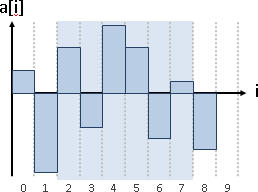
原來的紙張又大又複雜，計算面積非常麻煩。我們試著將紙張切成小塊，逐一處理。這裡將紙張切成橫條。

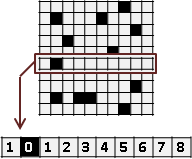
窮舉紙張上的每個位置（窮舉矩形右下角頂點），觀察以上每個橫條（窮舉矩形高度），往左可延伸的長度（預先用largest empty interval得到矩形寬度），持續記錄最大矩形面積。

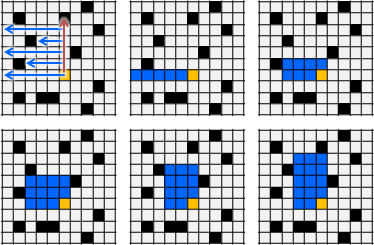
時間複雜度分析：一、每個橫條計算largest empty interval。二、窮舉矩形右下角頂點，窮舉矩形高度，計算矩形面積。時間複雜度O((HW)⋅H)。

空間複雜度分析：儲存全部問題的答案，空間複雜度O(HW)。只想計算一個特定問題的答案，空間複雜度仍是O(HW)。

可以改為切直條。可以改為窮舉矩形右上角頂點。道理都一樣。

程式碼

為了不超出邊界、導致溢位，於是在紙張外面多圍一圈。這是實作二維地圖的常見手法。

bool array[10+2][10+2]; // 空敞處為true，有障礙物則為false

然後是一個橫條的largest empty interval。

int width[10+2]; // 一個橫條上，每個位置往左可延伸的長度 // 如width[2]就是第二個位置往左可延伸的長度 // 初始化為零 void only_one_bar() { // 計算每個點往左可延伸的長度 for (int j=1; j<=10; ++j) if (position j have blockade) // 有障礙物，長度為0。 width[j] = 0; else // 沒障礙物，長度增加。 width[j] = width[j-1] + 1; }

補足程式碼，計算所有橫條。

bool array[10+2][10+2]; int width[10+2][10+2]; void all_bars() { for (int i=1; i<=10; ++i) // 計算每個橫條 for (int j=1; j<=10; ++j) if (array[i][j]) width[i][j] = width[i][j-1] + 1; else width[i][j] = 0; }

計算largest empty rectangle。

bool array[10+2][10+2]; int width[10+2][10+2]; int largest_empty_rectangle() { /* 計算所有橫條當中，每個位置往左可延伸的長度。 */ for (int i=1; i<=10; ++i) for (int j=1; j<=10; ++j) if (array[i][j]) width[i][j] = width[i][j-1] + 1; else width[i][j] = 0; /* 計算每個位置當作矩形右下角頂點時的最大矩形面積。 */ // 最大矩形面積，初始化為最小值 int area = 0; // 窮舉矩形右下角頂點的位置 for (int i=1; i<=10; ++i) for (int j=1; j<=10; ++j) { int w = 1e9; for (int h=1; i-h+1 >= 0; ++h) { if (width[i-h+1][j] == 0) break; w = min(w, width[i-h+1][j]); area = max(area, w*h); } } return area; }

更好的演算法

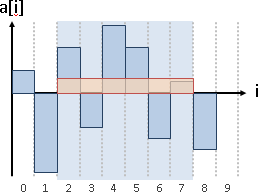
窮舉紙張每一個位置（下邊界），先往上延伸到底（上邊界），再往左右延伸到底（左右邊界），計算面積。

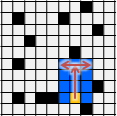
紙張依舊切成橫條。建立由上到下（上邊界）、由左到右（左邊界）、由右到左（右邊界），一共三種largest empty interval，以此為基礎來計算面積。

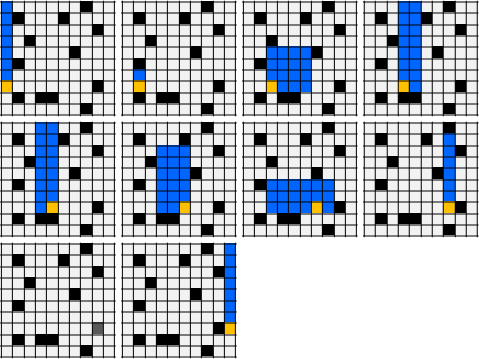
時間複雜度O(HW)。

bool array[10+2][10+2]; int wl[10+2]; // 每一條橫條往左可延伸的長度 int wr[10+2]; // 每一條橫條往右可延伸的長度 int h[10+2]; // 矩形往上可延伸的高度 int l[10+2]; // 矩形往上延伸到底後，往左可延伸的距離。 int r[10+2]; // 矩形往上延伸到底後，往右可延伸的距離。 int largest_empty_rectangle() { // 最大矩形面積，初始化為最小值 int max_area = 0; // 以每一個橫條當作長方形底部 for (int i=1; i<=10; ++i) { // 往左可延伸的長度 for (int j=1; j<=10; ++j) if (array[i][j]) wl[j] = wl[j-1] + 1; else wl[j] = 0; // 往右可延伸的長度 for (int j=10; j>=1; --j) if (array[i][j]) wr[j] = wr[j+1] + 1; else wr[j] = 0; // 矩形往上可延伸的高度 for (int j=1; j<=10; ++j) if (array[i][j]) h[j] = h[j] + 1; else h[j] = 0; // 矩形往上延伸到底，往左可延伸的距離。 for (int j=1; j<=10; ++j) if (l[j] == 0) l[j] = wl[j]; else l[j] = min(wl[j], l[j]); // 矩形往上延伸到底後，往右可延伸的距離。 for (int j=1; j<=10; ++j) if (r[j] == 0) r[j] = wr[j]; else r[j] = min(wr[j], r[j]); // 記錄 largest empty rectangle for (int j=1; j<=10; ++j) max_area = max(max_area, (l[j] + r[j] - 1) * h[j]); } return max_area; }

最好的演算法

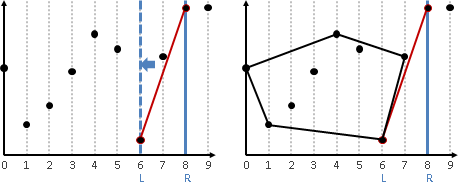
利用一個stack，宛如判斷括號對稱，找出矩形的左右邊界。

時間複雜度O(HW)。

0-1.
以此為例。

   0000000000000000
   0000011111000001
   0011111111100001
   0111111111110001
   1111111111110011
   1111111111111111
   0000000000000000

0-2.
計算每個直條的largest empty interval。

   0000000000000000
   0000011111000001
   0011122222100002
   0122233333210003
   1233344444320014
   2344455555431125
   0000000000000000

0-3.
引入堆疊。堆疊「從下到上」必須是遞增的。
為了方便起見，從倒數第二個橫條開始執行。

   0000000000000000                  
   0000011111000001   |             |
   0011122222100002   |             |
   0122233333210003   |             |
   1233344444320014   |             |
-> 2344455555431125   |             |
   0000000000000000   +-------------+

1.
首先遇到「高度2」。「高度2」塞入堆疊。

   0000000000000000                  
   0000011111000001   |             |
   0011122222100002   |             |
   0122233333210003   |             |
   ^233344444320014   |             |
   ^344455555431125   | 高度2 位置1 |
   0000000000000000   +-------------+
                   
2.
遇到「高度3」。「高度3」>「高度2」，「高度3」塞入堆疊。

   0000000000000000                  
   0000011111000001   |             |
   0011122222100002   |             |
   0^22233333210003   |             |
   1^33344444320014   | 高度3 位置2 |
   2^44455555431125   | 高度2 位置1 |
   0000000000000000   +-------------+

3.
   0000000000000000                  
   0000011111000001   |             |
   00^1122222100002   |             |
   01^2233333210003   | 高度4 位置3 |
   12^3344444320014   | 高度3 位置2 |
   23^4455555431125   | 高度2 位置1 |
   0000000000000000   +-------------+

4.
   0000000000000000                  
   0000011111000001   |             |
   001^122222100002   |             |
   012^233333210003   | 高度4 位置3 |
   123^344444320014   | 高度3 位置2 |
   234^455555431125   | 高度2 位置1 |
   0000000000000000   +-------------+

5.
   0000000000000000                  
   0000011111000001   |             |
   0011^22222100002   |             |
   0122^33333210003   | 高度4 位置3 |
   1233^44444320014   | 高度3 位置2 |
   2344^55555431125   | 高度2 位置1 |
   0000000000000000   +-------------+

6.
   0000000000000000                  
   00000^1111000001   |             |
   00111^2222100002   | 高度5 位置6 |
   01222^3333210003   | 高度4 位置3 |
   12333^4444320014   | 高度3 位置2 |
   23444^5555431125   | 高度2 位置1 |
   0000000000000000   +-------------+

7.
   0000000000000000                  
   000001^111000001   |             |
   001112^222100002   | 高度5 位置6 |
   012223^333210003   | 高度4 位置3 |
   123334^444320014   | 高度3 位置2 |
   234445^555431125   | 高度2 位置1 |
   0000000000000000   +-------------+

8.
   0000000000000000                  
   0000011^11000001   |             |
   0011122^22100002   | 高度5 位置6 |
   0122233^33210003   | 高度4 位置3 |
   1233344^44320014   | 高度3 位置2 |
   2344455^55431125   | 高度2 位置1 |
   0000000000000000   +-------------+

9.
   0000000000000000                  
   00000111^1000001   |             |
   00111222^2100002   | 高度5 位置6 |
   01222333^3210003   | 高度4 位置3 |
   12333444^4320014   | 高度3 位置2 |
   23444555^5431125   | 高度2 位置1 |
   0000000000000000   +-------------+

10.
   0000000000000000                  
   000001111^000001   |             |
   001112222^100002   | 高度5 位置6 |
   012223333^210003   | 高度4 位置3 |
   123334444^320014   | 高度3 位置2 |
   234445555^431125   | 高度2 位置1 |
   0000000000000000   +-------------+

11.
遇到「高度4」。比堆疊頂端的「高度5」還小。
換句話說，高度5的矩形，已經到了盡頭、到了右邊界。
彈出「高度5」，計算面積吧！
面積 = 高度5 × (位置11 - 位置6) = 25

   0000000000000000     高度5 位置6  
   00000#####000001   |             |
   00111#####^00002   |             |
   01222#####^10003   | 高度4 位置3 |
   12333#####^20014   | 高度3 位置2 |
   23444#####^31125   | 高度2 位置1 |
   0000000000000000   +-------------+

12.
遇到「高度3」。比堆疊頂端還小！彈出！
面積 = 高度4 × (位置12 - 位置3) = 36

   0000000000000000     高度4 位置3  
   0000011111000001   |             |
   00#########00002   |             |
   01#########^0003   |             |
   12#########^0014   | 高度3 位置2 |
   23#########^1125   | 高度2 位置1 |
   0000000000000000   +-------------+

13-1.
面積 = 高度3 × (位置13 - 位置2) = 33

   0000000000000000     高度3 位置2  
   0000011111000001   |             |
   0011122222100002   |             |
   0###########0003   |             |
   1###########0014   |             |
   2###########^125   | 高度2 位置1 |
   0000000000000000   +-------------+

13-2.
面積 = 高度2 × (位置13 - 位置1) = 24

   0000000000000000     高度2 位置1  
   0000011111000001   |             |
   0011122222100002   |             |
   0122233333210003   |             |
   ############0014   |             |
   ############^125   |             |
   0000000000000000   +-------------+

13-3.
「高度1」塞入堆疊。可以想成：「高度1」比目前堆疊頂端還大。
注意到，「位置1」沿用上一個彈出的位置。

   0000000000000000                  
   0000011111000001   |             |
   0011122222100002   |             |
   0122233333210003   |             |
   1233344444320014   |             |
   234445555543^125   | 高度1 位置1 |
   0000000000000000   +-------------+

14.
   0000000000000000                  
   0000011111000001   |             |
   0011122222100002   |             |
   0122233333210003   |             |
   1233344444320014   |             |
   2344455555431^25   | 高度1 位置1 |
   0000000000000000   +-------------+

15.
   0000000000000000                  
   0000011111000001   |             |
   0011122222100002   |             |
   0122233333210003   |             |
   12333444443200^4   | 高度2 位置15|
   23444555554311^5   | 高度1 位置1 |
   0000000000000000   +-------------+

16.
   0000000000000000                  
   000001111100000^   |             |
   001112222210000^   |             |
   012223333321000^   | 高度5 位置16|
   123334444432001^   | 高度2 位置15|
   234445555543112^   | 高度1 位置1 |
   0000000000000000   +-------------+

17-1.
最後記得處理堆疊剩下的元素。
面積 = 高度5 × (位置17 - 位置16) = 5

   0000000000000000     高度5 位置16 
   000001111100000#   |             |
   001112222210000#   |             |
   012223333321000#   |             |
   123334444432001#   | 高度2 位置15|
   134445555543112#   | 高度1 位置1 |
   0000000000000000   +-------------+

17-2.
面積 = 高度2 × (位置17 - 位置15) = 4

   0000000000000000     高度2 位置15 
   0000011111000001   |             |
   0011122222100002   |             |
   0122233333210003   |             |
   12333444443200##   |             |
   13444555554311##   | 高度1 位置1 |
   0000000000000000   +-------------+

17-3.
面積 = 高度1 × (位置17 - 位置1) = 16

   0000000000000000     高度1 位置1  
   0000011111000001   |             |
   0011122222100002   |             |
   0122233333210003   |             |
   1233344444320014   |             |
   ################   |             |
   0000000000000000   +-------------+

largest empty square

area(i, j)
= min( area(i-1, j), area(i-1, j-1), area(i, j-1) ) + 1

窮舉紙張上的每個位置，作為正方形右下角，計算正方形面積：看看正方形的右上角、左上角、左下角最遠到哪裡。

時間複雜度O(HW)，空間複雜度O(min(H, W))。

bool array[10+1][10+1]; // 空敞處為true，有障礙物則為false。 int area[10+1][10+1]; // 初始化為零 int largest_empty_square() { int a = 0; for (int i=1; i<=10; ++i) for (int j=1; j<=10; ++j) { if (array[i][j]) area[i][j] = min( area[i-1][j], area[i][j-1], area[i-1][j-1] ) + 1; if (area[i][j] > a) // 記錄最大值 a = area[i][j]; } return a; }

UVa 10908

maximum sum subarray

2 -7  4 -3  6  4 -4  1 -5 0
      \______  ______/
             \/
             8

總和最大的區間。從數列當中取出一連串數字，求總和；找出最大的總和。最糟糕的情況，就是不取任何數字，總和為零。

可能不只一種。

窮舉法。窮舉區間起點、區間終點，計算總和。時間複雜度O(N³)。

貪心法。累計總和，遇到負數就捨棄。時間複雜度O(N)。

int a[10] = {1, 2, -6, 3, -2, 4, -1, 3, 2, -4}; // 計算maximum sum subarray之元素總和（可以不必取數字） int maximum_sum_subarray() { int max_sum = 0, sum = 0; for (int i=0; i<10; ++i) { sum += a[i]; // 累計總和 if (sum < 0) sum = 0; // 零總比負數好 // 隨時記錄最大值 if (sum > max_sum) max_sum = sum; } return max_sum; } int a[10] = {1, 2, -6, 3, -2, 4, -1, 3, 2, -4}; // 計算maximum sum subarray之元素總和（至少取一個數字） int maximum_sum_subarray() { int max_sum = -1e9, sum = 0; for (int i=0; i<10; ++i) { // 先前累積的不是負數，加了就更大。 if (sum > 0) sum += a[i]; // 先前累積的若是負數，寧可不加。 else sum = a[i]; // 隨時記錄最大值 if (sum > max_sum) max_sum = sum; } return max_sum; } int a[10] = {1, 2, -6, 3, -2, 4, -1, 3, 2, -4}; // 找出其中一個maximum sum subarray的位置（最左邊的） int maximum_sum_subarray() { int max_sum = 0, sum = 0; int start = 0, end = 0, temp_start = 0; for (int i=0; i<10; ++i) { sum += a[i]; if (sum < 0) { sum = 0; temp_start = i+1; // 重新設定起點是下一個數字 } if (sum > max_sum) { max_sum = sum; start = temp_start; end = i; } } if (start > end) cout << "什麼數字都不取"; else cout << "從" << start << "到" << end; return max_sum; }

UVa 507 10684

maximum sum submatrix

這個問題還可推廣到2D、3D，時間複雜度分別是O(N³)、O(N⁵)。原理是面與面合併，條與條合併，元素與元素合併。以下直接提供3D的情形。

const int A = 20, B = 20, C = 20; // 三個維度的個別寬度 int max1D(int a[]) { int ans = -1e9; int s = 0; for (int i=0; i<C; ++i) { if (s >= 0) s += a[i]; else s = a[i]; ans = max(ans, s); } return ans; } int max2D(int a[][20]) { int ans = -1e9; int s[20]; for (int i=0; i<B; ++i) { memset(s, 0, sizeof(s)); for (int j=i; j<B; ++j) { for (int k=0; k<C; ++k) s[k] += a[j][k]; ans = max(ans, max1D(s)); } } return ans; } int max3D(int a[][20][20]) { int ans = -1e9; int s[20][20]; for (int i=0; i<A; ++i) { memset(s, 0, sizeof(s)); for (int j=i; j<A; ++j) { for (int k=0; k<B; ++k) for (int l=0; l<C; ++l) s[k][l] += a[j][k][l]; ans = max(ans, max2D(s)); } } return ans; } int main() { int a[20][20][20]; cout << max3D(a); return 0; }

UVa 108 836 10827 10755

maximum sum submatrix in sparse matrix

當矩陣幾乎都是零，數字很少，時間複雜度O(N+K²)。N是矩陣橫向寬度，K是數字個數。

限制子矩陣的上下邊界位置，並且預先計算直向累積和，此時問題退化為一維maximum sum subarray。

窮舉子矩陣上邊界。針對一種上邊界，依序窮舉下邊界，橫條漸漸增加。針對一種下邊界，更新直向累積和，計算橫向maximum sum subarray。

const int N = 100; // 橫向寬度 int s[N]; // 直向累積和 const int K = 10; // 數字個數 struct Element {int i, j, n;} a[K]; // 數字位置與數字大小 bool operator<(Element a, Element b) { return a.i < b.i || (a.i == b.i && a.j < b.j); } int maximum_sum_submatrix() { sort(a, a+K); vector<int> row; for (int i=0; i<K; ++i) if (i == 0 || a[i].i != a[i-1].i) row.push_back(i); row.push_back(K); int ans = 0; for (int i=0; i<(int)row.size(); ++i) { for (int j=0; j<N; ++j) s[j] = 0; for (int j=i; j<(int)row.size(); ++j) { for (int k=row[j]; k<row[j+1]; ++k) s[a[k].j] += a[k].n; ans = max(ans, maximum_sum_subarray(s, N)); } } return ans; } const int N = 100; // 橫向寬度 int s[N]; // 直向累積和 const int K = 10; // 數字個數 struct Element {int i, j, n;} a[K]; // 數字位置與數字大小 bool operator<(Element a, Element b) { return a.i < b.i || (a.i == b.i && a.j < b.j); } int maximum_sum_submatrix() { sort(a, a+K); int ans = 0; for (int i=0; i<K; ++i) { while (i > 0 && a[i].i == a[i-1].i) i++; for (int j=0; j<N; ++j) s[j] = 0; for (int j=i; j<K; ++j) { while (j > 0 && a[j].i == a[j-1].i) { s[a[j].j] += a[j].n; j++; } ans = max(ans, maximum_sum_subarray(s, N)); } } return ans; }

maximum sum subarray of length K

窮舉所有可能的區間位置。時間複雜度O(N)。

網路上有人暱稱此技巧為「滑動視窗sliding window」。

int a[10] = {1, 2, -6, 3, -2, 4, -1, 3, 2, -4}; int maximum_sum_subarray(int K) { int sum = 0; for (int i=0; i<K; ++i) sum += a[i]; int ans = sum; for (int i=0, j=K; j<10; ++i, ++j) { // sum += a[j]; sum -= a[i]; sum += a[j] - a[i]; if (sum > ans) ans = sum; } return ans; }

ICPC 2678 4840

maximum sum subarray of length [L, R]

窮舉法。窮舉區間起點、區間終點，求總和。時間複雜度O(N³)。

欲讓a[i...j]最大，即是讓累積和a[0...i-1]最小。窮舉所有位置作為區間右端，至於區間左端則套用「滑動視窗最小值」的模型：

以binary search tree動態儲存[L,R]範圍內的所有累積和。時間複雜度O(NlogN)。

以deque動態儲存[L,R]範圍內的累積和，保持嚴格遞增。時間複雜度O(N)。

maximum average subarray（maximum density segment）

區間總和除以區間長度，平均數最大的區間。

直接法。當數列沒有正數，則區間長度是0。當數列有正數，區間長度越小，平均數越大；區間長度是1，平均數最大，位於數列最大值。時間複雜度O(N)。

計算幾何。計算累積和sum[i]，可快速求得區間[i, j]的平均數(sum[i] - sum[j-1]) / (i - (j-1))。進一步想成：數對(i, sum[i])與數對(j-1, sum[j-1])相減後算y/x！

原問題變成：點集合(i, sum[i])與點集合(-i, -sum[i])的pairwise sum當中，求y/x最大者。一定位於凸包的頂點。

凸包有著很快的演算法。將pairwise sum拓展成Minkowski sum，改以多邊形的觀點來看問題。兩個多邊形的Minkowski sum的凸包，就是兩個多邊形的凸包的Minkowski sum。得到簡潔的演算法：求(i, sum[i])的凸包，求(-i, -sum[i])的凸包，求Minkowski sum，找到y/x最大的頂點。時間複雜度O(N)。

maximum average subarray of length K

滑動視窗，O(N)。

maximum average subarray of length [L, R]

不能是空區間。總和為正數，區間越短越有利；總和為負數，區間越長越有利。

窮舉法。窮舉區間起點、區間終點，求平均。時間複雜度O(N³)。

試誤法。窮舉區間長度，求符合長度的maximum average subarray，滑動視窗。時間複雜度O(N²)。

試誤法。二元搜尋平均數，總共logR個回合。針對一種平均數，所有數字皆減去平均數，求maximum sum subarray。若是空區間，則平均數須更大；若非空區間，則平均數可更小。時間複雜度O(NlogR)。

計算幾何。建構二維座標系，索引值為X軸，累積和為Y軸，(i, sum[i])為N個點座標，區間即線段，區間平均數即線段斜率，平均數最大的區間即斜率最大的線段。

套用「sweep line」，先窮舉區間右邊界，再窮舉區間左邊界。斜率最大的線段，就是右端點到左方所有點的下切線！換句話說，就是右端點到左方所有點的凸包的下切線！

改為套用「Andrew's monotone chain」，只求下凸包。建立stack，逐次加入一點，找到下切線，更新凸包。所有下切線當中，斜率最大者，即為答案。時間複雜度O(N)。

區間擁有寬度限制時，只求該範圍的下凸包。

寬度下限：額外的新下切線作為答案。

寬度上限：困難處在於刪除下凸包的最左側頂點，並且快速地重新包覆。解決方法是預計算：上述演算法事先從右到左掃描，求得下凸包的演變過程，反過來運作，就是刪除了。

int N, L; // R is N... int a[100+1]; int sum[100+1]; int deque[100+1], *qf, *qb; int cmp(int x1, int x2, int x3, int x4) { return (sum[x2] - sum[x1 - 1]) * (x4 - x3 + 1) - (sum[x4] - sum[x3 - 1]) * (x2 - x1 + 1); } void maximum_average_subarray() { for (int i = 1; i <= N; ++i) sum[i] = sum[i-1] + a[i]; int ansL = 1, ansR = L; qf = qb = deque; for (int i = L; i <= N; ++i) { while (qb-qf >= 2 && cmp(qb[-2], i-L, qb[-1], i-L) >= 0) qb--; *qb++ = i-L+1; while (qb-qf >= 2 && cmp(qf[0], i, qf[1], i) <= 0) qf++; int c = cmp(qf[0], i, ansL, ansR); if (c > 0 || c == 0 && i - qf[0] < ansR - ansL) ansL = qf[0], ansR = i; } cout << ansL << ' ' << ansR << '\n'; }

ICPC 4726 3716

k maximum sum subarray

k個不重疊區間，數字總和盡量大。

此技巧尚無正式名稱，英文網路稱作「Lagrangian Relaxation」或「Aliens Trick」。

https://www.ptt.cc/bbs/Prob_Solve/M.1613627212.A.145.html
http://www.serbanology.com/article/The%20Trick%20From%20Aliens
https://mamnoonsiam.github.io/posts/attack-on-aliens.html
https://soi.ch/wiki/alien-optimization/
https://robert1003.github.io/2020/02/26/dp-opt-wqs-binary-search.html
https://tioj.ck.tp.edu.tw/uploads/attachment/5/51/10.pdf
https://hackmd.io/@wiwiho/CPN-aliens