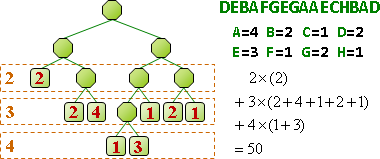
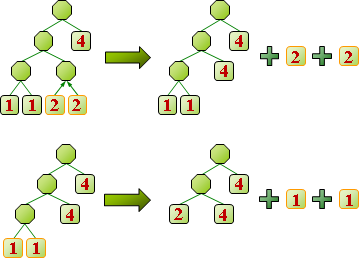
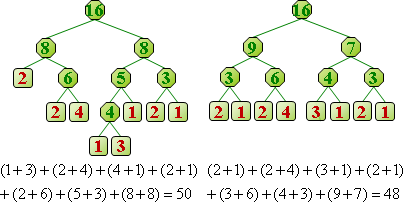
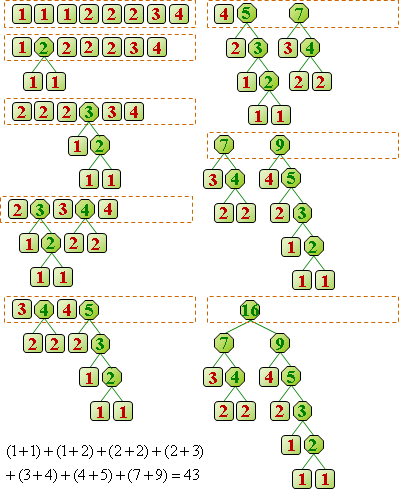
compression
濃縮資料

如何簡明扼要的記載資料、傳述訊息呢?

縮短資料長度,減少交流時間,減少儲存空間,好處多多。
壓縮方式
二元碼壓縮:二元碼縮短成另一個二元碼。本文主角。
compress
001100111100101010100001 -------------> 10110101
<-------------
decompress
文字壓縮:例如doctor縮寫成Dr.、公共汽車簡稱為公車。
vs. versus lol laugh out loudly RTFM read the fucking manual afaik as far as I known ¥ Japanese Yen
語言壓縮:長話短說。文學的範疇。
原文 |壓縮 |失真壓縮|言簡意賅 如果你沒勇氣陪我到|若你畏懼陪我到|不愛我 |再見 明天的明天的明天 |大後天 | | 倒不如就忘了就斷了|不如忘盡 |就忘了我| 寂寞的昨天的昨天 |寂寞的前天 | |
資訊壓縮:古代人將壓縮和編碼視為相同。抽象的資訊信息變成具體的文字符號,以三言兩語詮釋大千世界。
打個比方,白話文是不太理想的壓縮、文言文是更理想的壓縮;北京話是不太理想的壓縮、山東話是更理想的壓縮。
北京話 |台灣話 |閩南話 |四川話 |山東話 甲:是誰在樓下啊?|甲:誰在下面?|甲:啥咪郎?|甲:喇國?|甲:誰? 乙:是我在這兒唄!|乙:我在這裡!|乙:喜哇啦!|乙:使握!|乙:俺! 甲:你在做什麼咧?|甲:你在幹嘛?|甲:衝啥悔?|甲:昨傻?|甲:啥? 乙:我在這小便吶!|乙:我在小便!|乙:棒溜啦!|乙:潦瞭!|乙:尿!
compress / decompress
「壓縮」是濃縮資料,「解壓縮」是回復資料。觀念類似先前提及的「編碼」與「解碼」。
compress
thank you! -------------> 3Q!
<-------------
decompress
compress
200000000美金 -------------> 兩億鎂
<-------------
decompress
資料先壓縮、再解壓縮,如果還是跟原本資料一模一樣,就叫做「無失真壓縮lossless compression」;如果不一樣就叫做「失真壓縮lossy compression」。
用電腦處理資料,首重精準無誤。以下僅介紹無失真壓縮。
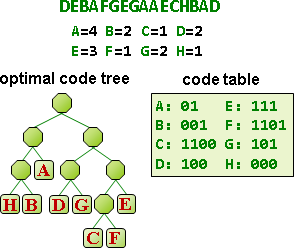
symbol / code
資料通常很長。大家習慣逐段處理,符合電腦運作特性。
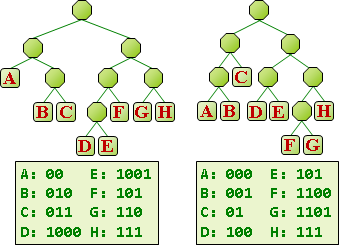
一段資料構成一個「符號」,再進一步變成簡短的「碼」。常見段落設定成符號,相同的符號對應相同的碼,有利於辨認。

制定符號:尚無最佳演算法,仍有研究空間。經典演算法是Lempel–Ziv compression。
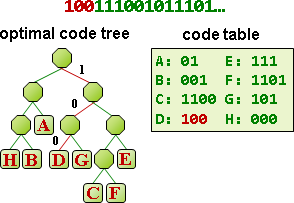
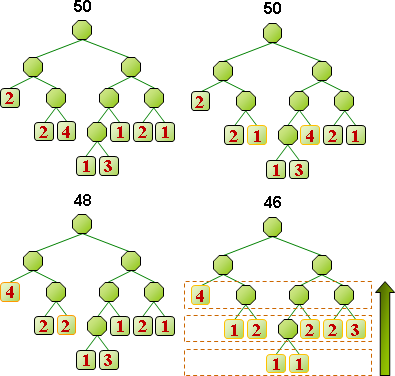
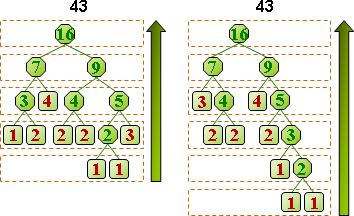
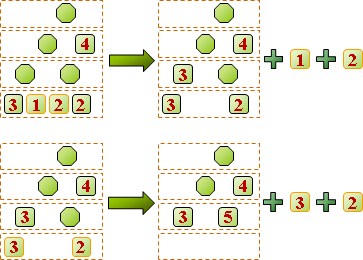
制定碼:已有最佳演算法,讓碼的總長度達到最小值!經典演算法是arithmetic compression、Huffman compression。
兩者相互配合,產生了各式各樣的演算法:DEFLATE、gzip、bzip2、zopfli、brotli。有興趣的讀者請自行學習。
編碼與壓縮的差別。編碼:公定符碼表格,符號長度是一個字元,碼長度是整數個byte。壓縮:自訂符碼表格,長度不定。
【註:因為逐段處理,所以沒有活用文字先後順序。】
何謂好的壓縮?
預先計算符碼,才能順利壓縮。符碼表格與壓縮結果一併儲存,才能順利解壓縮。
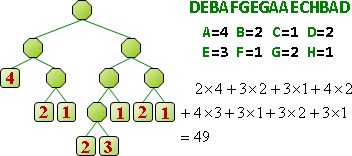
所謂好的壓縮,就是讓「壓縮後長度」加「符碼表格長度」少於「壓縮前長度」。
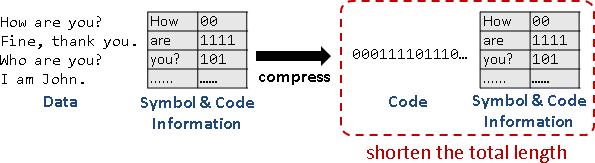
順帶一提,由於必須額外儲存符碼表格,檔案可能越壓越大!比方說,已經壓縮過的資料再壓縮一遍,很容易產生這種情形。