closest pair
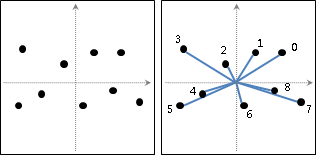
一群點當中,距離最近的兩個點叫作「最近點對」。
演算法(enumeration)
窮舉法,時間複雜度O(N²),可以找出所有的最近點對。
實作時,減少sqrt函式的呼叫次數,盡量記錄距離的平方,可以減少計算時間。
演算法(sweep line)
預先按照水平座標排序,再以水平距離裁減搜尋範圍。
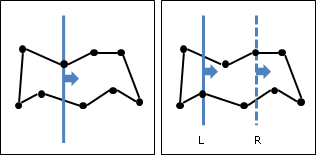
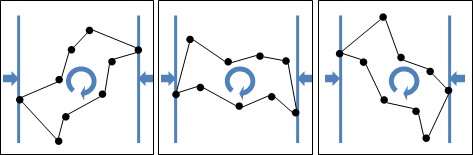
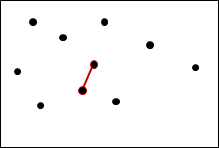
一、先排序所有點,以X座標為主,Y座標無所謂。
二、從左往右掃,依序窮舉各點作為左端點。
甲、從左端點開始往右掃,依序窮舉各點作為右端點。
乙、若左右兩點距離差太遠、超過目前發現的最近點對距離,
就可以停止窮舉右端點。
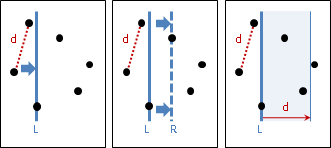
也可以先窮舉右端點、再窮舉左端點。下個段落會用到。
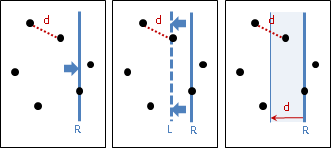
最差情況是所有點都在同一條垂直線上,將會窮舉到所有點對,完全無法裁減搜尋範圍。儘管時間複雜度仍是O(N²),但是實際效率極佳。我不清楚平均時間複雜度是多少。
實作時,避免直接排序原資料,複製一份指標或索引值來排序,可以減少計算時間。
UVa 10245 10750 11378 ICPC 6666
演算法(sweep line)
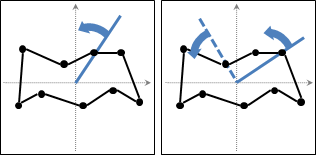
要避免最差情況,有個想法是:再將所有點依照垂直方向排序。如此一來,時間複雜度降低為O(NlogN)。
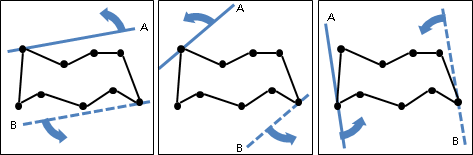
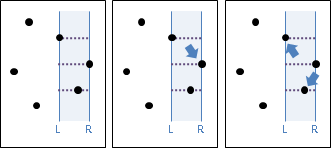
一、位於右端點左方、距離d以下的點,才有可能形成最近點對。也就是以右端點為圓心、左半圓涵蓋的點(包含邊界)。照理來說,我們只需要檢查半圓範圍裡面的點。
運用左掃描線作為輔助,跟隨右掃描線亦步亦趨,我們得以輕易的過濾出水平距離d以下的點,但是無法進一步過濾出半徑距離d以下的點。
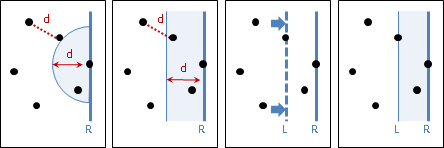
折衷的方式是依照Y座標排序水平距離d以下的點,然後運用二元搜尋法找到右端點,然後找到Y座標比右端點稍大、稍小的點──這些點很可能就在半圓之內。
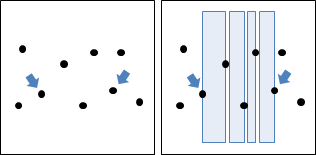
二、右端點左方的點,兩兩之間的距離,至少是d。
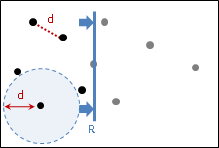
點與點之間無法太過密集擁擠,能夠組成最近點對的左端點並不多。其實只需檢查右端點的前兩點、後兩點,作為左端點,就能囊括所有最近點對!
最極端的情況,是以右端點為中心、左半正方形涵蓋的點(包含邊界)。
由於右掃描線不斷往右移動,水平距離d以下的點必須不斷重新排序,很花時間。運用binary tree資料結構,即可隨時保持排序,節省時間。
一、預先排序所有點,X座標為主,Y座標為輔。
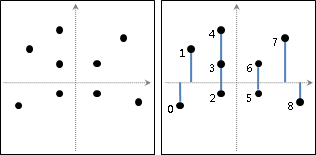
二、建立一棵平衡二元樹(AVL tree),
儲存右端點的左方、水平距離小於等於d的點。
二元樹排序以Y座標為主,X座標為輔。一開始是空的。
d是當下的最近點對距離。一開始是無限大。
三、右掃描線依序窮舉各點作為右端點。
甲、二元樹刪除與右端點水平距離大於d的點們。
(左掃描線視情況往右移動。)
乙、二元樹加入右端點。
丙、二元樹尋找右端點的前兩點與後兩點,嘗試更新最近點對。
掃描線輔以資料結構,是計算幾何的經典手法,請讀者牢記在心。
時間複雜度。排序O(NlogN)。掃描線O(N)。二元樹總共刪除N個點、加入N個點、尋找5N個點,O(NlogN)。
【待補程式碼】
演算法(divide-and-conquer method)
時間複雜度O(NlogN),可以找出所有的最近點對。原理是把平面切割成左右兩側,答案分為「最近點對在左側」、「最近點對在右側」、「最近點對橫跨兩側」三種情形。先將左側與右側分別遞迴求解之後,再利用左側與右側的答案,快速算出橫跨兩側的答案。
preprocessing:
一、排序所有點,以X座標為主,Y座標無所謂。O(NlogN)
二、檢查是否有共點。如果有,就找出所有共點,演算法結束。O(N)
divide:
把所有點分為左右兩側,左側、右側的點數盡量一樣多。
conquer:
左側、右側分別遞迴求解。
combine:
一、利用左側、右側的最佳解d,求出橫跨兩側的解:
甲、首先找出靠近中線的點,水平距離小於d、包含d。O(N)
(小於d、不包含d,則只找出其中一組最近點對。)
乙、排序這些點,Y座標為主,X座標為輔。O(NlogN)
丙、每一個點都找其上方鄰近的點,看看能不能形成最近點對。
只需檢查至後三點。O(N⋅3) = O(N)
二、答案為左側、右側、橫跨兩側,三者當中的最佳解。
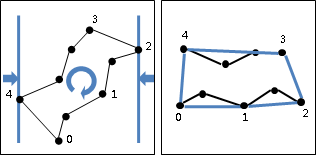
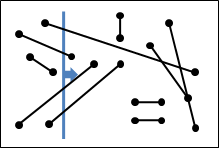
以下提供釋例。畫面上有一些點。
把點分為左側與右側,點數盡量一樣多。左側與右側的交界處可能會銜接,也可能不會銜接。左右兩側通常是不一樣寬的。
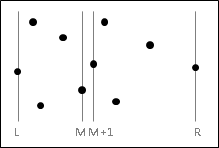
左側、右側分別遞迴求解,最後求得這兩種情況下的最近點對。最近點對的距離為d。
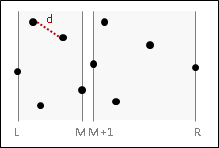
左側的每一個點,半徑d以內的範圍(不包含邊界),不會有其他左側的點存在,只可能出現另一側的點。右側亦然。
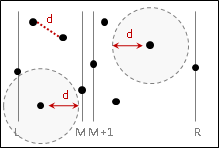
要找出橫跨兩側的點對,可以從左側的右邊線,往左距離d以內的範圍裡(包含邊界)的這些點,有可能與右側的點形成最近點對。
也可以以右側的左邊線為主。
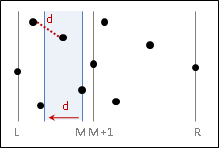
從左側的右邊線,往右距離d以內的範圍裡的這些點,則是可能的另一頭端點的範圍。
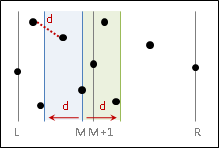
要找出橫跨兩側的最近點對,只要依序窮舉左側右邊界距離d以內、位於左側的點,作為左端點;再找左側右邊界距離d以內、位於右側的點,作為右端點。
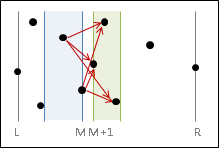
從這裡開始衍生兩種實作方式:
一、最容易理解的方式,是從下往上掃描左端點;針對每個左端點,找到合適的右端點。右側之中,點與點之間的距離至少是d。運用先前的分析手法,我們只需檢查掃描線的中下兩點、上兩點,作為右端點,就能囊括所有橫跨兩側的最近點對。
此處省略分析過程,讀者可以自行畫圖觀察。
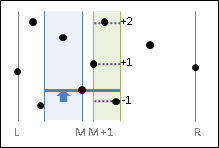
實作時,運用右側掃描線作為輔助,跟隨左側掃描線亦步亦趨,就能快速找到中下兩點、上兩點,而不必使用二元搜尋法。
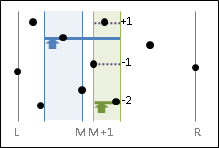
二、另一個難以理解、但是容易實作的方式,是把範圍內的這些點全部混在一起,不分左右,然後從下往上掃描。先窮舉下端點,再尋找上方鄰近的點作為上端點,檢查是否形成最近點對。
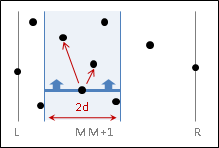
最多只需要檢查下端點的後四點,就一定囊括所有橫跨兩側的最近點對。
此處省略分析過程,讀者可以自行畫圖觀察。蠻複雜的喔!可以先將左側、右側的分布情形分開畫好,再將左右兩側拼在一起。
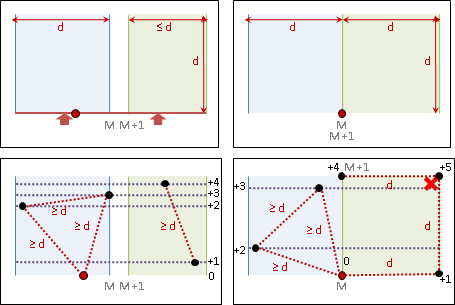
更進一步。第四點一定與同側的另外一點形成最近點對,之後還是能檢查到,所以不必檢查第四點、只需要檢查後三點。
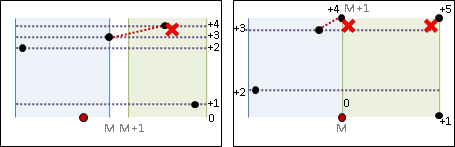
以上圖例都是掃描線掃中左側的點,讀者可以自行分析掃描線掃中右側的點的所有情況。大功告成。
教科書通常只談到後五點;此處深入分析,從後五點逼近至後三點。儘管推理過程讓人感覺很有學問,但是執行時間遠遠高於窮舉法。這種鑽牛角尖又不切實際的學問,不如不學。
時間複雜度O(NlogN + Nlog(N/2) + Nlog(N/4) + ...) = O(NlogN)。