directed acyclic graph（DAG）

沒有環、無向圖，就是先前提到的「樹」、「森林」；沒有環、有向圖，就是現在提到的「有向無環圖」。由於英文名稱很長，所以大家習慣採用縮寫「DAG」，字母皆大寫。

先前我們用延伸拓展的觀點來看待tree；同樣地，我們也可以用延伸拓展的觀點來看待DAG。

DAG沒有環，不走回頭路、永遠不回頭、不斷向前進。DAG可以重新繪製，讓所有邊朝著同一個方向延伸拓展，讓所有點有著先後次序。

在各式各樣的圖之中，tree與DAG是十分重要的特例，往往存在速度極快的演算法。由於tree和DAG沒有環、方向明確，所以我們很容易安排出一個計算順序（一般是採用拓撲順序），循序漸進求得答案，不必受到環的折騰。

source

「源」。只有出邊、沒有入邊的點。概念宛如根。

DAG天生擁有源，不必特地選擇。通常有許多個。

sink

「匯」。只有入邊、沒有出邊的點。概念宛如葉。

DAG天生擁有匯，不必特地選擇。通常有許多個。

現實生活當中的DAG

不斷前進、不會後退，有時分化、有時聚合，就是DAG的最佳寫照。

是DAG：課程擋修規則、族譜、水系、閃電、洗澡。

非DAG：道路交通、食物鏈、人體血脈、山脈、氣流。

以時間軸當作主角，緣起緣滅、緣聚緣散，凡事都是DAG。

UVa 925

楔子

在枚舉所有排列的問題之中，如果我們另外再限制誰要排在誰前方、誰要排在誰後方，那麼在這些限制之下，合理的排列還會剩下哪些呢？

【註：枚舉所有排列，讀者們可另行參考「enumerate permutations」一文。】

先後限制與圖

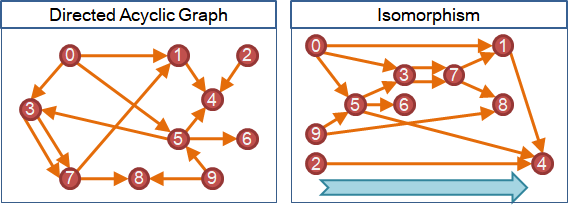
誰要排在誰前方、誰要排在誰後方，其實就是兩兩之間的關係，故可以改用圖來表示：把圖上一條由A點連向B點的邊，想成是A必須排在B前方（B必須排在A後方）。

當然啦，也可以把圖上一條由A點連向B點的邊，想成是A必須排在B後方。不過一般來說我們習慣成自然地使用前者。

topological sort與topological ordering

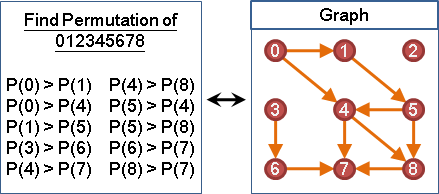
「拓撲排序」是排序一張有向圖的點的方式。把圖上一條由A點連向B點的邊，想成是A必須排在B前方（B必須排在A後方）。「拓撲排序」用來找出合理的排列順序，讓每一個點的先後順序，符合每一條邊所規定的先後順序。

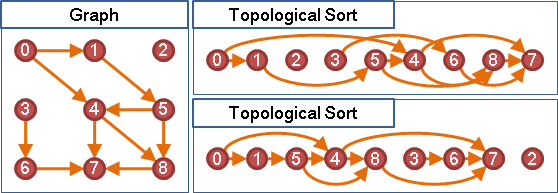
「拓撲順序」是指一張有向圖經過「拓撲排序」後，每一個點的先後順序。一張圖有許多種「拓撲順序」。只要不違背圖上每一條邊的先後規定，要怎麼排列圖上的點都行。

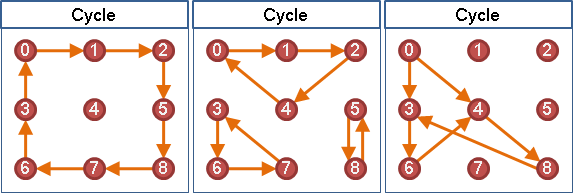
圖上不能有環

當圖上有環，拓樸順序就不存在。因為環上每一個點都會有連向自己的邊，意味著環上每一個點必須排在其他點的後方，環上每一個點都不能在排列順序中拔得頭籌，所以合理的排列順序不存在。

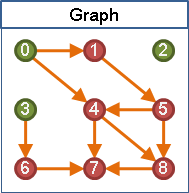
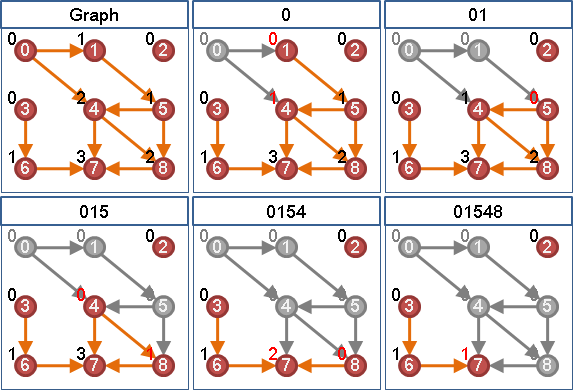
找出一個合理的排列順序（Kahn's algorithm）

要找出合理的排列順序，首先得決定第一點！知道如何找出第一點，那麼就可以循序漸進的再找出第二點、第三點了。

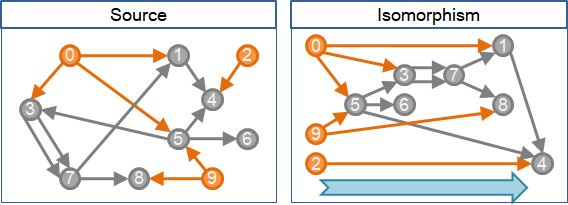
可以作為第一點的點，想必它不必排在其他點後方。也就是說，沒有被任何邊連向的點，就可以作為第一點。如果有很多個第一點，那麼找哪一點都行。

決定第一點之後，那麼剩下所有點都會在第一點後方。所有關於第一點的先後規定，都已經符合了，規定存不存在都無所謂。因此，決定第一點之後，就可以刪去此點，以及刪去由此點連出去的邊──原問題可以遞迴地縮小！

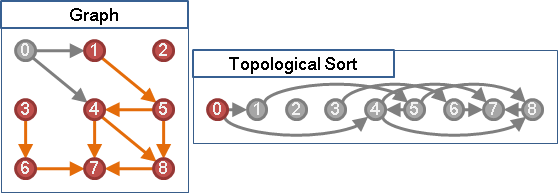
只要反覆尋找沒有被任何邊連向的點，然後刪去此點以及刪去由此點連出去的邊，就可以找出一個合理的排列順序了。

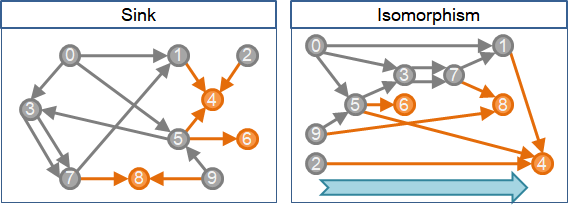
附帶一提，要找出合理的排列順序，也可以由最後一點開始決定！無論要從第一點找到最後一點，或是從最後一點找到第一點，都是可以的。各位可以想想看該怎麼做。

儘管這個問題有遞迴的性質，可以用遞迴語法來實作，但由於遞迴的分支只有一條，故亦可以用迴圈語法。我想大家都會選擇以比較簡單的迴圈語法來實作吧？

實作時，可以利用變數記錄圖上每一個點目前仍被多少條邊連到。尋找沒有被任何邊連向的點，就直接看該變數是不是零；刪去由此點連出去的邊，就順便更新變數的值。

bool adj[9][9]; // adjacency matrix int ref[9]; // 記錄圖上每一個點目前仍被多少條邊連到 void topological_ordering() { for (int i=0; i<9; ++i) ref[i] = 0; // 初始化為0 // 累計圖上每一個點被幾條邊連到 for (int i=0; i<9; ++i) for (int j=0; j<9; ++j) if (adj[i][j]) ref[j]++; // 開始找出一個合理的排列順序 for (int i=0; i<9; ++i) { // 尋找沒有被任何邊連向的點 int s = 0; while (s < 9 && ref[s] != 0) ++s; if (s == 9) break; // 找不到。表示目前殘存的圖是個環。 ref[s] = -1; // 設為已找過（刪去s點） cout << s; // 印出合理的排列順序的第i點 // 更新ref的值（刪去由s點連出去的邊） for (int t=0; t<9; ++t) if (adj[s][t]) ref[t]--; } } vector<int> adj[9]; // adjacency lists int ref[9]; // 記錄圖上每一個點目前仍被多少條邊連到 void topological_ordering() { for (int i=0; i<9; ++i) ref[i] = 0; // 初始化為0 // 累計圖上每一個點被幾條邊連到 for (int i=0; i<9; ++i) for (int j=0; j<adj[i].size(); ++j) ref[adj[i][j]]++; // 宣告一個queue來記錄已經沒有被任何邊連向的點 queue<int> Q; for (int i=0; i<9; ++i) if (ref[i] == 0) Q.push(i); // 開始找出一個合理的排列順序 for (int i=0; i<9; ++i) { // 尋找沒有被任何邊連向的點 if (Q.empty()) break; // 找不到。表示目前殘存的圖是個環。 int s = Q.front(); Q.pop(); ref[s] = -1; // 設為已找過（刪去s點） cout << s; // 印出合理的排列順序的第i點 // 更新ref的值（刪去由s點連出去的邊） for (int j=0; j<adj[s].size(); ++j) { int t = adj[s][j]; ref[t]--; if (!ref[t]) Q.push(t); // 記錄已經沒有被任何邊連向的點 } } }

時間複雜度等於一次graph traversal的時間。圖的資料結構為adjacency matrix是O(V²)；圖的資料結構為adjacency lists是O(V+E)。

這個演算法可以想成是修改過的BFS：沒有被任何邊連向的點才能塞入queue。

UVa 10305 200

找出一個合理的排列順序（depth-first search）

DFS離開點的順序，顛倒之後，正好是拓撲順序。

DFS優先走到最深的點，直到不能再深為止。DFS也會優先找出所有最深的點，離開點的原則是最深的點先離開。最深的點當然就是拓撲順序最後的點。

bool adj[9][9]; // adjacency matrix int visit[9]; // 記錄DFS遍歷過的點 int order[9]; // 儲存一個合理的排列順序 int t; // 時刻 bool cycle; // 記錄DFS的過程中是否偵測到環 void DFS(int i) { // back edge，有環。 if (visit[i] == 1) {cycle = true; return;} // forward edge、cross edge。 if (visit[i] == 2) return; visit[i] = 1; for (int j=0; j<9; ++j) if (adj[i][j]) DFS(j); visit[i] = 2; order[t++] = s; // 記錄合理的排列順序 } void topological_ordering() { // 初始化 for (int i=0; i<9; i++) visit[i] = 0; cycle = false; t = 0; // 進行DFS for (int i=0; i<9; ++i) if (!visit[i]) DFS(i); // 輸出結果 if (cycle) cout << "圖上有環"; else // 印出一個合理的排列順序 // 離開點的順序，頭尾顛倒之後，就是拓撲順序。 for (int i=9-1; i>=0; --i) cout << order[i]; }

找出所有合理的排列順序

請用backtracking。此處不詳述了，直接看練習題吧。

UVa 124

計算所有合理的排列順序個數

請用dynamic programming，時間複雜度O(2ⱽ V²)。

小遊戲：http://www.kongregate.com/games/agame/romance-maker。

延伸閱讀：inhomogeneous sorting

1 2 3 ... N，一共N個數字，由小到大排列。現在制定了一些兩兩相鄰交換的規則，例如規則「18 ↔ 81」就表示1和8相鄰時可以對調。

請問：一、字典順序最大的排列？二、總共幾種不同排列？

不能兩兩相鄰交換，也就是有先後限制。可以兩兩相鄰交換，也就是沒有先後限制。此問題等價於topological sorting！

延伸閱讀：activity network（PERT network）

接下來介紹拓樸順序的實際應用範例。

專案管理領域，經常需要規劃大量工作，這些工作有著工作時間限制、工作先後限制，可以畫成「活動網路」。

然後規劃一套總時程最短的工作方式，並且畫成「甘特圖」。最常用的方法是「關鍵路徑法」，然而它是人工作業的方法。現在請你設計電腦演算法，取代人工作業。

UVa 452 10461 506