convex hull

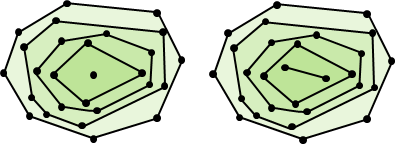
中譯「凸包」或「凸殼」。在高維空間中有一群散佈各處的點，「凸包」是包覆這群點的所有外殼當中，表面積暨容積最小的一個外殼，而最小的外殼一定是凸的。

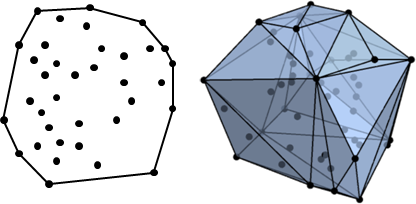
p = RandomInteger[10, {50, 3}]; Show[HighlightMesh[ConvexHullMesh[p], {Style[1, Black, Thick], Style[2, Opacity[0.7]]}], Graphics3D[{PointSize[0.03], Point[p]}]]

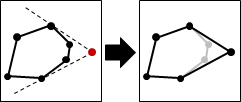
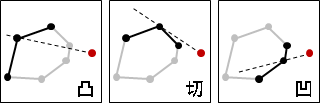
至於「凸」的定義是：圖形內任意兩點的連線不會經過圖形外部。「凸」並不是指表面呈弧狀隆起，事實上凸包是由許多平坦表面組成的。

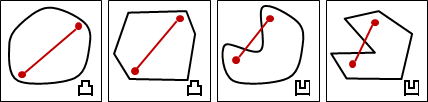
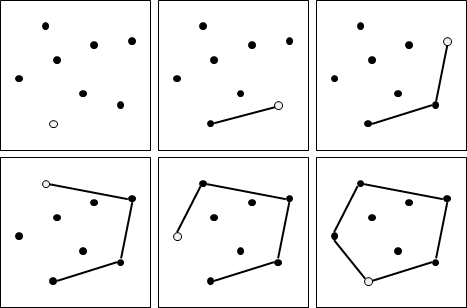
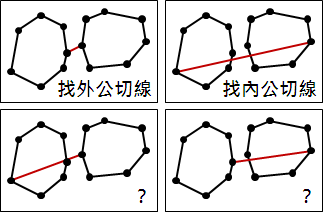
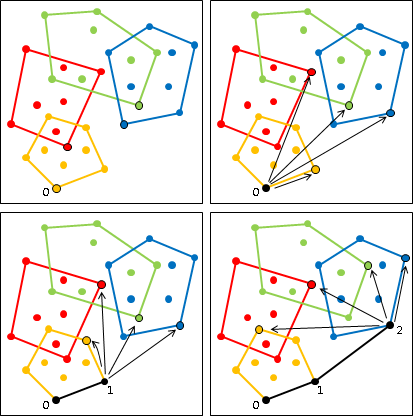
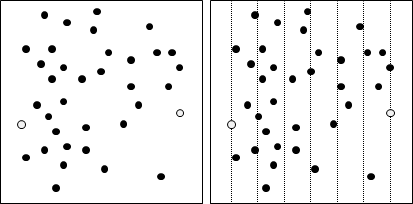
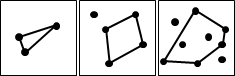
以下討論比較簡單的情況：替二維平面上散佈的點，找到凸包。

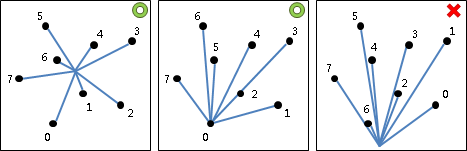
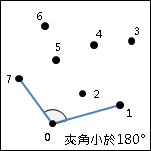
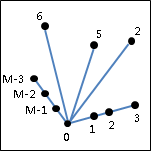
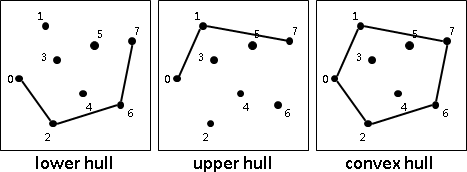
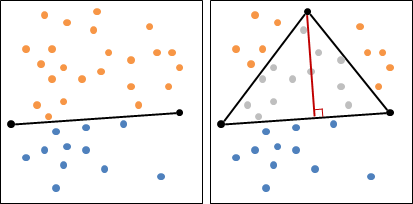
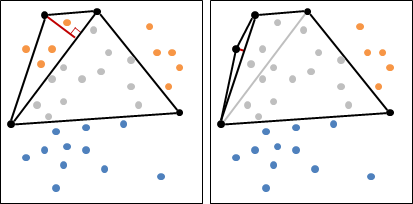
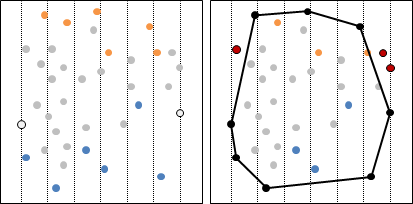
二維平面上的凸包是一個凸多邊形，在所有點的外圍繞一圈即得凸包。另外，最頂端、最底端、最左端、最右端的點，一定是凸包上的點。

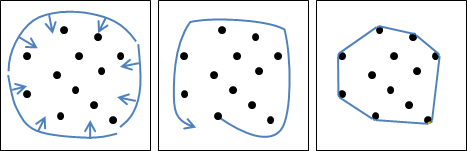
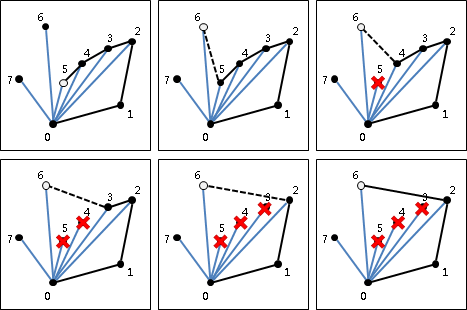
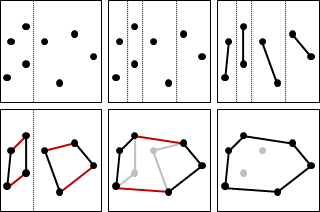
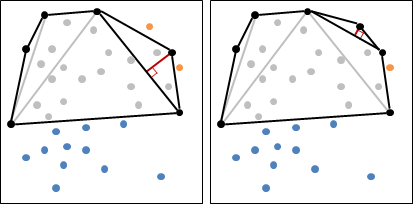
計算凸包時需考慮一些特殊情況：一、凸包上多點重疊；二、凸包上多點共線；三、凸包呈一條線段、一個點、沒有點。通常我們會簡化資訊，以最少的點來記錄凸包，去掉重疊、共線的點。

UVa 109 132 218 361 596 675 681 811 819 10002 10065 10078 10135 10173 10256 10625 11168 11626 ICPC 4450

UVa 802 10089 ICPC 7585

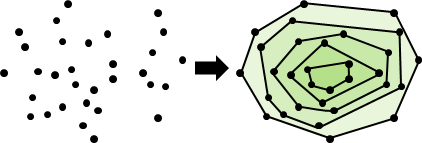
任意圖形的凸包

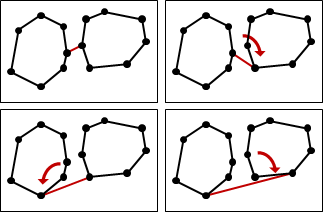
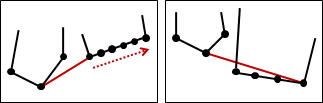
任意圖形都能求出凸包。例如一個多邊形的凸包、大量三角形的凸包、大量線段的凸包。這些問題都可以簡化為一群點的凸包。

圓形、曲線的凸包，我們以下不討論。

convex hull: Jarvis' march (gift wrapping algorithm)

演算法

從一個凸包上的頂點開始，順著外圍繞一圈，順時針或逆時針都可以。

每當尋找下一個要被包覆的點，則窮舉平面上所有點，找出最外圍的一點來包覆。可以利用叉積運算來判斷。

時間複雜度O(NM)，N為所有點的數目，M為凸包的頂點數目。

// P為平面上散佈的點。設定為10點。
// CH為凸包上的頂點。設定為逆時針方向排列。
struct Point {int x, y;} P[10], CH[10];

// 小於。用以找出最低最左邊的點。
bool compare(Point a, Point b)
{
	return (a.y < b.y) || (a.y == b.y && a.x < b.x);
}

// 向量OA叉積向量OB。大於零表示從OA到OB為逆時針旋轉。
int cross(Point o, Point a, Point b)
{
	return (a.x - o.x) * (b.y - o.y) - (a.y - o.y) * (b.x - o.x);
}

// 兩點距離的平方
int length2(Point a, Point b)
{
	return (a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y);
}

// 以o點作為中心點，a點比較遠，b點比較近。
bool far(Point o, Point a, Point b)
{
	return length2(o, a) > length2(o, b);
}

void Jarvis_march()
{
	// 起點必須是凸包上的頂點。這裡用最低最左邊的點作為起點。
	int start = 0;
	for (int i=0; i<10; ++i)
		if (compare(P[i], P[start]))
			start = i;

// 記錄起點
	int m = 0;			// m為凸包頂點數目
	CH[m] = P[start];	// 記錄起點

// 開始包覆，逆時針順序。
	int current = start;	// 當前點
	for (int m=1; true; ++m)
	{
		// 尋找下一個要被包覆的點：
		// 一、找出最外圍的一點。
		// 二、若凸包上多點共線，則找最遠的一點。
		int next = current;
		for (int i=0; i<10; ++i)
		{
			int c = cross(CH[m-1], P[i], P[next]);
			if (c > 0 ||
				c == 0 && far(CH[m-1], P[i], P[next]))
				next = i;
		}

if (next == start) break;	// 繞一圈回到起點了
		CH[m] = P[next];			// 記錄方才找到的點
		current = next;				// 前往下一點
	}
}

實作時請多多運用指標、索引值，儘量避免搬動原本資料。此處的程式碼是不良示範，僅供參考。

如果想找出凸包上重疊的點與共線的點，則改為尋找離上一點最近的點，並且標記目前已包過的點。

convex hull: Graham's scan

演算法

由前面章節可知：凸包上的頂點很有順序的沿著外圍繞行一圈，這個順序是時針順序。

Graham's scan嘗試先將所有點依照時針順序排好，再來做繞行一圈的動作，繞行途中順便掃除凸包內部的點，如此就不必以窮舉所有點的方式來尋找最外圍的點。

要讓所有點依照時針順序排好，只要將中心點設定在凸包內部或者凸包上，然後讓各點依照角度排序即可。如果把中心點設定在凸包外部，結果就不見得是時針順序了。包覆時必須按照時針順序，才能確保結果正確。

一般來說，選擇凸包上的頂點當作中心點是比較好的，因為角度排序時的夾角皆小於180°，可以使用叉積運算來排序（大於180°叉積得負值、等於180°叉積等於零，導致排序錯誤）。另一個好處是，中心點也可以作為包覆的起點。

角度排序時，遇到角度相同的情況，要小心排序。通常是讓距離中心點較近的點排前面。也可以排後面，但是不能亂排。

掃除的過程當中，經常株連許多點。使用stack資料結構來儲存凸包，逐一判斷stack頂端的點，逐一彈出凹陷的點。凹陷的點必定不是凸包上的頂點。

// P為平面上散佈的點。設定為10點。
// CH為凸包上的頂點。設定為逆時針方向排列。可以視作一個stack。
struct Point {int x, y;} P[10+1], CH[10+1];

// 向量OA叉積向量OB。大於零表示從OA到OB為逆時針旋轉。
int cross(Point o, Point a, Point b)
{
	return (a.x - o.x) * (b.y - o.y) - (a.y - o.y) * (b.x - o.x);
}

// 小於。用以找出最低最左邊的點。
bool compare_position(Point a, Point b)
{
	return (a.y < b.y) || (a.y == b.y && a.x < b.x);
}

/*
// 小於。以P[0]當中心點做角度排序，角度由小排到大（即逆時針方向）。
// 角度相同時，順序隨便。
bool compare_angle(Point a, Point b)
{
	return cross(P[0], a, b) > 0;
}
*/

// 小於。以P[0]當中心點做角度排序，角度由小排到大（即逆時針方向）。
// 角度相同時，距離較離中心點較近的點排前面。
bool compare_angle(Point a, Point b)
{
	// 加入角度相同時，距離長度的判斷。
	int c = cross(P[0], a, b);
	return c > 0 || (c == 0 && length2(P[0], a) < length2(P[0], b));
}

void Graham_scan()
{
	// 這裡用最低最左邊的點作為起點，並將中心點換到第零點。O(N)
	swap(P[0], *min_element(P, P+10, compare_position));

// 其餘各點依角度排序。O(NlogN)
	sort(P+1, P+10, compare_angle);

// 直接把中心點作為起點，開始包覆，逆時針方向。O(N)
	P[N] = P[0];	// 讓程式方便處理包至最後一點的情況。

int m = 0;		// m 為凸包頂點數目
	for (int i=0; i<=10; ++i)
	{
		// 掃除凹陷的點
		while (m >= 2 && cross(CH[m-2], CH[m-1], P[i]) <= 0) m--;
		// 添加新的點
		CH[m++] = P[i];
	}

m--;	// 最後一個點是重複出現的起點，故要減一。
}

如果想找出凸包上重疊的點、共線的點，必須特別小心處理剛開始包、快包好時那些重疊的點、共線的點。一種解決方式是：從最低最左點開始，分頭往左右兩邊包，包至最高最右點。相當麻煩。

至於凸包退化成線段或點的情況，則更難解決，此處不討論。

總而言之，此演算法無法漂亮的解決多點共線的情況。

時間複雜度

尋找起點O(N)。排序O(NlogN)。包覆O(N)：總共前進N次，最多倒退N次，一共2N次。

總時間複雜度O(NlogN)，主要取決於排序的時間。

星狀多邊形

星狀多邊形（star-shaped polygon）的定義是：多邊形內部存在一個點，可以看到整個多邊形內部。

也就是說，星狀多邊形可以直接依照連接順序包覆，不必再做角度排序。

convex hull: Andrew's monotone chain

演算法

前面章節採用時針順序，此處改為座標順序。以X座標大小排序，當X座標相同則以Y座標大小排序。

先從起點開始，按照順序掃描，找到下半凸包。再從終點開始，按照相反順序掃描，找到上半凸包。合起來就是完整的凸包。

一口氣解決了凸包有重疊的點、共線的點、退化成線段和點的情況，是相當優美的演算法。

時間複雜度

排序O(NlogN)。包覆O(N)。總時間複雜度O(NlogN)。

單調多邊形

單調多邊形（monotone polygon）的定義是：多邊形可以切開成兩條單調鏈，投影到特定直線上，位置已經排序。

也就是說，單調多邊形可以直接依照連接順序包覆，不必再做座標排序。但是需要事先知道兩條鏈的起點和終點。

convex hull: incremental method

演算法

這是online演算法，隨時維護一個凸包。每當輸入一點，如果此點在凸包內部就直接捨棄；不然就計算此點與當前凸包的兩條切線，然後更新凸包。

要找切線，窮舉切點即可。切點的左右鄰點位於切線同側，判斷僅需O(1)時間。要小心切線與邊重疊的情況。

凸包的資料結構採用circular list，找到兩個切點後，移除其間的連續凹點僅需O(1)時間。總時間複雜度O(N²)。

改進

想要找到新凸包，直接窮舉新凸包的頂點不就好了？

以試誤法嘗試舊凸包的每個頂點。以當前輸入點為基準，若為凸面、切點，則留下；若為凹面，則捨棄。最後就得到新凸包。

如此一來就不需要特殊資料結構了。時間複雜度O(N²)。

即時排序

以當前輸入點為基準，切點的一側是凸面，另一側是凹面，切點恰為凹凸分際。故可用binary search找切點。

凸包的資料結構可以採用splay tree，找切點、移除連續頂點的均攤時間複雜度是O(logN)。總時間複雜度O(NlogN)。

splay tree作排序時，可以參考凸包最左下點，以角度排序。

預先排序

預先按照XY座標排序所有點（平移的掃描線），此演算法即是Andrew's monotone chain，時間複雜度O(NlogN)。

預先排序之後，當前輸入點必在凸包外部（點不重複時）、必有兩條切線。

預先隨機排列

隨機排列、排序，兩者概念相反。

預先隨機排列所有點，則第i回合固定新增兩點、平均掃描N/i點，平均時間複雜度O(NlogN)。推廣到三維空間仍然如此。

convex hull: divide-and-conquer method

演算法

一開始將所有點以X座標位置排序。
divide：將所有點分成左半部和右半部。
conquer：左半部和右半部分別求凸包。
combine：將兩個凸包合併成一個凸包。

合併凸包，找到兩條外公切線即可。從左凸包最右點、右凸包最左點開始，固定左端順時針轉、固定右端逆時針轉，輪流前進直到卡死，就得到下公切線，時間複雜度O(N)。

注意到，下公切線並不見得是左右兩凸包的最低點連線，所以就算一開始抓的是左右凸包的最低點，運氣不好時，仍需要O(N)時間才能找到下公切線。況且抓最低點有可能已經衝過頭了。

附帶一提，內公切線也可如法炮製，改為從左凸包最左點、右凸包最右點開始。如果一個取內側、一點取外側，找公切線有可能衝過頭。

正確性證明：找外公切線的過程中絕對不會與兩凸包相交、找內公切線的過程中一定會與兩凸包相交，卡死時即是相交與不相交的分際，分際即是公切線。

時間複雜度

排序O(NlogN)。分治法O(N)。總時間複雜度O(NlogN)。

分治法當中，遞迴深度O(logN)，合併凸包O(N)，相乘之後得到O(NlogN)。然而凸包內部的點不必用上；找公切線途中遭遇的點，往後不必用上；每個點只用一次，總共應為O(N)。

不預先排序

一開始可以不必排序，只要把所有點分成兩等份即可。兩個凸包合併成一個凸包時，兩個凸包可能會重疊，仍然可以用O(N)時間解決，不過演算法較複雜，此處省略之。

convex hull: Chan's algorithm

演算法

原理是trial and error與divide-and-conquer method。

一、假設凸包最多有M個點。
二、使用試誤法，依序嘗試2^(2^0)、2^(2^1)、2^(2^2)、……這些數值作為M。
　甲、每M個點為一組，所有點被分作⌈N/M⌉組。
　　　O(N)。
　乙、每一組各自求凸包，一共得到⌈N/M⌉個凸包。《Graham's scan》
　　　O(MlogM ⋅ ⌈N/M⌉) = O(NlogM)。
　丙、嘗試求出這些凸包的凸包。《Jarvis' march》
　　　O(3 ⋅ ⌈N/M⌉ ⋅ M) = O(N)。
　　子、每個凸包各用一個指標，指著各自的最低點。
　　　　O(N)。
　　丑、找出所有凸包的最低點，從最低點開始包覆。
　　　　O(N)。
　　寅、每當尋找下一個要被包覆的點：
　　　回、各凸包各自找出最靠外面的一點，一共得到⌈N/M⌉個點。
　　　　　由指標處繼續往後找，指標只進不退。要預覽下一點。
　　　　　O(3 ⋅ ⌈N/M⌉)，均攤。
　　　回、再從這⌈N/M⌉個點當中，看看哪一點最靠外面。
　　　　　O(⌈N/M⌉)。
　　卯、若包了M個點還未形成凸包，則馬上停止，回到步驟二！
　　　　如果途中形成凸包，即是正解。演算法結束。

時間複雜度

步驟二的時間複雜度是O(NlogM)，M每次都不同。對M進行試誤時，謹慎的選擇M的數值，可以將所有步驟二的時間複雜度總和，強壓在O(NlogM)以內。

對M進行試誤時，
用0、1、2、……、M，整體的時間複雜度：
O(Nlog0 + Nlog1 + Nlog2 + ... + NlogM) = O(N ⋅ logM ⋅ M)

用2⁰、2¹、2²、……、M，整體的時間複雜度：
O(N⋅0 + N⋅1 + N⋅2 + ... + NlogM) = O(N ⋅ logM ⋅ logM)

用2^2⁰、2^2¹、2^2²、……、M，整體的時間複雜度：
O(N⋅1 + N⋅2 + N⋅4 + ... + NlogM) = O(N ⋅ logM)

用N，直接就找到答案，不過整體的時間複雜度，不是我們所要的：
O(NlogN)

選擇M的原理，其實就是「倍增搜尋」。

總時間複雜度O(NlogM)，N為所有點的數目，M為凸包的頂點數目，是當今時間複雜度最低的演算法。然而實際執行起來，比先前介紹的演算法都來得慢。

只有理論上的價值，沒有實務上的價值。

convex hull: quick hull algorithm

演算法

一、找出最左點與最右點，連線，所有點分為上半部與下半部。
　　上半部與下半部分開求解。
二、處理上半部，找出上半凸包：
　甲、找出距離底線最遠的點，形成一個三角形區域。
　　　（如果有許多點，就找最靠近左端點的那一點。避免凸包上多點共線。）
　乙、運用叉積運算，找出三角形外部的點，分為左、右兩份。
　　　至於三角形內部、三角形上的點，不會是凸包頂點，盡數剔除之。
　丙、左、右兩份分別遞迴求解，直到找出上半凸包。
　　　三角形的兩翼，分別作為左、右兩份的底線。
三、處理下半部，找出下半凸包。

時間複雜度

時間複雜度O(N²)。然而實際執行起來，比先前介紹的演算法都來得快。實務上最好的凸包演算法！

此演算法的好處：預先剔除凸包內部大部分的點，而且不必預先排序所有點。

排序的時間複雜度O(NlogN)，空間複雜度O(N)。當點的數量很大，例如一千萬，時間約是一千萬的23倍。若記憶體不足，必須採用外部排序，就需要更多時間。

此演算法一開始掃描三遍所有點，找出最左點與最右點、距離底線最遠的點、三角形外部的點，時間約是一千萬的3倍。如果三角形外部的點很少，例如一百萬點，那麼接下來的步驟得以節省許多時間。因此，總時間通常遠低於一千萬的23倍。

遞迴呼叫函數很花時間。當遞迴一兩次後，點數變少，此時可以直接套用其他凸包演算法，節省時間，例如Andrew's monotone chain。

convex hull: Bentley–Preparata–Faust algorithm

演算法

近似演算法。節省更多時間，但是答案可能不對！

一、找出最左點、最右點。
二、水平方向K等分，形成K個等距區間。
三、所有點依照區間歸類。《flash sort》
四、每個區間，找出最低點、最高點。
五、最低點、最左點、最右點，找出下半凸包。
　　最高點、最左點、最右點，找出上半凸包。
　　《Andrew's monotone chain》

時間複雜度

時間複雜度O(N+K)，主要取決於排序的時間。

此演算法一開始掃描一遍所有點，找到最左點與最右點，以及K個區間的最高點與最低點。保留2K+2個點，剔除其他的點。

接著掃描一遍剩下的點，找到偽凸包。

水平距離誤差

預先剔除太多點，其中也剔除了一些真凸包頂點。

所幸距離不會相差太多。真凸包頂點與偽凸包頂點的水平距離，不會超過區間寬度。

所幸距離可以控制範圍。控制區間數量，以控制區間寬度，以控制水平距離誤差。

直線距離誤差

水平方向、垂直方向分別實施演算法。兩個偽凸包合併成一個偽凸包。如此即可同時控制水平距離誤差、垂直距離誤差。然後利用勾股定理得到直線距離誤差。

convex hull: Kirkpatrick–Seidel algorithm

演算法

只有理論上的價值，沒有實務上的價值。

 Yu-Han 說道：
 2014/1/11 at 9:00
 
分享一下最近看到的技巧 – “marriage-before-conquest"
在做Divide and conquer中，遞迴求解的部份解答可以用來加速剩下的計算。

一個簡單的例子是
http://www.geeksforgeeks.org/sorted-linked-list-to-balanced-bst/
把已排序的單向鏈結串列轉成平衡的二元搜尋樹。

如果是用很直接的找中點然後分半遞迴求解，
時間複雜度是O(n lg n)，
但是實際上建立完左半邊的時候，就可以直接得到中點，
因此就可以使得時間複雜度降為O(n)。

一個稍困難的例子是，給定二維空間中的點集合S，
我們稱點p為S中的maxima，
如果在S中沒有任何點的x座標以及y座標同時都大於點p的x座標與y座標。
問題是要把所有maxima找出來。

基於Divide and conquer的技巧，利用x座標等分成兩半分別找出maxima，
然後把在子問題中是maxima但是在考慮整體時不是maxima的點刪除，
如此的時間複雜度可達到O(n lg n)。

使用marriage-before-coquest的技巧，
可以把時間複雜度降到O(n lg h)，h為maxima的個數。
方法是先計算右半邊的maxima，
然後利用右半邊的maxima把左半邊中不可能成為全體的maxima的點先刪除，
最後才計算左半邊。

同樣的技巧也可以用在convex hull上達到O(n lg h)的時間複雜度。

 Yu-Han 說道：
 2014/1/11 at 23:51

以convex hull為例子的話，
是prune-and-search和marriage before conquest的綜合應用。
當有了右半邊的convex hull的點，要刪除左半邊不可能為convex hull的點時，
需要使用一次規劃（利用prune-and-search），
或是自己設計一個prune-and-search的方法。
所以marriage before conquest和prune-and-search是不同的技巧。

除了這三個例子之外，我也找不太到其他marriage-before-conquest的範例了。

convex hull of simple polygon: Melkman's algorithm

演算法

求出一簡單多邊形的凸包。

時間複雜度O(N)。是相當優美的演算法。

convex layers

convex layers（onion）

由外往內，一層一層的凸包，每一層都是一個convex layer。全部的convex layer合稱為一個「洋蔥」。

最內部的convex layer可能退化成一個點或是一條線段。

演算法

使用Jarvis' march一直繞圈，時間複雜度O(N²)。

排序所有點之後，不斷找出剩餘諸點的凸包，最多找O(N)次凸包。可以採用Graham's scan或者Andrew's monotone chain。總時間複雜度O(NlogN) + O(N²) = O(N²)。

ICPC 3655

Erdős–Szekeres conjecture

Erdős–Szekeres conjecture（happy ending problem）

平面上任意2ᴺ + 1個頂點（不會多點共線），是否能描出一個有N+2個頂點的凸多邊形。例如任意三個點可以描出凸三角形，任意五個點可以描出凸四邊形，任意九個點可以描出凸五邊形，以此類推。

Szekeres發表了這個猜想之後，有一位女數學家證明了N更大的情形，兩人因而相知相遇、結為連理，有了幸福快樂的結局。因此Erdős暱稱此猜想為happy ending problem。

註：Erdős–Szekeres theorem是另外一件事情，與Erdős–Szekeres conjecture不同。

2ᴺ個數字，任何一種排列，
必能形成長度為N+1的「先遞增、再遞減子序列」。

這個命題曾經用來證明此猜想，不過結果是失敗的。

目前來說，凹與凸是無法量化的，凹與凸無法全體一起比較、全體一起排序。即便是凸包演算法，也只能局部逐一判斷凹凸。

用長度來衡量凹凸乍看是個不錯的點子，不過困難重重，可能不是一個好方向。

最後附上此命題的證明。

2^(N-2)個數字，任何一種排列，
必能形成長度為N-1的「先遞增、再遞減子序列」。

數學歸納法。

當N=2時，一個數字的任何一種排列，
都可以形成一個長度為1的「先遞增、再遞減子序列」。

當N=3時，兩個數字的任何一種排列，
都可以形成一個長度為2的「先遞增、再遞減子序列」。
例如12，剛好都是遞增。
例如21，剛好都是遞減。
例如11，說是遞增或是遞減都可以。

假設N=k時成立。
則N=k+1時，
我們將2^(k-1)個數字的隨便一個排列，中間切一刀，等分為左半和右半。
左半、右半各自都可以形成長度為k-1的「先遞增、再遞減子序列」。

左半「先遞增、再遞減子序列」的最後一個數字，叫做p，
右半「先遞增、再遞減子序列」的第一個數字，叫做q，
如果p > q，則左半與q可形成長度為k的「先遞增、再遞減子序列」。
如果p < q，則p與右半可形成長度為k的「先遞增、再遞減子序列」。
如果p = q，則上述兩種情形任意一種皆可。
得證。