matching

一張無向圖，相鄰兩點配成一對。但是呢 —— 一個點最多只能與一個鄰點配成一對，寧可孤家寡人，不可三妻四妾。雙雙對對的邊，整體形成一個「匹配」。

換句話說：挑選一些邊，讓圖上每一點僅接觸零條邊或一條邊。這些邊構成的集合，稱作一個「匹配」。

matched vertex 與 unmatched vertex

一個點要嘛跟另一個點比翼雙飛，要嘛孑然一身 ── 前者為「匹配點」，後者為「未匹配點」。

matched edge 與 unmatched edge

出雙入對的兩點之間的邊為「匹配邊」，除此以外則為「未匹配邊」。一個匹配由許多匹配邊組成。

cardinality

一個匹配擁有的匹配邊數目，稱作「基數」。

「基數」源自集合論，意義是集合的大小。

順便介紹一些特別的匹配：

maximal matching
一張圖中，沒有辦法直接增加配對數的匹配。

maximum matching
一張圖中，配對數最多的匹配。也是maximal matching。

perfect matching
一張圖中，所有點都送作堆的匹配。也是maximum matching。

weight

當圖上的邊都有權重，一個匹配的權重是所有匹配邊的權重總和。

順便介紹一些特別的匹配：

maximum weight matching
一張圖中，權重最大的匹配。

maximum weight maximum (cardinality) matching
一張圖中，配對數最多的前提下，權重最大的匹配。

maximum weight perfect matching
一張圖中，所有點都送作堆的前提下，權重最大的匹配。

bipartite graph

「二分圖」是圖的一種特例。一張二分圖的結構是：兩群點（通常標記作 X 集合與 Y 集合）、橫跨這兩群點的邊（ X 與 Y 之間）。至於兩群點各自之內是沒有邊的（ X 與 X 、 Y 與 Y 間）。

順帶一提，二分圖構造較單純，其資料結構可以進行精簡：

bipartite matching

一張二分圖上的匹配，稱作「二分匹配」。所有的匹配邊，都是這橫跨這兩群點的邊，就像是連連看。

使用 flow 尋找 matching

一側接上源點，另一側接上匯點，即可利用網路流，解決最大二分匹配問題、最大（小）權二分匹配問題。

使用 matching 尋找 path

利用最小權二分匹配，解決有向圖的點到點最短路徑問題。但是圖上不得有負環。

所有點拷貝一份，所有邊形成二分圖。相同的點追加零邊（中繼點），一側去除終點以及連出的邊，另一側去除起點以及連入的邊。

一、額外建立二分圖：
　點：X側、Y側都有V個點。
　邊：若原圖有一條i點到j點的有向邊，
　　　則二分圖就有一條Xi點到Yj點的邊。
二、點到點最短路徑問題：
　口、增加Xi點到Yi點的邊，權重設為零。
　口、Y側，去掉起點，也去掉連入起點的邊。
　口、X側，去掉終點，也去掉終點連出的邊。
三、計算最小權二分匹配。

一、額外建立二分圖：
　口、拷貝原圖的adjacency matrix。
二、點到點最短路徑問題：
　口、對角線改為零。
　口、去除起點編號的直條。
　口、去除終點編號的橫條。
　　　（最後成為(V-1)×(V-1)矩陣。）
三、計算最小權二分匹配。

利用最小權匹配，解決無向圖的點到點最短路徑問題。但是圖上不得有負環。

一、額外建立無向圖：
　點：V個原來的點，再加上V個複製的點。
　邊：若原圖有一條i點到j點的無向邊，
　　　則新圖就有：
　　　一條i 點到j 點的無向邊、
　　　一條i'點到j 點的無向邊、
　　　一條i 點到j'點的無向邊、
　　　一條i'點到j'點的無向邊。
二、轉化問題：
　口、增加i點到i'點的無向邊，權重設為零。
　口、去掉起點，也去掉連著該點的邊。
　口、去掉終點的複製點，也去掉連著該點的邊。
三、計算最小權匹配。

導讀

augmenting path theorem 是尋找最大匹配的重要理論。本章節當中，首先介紹相關元件，然後證明理論，最後提出一種尋找最大匹配的手段。

alternating path 與 alternating cycle

「交錯路徑」與「交錯環」。在一張存在匹配的圖上，匹配邊和未匹配邊彼此相間的一條路徑與一個環。

交錯環有個有趣的特性：顛倒交錯環上的匹配邊和未匹配邊，可以改變匹配，但是不影響 cardinality 。

augmenting path

「擴充路徑」。一條交錯路徑，第一個點和最後一個點都是未匹配點。因此第一條邊和最後一條邊都是未匹配邊。

擴充路徑有個更有趣的特性：顛倒擴充路徑上的匹配邊和未匹配邊，可以改變匹配，並且讓 cardinality 加一。

symmetric difference

兩個集合 A 和 B 的「對稱差集」定義為 A⊕B = (A∪B) - (A∩B) 。例如 A = {1,3,4,5} 、 B = {2,4,5,7} 、 A⊕B = {1,2,3,7} ，沒有重複出現的元素將會留下，重複出現的元素將會消失。

對稱差集非常適合用來描述「顛倒擴充路徑上的匹配邊與未匹配邊」這件事情。現在有一個匹配 M ，和一條擴充路徑 P （拆開成邊），那麼 M⊕P 會等於新匹配。

坊間書籍常以對稱差集來表述匹配相關理論。在此特別將對稱差集的概念介紹給各位，希望各位往後遇到 ⊕ 這個符號時，不會下意識地認為它艱深晦澀。

symmetric difference of matchings

同一張圖上的兩種匹配 M 和 M* 也可以計算對稱差集 M⊕M* ，總共會產生六大類 connected component ，都是交錯路徑或者交錯環，各位若是不信可以親自實驗看看：

兩個匹配的對稱差集，提供了這兩個匹配互相變換的管道：對其中一個匹配來說，只要顛倒整個對稱差集當中的匹配邊與未匹配邊，就變成另一個匹配。寫成數學式子就是：令 M⊕M* = P ，則 M⊕P = M* 、 M*⊕P = M 。

augmenting path theorem

從圖上任取一個未匹配點，如果找不到以此點作為端點的擴充路徑，那麼這張圖會有一些最大匹配不會包含此點。

更進一步來說，就算從這張圖上刪除此點（以及相連的邊），以剩餘的點和邊，還是可以找到原本那張圖的其中一些最大匹配。

證明不困難，利用一下先前所學到的東西，便可以推理出來：

令當下的匹配M找不到以未匹配點p作為端點的擴充路徑。
令M*是該圖的其中一個最大匹配。
一、如果p不在M*上：
　　刪除此點完全不會對M和M*有任何影響，定理成立。
二、如果p在M*上：
　甲、p對於M來說是未匹配點。理所當然p不在M上。
　乙、考慮M⊕M*的六種情形。p不在M上，且p在M*上，所以只有d或e符合條件。
　丙、M找不到以p作為端點的擴充路徑，所以d不符合條件，只有e符合條件。
　丁、對於M*來說，只要照著e顛倒匹配邊和未匹配邊，
　　　就可以製造出另一個不會包含p的最大匹配，
　　　成為步驟一的情況，定理還是成立。

這個理論相當重要，它表明了一個找最大匹配的手段：

遞歸法，不斷刪除找不到擴充路徑的未匹配點，減小問題規模，減小圖的規模。無論刪除多少點，依然能保留原圖的某些最大匹配。

一、一開始圖上所有點都是未匹配點。
二、每個未匹配點，依序嘗試作為擴充路徑的端點：
　甲、如果找得到擴充路徑：
　　　沿著擴充路徑修改現有匹配，以增加cardinality。
　　　（此未匹配點變成了匹配點。）
　乙、如果找不到擴充路徑：
　　　直接刪除此點。繼續下去仍然可以找到原圖的其中一個最大匹配。
　　　（此未匹配點被刪除。）

所有的未匹配點，要嘛變成匹配點、要嘛被刪除。未匹配點盡數消失，同時產生其中一個最大匹配。

augmenting path theorem 另一種形式

一個匹配，若無擴充路徑，即是最大匹配。

要是圖上所有未匹配點都不能當作擴充路徑的端點，就代表著圖上根本就沒有擴充路徑。 cardinality 無法增加，就代表著當下的匹配就是最大匹配囉！

這個理論相當重要，它表明了一個找最大匹配的手段：

不斷找擴充路徑，直到找不到為止。此時的匹配就是最大匹配。

導讀

以下章節將介紹 matching 的各種演算法。每當講解一個演算法，先談比較簡單的特例 bipartite matching ，再談比較複雜的通例 matching ，循序漸進講解。

用途

找出一張二分圖的其中一個最大二分匹配。

alternating tree

選定一個未匹配點作為起點，嘗試列出所有的交錯路徑 ── 藉此尋找擴充路徑。

有個重要的發現：當兩條交錯路徑撞在同一個點，將來還是只能選擇其中一條路徑來進行擴充，所以只要留下一條路徑就夠了。

根據這個重要的發現，圖上的每個點、每條邊只需出現一次。我們得以使用 graph traversal 來尋找一條擴充路徑，並形成一棵樹，稱作「交錯樹」。

二分圖當中，每條交錯路徑都在 X 與 Y 之間來回。

演算法

一、一開始圖上所有點都是未匹配點。
二、X的每個未匹配點，依序嘗試作為擴充路徑的端點。
　　以graph traversal建立交錯樹，以尋找擴充路徑。
　　（X的未匹配點一旦處理完畢，Y的未匹配點不會再有擴充路徑，故只需找X側。）
　甲、如果找得到擴充路徑：
　　　沿著擴充路徑修改現有匹配，以增加cardinality。
　　　（此未匹配點變成了匹配點。）
　乙、如果找不到擴充路徑：
　　　直接刪除此點。繼續下去仍然可以找到原圖的其中一個最大匹配。
　　　（此未匹配點被刪除。）

這個演算法運作起來，如同接上了源點與匯點再進行 Ford–Fulkerson algorithm （ augmenting path algorithm ）。

時間複雜度

時間複雜度是 O(V) 次 graph traversal 的時間。圖的資料結構為 adjacency matrix 是 O(V³) ；圖的資料結構為 adjacency lists 是 O(VE) 。

找出一個最大二分匹配

以 DFS 尋找擴充路徑，程式碼變得相當精簡。

採用 BFS 也是可以的，這裡就不贅述了。

greedy matching

這裡介紹一個加速手段：明顯可以配對的點，預先配對。如此一來這些點就不必建立交錯樹。圖很龐大的時候，得以發揮功效。

雖然多了一次 graph traversal ，但是少了許多棵交錯樹。

UVa 259 670 753 10080 10092 10243 10418 10984 663 11148

用途

找出一張無向圖的其中一個最大匹配。

alternating tree: cross edge

交錯樹當中，「偶點」距離樹根偶數條邊，「奇點」距離樹根奇數條邊。一般圖的交錯樹、二分圖的交錯樹，兩者有個不同之處 ── 偶點到偶點的邊。

二分圖的交錯樹
偶點到奇點：一定是未匹配邊。
奇點到偶點：一定是已匹配邊。
偶點到偶點：二分圖不會有這種邊。
奇點到奇點：二分圖不會有這種邊。

一般圖的交錯樹
偶點到奇點：一定是未匹配邊。
奇點到偶點：一定是已匹配邊。
偶點到偶點：一定是未匹配邊，且會形成「花」。
奇點到奇點：交錯樹不會有這種邊，因為不會形成交錯路徑。

alternating tree: cycle

偶點到偶點的邊，在交錯樹上形成一個環。只要穿越這條偶點到偶點的邊，以繞遠路的方式，環上所有奇點都能夠成為偶點，而且延伸出更多條交錯路徑。

一般圖的交錯樹，多了偶點到偶點的邊，奇點因此活躍了。環上的所有奇點，可以搖身一變成為偶點，然後重新延伸出交錯路徑！

blossom 與 base

在交錯樹上，分岔的兩段交錯路徑，接上一條偶點到偶點的邊，所形成的奇數條邊的環，就稱作「花」。花上兩條未匹配邊的銜接點，則稱作「花托」，宛如花開在交錯樹上。

blossom contraction

既然花上的點都可以成為偶點，那麼乾脆把花直接縮成一個偶點，讓交錯樹更簡潔明白。

交錯樹上可能會有許多偶點到偶點的邊，形成許多朵重重疊疊的花，我們可以用任意順序縮花。實作時，為了容易找到花，可以在建立交錯樹的途中，一旦發現偶點到偶點的邊就立即縮花。一句話，一旦發現花就立即縮花。

縮花的次數呢？一朵花最少有三個點，縮花後成為一個點，前前後後少了兩個點。由此推得： V 個點的圖建立一棵交錯樹，最多縮花 V/2 次；如果再多縮幾朵花，樹上就沒有點了。

路徑沿著花繞來繞去，繞得你暈頭轉向。

演算法

一、一開始圖上所有點都是未匹配點。
二、每個未匹配點，依序嘗試作為擴充路徑的端點，
　　並以graph traversal建立交錯樹，以尋找擴充路徑。
　甲、走到未拜訪過的點：
　　a. 如果是已匹配點，則延伸交錯樹，一條未匹配邊再加一條已匹配邊。
　　b. 如果是未匹配點，則找到擴充路徑。
　乙、走到已拜訪過的點：
　　a. 如果是偶點，形成花。做花的處理。
　　b. 如果是奇點，根據只需留一條路徑的性質，什麼都不必做。

花的處理：
一、找出花托：cross edge兩端點的lowest common ancestor。
二、建立從樹根到花上各奇點之交錯路徑。
　　一定會經過cross edge。小心別重複經過花托。
三、把花上面的點全部當作偶點。
　　或者，乾脆把花直接縮成一個偶點。
　　縮花可用disjoint sets資料結構。

找出一個最大匹配

採用 BFS 建立交錯樹。採用 array 記錄交錯路徑，以大量 array 紀錄交錯樹上每一條交錯路徑。不縮花。

一、 V 個未匹配點分別建立交錯樹。二、一棵交錯樹最多 V 條交錯路徑，一條交錯路徑長度最多 V 條邊。三、一棵交錯樹最多 E 朵花，每朵花需要 O(V) 時間找花托。

時間複雜度 O(V³ + V²E) ，通常簡單寫成 O(V²E) 。

找出一個最大匹配

採用 BFS 建立交錯樹，以 disjoint-sets forest 實作縮花。縮花時，將花托設定為 disjoint-sets forest 的樹根，程式碼比較簡潔。

一棵交錯樹的建立過程當中，縮花縮掉的點不會再度出現。導致尋找花托、也就是 LCA 的總時間複雜度從 O(VE) 降為 O(V+E) 。也導致 merge 與 find 的總時間複雜度從 O(Eα(V)) 降為 O(V+E) 。

時間複雜度是 V 次 graph traversal 的時間。圖的資料結構為 adjacency matrix 是 O(V³) ；圖的資料結構為 adjacency lists 是 O(VE) 。

順帶一提，也可以一口氣把圖上所有未匹配點作為樹根，建立交錯森林。當兩棵交錯樹碰到的時候，就是有擴充路徑了。這麼做可以稍微降低縮花的次數。

greedy matching

先前章節提到的加速手段，此處也適用。

UVa 11439

用途

找出一張二分圖的其中一個最大二分匹配。

演算法

每回合一口氣找出所有的最短擴充路徑們，並且進行擴充，直到找不到為止。最多需要 2sqrtV 回合。證明請參考 CLRS 。

一、一開始圖上所有點都是未匹配點。
二、重複下列動作，直到找不到擴充路徑為止：
　　（最多需要2sqrtV回合。）
　甲、X的所有未匹配點同時作為樹根，
　　　採用BFS建立交錯森林，一層一層延展，
　　　直到發現所有的最短擴充路徑們。
　　　（時間複雜度是一次graph traversal的時間。）
　乙、各個樹根依序往樹葉方向尋找最短擴充路徑。
　　　也可以由樹葉往樹根找。
　　　一旦拜訪過的點就不再拜訪。
　　　（時間複雜度是一次graph traversal的時間。）

這個演算法運作起來，如同接上了源點與匯點再進行 blocking flow algorithm 。

時間複雜度

時間複雜度是 2sqrtV 次 BFS 的時間。圖的資料結構為 adjacency matrix 是 O(V²sqrtV) = O(V^2.5) ；圖的資料結構為 adjacency lists 是 O((V+E)sqrtV) ，通常簡單寫成 O(EsqrtV) 。

找出一個最大二分匹配

用途

找出一張無向圖的其中一個最大匹配。

演算法

每回合一口氣找出所有的最短擴充路徑們，並且進行擴充，直到找不到為止。

時間複雜度

O(EsqrtV) 。

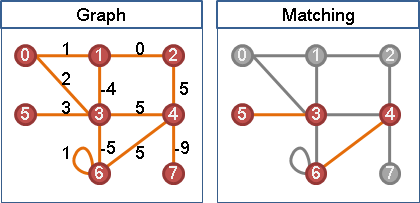
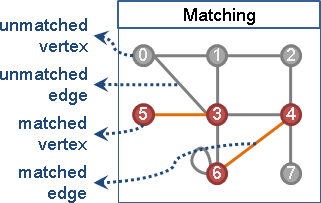
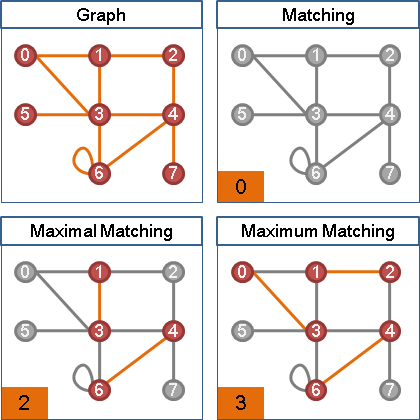
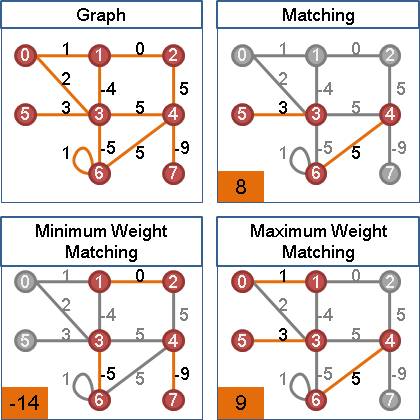
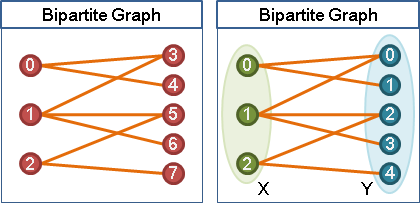
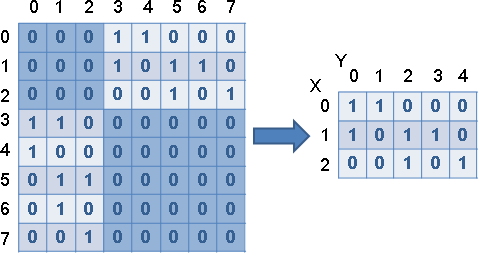
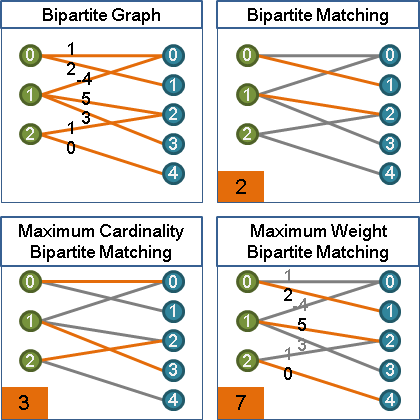
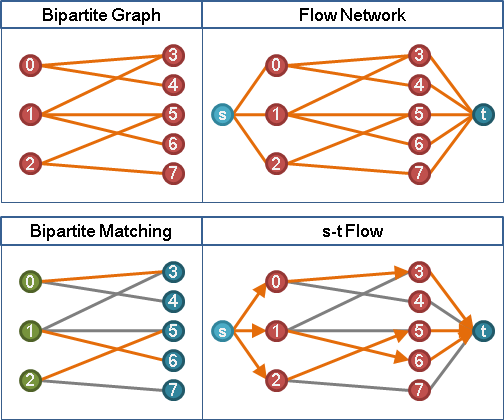
用途

求出一張二分圖的其中一個最大權完美二分匹配。稍做修改，也能求出最大權最大二分匹配、最大權二分匹配，以及最小權版本。

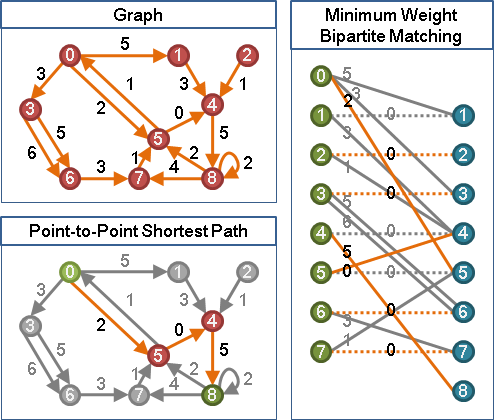
maximum weight bipartite matching
一張二分圖中，權重最大的二分匹配。

maximum weight maximum (cardinality) bipartite matching
一張二分圖中，配對數最多的前提下，權重最大的二分匹配。

maximum weight perfect bipartite matching
一張二分圖中，所有點都送作堆的前提下，權重最大的二分匹配。

調整權重

一個點連接的所有邊，等量增加權重、等量減少權重，都不會影響最大權完美匹配的位置。

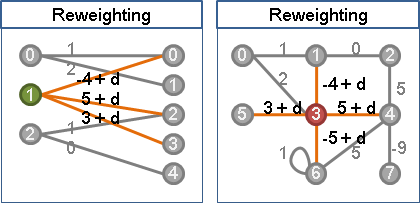
此性質二分圖和一般圖都成立。

建立 vertex labeling

幫各個點都創造一個變數，直接在點上調整權重，代替在邊上調整權重，藉此減少調整權重的時間。

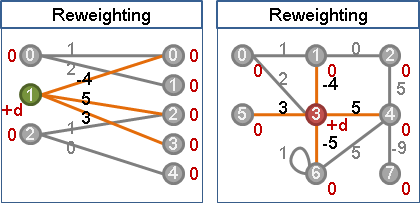
最小化所有點的權重總和 = 最大化所有匹配邊的權重總和

建立一組 vertex labeling ：令圖上每一條邊，其兩端點的權重總和，大於等於邊的權重。

l(x) + l(y) ≥ adj(x,y)

所有點的權重總和，大於等於任意匹配的權重（所有匹配邊的權重總和）。

∑ l(x) ≥ ∑ adj(x,y)
V        M

盡力降低所有點的權重總和，就能逼近最大權完美匹配的權重。

min ∑ l(x) = max ∑ adj(x,y)
    V            M

求出一組總和最小的 vertex labeling ，就能得到最大權完美匹配。

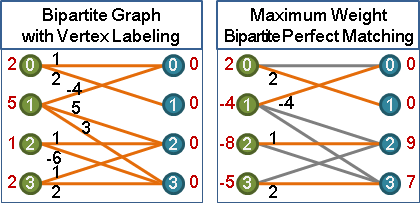
求最大值變成了求最小值，這是很實用的數學轉換。這個轉換有個重要目的：操作 vertex labeling 而不操作 edge labeling ，藉此減少調整權重的時間。

【註：以 linear programming 的觀點來看，這個轉換正是 primal problem 與 dual problem 之間的轉換。】

equality edge （ admissible edge ）

「等邊」。兩端點的點權重相加，恰好等於邊權重。

l(x) + l(y) = adj(x,y)

當 vertex labeling 的總和降低到極限，可以發現最大權完美匹配的所有匹配邊都是等邊。

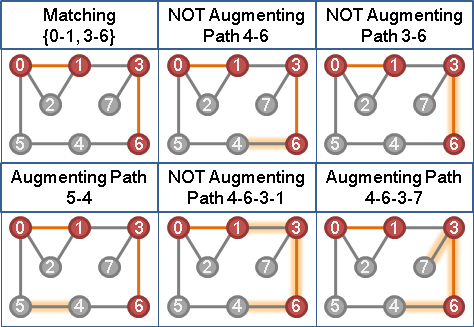
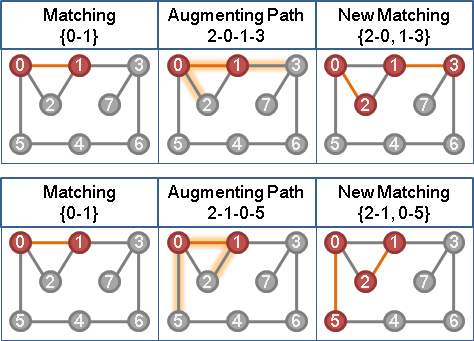
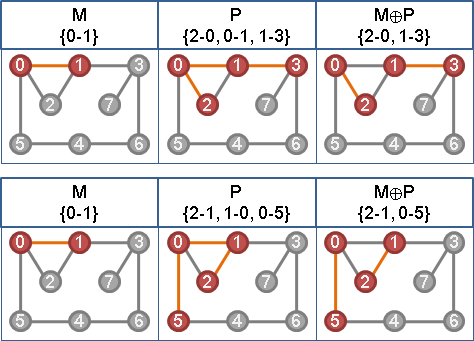
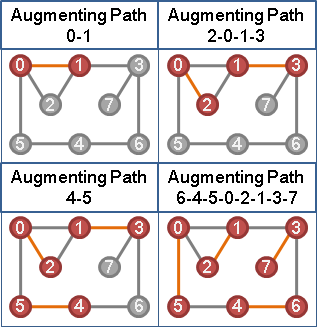
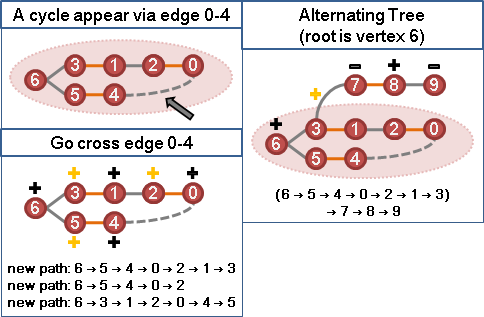
augmenting path algorithm + equality edge

結合擴充路徑與等邊，得到最大權完美匹配演算法。

一、一開始圖上所有點都是未匹配點。
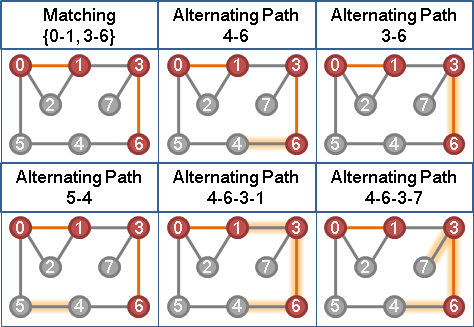
二、每個未匹配點，依序嘗試作為擴充路徑的端點。擴充路徑必須全是「等邊」。
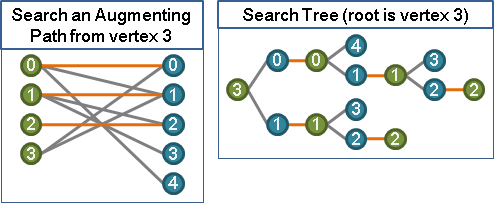
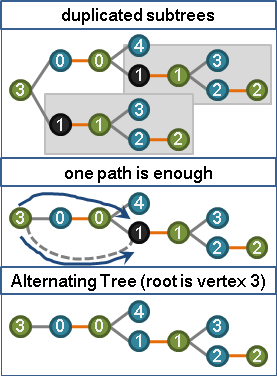
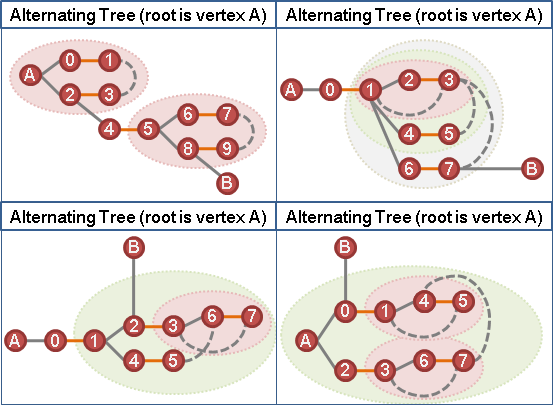
　　以graph traversal建立交錯樹。交錯樹必須全是「等邊」。
　甲、如果找得到「等邊」擴充路徑：進行擴充。
　乙、如果找不到「等邊」擴充路徑：？？？？？

擴充路徑全是等邊，最後得到的最大權匹配當然全是等邊。

當找不到等邊，只好想辦法調整 vertex labeling 了。

調整 vertex labeling

必須維持每一條邊的大於等於性質，而且既有等邊不能動。該如何調整權重呢？

先把等邊交錯樹延伸到極限，再窮舉末梢的非等邊，計算「兩端點的點權重相加、再減掉邊權重」，找到此差值最小者。

d = min { l(x) + l(y) - adj(x,y) }     x為樹上一點、y為樹外一點

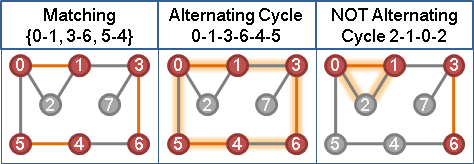
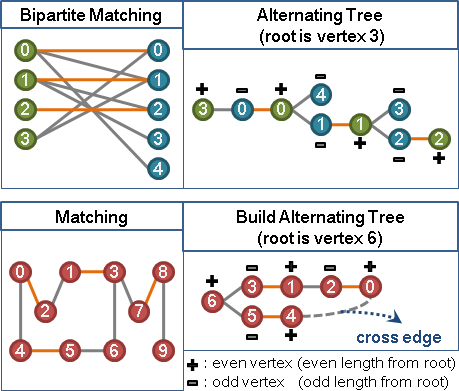
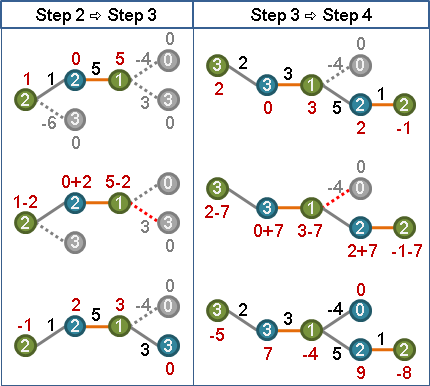
樹上偶點減此值、樹上奇點加此值。一加一減，樹內樹外既有等邊保持不動，樹梢則有一條（以上）非等邊變成了等邊。

l(x) -= d     x為樹上偶點
l(x) += d     x為樹上奇點

如此便製造了一條（以上）的等邊，而且既有等邊保持不動，而且維持了每一條邊的大於等於性質。整張圖的等邊只增不減。

【註：這宛如最短路徑問題的調整權重手法。】

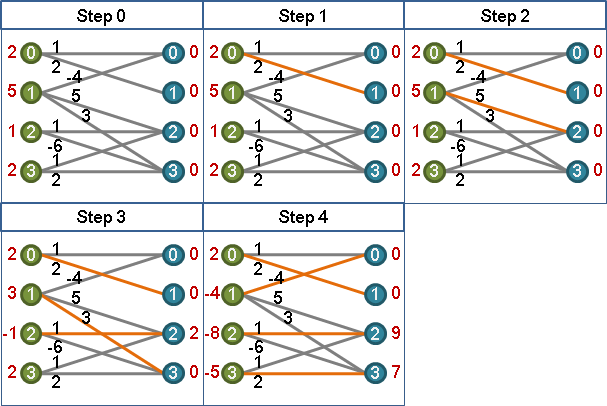
等邊交錯樹宛如最小生成樹，製造等邊宛如 Prim's algorithm ，屢次找不在樹上、讓匹配權重下降最少的等邊。

演算法

一、建立vertex labeling，使之滿足前述的大於等於性質。
二、一開始圖上所有點都是未匹配點。
三、X的每個未匹配點，依序嘗試作為等邊擴充路徑的端點。
　　以graph traversal建立等邊交錯樹。
　　（X的未匹配點一旦處理完畢，Y的未匹配點不會再有擴充路徑，故只需找X側。）
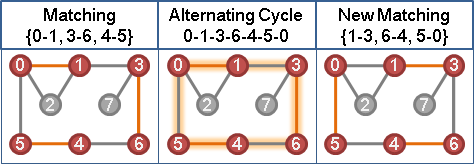
　甲、如果找得到等邊擴充路徑：
　　　沿著等邊擴充路徑修改現有匹配，以增加cardinality。
　乙、如果找不到等邊擴充路徑，則製造新等邊：
　　　等邊交錯樹末梢的非等邊，算最小差值d。（有人稱作slack）
　　　樹上偶點減d，樹上奇點加d。樹梢新增了一條以上的等邊。

找出一個最大權完美二分匹配

一、 V 個未匹配點分別建立交錯樹。二、一棵交錯樹最多 V 點，每次調整權重得以新增一點（以上）。三、每次調整權重之前，需要找到最小差值，最多窮舉 E 條邊。

時間複雜度是三者相乘。圖的資料結構為 adjacency matrix 是 O(V⁴) ；圖的資料結構為 adjacency lists 是 O(VVE) 。

找出一個最大權完美二分匹配

交錯樹的建立過程，宛如最小生成樹的 Prim's algorithm ，宛如最短路徑樹的 Dijkstra's algorithm ，運用各種極值資料結構得以降低時間複雜度。例如建立表格記錄最小差值，時間複雜度降為 O(V³) 。

UVa 11383 1411

最大權最大二分匹配

化作最大權完美二分匹配：假設 X 大 Y 小。 Y 側，補 X-Y 個點、連 X(X-Y) 條零邊。

最大權二分匹配

化作最大權最大二分匹配：最大權二分匹配不必有負邊，預先捨棄圖上所有負邊。

最小權完美二分匹配

化作最大權完美二分匹配：邊權重變號。

演算法

建立等邊交錯樹，額外考慮花。

每當形成花，就把花上所有點標記為偶點，並進行縮花。每當調整權重，偶點減 d 、奇點加 d ，此舉造成花上的每條匹配邊，皆與實際上的權重值少了 2d 。

必須記錄這失去的 2d 。額外建立一組 blossom labeling ，最初為 0 ；每當調整權重，就加減 2d 。

等邊的定義改成：

l(x) + l(y) + ∑ b(B) = adj(x,y)
              包含邊(x,y)的所有花B。

調整權重改成：

d = min { l(x) + l(y) + ∑ b(B) - adj(x,y) }     x為樹上一點、y為樹外一點

l(x) -= d     x為樹上偶點
l(x) += d     x為樹上奇點

b(B) += 2d    B為最外層偶花
b(B) -= 2d    B為最外層奇花

時間複雜度 O(VVE) 。運用各種極值資料結構得以降低時間複雜度。例如建立表格記錄最小差值，時間複雜度降為 O(V³) 。

《 Data Structures for Weighted Matching and Nearest Common Ancestors with Linking 》