「圖」與「道路地圖」

一張圖想像成道路地圖，點想像成地點，邊想像成道路，權重想像成道路的長度。若兩點之間以邊相連，表示兩個地點之間有一條道路，道路的長度是邊的權重。

有時候為了應付特殊情況，邊的權重可以是零或者負數，也不必真正照著圖上各點的地理位置來計算權重。別忘記「圖」是用來記錄關聯的東西，並不是真正的地圖。

path

在圖上任取兩點，分別作為起點和終點，我們可以規劃許多條由起點到終點的路線。一條路線就是一條「路徑」。

如果起點到終點是不通的，那麼就不存在起點到終點的路徑。如果起點和終點一樣，那麼就存在路徑，路徑是一個點、零條邊。

路徑也有權重。路徑經過的每一條邊，沿路加總權重，就是路徑的權重（通常只加總邊的權重，而不考慮點的權重）。路徑的權重，可以想像成路徑的總長度。

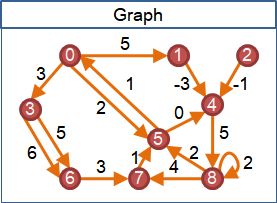
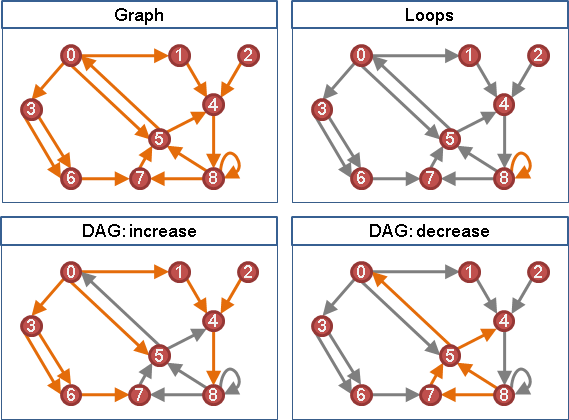
shortest path

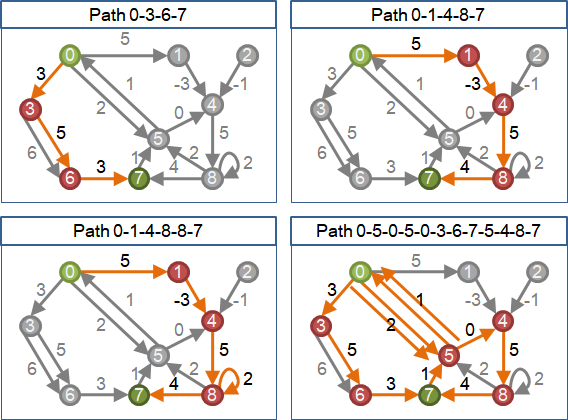
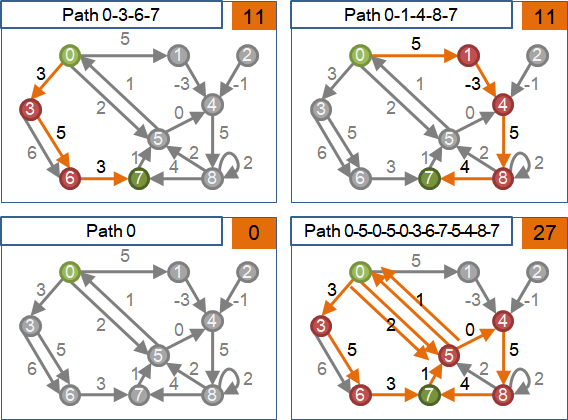
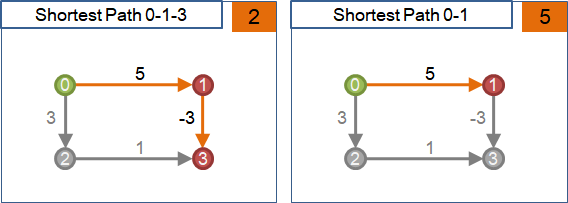
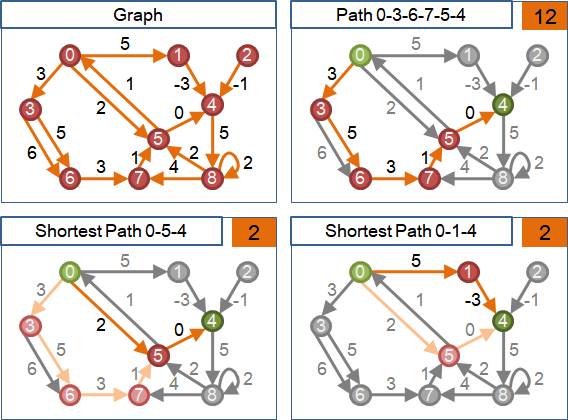
「最短路徑」是由起點到終點、權重最小的路徑，可能有許多條，也可能不存在。起點到終點不通、不存在路徑的時候，就沒有最短路徑。

「最短路徑」不見得是邊最少、點最少的路徑。

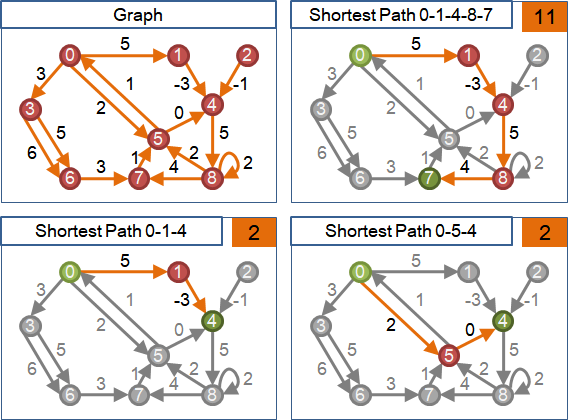
longest path

最長路徑和最短路徑很類似。最長路徑問題當中，每一條邊的權重添上負號，就變成最短路徑問題。反過來也是。

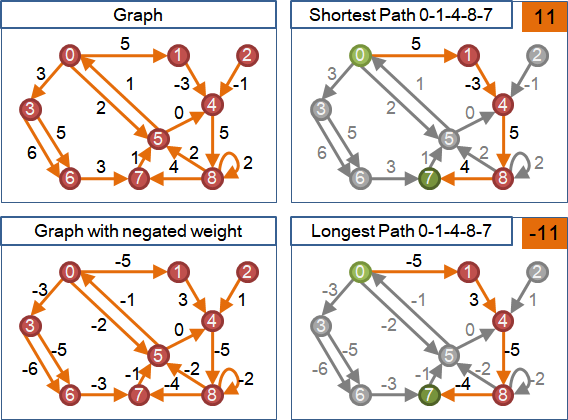
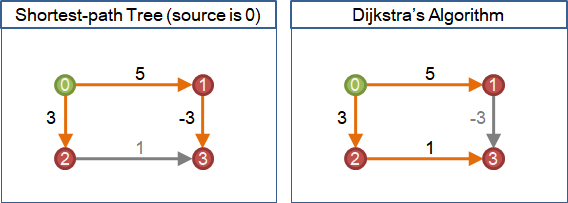
shortest-path tree

最短路徑有一個特別的性質：每一條最短路徑，都是由其它的最短路徑延展而得。一條最短路徑，截去末端之後，還是最短路徑。

提到延展，就聯想到樹！引入延展的概念，最短路徑們得以形成一棵樹。

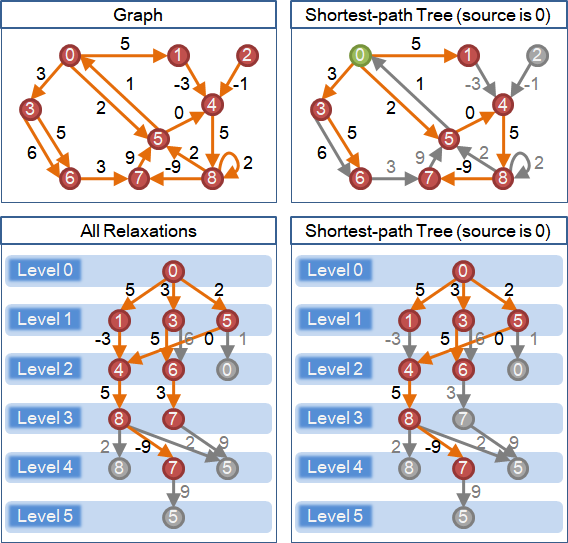
在圖上選定一個起點，由起點到圖上各點的最短路徑們，形成一棵有向樹，稱作「最短路徑樹」。由於兩點之間的最短路徑不見得只有一條，所以最短路徑樹也不見得只有一種。

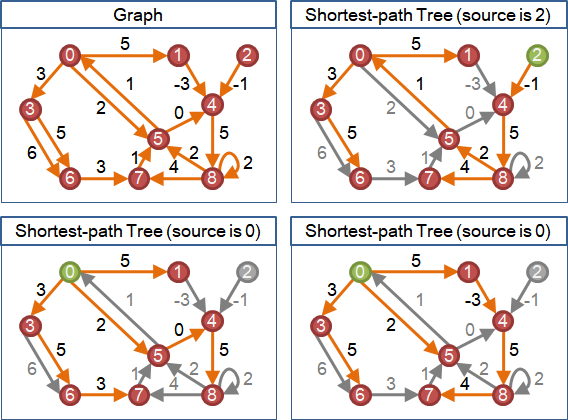
shortest-path graph

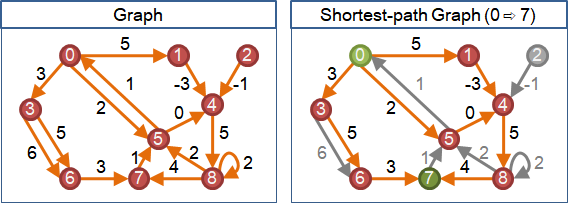
在圖上選定一個起點和一個終點，由起點到終點的所有最短路徑們，形成一張有向圖，稱作「最短路徑圖」，只有唯一一種。

當圖上每一條邊的權重都是正數，最短路徑圖是有向無環圖DAG。

兩點之間有多條邊

當一張圖的兩點之間有多條邊，可以留下一條權重最小的邊。這麼做不影響最短路徑。

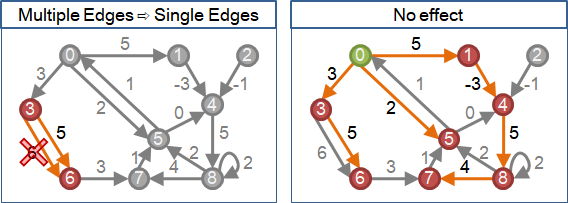
當圖的資料結構為adjacency matrix，任兩點之間只能擁有一個權重值。此時權重值必須設定成權重最小的邊的權重。

兩點之間沒有邊（兩點不相鄰）

當一張圖的兩點之間沒有邊，可以補上一條權重無限大的邊。這麼做不影響最短路徑。

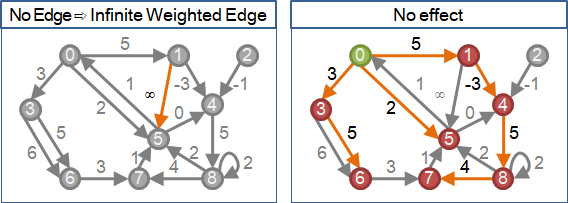
當圖的資料結構為adjacency matrix，任兩點之間一定要有一個權重值。此時權重值必須設定成一個超大數字，當作無限大；不可設定為零，以免計算錯誤。

int w[9][9]; // adjacency matrix void init() { for (int i=0; i<9; ++i) for (int j=0; j<9; ++j) w[i][j] = 1e9; // 設定成一個超大數字 int a, b, c; while (cin >> a >> b >> c) w[a][b] = c; // 邊ab的權重是c }

最短路徑長度正無限大、負無限大

當起點無法到達終點，就沒有最短路徑了。這種情況常被解讀成：起點永遠走不到終點，導致最短路徑長度正無限大。

當起點到終點之間存在負邊、負環，不斷折返負邊、不斷繞行負環，導致最短路徑的長度負無限大。

「負邊negative edge」是權重為負值的邊。「負環negative cycle」是權重為負值的環。

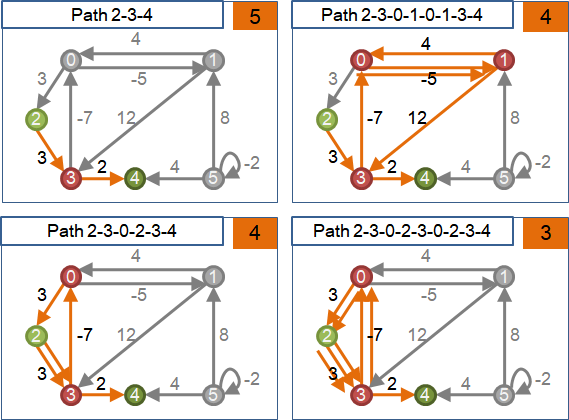
relaxation

最後介紹最短路徑演算法一個共通的重要概念「鬆弛」。

尋找兩點之間的最短路徑時，最直觀的方式莫過於：先找一條路徑，然後再找其他路徑，看看會不會更短，並記住最短的一條。

找更短的路徑並不困難。我們可以尋覓捷徑，以縮短路徑；也可以另闢蹊徑，取代原本的路徑。如此找下去，必會找到最短路徑。

尋覓捷徑、另闢蹊徑的過程，可以以數學方式來描述：現在要找尋起點為s、終點為t的最短路徑，而且現在已經有一條由s到t的路徑，這條路徑上會依序經過a及b這兩點（可以是起點和終點）。我們可以找到一條新的捷徑，起點是a、終點是b的捷徑，以這條捷徑取代原本由a到b的這一小段路徑，讓路徑變短。

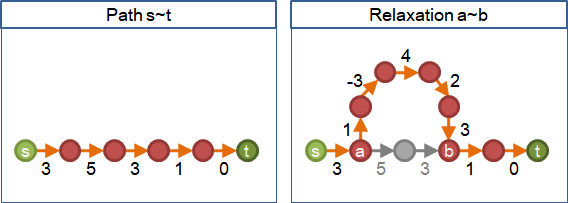
找到捷徑以縮短原本路徑，便是relaxation。

最短路徑演算法的功能類型

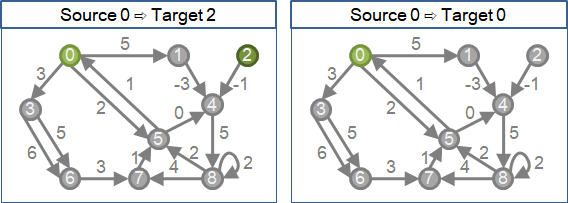
point-to-point shortest path，點到點最短路徑：
給定起點、終點，求出起點到終點的最短路徑。一對一。

single source shortest paths，單源最短路徑：
給定起點，求出起點到圖上每一點的最短路徑。一對全。

all pairs shortest paths，全點對最短路徑：
求出圖上所有兩點之間的最短路徑。全對全。

最短路徑演算法的原理

label correcting：
設定某個點的最短路徑長度之後，之後仍可繼續修正，越修越美。
整個過程就是不斷重新標記每個點的最短路徑長度。

label setting：
逐步設定每個點的最短路徑長度，一旦設定後就不再更改。
只適用於圖上只有正邊和零邊。

用途

一張有向圖，選定一個起點，找出起點到圖上各點的最短路徑，即是找出其中一棵最短路徑樹。

可以順便偵測起點是否會到達負環，然後找出其中一個負環。

演算法

每一條最短路徑，都是邊數更少的最短路徑的延伸。於是乎，建立最短路徑樹，可以從邊數最少的最短路徑開始建立，然後逐步延伸拓展。

由起點開始，不斷朝鄰點拓展，不斷修正鄰點的最短路徑長度，其中必然涵蓋到最短路徑樹的點與邊。拓展過程當中，儘管無法確定最短路徑樹的長相，但是可以確定最短路徑樹正在一點一條生長。

一條最短路徑頂多V-1條邊，一棵最短路徑樹頂多V層。拓展鄰點V-1層之後，必能完成最短路徑樹。

時間複雜度

每一層最多有V個點、E條邊，最多拓展V-1層（遭遇負環則是V層）

圖的資料結構為adjacency matrix是O(V³)；圖的資料結構為adjacency lists是O((V+E)V) = O(V² + VE)，通常簡單寫成O(VE)。

演算法：找出一棵最短路徑樹

令w[a][b]是a點到b點的距離（即是邊的權重）。
令d[a]是起點到a點的最短路徑長度，起點設為零，其他點都設為無限大。

一、起點塞入queue。
二、重複下面這件事，直到queue沒有東西為止：
　甲、queue彈出一點，作為a點。
　　　加速：如果queue已有parent[a]，則捨棄a點，並且重新彈出一點。
　乙、找到一條邊ab：d[a] + w[a][b] < d[b]。
　丙、以邊ab來修正起點到b點的最短路徑：d[b] = d[a] + w[a][b]。
　丁、b點塞入queue。
　　　加速：如果queue已有b點，則不塞入。

int w[9][9]; // adjacency matrix int d[9]; // 記錄起點到各個點的最短路徑長度 int parent[9]; // 記錄各個點在最短路徑樹上的父親是誰 bool inqueue[9];// 記錄queue當中有哪些點 void label_correcting(int source) { for (int i=0; i<9; i++) d[i] = 1e9; d[source] = 0; // 設定起點的最短路徑長度 parent[source] = source; // 設定起點是樹根（父親為自己） queue<int> Q; // queue Q.push(source); // 起點塞入queue // inqueue[source] = true; while (!Q.empty()) { // queue彈出一點，作為a點 int a = Q.front(); Q.pop(); inqueue[a] = false; // 加速：如果queue已有parent[a]，則捨棄a點，並且重新彈出一點。 if (inqueue[parent[a]]) continue; for (int b=0; b<9; ++b) if (w[a][b] != 1e9 && d[a] + w[a][b] < d[b]) { d[b] = d[a] + w[a][b]; // 修正起點到b點的最短路徑長度 parent[b] = a; // b點是由a點延伸過去的 if (!inqueue[b]) { Q.push(b); // b點塞入queue inqueue[b] = true; } } } }

parent[]用來找出最短路徑。

void find_path(int x) // 印出由起點到x點的最短路徑 { if (x != parent[x]) // 先把之前的路徑都印出來 find_path(parent[x]); cout << x << endl; // 再把現在的位置印出來 }

演算法：偵測起點是否會到達負環

最短路徑一旦經過負環，就會不斷地繞行負環，最短路徑長度成為無限短。

如果沒有經過負環，一條最短路徑最多只有V-1條邊；如果經過負環，一條最短路徑就有無限多條邊。順手記錄最短路徑的邊數，就能順手偵測負環。

int w[9][9]; int d[9]; int parent[9]; int n[9]; // 記錄最短路徑的邊數 bool inqueue[9]; void label_correcting(int source) { for (int i=0; i<9; i++) d[i] = 1e9; d[source] = 0; parent[source] = source; n[source] = 0; // 起點到起點的最短路徑的邊數為零 queue<int> Q; Q.push(source); // inqueue[source] = true; while (!Q.empty()) { int a = Q.front(); Q.pop(); inqueue[a] = false; if (inqueue[parent[a]]) continue; for (int b=0; b<9; ++b) if (w[a][b] != 1e9 && d[a] + w[a][b] < d[b]) { d[b] = d[a] + w[a][b]; parent[b] = a; n[b] = n[a] + 1; // 最短路徑的邊數加一 if (n[b] >= 9) return; // 偵測到負環！ if (!inqueue[b]) { Q.push(b); inqueue[b] = true; } } } }

演算法：找出起點可以到達的一個負環

確認負環存在之後，利用parent[]陣列，往回追溯，最短路徑的其中一段一定有著負環。

void label_correcting(int source) { ...... if (n[b] >= 9) { find_negative_cycle(b); return; } ...... } bool visit[9]; void find_negative_cycle(int x) { memset(visit, false, sizeof(visit)); // 往回追溯，直到繞行負環一圈。 for (; !visit[x]; x = parent[x]) visit[x] = true; // 再度繞行負環一圈 cout << "負環上有點" << x; for (int a = parent[x]; a != x; a = parent[a]) cout << "負環上有點" << a; }

演算法：偵測負環

額外增加一個超級起點，連向圖上每一個點，以便抵達圖上各處。如此就能偵測整張圖上是否有負環、從圖上找到一個負環。

UVa 10557 10682

備註

Moore討論兩種情況。單一權重：朝鄰點拓展，不必重複。後人稱作breadth-first search。非負權重：朝鄰點拓展，必須重複。負權重：沒有討論，但是方才的演算法其實可以處理負權重。

那個時代的學者沒有探討資料結構。古時候沒有這些玩意。

後來Pape認為資料結構可以使用deque，依序排隊，視情況插隊。本文內容參考了Pape的版本。

演算法

parallel label correcting algorithm，平行化版本。

圖上所有點同時（或依序）修正鄰點的最短路徑長度，重覆V-1次。如此一來就省去了queue、變成了dynamic programming。

Bellman是dynamic programming創始人。

時間複雜度

時間複雜度等同於label correcting algorithm，但是計算時間較長。現行的時間複雜度標記方式，無法區分兩者的快慢差異。

演算法：找出一棵最短路徑樹

令w[a][b]是a點到b點的距離（即是邊的權重）。
令d[a]是起點到a點的最短路徑長度，起點設為零，其他點都設為無限大。

一、重複下面這件事V-1次：
　甲、窮舉邊ab：d[a] + w[a][b] < d[b]。
　乙、以邊ab來修正起點到b點的最短路徑：d[b] = d[a] + w[a][b]。
　　　（即是圖上所有邊同時進行relaxation。）

int w[9][9]; // adjacency matrix int d[9]; // 記錄起點到各個點的最短路徑長度 int parent[9]; // 記錄各個點在最短路徑樹上的父親是誰 void bellman_ford(int source) { for (int i=0; i<9; i++) d[i] = 1e9; d[source] = 0; // 設定起點的最短路徑長度 parent[source] = source; // 設定起點是樹根（父親為自己） for (int i=0; i<9-1; i++) // 重覆步驟V-1次 for (int a=0; a<9; ++a) // 全部的邊都當作捷徑 for (int b=0; b<9; ++b) if (d[a] != 1e9 && w[a][b] != 1e9) if (d[a] + w[a][b] < d[b]) { d[b] = d[a] + w[a][b]; parent[b] = a; } }

演算法：偵測起點是否會到達負環

拓展鄰點V-1層之後，理論上已經找到最短路徑樹了。若還能再修正最短路徑長度，則必有負環。

bool negative_cycle() { for (int a=0; a<9; ++a) for (int b=0; b<9; ++b) if (d[a] != 1e9 && w[a][b] != 1e9) if (d[a] + w[a][b] < d[b]) return true; return false; }

UVa 558

演算法

randomized label correcting algorithm，隨機化版本。

不斷隨機嘗試圖上每一條邊，逐步修正最短路徑長度。一條一條的邊總有一天將會連接成一條完整的最短路徑、組合成一棵完整的最短路徑樹。

時間複雜度

亂槍打鳥，曠日廢時，最差時間複雜度O(V!)。不過我不會估計平均時間複雜度。

演算法：找出一棵最短路徑樹

令w[a][b]是a點到b點的距離（即是邊的權重）。
令d[a]是起點到a點的最短路徑長度，起點設為零，其他點都設為無限大。

一、重複下面這件事：
　甲、找到一條邊ab：d[a] + w[a][b] < d[b]。
　乙、以邊ab來修正起點到b點的最短路徑：d[b] = d[a] + w[a][b]。

int w[9][9]; // adjacency matrix int d[9]; // 記錄起點到各個點的最短路徑長度 int parent[9]; // 記錄各個點在最短路徑樹上的父親是誰 void ford_algorithm(int source) { for (int i=0; i<9; i++) d[i] = 1e9; d[source] = 0; // 設定起點的最短路徑長度 parent[source] = source; // 設定起點是樹根（父親為自己） while (還能找到一條邊ab：讓d[a] + w[a][b] < d[b]) { d[b] = d[a] + w[a][b]; // 修正由起點到b點的最短路徑長度 parent[b] = a; // b點是由a點延伸過去的 } }

演算法

有向無環圖（directed acyclic graph）只朝一個方向前進，得以依照拓樸順序實施relaxation。

此問題類似「activity network」，演算法是topological sort與dynamic programming。

時間複雜度

兩次graph traversal的時間。圖的資料結構為adjacency matrix是O(V²)；圖的資料結構為adjacency lists是O(V+E)。

演算法：找出一棵最短路徑樹

bool w[9][9]; // adjacency matrix int d[9]; // 記錄起點到各個點的最短路徑長度 int parent[9]; // 記錄各個點在最短路徑樹上的父親是誰 int topo[9]; // 拓樸順序 void shortest_path_tree(int source) { for (int i=0; i<9; i++) d[i] = 1e9; // 拓樸排序，找到其中一個拓樸順序。 topological_ordering(); // 找出起點是在拓撲順序之中的哪一個位置 int p = 0; while (p < 9 && topo[p] != source) p++; // 計算最短路徑長度 d[p] = 0; // 設定起點的最短路徑長度 parent[p] = p; // 設定起點是樹根（父親為自己） for (int i=p; i<9; ++i) // 看看每一個點連向哪些點 for (int j=i+1; j<9; ++j) { int a = topo[i], b = topo[j]; if (d[a] != 1e9 && w[a][b] != 1e9) if (d[a] + w[a][b] < d[b]) { d[b] = d[a] + w[a][b]; parent[b] = a; } } }

另一種寫法。

for (int j=p+1; j<9; ++j) // 看看每一個點被哪些點連向 for (int i=0; i<j; ++i) { int a = topo[i], b = topo[j]; if (d[a] != 1e9 && w[a][b] != 1e9) if (d[a] + w[a][b] < d[b]) { d[b] = d[a] + w[a][b]; parent[b] = a; } }

UVa 10000 10166 10350 10917 1083 ICPC 4449

有向圖可以拆解成一群自環與兩個DAG

索引值一樣、索引值從小往大D+、索引值從大往小D-。自由調整索引值，得到不同的拆法。

演算法

檢查自環是否為負環。若是，演算法結束；若否，自環不影響最短路徑，捨棄之。

每回合先算D+、再算D-，依照拓樸順序實施relaxation，總共V/2回合。時間複雜度O(V/2 ⋅ 2(V+E)) = O(VE)。

一條最短路徑，長度最多V-1。最佳情況是清一色D+或D-，僅一回合。最差情況是D+和D-交錯出現，需要V/2回合。

隨機重排索引值、隨機重製D+和D-，可以避免最差情況，平均V/3回合。但是我不會證明，請見：

《Randomized Speedup of the Bellman–Ford Algorithm》