專著
《Coding Theory: Algorithms, Architectures and Applications》
linear cyclic code引入finite field
請見本站文件「finite field」。
基本單元從GF(2)改成GF(2ʳ)。基本單元從1 bit改成r bits。
數學性質:有限體元素
一個有限體元素(GF(2ʳ))=一段二元碼(長度r)。
GF(2³)
element | binary
————————+———————
α₀ | 000
α₁ | 001
α₂ | 010
α₃ | 011
α₄ | 100
α₅ | 101
α₆ | 110
α₇ | 111
數學性質:有限體加法
有限體的本質是餘數多項式的餘數系統。
係數的模數是任意質數。指定一個質數(此處必須是2),以便進行有限體加法運算。
【註:高位數可以自由設定成左端或右端。此處是左端。】
GF(2³)
element | polynomial | binary
————————+————————————+———————
α₀ | 0 | 000
α₁ | 1 | 001
α₂ | x | 010
α₃ | x + 1 | 011
α₄ | x² | 100
α₅ | x² + 1 | 101
α₆ | x² + x | 110
α₇ | x² + x + 1 | 111
α₁ + α₅
≡ (1) + (x² + 1)
≡ x² + 2
≡ x² remember (mod 2)
≡ α₄
數學性質:有限體乘法
有限體的本質是餘數多項式的餘數系統。
整體的模式是任意質式(r次方)。指定一個質式(r次方),以便進行有限體乘法運算。
GF(2³), irreducible polynomial is x³ + x + 1 (mod 2)
.
element | polynomial | binary
————————+————————————+———————
α₀ | 0 | 000
α₁ | 1 | 001
α₂ | x | 010
α₃ | x + 1 | 011
α₄ | x² | 100
α₅ | x² + 1 | 101
α₆ | x² + x | 110
α₇ | x² + x + 1 | 111
α₂ × α₆
≡ (x) × (x² + x)
≡ x³ + x²
≡ x² + x + 1 remember (mod x³ + x + 1) and (mod 2)
≡ α₇
數學性質:利用生成元,構造有限體元素。
構造有限體元素,可以利用生成元。生成元的各種次方,得到每個有限體元素(除了0)。有限體乘法變得簡單。
GF(2³), irreducible polynomial is x³ + x + 1 (mod 2)
.
generator is x + 1 (mod 2)
.
element | polynomial | binary
————————+———————————————————————+———————
g¹ | (x + 1)¹ ≡ x + 1 | 011
g² | (x + 1)² ≡ x² + 1 | 101
g³ | (x + 1)³ ≡ x² | 100
g⁴ | (x + 1)⁴ ≡ x² + x + 1 | 111
g⁵ | (x + 1)⁵ ≡ x | 010
g⁶ | (x + 1)⁶ ≡ x² + x | 110
g⁷ ≡ g⁰ | (x + 1)⁷ ≡ 1 | 001
數學性質:利用生成元x (mod 2),構造有限體元素。
整體的模式是任意質式(r次方)。質式可以是原多項式,使得x (mod 2)是生成元。有限體乘法變得更簡單。
GF(2³), irreducible polynomial is x³ + x + 1 (mod 2)
.
(primitive polynomial)
generator is x (mod 2)
.
element | polynomial | binary
————————+—————————————————+———————
g¹ | x¹ ≡ x | 010
g² | x² ≡ x² | 100
g³ | x³ ≡ x + 1 | 011
g⁴ | x⁴ ≡ x² + x | 110
g⁵ | x⁵ ≡ x² + x + 1 | 111
g⁶ | x⁶ ≡ x² + 1 | 101
g⁷ ≡ g⁰ | x⁷ ≡ 1 | 001
數學性質:x^(2ʳ-1) - 1質因式分解
xᴺ - 1任選一個因式當作g(x),都能形成線性循環碼。
有限體恰巧有一道數學公式:x^(2ʳ-1) - 1質因式分解。
x^2ʳ - x ≡ (x-0)(x-α₁)(x-α₂)...(x-α2ʳ-1)
x^(2ʳ-1) - 1 ≡ (x-α₁)(x-α₂)...(x-α2ʳ-1)
where GF(2ʳ) = { 0, α₁, α₂, ..., α2ʳ-1 }
每一個有限體元素恰好都出現一次(除了0)。
大家令N = 2ʳ-1。隨便抓幾個因式,都能當作g(x)。爽!
g(x) = (x-α₁)(x-α₃)(x-α₆)...
數學性質:x^(2ʳ-1) - 1質因式分解
事先找到生成元g,數學公式改寫如下。
x^2ʳ - x ≡ (x-0)(x-g¹)(x-g²)...(x-g^(2ʳ-1))
x^(2ʳ-1) - 1 ≡ (x-g¹)(x-g²)...(x-g^(2ʳ-1))
where GF(2ʳ) = { 0, g¹, g², ..., g^(2ʳ-1) }
生成元g、多項式g(x),兩者代表不同事物。生成元x (mod 2)、多項式變數x,兩者代表不同事物。數學符號恰好一樣而已。
g(x) = (x-g⁰)(x-g³)(x-g⁴)...
數學性質:generator matrix
如舊。g(x)每增一項,w(x)則減一項。
碼有2ʳ-1個元素。parity每追加2個元素(2r個位元),資料則減少2個元素(2r個位元)。
⎡g₀ ⎤ ⎡c₀⎤
⎢g₁ g₀ ⎥ ⎡w₀⎤ ⎢c₁⎥
⎢g₂ g₁ g₀ ⎥ ⎢w₁⎥ ⎢c₂⎥
⎢ g₂ g₁ g₀ ⎥ ⎢w₂⎥ = ⎢c₃⎥ G的空白欄位是0
⎢ g₂ g₁ g₀⎥ ⎢w₃⎥ ⎢c₄⎥ g(x) = g₀ + g₁x + g₂x²
⎢ g₂ g₁⎥ ⎣w₄⎦ ⎢c₅⎥
⎣ g₂⎦ ⎣c₆⎦
G w = c
實際範例。
g(x) = (x - g¹)(x - g²)
= x² - (g¹ + g²)x + g³
= g⁰x² + g⁴x + g³
dataword: 0,g⁰,g²,g³,0 隨便設定
codeword: 0,g³,g⁰,g⁰,g⁶,g³,0 手工計算,可能算錯
⎡g³ ⎤ ⎡0 ⎤
⎢g⁴ g³ ⎥ ⎡0 ⎤ ⎢g³⎥
⎢g⁰ g⁴ g³ ⎥ ⎢g⁰⎥ ⎢g⁰⎥
⎢ g⁰ g⁴ g³ ⎥ ⎢g²⎥ = ⎢g⁰⎥ G的空白欄位是0
⎢ g⁰ g⁴ g³⎥ ⎢g³⎥ ⎢g⁶⎥
⎢ g⁰ g³⎥ ⎣0 ⎦ ⎢g³⎥
⎣ g⁰⎦ ⎣0 ⎦
G w = c
g(x) = (x - g¹)(x - g²)
= x² - (g¹ + g²)x + g³
= g⁰x² + g⁴x + g³
= 001
x² + 110
x + 011
dataword: 000,001,100,011,000 請自行去掉逗點
codeword: 000,011,001,001,101,011,000
⎡011 ⎤ ⎡000⎤
⎢110 011 ⎥ ⎡000⎤ ⎢011⎥
⎢001 110 011 ⎥ ⎢001⎥ ⎢001⎥
⎢ 001 110 011 ⎥ ⎢100⎥ = ⎢001⎥ G的空白欄位是000
⎢ 001 110 011⎥ ⎢011⎥ ⎢101⎥
⎢ 001 110⎥ ⎣000⎦ ⎢011⎥
⎣ 001⎦ ⎣000⎦
G w = c
順帶一提,乘上x,不再是移位一個位元了,而是移位r個位元。「循環移位」的概念不太一樣了。
數學性質:parity-check matrix
如舊。
⎡c₀⎤
⎢c₁⎥
⎡h₅ h₄ h₃ h₂ h₁ h₀ ⎤ ⎢c₂⎥ ⎡0⎤
⎣ h₅ h₄ h₃ h₂ h₁ h₀⎦ ⎢c₃⎥ = ⎣0⎦ H的空白欄位是0
⎢c₄⎥
⎢c₅⎥
⎣c₆⎦
H c = 0
實際範例就不給了。總之差不多。
數學性質:annihilator matrix
【尚無正式名稱。目前大家稱作parity-check matrix。】
g(x)只有一次方質因式,恰好擁有特殊數學性質。
首先簡單一點,令g(x) = (x-α)。
碼變成多項式c(x)。所有碼都是(x-α)的倍數。所有碼都有因式(x-α)。所有碼都有根α。所有碼滿足c(α) = 0。c(α) = c₀α⁰ + c₁α¹ + c₂α² + ... = 0。改寫成矩陣乘法,矩陣只有一個橫條。
⎡c₀⎤
⎢c₁⎥
⎢c₂⎥
[α⁰ α¹ α² α³ α⁴ α⁵ α⁶] ⎢c₃⎥ = [0]
⎢c₄⎥
⎢c₅⎥
⎣c₆⎦
A c = 0
令g(x) = (x-α₁)(x-α₂)...。
所有碼滿足c(α₁) = 0且c(α₂) = 0且...。追加橫條即可。
⎡c₀⎤
⎢c₁⎥
⎡α₁⁰ α₁¹ α₁² α₁³ α₁⁴ α₁⁵ α₁⁶⎤ ⎢c₂⎥ ⎡0⎤
⎢α₂⁰ α₂¹ α₂² α₂³ α₂⁴ α₂⁵ α₂⁶⎥ ⎢c₃⎥ = ⎢0⎥
⎣ : : : : : : : ⎦ ⎢c₄⎥ ⎣:⎦
⎢c₅⎥
⎣c₆⎦
A c = 0
annihilator matrix與parity-check matrix完全等價,高斯消去法結果一致。【尚待確認】
Reed–Solomon code
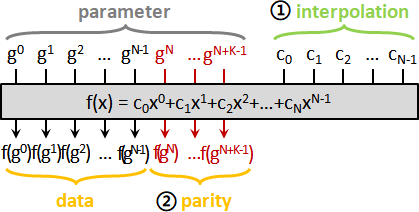
生成多項式g(x),設定t個根:生成元α = g的連續次方。
g(x) = (x-α⁰)(x-α¹)(x-α²)...(x-αᵗ⁻¹)
大家習慣從0次方開始。其實也可以從任意次方值開始。
g(x) = (x-αⁱ)(x-αⁱ⁺¹)...(x-αⁱ⁺ᴷ⁻¹)
α是生成元,確保每一種次方都是相異元素。
採用連續次方,原因是容易設計演算法、電路。
編碼
資料w(x),碼c(x) = w(x)g(x)。
乘上g(x)可以想成是追加parity。
所有的碼
窮舉w(x),那麼c(x) = w(x)g(x)即是所有碼。
c(x) = w(x)g(x)代入α⁰ α¹ α² ... αᵗ⁻¹都是零。
碼的兩兩距離
仿照Hamming code,證明碼的兩兩距離皆大於等於t+1。
利用annihilator matrix得到所有碼。annihilator matrix恰是Vandermonde matrix的子矩陣,其determinant有數學公式。
⎡c₀⎤
⎡ (α⁰)⁰ (α⁰)¹ (α⁰)² (α⁰)³ (α⁰)⁴ (α⁰)⁵ (α⁰)⁶ ⎤ ⎢c₁⎥ ⎡0⎤
⎢ (α¹)⁰ (α¹)¹ (α¹)² (α¹)³ (α¹)⁴ (α¹)⁵ (α¹)⁶ ⎥ ⎢c₂⎥ = ⎢0⎥
⎢ (α²)⁰ (α²)¹ (α²)² (α²)³ (α²)⁴ (α²)⁵ (α²)⁶ ⎥ ⎢c₃⎥ ⎢0⎥
⎢ : : ⎥ ⎢c₄⎥ ⎢:⎥
⎣(αᵗ⁻¹)⁰ ... (αᵗ⁻¹)⁶⎦ ⎢c₅⎥ ⎣0⎦
⎣c₆⎦
A c = 0
符號一覽表
r = length of binary presentation of finite field
q = alphabet size = 2^r
n = codeword length = q-1
k = dataword length = message length
t = syndrome number = root number of g(x) = n-k = m
d = minimum codeword distance = t+1
ν = error number ≤ ⌊(d-1)/2⌋ = ⌊t/2⌋
解碼(Peterson–Gorenstein–Zierler decoder)
1. get t symdromes from codeword.
(speedup: Horner's rule O(nt) )
(speedup: multipoint evaluation O(𝓜(n) + 𝓜(t)logt) )
2. get minimal polynomial of t syndromes.
aka error locator polynomial with minimum errors.
(speedup: Berlekamp–Massey algorithm O(tν) )
(speedup: Brent–Gustavson–Yun algorithm O(𝓜(t)logν) )
3. find ν error locators from minimal polynomial Λ(x)
by evaluating Λ(α-0) ... Λ(α-(n-1)) and taking the zeros.
(speedup: Chien search O(νn) )
(speedup: multipoint evaluation O(𝓜(ν) + 𝓜(n)logn) )
4. find ν error magnitudes from ν error locators and t syndromes.
(speedup: Forney algorithm)
5. codeword -= error
實務上n t ν很小,導致每個步驟的第一個演算法優於第二個演算法。雖然時間複雜度較高,但是過程較短,況且可以平行計算。
設計error locator polynomial,展開得到係數:根總和、根兩兩乘積和、根三三乘積和、……。形成Newton's identity。
實作細節請見恩智浦、德州儀器、英國廣播公司的技術報告。
解碼(FFT decoder)
1. get t syndromes by n-point FFT of codeword.
O(nlogn)
2. get minimal polynomial of t symdromes.
O(tν)
3. get remaining (n-t) syndromes from minimal polynomial.
O((n-t)ν)
4. get error by n-point IFFT of n syndromes.
O(nlogn)
5. codeword -= error.
O(n)
各個步驟所使用的運算:正向數論轉換、線性遞迴函數內插、線性遞迴函數求值、逆向數論轉換、多項式減法。演算法請見本站文件「number theoretic transform」「polynomial (recurrence)」。
幹古
Reed–Solomon code學習門檻很高。
舉例來說,知名的最短路徑演算法Dijkstra's algorithm約有三階階梯:圖論元件(點、邊、權重、陣列或串列)、貪心策略(最短路徑末端截去一段還是最短路徑,而且長度更短或相同)、紀錄路徑長度(陣列或堆積)。
相比之下,Reed–Solomon code少說也有十階階梯。
本站收錄上千種演算法,相當變態。其中Reed–Solomon code學習門檻位居第一,簡直變態到不行。因此我決定特地撰文介紹Reed–Solomon code的先備知識,方便大家理解什麼是變態。
Reed–Solomon code的數字系統,不是整數,也不是餘數,而是「有限體」。「有限體運算」可以改寫成「餘數多項式運算」。「餘數多項式運算」是「餘數運算」和「多項式運算」兩者併用。餘數運算源自「整數運算」與「因數」與「質數」。多項式運算源自「數列運算」與「生成函數」。
電腦採用二進位。有限體習慣採用GF(2ⁿ)。「餘數多項式運算」習慣簡化成「位元運算」。
構造有限體元素,使用了「有限體的原多項式」,源自「餘數的原根(單位圓的單位根的次方循環)」,又源自「群的生成元」。
Reed–Solomon code發展自Hamming code和BCH code。Hamming code是一種parity-check code,等價於linear code,需要「線性代數」的知識。BCH code同時是linear code和cyclic code,後者需要「位元」和「多項式」的知識。
Reed–Solomon code原理是「多項式內插」。因此annihilator matrix恰是「內插矩陣Vandermonde matrix」。x值設定成同一個數字的每一種次方,而且x值是有限體。因此annihilator matrix同時也是「傅立葉矩陣Fourier matrix」。
Reed–Solomon code編碼與解碼,包含「多項式的加減乘除、多點求值、最大公因數」、「線性遞迴函數的求值、內插」、「數列的數論轉換」。順帶一提,這些運算可以表示成「多項式形式」或「矩陣形式」,而教科書習慣採用「矩陣形式」。
我講完了。來個結語。雖然Reed–Solomon code少說也有十階階梯,但是現實世界的事物更加複雜。比方來說,機車零件約一百種、汽車零件約一千種,維修製造車輛可是複雜多了。便利商店貨品品項至少一千種、大賣場至少一萬種,貨品進銷存可是複雜多了。十階階梯在現實世界只是小玩意兒,無非是熟不熟悉而已,不必自己嚇自己。所謂變態,其實只不過是這麼一回事。
編碼率
每追加2個元素(2r個位元),只能額外修正1個元素(r個位元)。
應用
雖然Reed–Solomon code已經不敵後起之秀,諸如LDPC code和turbo code,但是現今仍然可以見到實際應用,主要都是古代流傳至今的重要發明:光碟CD/DVD/BD、條碼QR code、電話線上網ADSL/VDSL。