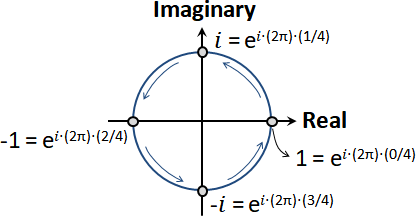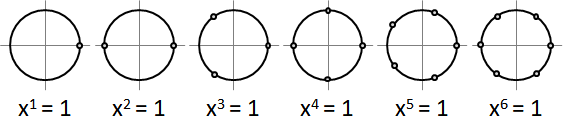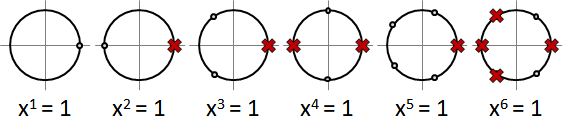楔子
雖然本章標題是有限體多項式,但是為了把事情講清楚,本章將介紹各種多項式,其中包含有限體多項式。
polynomial
實數多項式(real polynomial):係數是實數。標記成ℝ[X]。
複數多項式(complex polynomial):係數是複數。標記成ℂ[X]。
整數多項式(integer polynomial):係數是整數。標記成ℤ[X]。
餘數多項式(residue polynomial):係數是餘數。標記成(ℤ/mℤ)[X]或ℤₘ[X]。
有限體多項式(finite field polynomial):係數是有限體。標記成GF(pⁿ)[X]或𝔽pⁿ[X]。
餘數多項式、模數是質數p:可以視作有限體多項式的特例。標記成GF(p)[X]或𝔽ₚ[X]。
GF(p)擴張體(extension field of GF(p)):把GF(p)[X]弄成有限體。等價於GF(pⁿ)。
polynomial心照不宣的慣例
係數與變數不見得是相同類型。
經典範例:係數是實數、變數是複數(實數多項式的共軛複數根)。
每當數學家討論多項式,係數是已知類型,變數是未知類型!我們不能私自推定變數擁有特殊性質,除非明確指定了變數類型。
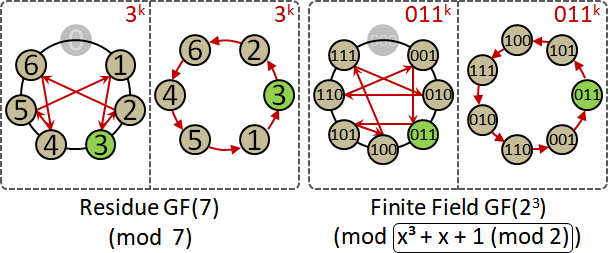
經典範例:餘數多項式,係數是餘數(模數為p),變數是未知類型。變數不可以次方循環(x^p ≡ x不成立)。
irreducible polynomial(prime polynomial)
「不可約多項式」。俗稱「質式」。無法用乘法分解的多項式。
係數是已知類型、變數是未知類型,則存在質式。
因式的次方值,必定遞減,直到收斂。
x² + 1 (mod 5)
≡ x + 2 (mod 5)
× x + 3 (mod 5)
x² + 1 (mod 5)
is not an irreducible polynomial
x + 2 (mod 5)
and x + 3 (mod 5)
are irreducible polynomials
係數與變數都是已知類型,則不一定存在質式。
因式的次方值,可能變大,無法收斂。
經典範例:係數與變數都是餘數。
x² + 1 (mod 5)
≡ x³ + 2 (mod 5)
× x³ + 3 (mod 5)
irreducible polynomial心照不宣的慣例
每當數學家討論質式,習慣把變數重新視作未知類型!即便變數是已知類型!
monic polynomial
「首一多項式」。最高次方項(首項)係數是一的多項式。
實數的乘法分解有無限多種方式,導致實數多項式的倍率提取有無限多種方式。
餘數多項式、有限體多項式亦然。
x + 2 (mod 5)
≡ 2 (mod 5)
× 3x + 1 (mod 5)
≡ 3 (mod 5)
× 2x + 4 (mod 5)
≡ 4 (mod 5)
× 4x + 3 (mod 5)
實數多項式的因式分解,可以提取適當倍率,讓所有因式的首項係數均是1。
餘數多項式、有限體多項式亦然。
2x² + 2x + 1 (mod 5)
≡ 2 (mod 5)
× x² + x + 3 (mod 5)
≡ 2 (mod 5)
× x + 2 (mod 5)
× x + 4 (mod 5)
當模數是質數,那麼餘數多項式恰有唯一一種因式分解方式!
monic polynomial心照不宣的慣例
每當數學家討論整數多項式,因式與質式不是首一多項式。
每當數學家討論實數多項式、餘數多項式、有限體多項式,因式與質式預設是首一多項式。
minimal polynomial
「最小多項式」。包含指定的根r(甚至指定許多根r₁ r₂ ...),而且度數盡量小(因式盡量少),而且首項係數是1。
根與係數通常是不同類型!變數仍是未知類型!
如果根與係數是相同類型,最小多項式是(x-r₁)(x-r₂)...。缺乏討論意義。
如果根與係數是不同類型,最小多項式是(x-r₁)(x-r₂)...,再乘上其他因式,使得根類型恰巧轉變成係數類型。
經典範例:係數是實數、根是複數。想要包含指定的複數根r,需要因式(x-r),還需要追加因式(x-r̅),其中r̅是r的共軛複數。兩者相乘才能湊得實數多項式。
(根與係數是已知類型)最小多項式⊂(根類型只能是係數類型)質式。數學家習慣省略前綴:最小多項式⊂質式。
minimal polynomial心照不宣的慣例
每當數學家討論最小多項式,根與係數是不同類型!
cyclotomic polynomial
「分圓多項式」。最小多項式,係數是整數,根是複數,指定的根是單位根。
數學家已經找到公式解。一步一步來:
單位圓:複數平面上,圓心為原點、半徑為1。
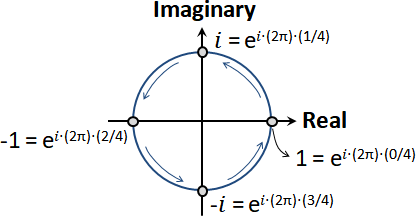
n次單位根:方程式xⁿ = 1的根。單位圓上的n等分點。習慣寫成歐拉公式。
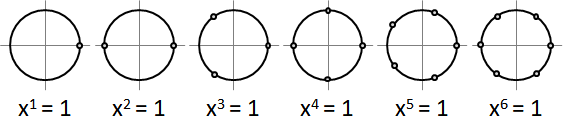
n次單位原根:n次單位根,但不是更低次單位根。無法約分的等分點。跟n互質的等分點。數量顯然是φ(n)個,φ是互質數計數函數。
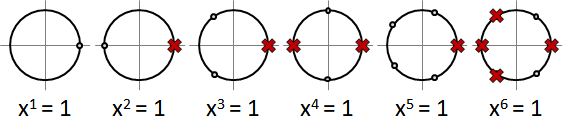
分圓多項式:n次單位原根,作為因式。因式相乘之後,恰為整數多項式,而且因式數量是最少的(形成最小多項式)。證明省略。

分圓多項式公式解:所有的n次單位原根,作為因式。
Φ₁(x) = (x - ω(1/1))
= x - 1
Φ₂(x) = (x - ω(1/2))
= x + 1
Φ₃(x) = (x - ω(1/3))(x - ω(2/3))
= x² + x + 1
Φ₄(x) = (x - ω(1/4))(x - ω(3/4))
= x² + 1
Φ₅(x) = (x - ω(1/5))(x - ω(2/5))(x - ω(3/5))(x - ω(4/5))
= x⁴ + x³ + x² + x + 1
Φ₆(x) = (x - ω(1/6))(x - ω(5/6))
= x² - x + 1
: :
where ω(t) = e𝑖⋅2π⋅t
primitive polynomial
「原多項式」。最小多項式,係數是有限體GF(p),根是有限體GF(pⁿ),指定的根是原元素。
原多項式宛如分圓多項式,但是細節稍微不同。數學家已經找到公式解。一步一步來:
GF(pⁿ)費馬小定理:x^(pⁿ-1) ≡ 1的解,是全體元素去掉0。
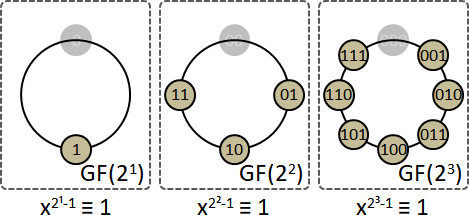
GF(pⁿ)原元素:g¹ g² ... 都不是1,直到g^(pⁿ-1)才是1。換句話說,x^(pⁿ-1) ≡ 1的解,但不是更低次的解。數量顯然是φ(pⁿ-1)個,φ是互質數計數函數。證明省略。
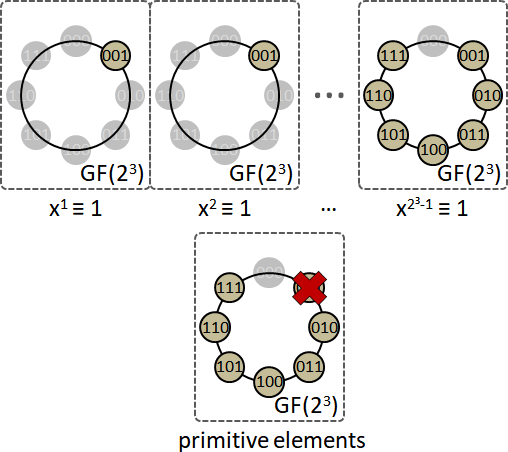
原多項式:GF(pⁿ)原元素,各種p次方的次方,作為因式。因式相乘之後,恰為GF(p)多項式,而且因式數量是最少的(形成最小多項式)。證明省略。
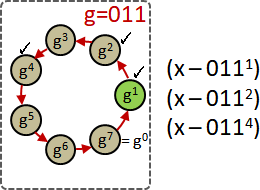
原多項式公式解:g是任意一個GF(pⁿ)原元素。
F(x) = (x - g)(x - g^p¹)(x - g^p²)...(x - g^pⁿ⁻¹)
primitive polynomial特殊功用
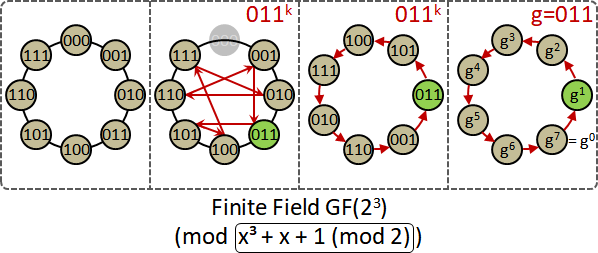
構造有限體,需要指定模數,模數是質數暨質式。將模數設定成原多項式,那麼x一定是原元素(生成元)。證明省略。
x是原元素,計算過程變得非常簡單!
GF(2³), irreducible polynomial is
primitive polynomial x³ + x + 1 (mod 2)
.
therefore x (mod 2)
must be a primitive element.
x¹ ≡ x ---> 010₍₂₎
x² ≡ x² ---> 100₍₂₎
x³ ≡ x + 1 ---> 011₍₂₎
x⁴ ≡ x² + x ---> 110₍₂₎
x⁵ ≡ x² + x + 1 ---> 111₍₂₎
x⁶ ≡ x² + 1 ---> 101₍₂₎
x⁷ ≡ 1 ---> 001₍₂₎
質式、原元素,目前都沒有快速的演算法,所幸網路上已經有現成的表格了。原多項式,演算法是高斯消去法。既然如此,選擇原多項式,事情比較簡單。
這個特殊功用,就是本章唯一重點。前面鋪陳一長串數學術語,就是為了介紹這個特殊功用。數學家這份工作,就是這麼辛苦。
總結
不可約多項式(irreducible polynomial):無法因式分解。地位宛如質數。乾脆叫做質式。
首一多項式(monic polynomial):首項係數為一。
最小多項式(minimal polynomial):次方值最低、首項係數為1、包含指定的根。可視作質式。
單位根(root of unity):方程式xⁿ = 1的根。複數平面單位圓n等分。每個指數對應每個單位根。
單位原根(primitive root of unity):n次單位根,且不是更低次單位根。顯然指數與n互質。顯然數量是φ(n)個。任意一個n次單位原根,其每個次方恰好生成每個n次單位根。
分圓多項式(cyclotomic polynomial):第n個分圓多項式,根是所有的n次單位原根。恰巧得到整數多項式。可視作最小多項式,可視作質式。
費馬小定理(Fermat's little theorem):等號兩側同除x,得到x^(pⁿ - 1) ≡ 1。GF(pⁿ)每個非零元素宛如pⁿ - 1次單位根。
生成元(generator):特定元素,反覆實施特定運算,生成特定集合。
原根(primitive root):GF(p)生成元,每個次方恰好生成每個非零元素。GF(p)恰有φ(p - 1) = φ(φ(p))個原根。地位宛如p-1次單位原根。
原元素(primitive element):GF(pⁿ)生成元,每個次方恰好生成每個非零元素。GF(pⁿ)恰有φ(pⁿ - 1)個原元素。
原多項式(primitive polynomial):n次原多項式,根是n個相異的GF(pⁿ)原元素,而且必須恰巧得到GF(p)[X]。n次原多項式的數量是φ(pⁿ - 1) / n個。可視作最小多項式,可視作質式。