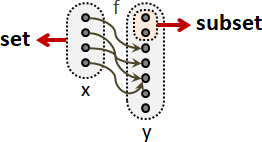
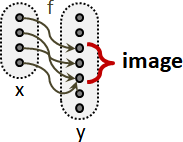
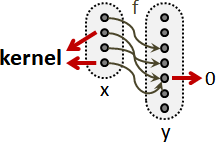
楔子
計算學家重視數值,本站以變數的加減、變數的倍率來介紹「線性函數(狹義版本)」。
數學家重視性質,以函數的加法性、函數的倍率性來定義「線性函數(廣義版本)」。
儘管本站的介紹方式比較直覺,卻是非常偏頗的介紹方式。為了端正視聽,以下簡述數學家的介紹方式。完全是另外一種世界觀。
vector space的由來
變數的加減、變數的倍率,變數可以是各種東西。
f(x) = 2 ⋅ x + 3 ⋅ y + 5 ⋅ z 線性函數(狹義版本)
f(x) = 2 ⋅ 1.414 + 3 ⋅ 3.14 + 5 ⋅ 2.71 變數是實數
f(x) = 2 ⋅ (x²+x) + 3 ⋅ (x²+x+1) + 5 ⋅ (x-1) 變數是多項式
f(x) = 2 ⋅ ↗ + 3 ⋅ ↖ + 5 ⋅ → 變數是施力
f(x) = 2 ⋅ 🍎 + 3 ⋅ 🍓 + 5 ⋅ 🍒 變數是水果
於是數學家創造了「向量空間」這個泛稱!
vector space
「向量空間」由一個集合、兩個運算組成。兩個運算分別是加法運算、倍率運算。
理想名稱應是「加倍空間」。古人將加法、倍率聯想到物理向量,所以才取名「向量空間」。
集合:可以設定成實數、整數、餘數、多項式、向量、函數、……。
加法運算、倍率運算:泛指一切適當的運算。可以設定成實數加法與實數倍率,也可以設定成實數乘法與實數次方。設定方式通常不只一種。
為了釐清加法運算與倍率運算的責任,數學家做了詳細規定:
向量空間之加法運算的規定
1. associativity 加法結合律
u + (v + w) = (u + v) + w
2. commutativity 加法交換律
u + v = v + u
3. identity element 加法單位元素
v + 0 = v
4. inverse element 加法反元素(負數、減法)
v + (-v) = 0
向量空間之倍率運算的規定
5. associativity 倍率結合律
a ⋅ (b ⋅ v) = (a ⋅ b) ⋅ v
6. distributivity of vector sum 倍率分配律,針對向量部分
a ⋅ (u + v) = (a ⋅ u) + (a ⋅ v)
7. distributivity of scalar sum 倍率分配律,針對倍率部分
(a + b) ⋅ v = (a ⋅ v) + (b ⋅ v)
8. identity element 倍率單位元素
1 ⋅ v = v
集合當中所有元素,必須符合所有規定。
符號uvw0:向量空間的集合的元素。符號ab1:倍率。符號01:泛指符合規定的元素,而且至少要有一個、必須存在。
倍率運算的倍率值,通常設定成「體field」。體由一個集合、兩個運算組成。兩個運算分別是加法運算、乘法運算。數學家也做了詳細規定,不過此處省略。
vector space實際範例
集合設定成多項式,加法運算設定成多項式加法,倍率運算設定成多項式倍率。
倍率的集合設定成實數,倍率的加法運算設定成實數加法,倍率的乘法運算設定成實數乘法。
0是零多項式,1是實數1。此例的0和1剛好是單一元素,而且非常直覺;但是當集合設定成其他特殊的集合,0和1就可能有多種元素。
vector space實際範例
再舉一個複雜的例子。
向量空間
集合 --> 餘數 mod n
加法運算 --> 餘數乘法×
倍率運算 --> 餘數次方^
體(倍率運算的倍率值)
集合 --> 整數 (甚至推廣為餘數 mod φ(n))
加法運算 --> 整數加法+ (甚至推廣為餘數加法)
乘法運算 --> 整數乘法× (甚至推廣為餘數乘法)
向量空間之加法運算的規定 let u=2, v=3, w=4, a=5, b=6, n=7
1. u + (v + w) = (u + v) + w | 2 × (3 × 4) ≡ (2 × 3) × 4
2. u + v = v + u | 2 × 3 ≡ 3 × 2
3. v + 0 = v | 3 × 1 ≡ 3 符號0是餘數1
4. v + (-v) = 0 | 3 × 3 ≡ 3 × 5 ≡ 1 倒數
向量空間之倍率運算的規定
5. a ⋅ (b ⋅ v) = (a ⋅ b) ⋅ v | (2 ^ 6) ^ 5 ≡ 2 ^ (5 × 6)
6. a ⋅ (u + v) = a ⋅ u + a ⋅ v | (2 × 3) ^ 5 ≡ (2 ^ 5) × (3 ^ 5)
7. (a + b) ⋅ v = a ⋅ v + b ⋅ v | 3 ^ (5 + 6) ≡ (3 ^ 5) × (3 ^ 6)
8. 1 ⋅ v = v | 3 ^ 1 ≡ 3 符號1是整數1
inner product space
「內積空間」由一個集合、三個運算組成。三個運算分別是加法運算、倍率運算、內積運算。
理想名稱應是「加倍內空間」,不過這名稱有點拗口。
內積運算:泛指一切適當的運算。例如集合設定成向量、加法運算設定成向量加法、倍率運算設定成向量倍率、內積運算設定成向量點積。設定方式通常不只一種。
為了釐清內積運算的責任,數學家做了詳細規定:
內積空間之內積運算的規定
9. additivity 加法分配律
(u + v) ∙ w = (u ∙ w) + (v ∙ w)
10. homogeneity of degree 1 倍率結合律
(a ⋅ u) ∙ w = a ⋅ (u ∙ w)
11. commutativity 內積交換律
u ∙ v = v ∙ u
12. positive definiteness 正定
u ∙ u ≥ 0
u ∙ u = 0 iff u = 0
內積空間是向量空間的延伸版本。數學家之所以發明內積空間,是因為有了內積運算之後,可以引入長度和角度的概念。
「範數norm」泛指一切「自己與自己的內積、再開根號」的情況。如果集合設定成向量,內積運算設定成向量點積,那麼範數是指向量長度。
「正交orthogonality」泛指一切「內積等於零」的情況。如果採用方才的設定,那麼正交是指向量垂直。
抽象化
汽車、貨車、公車、聯結車,泛稱為「車」。由實際名稱變成泛稱的這個過程,叫做「抽象化abstraction」。
數學家非常喜歡抽象化。上述名詞,諸如加法運算、倍率運算、內積運算、向量空間、內積空間、範數、正交,都是泛稱,都是經過抽象化的名稱。
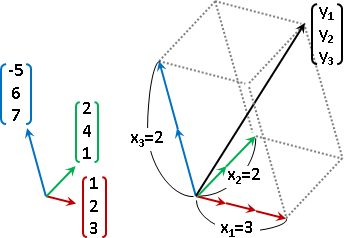
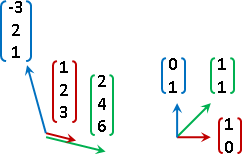
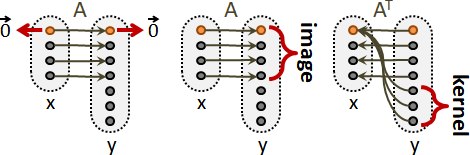
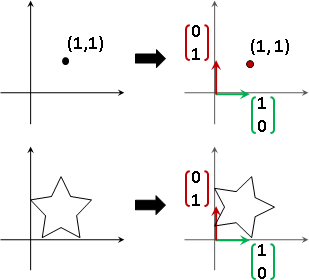
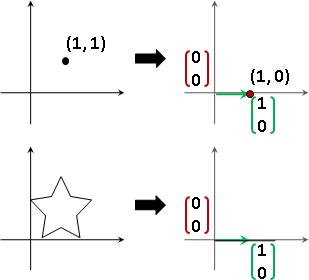
basis / coordinate
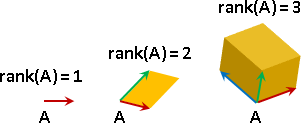
向量空間,從中選定一組元素們,當作座標軸(基底)。座標軸互相「線性獨立linear independent」,座標軸數量(維度)足以生成所有元素。符合條件的座標軸有無限多組。
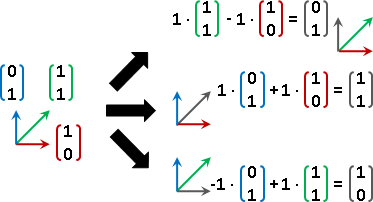
選定座標軸之後,座標軸各自利用倍率運算進行縮放,然後利用加法運算進行合成,就可以得到向量空間當中每一個元素。得到一個元素的過程稱作「線性組合linear combination」,得到每一個元素的過程稱作「生成span」。
反過來說,向量空間的每一個元素,也可以利用分量的概念,分散到每個座標軸上面,得到一個座標,座標其實就是倍率。每一個元素各自擁有獨一無二的座標。
vector space: V
element v of V: v ∈ V
basis of V: {v₁, v₂, ..., vɴ}
linear combination: v = c₁v₁ + c₂v₂ + ... + cɴvɴ
span: V = span(v₁, v₂, ..., vɴ)
coordinate of v: {c₁, c₂, ..., cɴ}
axiom of choice = vector space has basis
符合條件的座標軸,一定存在嗎?數學家訂立公設,聲稱存在。
數學家訂立「選擇公設」,假設向量空間必有一組線性獨立的元素、假設向量空間必有座標軸(基底)、假設向量空間每個元素的線性組合可以有唯一方式。這些事情都等價,此處省略證明。
線性組合有唯一方式(函數的概念),理應是主角,理應命名與定義。然而數學家卻讓主角變旁白,將之塞入向量空間(變數的概念),利用「選擇公設」聲稱它存在。
這部作品的世界觀設定,實在是太複雜了。
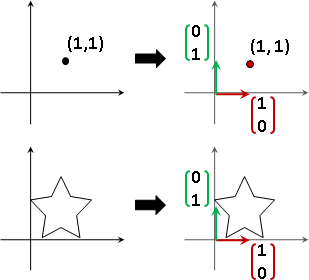
linear function
終於來到正題。狹義版本推廣成廣義版本。加法分配律、倍率結合律推廣成加性函數、倍性函數。
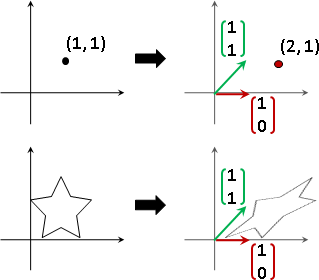
additive function:
additive
y₁ + y₂ = f(x₁) + f(x₂) ======== f(x₁ + x₂)
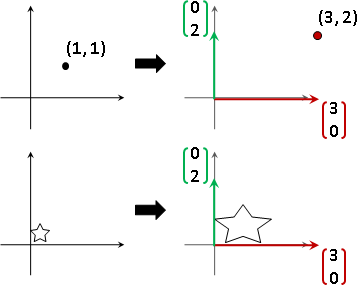
homogeneous function of degree 1:
homogeneous
k ⋅ y = k ⋅ f(x) =========== f(k ⋅ x)
linear function f: affine function g:
1. f(x₁+x₂) = f(x₁) + f(x₂) 1. f(x₁+x₂) = f(x₁) + f(x₂)
2. f(kx) = k f(x) 2. f(kx) = k f(x)
3. g(x) = f(x) + c
加性函數:輸入相加等同輸出相加。先相加再代入,等於先代入再相加。
倍性函數:輸入倍率等同輸出倍率。先乘上倍率再代入,等於先代入再乘上倍率。
線性函數:加性函數暨倍性函數。
仿射函數:線性函數納入常數加法。
線性函數跟直線無關。取名線性是因為古人沒有考慮清楚。理想名稱應是「加倍函數」。
為了迎合定義、為了能夠運算,輸入輸出必須是向量空間,或者是內積空間。理想名稱應是「加倍空間」、「加倍內空間」。
廣義版本的新功能
一、輸入與輸出可以是不同類型的東西。
二、函數可以有加法和倍率以外的運算。
例如微積分的極限運算lim、機率論的期望值運算E[],都是線性函數。
廣義版本的功效
由於加性函數、倍性函數,使得座標軸的線性組合、再實施變換,等同座標軸實施變換、再線性組合。
linear function f: X -> Y
basis(X) = {x₁, x₂, ..., xɴ} coordinate(x) = {c₁, c₂, ..., cɴ}
basis(Y) = {y₁, y₂, ..., yɴ} coordinate(y) = {c₁, c₂, ..., cɴ}
linear combination:
x = c₁x₁ + c₂x₂ + ... + cɴxɴ
linear function:
y = f(x)
y = f(c₁x₁ + c₂x₂ + ... + cɴxɴ)
y = c₁ f(x₁) + c₂ f(x₂) + ... + cɴ f(xɴ)
y = c₁ y₁ + c₂ y₂ + ... + cɴ yɴ
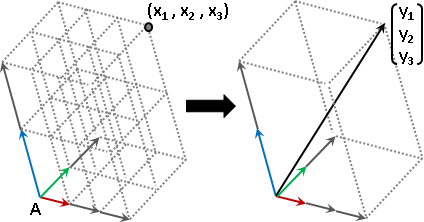
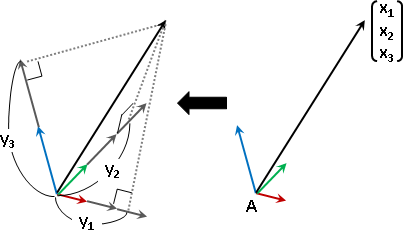
線性函數有什麼功效呢?分別觀察座標軸和座標:
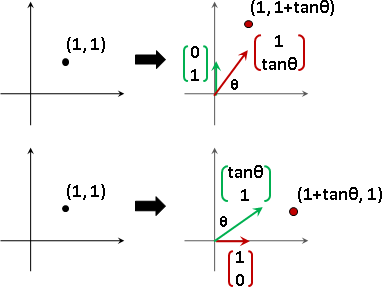
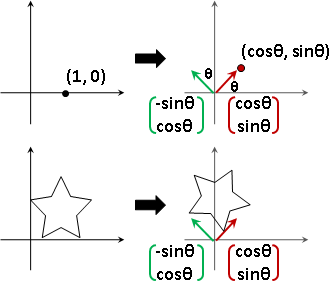
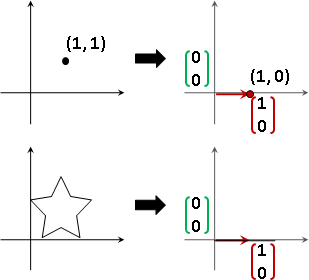
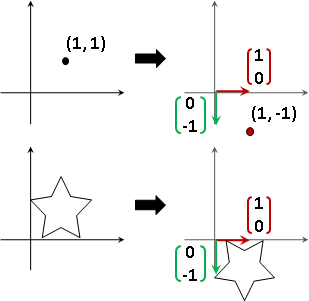
輸入的座標軸,套用函數,實施變換,得到輸出的座標軸!
basis(X) = {x₁, x₂, ..., xɴ}
basis(Y) = {f(x₁), f(x₂), ..., f(xɴ)}
輸入形成座標系統,輸出也形成座標系統。輸入輸出一一對應,座標一一相等!
coordinate(x) = {c₁, c₂, ..., cɴ}
coordinate(y) = {c₁, c₂, ..., cɴ}
廣義版本的特色
一、輸入輸出各自擁有座標軸。輸入的座標軸,套用函數,得到輸出的座標軸。
二、座標軸有無限多種選擇,隨便一種都行。
三、輸入輸出的座標軸通常不同,但是座標一定相同。
四、線性函數是座標不變、座標軸改變。
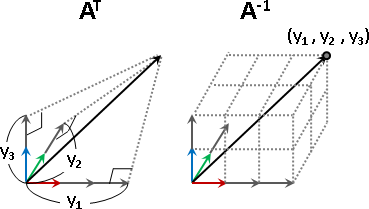
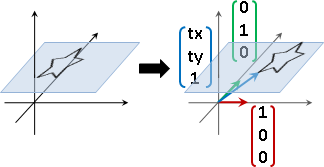
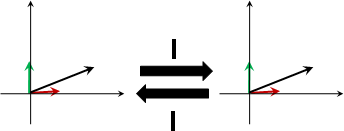
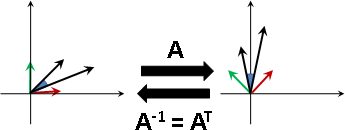
change of basis / similar matrices
輸入的座標軸進行更換。輸出的座標軸也隨之更換。
輸入的座標軸、輸出的座標軸,互為相似矩陣。
本站文件曾經提到:「更換座標系」的其中一種方式是「套用函數組」。當然也可以「套用線性函數」。
然而數學家卻採用了中古奇幻世界觀設定:因為是「線性函數」所以才能「更換座標系」。有興趣的讀者請自行穿越異世界:
在異世界當中,「更換座標系」是初學者最難掌握的線性代數主題之一。如果你既不是主角更沒有外掛,那麼請你自己保重。
linearization(linear approximation)【尚無正式名稱】
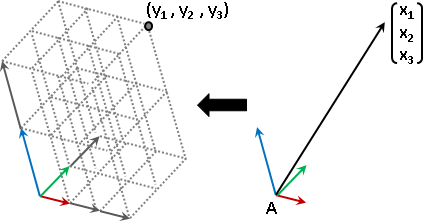
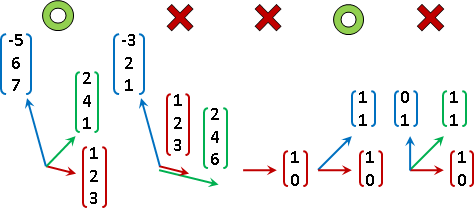
狹義線性函數求值,可以拆成兩個步驟:
一、函數視作座標軸。(線性獨立、維度足夠)
二、輸入元素視作座標,求輸出元素。
廣義線性函數求值,可以拆成四個步驟:
一、選定輸入的座標軸。(線性獨立、維度足夠)
二、求得輸出的座標軸。(輸入的座標軸,一一套用函數)
三、輸入元素,求座標。(根據輸入的座標軸)
四、座標,求輸出元素。(根據輸出的座標軸)
「線性化」。非線性函數硬是改成線性函數。雖然不是線性函數,卻硬是用上述手法計算,求得近似值。
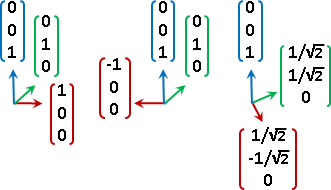
為了方便求得座標,輸入的座標軸習慣選擇正規正交矩陣,以投影公式求得座標:輸入元素與座標軸的內積(不必除以座標軸長度平方)。
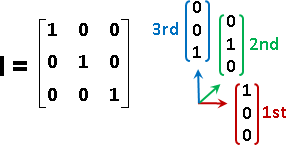
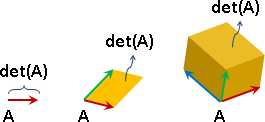
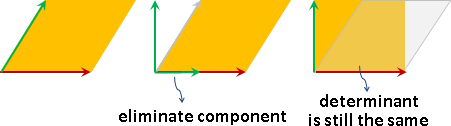
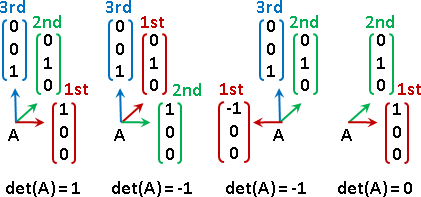
matrix
線性組合可以寫成矩陣乘法的格式。
linear combination x = c₁x₁ + c₂x₂ + ... + cɴxɴ
⎡ | ⎤ ⎡ | | | | ⎤ ⎡ | ⎤
⎢ x ⎥ = ⎢ x₁ x₂ x₃ ... xɴ ⎥ ⎢ c ⎥
⎣ | ⎦ ⎣ | | | | ⎦ ⎣ | ⎦
linear combination y = c₁y₁ + c₂y₂ + ... + cɴyɴ
⎡ | ⎤ ⎡ | | | | ⎤ ⎡ | ⎤
⎢ y ⎥ = ⎢ y₁ y₂ y₃ ... yɴ ⎥ ⎢ c ⎥
⎣ | ⎦ ⎣ | | | | ⎦ ⎣ | ⎦
線性函數可以寫成矩陣乘法的格式。然而輸入被替換成座標了。
linear function f: X -> Y
⎡ | ⎤ ⎡ | | | | ⎤ ⎡ | ⎤
⎢ y ⎥ = ⎢ f(x₁) f(x₂) f(x₃) ... f(xɴ) ⎥ ⎢ c ⎥
⎣ | ⎦ ⎣ | | | | ⎦ ⎣ | ⎦
狹義版本是特例:輸入的座標軸x₁...xɴ恰好是恆等矩陣I。