residue

整數除法：被除數除以除數得到商數與餘數。分堆到底為止。

分堆、補堆任意次數的時候，除數變成模數，餘數變成留數。

餘數只有一個，留數有無限多個。只要隨便求出一個餘數，不斷加減模數，就得到各個留數；各個留數皆平等，任選一個當代表都行，通常是寫最接近零、大於等於零的那一個。一般使用≡全等符號表示各個留數兩兩之間的平等關係。

int quotient = 8 / 3; // 求商數，此運算符號稱作「除」。 int remainder = 8 % 3; // 求餘數，此運算符號稱作「模」。 int quotient = -8 / 3; int remainder = -8 % 3; // 結果是負數，要小心處理。 // 除數為負值，規則詭異，小心使用。 int q = 8 / -3; int r = 8 % -3; int q = -8 / -3; int r = -8 % -3;

中英對照

中文習慣把留數也稱作餘數。以下皆用餘數稱呼留數。

中文習慣把全等改稱作同餘。以下皆用同餘稱呼全等。

dividend   被除數
divisor    除數
quotient   商數
remainder  餘數
modulo     模數
residue    留數→餘數
congruence 全等→同餘

餘數運算

residue是數值。congruence是運算符號。

計算學家重視數值，因此演算法書籍喜愛討論residue；數學家重視性質，因此數學書籍喜愛討論congruence。

實數運算，等於=不是主角，加減乘除才是主角；餘數運算，同餘≡當然也不是主角，加減乘除才是主角。

因此接下來將要討論residue的加減乘除。

modulo mod

餘數無限多個，任選一個當代表都行。

大家習慣選擇最接近零、大於等於零的那一個餘數。

/* a (mod m) , (-∞, +∞) → [0, m) */ int mod(int a, int m) { a %= m; // 模 if (a < 0) a += m; // 小心負數！ return a; } /* a (mod m) , (-∞, +∞) → [0, m) */ int mod(int a, int m) { a %= m; a += a >> 31 & m; // 不使用判斷式！ return a; } /* a (mod m) , [-m, m) → [0, m) */ int upd(int a, int m) { return a += a >> 31 & m; } /* a (mod m) , (-∞, +∞) → [0, m) */ int mod(int a, int m) { return upd(a %= m, m); }

addition +

模數相同時，餘數可相加。

8 (mod 3) + 7 (mod 3) ≡ 15 (mod 3)
8 (mod 3) + 7 (mod 3) + 6 (mod 3) ≡ 21 (mod 3)

模數相同時，mod符號可以精簡成一個，寫在式子後面。

8 + 7 ≡ 15 (mod 3)
8 + 7 + 6 ≡ 21 (mod 3)

餘數加法實際上是「無限多個」加「無限多個」等於「無限多個」。這三項當中，任取一個餘數當代表都行，等式皆成立。然而實際計算時，大可不必想得如此複雜，就是加與模，求得最接近零、大於等於零的那一個餘數。

int n = (8 % 3 + 7 % 3) % 3; // 隨時模，避免溢位。 int n = (8 + 7) % 3; // 先加一加，最後才模。 /* a + b ≡ x (mod m) , a,b ∈ (-∞, +∞) */ int add(int a, int b, int m) { int x = (a % m + b % m) % m; // 隨時模，避免溢位。 if (x < 0) x += m; // 小心負數！ return x; } int add(int a, int b, int m) { // 不使用判斷式！ return (((a % m + b % m) % m) + m) % m; } int add(int a, int b, int m) { return (((a + b) % m) + m) % m; // 先加一加，最後才模。 }

當輸入已經是標準餘數，則可避開模運算，爭取時間。

/* a + b ≡ x (mod m) , a,b ∈ [0, m) */ int add(int a, int b, int m) { // 0 ≤ a,b < m return ((a += b) < m) ? a : (a - m); } int add(int a, int b, int m) { return upd((a += b) -= m, m); }

延伸閱讀：模數不一致的加法

雞肋。窮舉每一種餘數並且相加。

  1 (mod 4) + 1 (mod 6)
≡ ⋯ ∪ 
  { 1 (mod 4) + -5 } ∪ 
  { 1 (mod 4) +  1 } ∪ 
  { 1 (mod 4) +  7 } ∪ 
  ⋯
≡ { 0 (mod 4) } ∪ { 2 (mod 4) }

subtraction −

模數相同時，餘數可相減。

8 - 7 ≡ 1 (mod 3)
8 - 7 - 6 ≡ -5 (mod 3)

/* a − b ≡ x (mod m) , a,b ∈ (-∞, +∞) */ int sub(int a, int b, int m) { return (((a - b) % m) + m) % m; // 先減一減，最後才模。 }

當輸入已經是標準餘數，則可避開模運算，爭取時間。

/* a − b ≡ x (mod m) , a,b ∈ [0, m) */ int sub(int a, int b, int m) { return ((a -= b) < 0) ? (a + m) : a; } int sub(int a, int b, int m) { // 0 ≤ a,b < m return upd(a -= b, m); }

UVa 10787

multiplication ×

餘數可以乘上整數倍率，等同於連加。

8 (mod 5) × 7 ≡ 56 (mod 5)
8 (mod 5) × 7 × 6 ≡ 336 (mod 5)

倍率可以推廣成餘數。換句話說：模數相同時，餘數可相乘。

8 (mod 5) × 7 (mod 5) ≡ 56 (mod 5)
8 (mod 5) × 7 (mod 5) × 6 (mod 5) ≡ 336 (mod 5)

模數相同時，mod符號可以精簡成一個，寫在式子後面。

8 × 7 ≡ 56 (mod 5)
8 × 7 × 6 ≡ 336 (mod 5)

/* a × b ≡ x (mod m) */ int mul(int a, int b, int m) { // 轉型成long long int，避免溢位。 return (int)((long long)a * (long long)b % (long long)m); } int mul(int a, int b, int m) { // 運用隱性轉型，簡化程式碼。 return (long long)a * b % m; } long long mul(long long a, long long b, long long m) { // 無法轉型的時候，只好沿用整數乘法的演算法。 long long x = 0; for (; b > 0; b >>= 1) { if (b & 1) x = add(x, a, m); a = add(a, a, m); } return x; }

exponentiation ^

餘數可以有整數次方，等同於連乘。

8 (mod 3) ^ 3 ≡ 8 (mod 3) × 8 (mod 3) × 8 (mod 3) ≡ 512 (mod 3)

次方值可以推廣成餘數，但是次方值的模數不是原本模數。

模數是質數p，次方值的模數正是p-1。根據「費馬小定理」。
2 (mod 7) ^ 100 ≡ 2 (mod 7) ^ 100 (mod 6)

模數與底數互質，次方值的模數是「Carmichael function λ(m)」其中一個因數。
2 (mod 9) ^ 100 ≡ 2 (mod 9) ^ 100 (mod λ(9))

模數與底數互質，次方值的模數是「coprime counting function φ(m)」其中一個因數。
φ(m)因數種類更多、內含錯誤，但是φ(m)比較容易計算。
2 (mod 9) ^ 100 ≡ 2 (mod 9) ^ 100 (mod φ(9))

模數與底數互質，次方值的模數多半不是m-1其中一個因數。
根據「Lehmer's totient problem」。

模數是普通數字，事情相當複雜，不能直接推廣成餘數，此處不討論。

計算λ(m)和φ(m)曠日廢時。況且我們也不確定是λ(m)和φ(m)的哪一個因數。

如果預先知道λ(m)或φ(m)，就可以預先將次方值模λ(m)或φ(m)，以加速次方運算。

預先知道 φ(9) = 6
  2 (mod 9) ^ 100
≡ 2 (mod 9) ^ 100 (mod φ(9))
≡ 2 (mod 9) ^ 100 (mod 6)
≡ 2 (mod 9) ^ 4 (mod 6)
≡ 16 (mod 9)
≡ 7 (mod 9)

/* a ^ b ≡ x (mod m) */ int pow(int a, int b, int m) { // 沿用整數次方的演算法 int x = 1; for (; b > 0; b >>= 1) { if (b & 1) x = mul(x, a, m); a = mul(a, a, m); } return x; }

UVa 374 luogu P1226

reciprocal ¹⁄ₓ

求乘數，乘積是1。

☐ × 7 ≡ 1 (mod 5)

移項即是倒數。

1 ÷ 7 ≡ ☐ (mod 5)   除法風格
¹⁄₇   ≡ ☐ (mod 5)   分數風格
7⁻¹   ≡ ☐ (mod 5)   次方風格
7     ≡ ☐ (mod 5)   共軛風格

餘數倒數要嘛無解、要嘛無限多解。如果只看大於等於零、小於模數的答案數量，餘數倒數可能無解、一解。

☐ × 7 ≡ 1 (mod 5)   —→  1 ÷ 7 ≡ ☐ (mod 5)   ☐是3
3 × ☐ ≡ 1 (mod 4)   —→  1 ÷ 3 ≡ ☐ (mod 4)   ☐是3
2 × ☐ ≡ 1 (mod 4)   —→  1 ÷ 2 ≡ ☐ (mod 4)   ☐不存在
1 × ☐ ≡ 1 (mod 4)   —→  1 ÷ 1 ≡ ☐ (mod 4)   ☐是1
0 × ☐ ≡ 1 (mod 4)   —→  1 ÷ 0 ≡ ☐ (mod 4)   ☐不存在

實數倒數、餘數倒數，意義不同！實數倒數的本質是「等分」，餘數倒數不具備這種意義。餘數倒數的本質是乘法式子解未知數。

實數倒數、餘數倒數，算法不同！實數倒數的演算法是「長除法」。餘數倒數的演算法是「輾轉相除法」。

倒數的定義
a × a ≡ 1 (mod m)

上式重新整理（上式只取其中一個餘數當代表，現在則是考慮所有餘數。）
a × a + m × k = 1

使用擴展版本的輾轉相除法，求得a與m的最大公因數，求得倍率a與k，得到我們想要的「a的倒數」。

a與m的最大公因數必須是一（互質），才擁有倒數。

換句話說。模數是質數：每一個數都有倒數。模數不是質數：只有跟模數互質的數才有倒數。

/* a × x ≡ 1 (mod m) */ int rec(int a, int m) { int d = m, x = 0, y = 1; while (a != 0) { int q = d / a, r = d % a; d = a; a = r; int t = x - q * y; x = y; y = t; } if (d != 1) return -1; // 沒有倒數 return upd(x, m); // 小心負數！ } /* ax + by = d */ void extgcd(int a, int b, int& x, int& y, int& d) { if (!b) {x = 1; y = 0; d = a; return;} gcd(b, a%b, y, x, d); y -= (a / b) * x; } /* a × x ≡ 1 (mod m) */ int rec(int a, int m) { int d, x, y; extgcd(a, m, x, y, d); return d == 1 ? upd(x, m) : -1; }

luogu P1082

reciprocal table ¹⁄₁ ... ¹⁄ₓ（模數是質數）

模數是質數，每一個數都有倒數！

此時可以預先建立倒數表，預先計算每一個數的倒數。利用遞迴公式，時間複雜度O(N)。

 p % i = p - floor(p ÷ i) × i
 p % i ≡   - floor(p ÷ i) × i          (mod p)
rec[i] ≡   - floor(p ÷ i) × rec[p % i] (mod p)   移項

int rec[100]; void reciprocal_table(int p) { rec[1] = 1; for (int i=2; i<p; ++i) rec[i] = (p - (p/i) * rec[p%i] % p) % p; }

reciprocal ¹⁄ₓ（模數是質數）

根據「費馬小定理」，模數是質數p，倒數恰是p-2次方。

不必特地撰寫輾轉相除法。時間複雜度也差不多。

a ^ p     ≡ a (mod p)
a ^ (p-1) ≡ 1 (mod p)   when a ≢ 0 (mod p)
a ^ (p-2) ≡ a (mod p)   when a ≢ 0 (mod p)

/* a × x ≡ 1 (mod m) , m is prime */ int rec(int a, int m) { return pow(a, m-2, m); }

division ÷

求乘數（被乘數）。

☐ × 7 ≡ 22 (mod 5)

移項即是除法。

22 ÷ 7 ≡ ☐ (mod 5)

餘數除法要嘛無解、要嘛無限多解。如果只看大於等於零、小於模數的答案數量，餘數除法可能無解、一解、多解。

☐ × 7 ≡ 22 (mod 5)  —→  22 ÷ 7 ≡ ☐ (mod 5)  ☐是1
☐ × 2 ≡ 3 (mod 4)   —→  3 ÷ 2 ≡ ☐ (mod 4)   ☐不存在
☐ × 4 ≡ 5 (mod 10)  —→  5 ÷ 4 ≡ ☐ (mod 10)  ☐不存在
☐ × 3 ≡ 0 (mod 6)   —→  0 ÷ 3 ≡ ☐ (mod 6)   ☐是0或2
☐ × 3 ≡ 3 (mod 12)  —→  3 ÷ 3 ≡ ☐ (mod 12)  ☐是1或5或9

究竟如何計算餘數除法呢？數學家發明了倒數！

☐ × 7      ≡ 22     (mod 5)   求乘數
☐ × 7 × 7  ≡ 22 × 7 (mod 5)   等號兩側同乘以「7的倒數」
☐          ≡ 22 × 7 (mod 5)   「7」乘以「7的倒數」令它是1，就能消掉。
22 ÷ 7 ≡ ☐ ≡ 22 × 7 (mod 5)   「除以7」變成「乘以7的倒數」

數學家利用等量乘法原理，建立了倒數的概念。數學家規定：原數與倒數相乘等於1。因此「除以原數」變成「乘以倒數」，解決了看似無法整除的情況。

預先求出倒數，便可計算餘數除法！

7 ≡ 3 (mod 5)   模5的時候，7的倒數是3。因為 7 × 3 ≡ 1 (mod 5)。

22 ÷ 7 ≡ 22 × 7 ≡ 22 × 3 ≡ 66 ≡ 1 (mod 5)
 3 ÷ 7 ≡  3 × 7 ≡  3 × 3 ≡  9 ≡ 4 (mod 5)
 2 ÷ 7 ≡  2 × 7 ≡  2 × 3 ≡  6 ≡ 1 (mod 5)
 1 ÷ 7 ≡  1 × 7 ≡  1 × 3 ≡  3 ≡ 3 (mod 5)

/* a ÷ b ≡ x (mod m) , a ⊥ m */ int div(int a, int b, int m) { // a ÷ b ≡ a × b̅ (mod m) return mul(a, rec(b, m), m); }

原數與模數互質，可以求得倒數。

原數與模數不互質，必須不斷約分，直到互質：

一、a b m一齊約掉三者公因數d，答案不變。

二、b m一齊約掉兩者公因數d，a卻無法約掉d，無解。

三、模數m/d還原成模數m，答案不變。

四、模數m範圍之內有d個答案，記得補寫其他d-1個餘數。

簡易方式是計算d = gcd(b,m)，一口氣約分到底，直接互質。

a   ÷ b   ≡ ☐ (mod m)
a/d ÷ b/d ≡ ☐ (mod m/d)

/* a ÷ b ≡ x (mod m) */ vector<int> div(int a, int b, int m) { int d = gcd(b, m); if (a % d != 0) return {}; // 無解 a /= d; b /= d; m /= d; // 約分 int x = mul(a, rec(b, m), m); // 正解 // 還原模數，1個餘數變成d個餘數。 vector<int> v(d); v[0] = x; for (int i=1; i<d; ++i) { x += m; v[i] = x; } return v; }

luogu P2613

linear congruence ax ≡ b (mod m)

餘數一元一次方程式＝餘數除法。

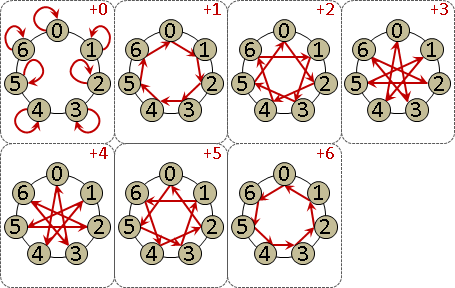
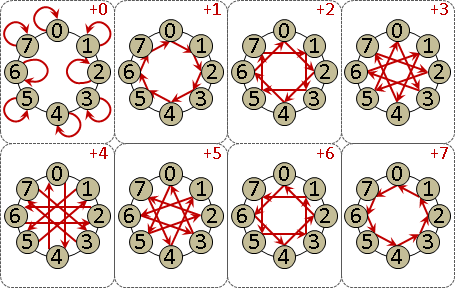
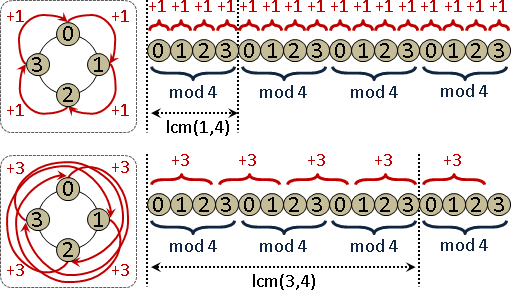
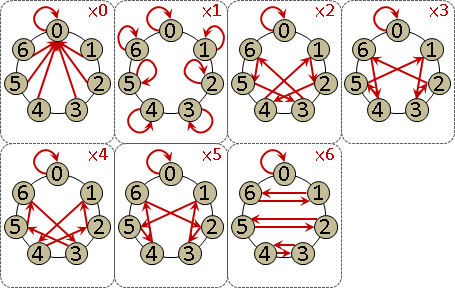
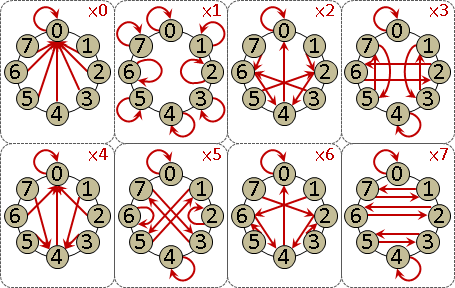
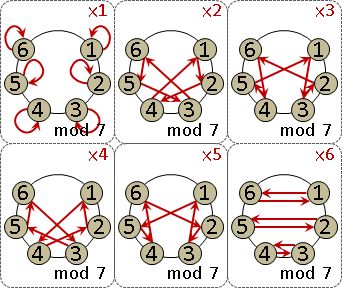
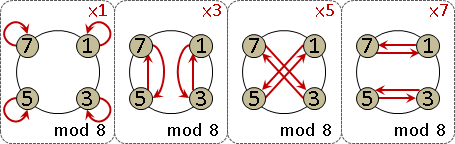
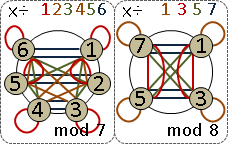
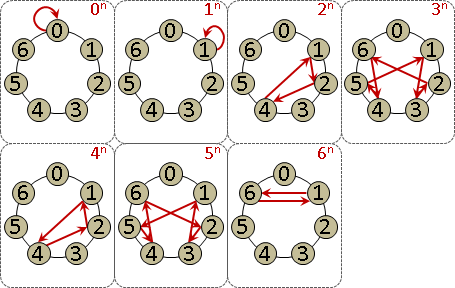
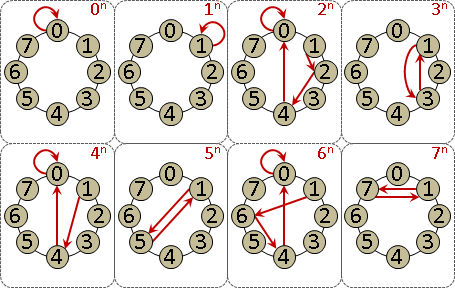
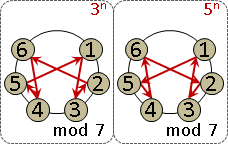
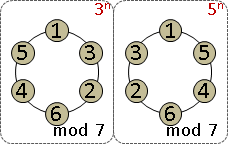
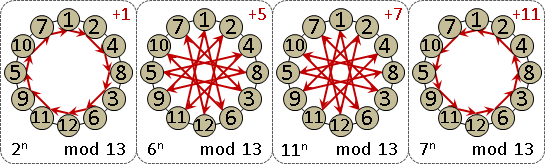
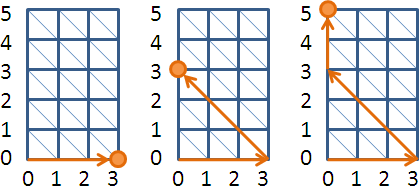
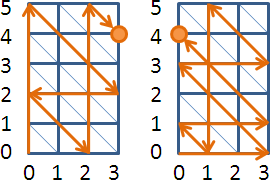
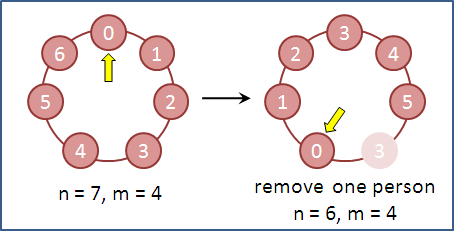
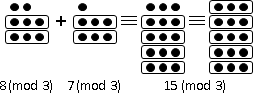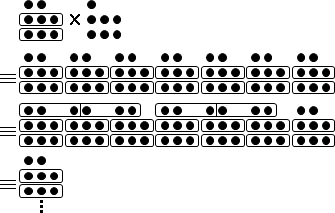monic linear congruences x ≡ rᵢ (mod mᵢ) , mᵢ are coprime

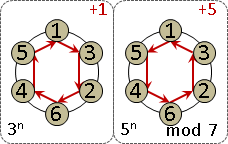
南北朝數學著作《孫子算經》有一道題目：今有物不知其數，三三數之賸二，五五數之賸三，七七數之賸二，問物幾何？

用現代數學術語來說，這個問題就是餘數系統的一元一次方程組，而且係數皆是一，而且模數兩兩互質。

{ x ≡ 2 (mod 3)
{ x ≡ 3 (mod 5)
{ x ≡ 2 (mod 7)

正確答案是105數之賸23。

x ≡ 23 (mod 105)

演算法是「Garner's algorithm」、「Qin's algorithm」。

演算法（窮舉法）

窮舉法：列出「三三數之賸二」的數字，然後是「五五數之賸三」與「七七數之賸二」。三個列表都出現的數字，就是正確答案。

{ x ≡ 2 (mod 3)  ⇔  x = ..., 8, 5, 2, -1, -4, ...
{ x ≡ 3 (mod 5)  ⇔  x = ..., 13, 8, 3, -2, -7, ...
{ x ≡ 2 (mod 7)  ⇔  x = ..., 16, 9, 2, -5, -12, ...

試誤法：一一列出各種答案，試著除以三、五、七。

不幸的是，答案有無限多個，試誤法無法找到所有答案。然而試誤法讓我們發現答案具有規律。

void solve() { for (int x=-1000; x<=+1000; ++x) if (x % 3 == 2 && x % 5 == 3 && x % 2 == 7) cout << x; }

演算法（Garner's algorithm）

遞推法：逐式代入求解。

{ x ≡ 2 (mod 3) 
{ x ≡ 3 (mod 5)
{ x ≡ 2 (mod 7)

最初 x ≡ 2 (mod 3)
⇒ x = 3t + 2

代入 x ≡ 3 (mod 5)
⇒ 3t + 2 ≡ 3 (mod 5) ⇒ 3t ≡ 1 (mod 5) ⇒ t ≡ 2 (mod 5)
⇒ t = 5s + 2
代回 x = 3t + 2
⇒ x = 3(5s + 2) + 8 = 15s + 8

代入 x ≡ 2 (mod 7)
⇒ 15s + 8 ≡ 2 (mod 7) ⇒ 15s ≡ 1 (mod 7) ⇒ s ≡ 1 (mod 7)
⇒ s = 7u + 1
代回 x = 15s + 8
⇒ x = 15(7u + 1) + 8 = 105u + 23

換句話說：每次只算兩道式子，重複N-1次。

一、一元一次方程組，係數皆是一，模數 m₁ m₂ 互質。
{ x ≡ r₁ (mod m₁)
{ x ≡ r₂ (mod m₂)

二、令一式成立。處理 x 模 m₁。
x ≡ r₁ + k m₁ (mod m₁)

三、令二式也成立。處理 x 模 m₂。
x ≡ r₁ + k m₁ ≡ r₂           (mod m₂)
         k m₁ ≡ r₂ - r₁      (mod m₂)
         k    ≡ (r₂ - r₁) m₁ (mod m₂)

四、得到答案。《linear interpolation》
{ x ≡ r₁ + k m₁ (mod m₁)     where k ≡ (r₂ - r₁) m₁ (mod m₂)
{ x ≡ r₁ + k m₁ (mod m₂)

五、模數統一設定成最小公倍數，恰是 m₁m₂。
x ≡ r₁ + k m₁ (mod m₁m₂)     where k ≡ (r₂ - r₁) m₁ (mod m₂)

/* x ≡ rᵢ (mod mᵢ) , mᵢ are coprime */ int solve(int r[], int m[], int N) { int x = r[0]; // r₁ int M = m[0]; // m₁ for (int i=1; i<N; i++) { int dr = sub(r[i], x % m[i], m[i]); // r₂ - r₁ int k = div(dr, M, m[i]); // k ≡ (r₂ - r₁) m̅₁ x += k * M; // x ≡ r₁ + k m₁ M *= m[i]; // x (mod m₁m₂) x %= M; } return x; }

演算法（Qin's algorithm）（Gauss' algorithm）

公式解：宋朝數學著作《數書九章》發明的「大衍總數術」。

一、一元一次方程組，係數皆是一，模數 m₁ 到 mɴ 兩兩互質。
　　{ x ≡ r₁ (mod m₁)
　　{ ⋮
　　{ x ≡ rɴ (mod mɴ)

二、令 M = m₁ × m₂ × ... × mɴ
　　　 M₁ = M ÷ m₁
　　　 ⋮
　　　 Mɴ = M ÷ mɴ

　　Mᵢ 原本包含所有模數，但是刻意消去了 mᵢ。
　　造成 Mᵢ 只對其中一個模數 mᵢ 有反應（無法整除）（互質）：
　　Mᵢ % mⱼ ≠ 0   when i = j
　　Mᵢ % mⱼ = 0   when i ≠ j

三、令 M₁ = M₁的倒數，模數為 m₁
　　　 ⋮
　　　 Mɴ = Mɴ的倒數，模數為 mɴ

　　讓 (Mᵢ × Mᵢ) 只對其中一個模數 mᵢ 有反應，得到結果是 1：
　　(Mᵢ × Mᵢ) % mⱼ = 1   when i = j
　　(Mᵢ × Mᵢ) % mⱼ = 0   when i ≠ j

　　再讓 (rᵢ × Mᵢ × Mᵢ) 只對其中一個模數 mᵢ 有反應，得到結果是 rᵢ。
　　(rᵢ × Mᵢ × Mᵢ) % mⱼ = rᵢ   when i = j
　　(rᵢ × Mᵢ × Mᵢ) % mⱼ = 0    when i ≠ j

四、N道式子通通加起來，以滿足方程組。《Lagrange interpolation》
　　x ≡ (r₁ × M₁ × M₁) (mod m₁) + ... + (rɴ × Mɴ × Mɴ) (mod mɴ) 

五、模數統一設定成最小公倍數，恰是 M。
　　x ≡ (r₁ × M₁ × M₁) + ... + (rɴ × Mɴ × Mɴ) (mod M)

const int N = 3; int r[N] = {2, 3, 2}; int m[N] = {3, 5, 7}; /* x ≡ rᵢ (mod mᵢ) , mᵢ are coprime */ int solve(int r[], int m[], int N) { int M = 1; for (int i=0; i<N; ++i) M *= m[i]; int x = 0; for (int i=0; i<N; ++i) { int a = mul(r[i], M/m[i], M); int b = rec(M/m[i], m[i]); int n = mul(a, b, M); x = add(x, n, M); } return x; }

monic linear congruences x ≡ rᵢ (mod mᵢ)

一道方程式拆解成多道方程式，原模數等於新模數的最小公倍數，答案不變。

                     { x ≡ 4 (mod 9)
x ≡ 4 (mod 360)  —→  { x ≡ 4 (mod 10)
                     { x ≡ 4 (mod 24)

where 360 = lcm(9, 10, 24)

一道方程式，實施分割，讓模數互質：

原模數做質因數分解，新模數是質因數次方。

                     { x ≡ 4 (mod 2³)
x ≡ 4 (mod 360)  —→  { x ≡ 4 (mod 3²)
                     { x ≡ 4 (mod 5¹)

where 360 = 2³ × 3² × 5¹ = lcm(2³, 3², 5¹)

多道方程式，實施合併，讓模數互質：

一、模數相同，餘數不同，顯然無解。

二、模數都是同一個質數p的各種次方，餘數可以重新視作p進位。位數一致：合併對應位數。位數不一致：無解。

原模數是質數p的各種次方，新模數是質數p的最高次方。

                      { x ≡ 2 (mod 2²)✔ 10₍₂₎
{ x ≡ 2 (mod 4)       { x ≡ 6 (mod 3¹)  
{ x ≡ 6 (mod 48)  —→  { x ≡ 6 (mod 2⁴)✔110₍₂₎
{ x ≡ 4 (mod 360)     { x ≡ 4 (mod 2³)✔100₍₂₎
                      { x ≡ 4 (mod 3²)   ↑
                      { x ≡ 4 (mod 5¹)   no solution

                      { x ≡ 1 (mod 2²)✔  1₍₂₎
{ x ≡ 1 (mod 4)       { x ≡ 7 (mod 3¹)             { x ≡ 7 (mod 2⁴)
{ x ≡ 7 (mod 48)  —→  { x ≡ 7 (mod 2⁴)✔111₍₂₎  —→  { x ≡ 1 (mod 3²)
{ x ≡ 1 (mod 360)     { x ≡ 1 (mod 2³)✔  1₍₂₎      { x ≡ 1 (mod 5¹)
                      { x ≡ 1 (mod 3²)
                      { x ≡ 1 (mod 5¹)

方程組變成了上個小節的格式。

/* x ≡ rᵢ (mod mᵢ) */ int solve(int r[], int m[], int N) { // x ≡ r₁ + (r₂ - r₁) m̅₁ m₁ (mod m₂) int x = r[0]; // r₁ int M = m[0]; // m₁ for (int i=1; i<N; i++) { int dr = sub(r[i], x % m[i], m[i]); // r₂ - r₁ int s, t, d; extgcd(M, m[i], s, t, d); // gcd(b, m) if (dr % d) return -1; // 無解 // s = upd(s, m[i]); // m̅₁ (mod m₂) // int k = mul(s % m[i]/d, dr/d, m[i]/d); // 約分 s = mod(s, m[i]/d); int k = mul(s, dr/d, m[i]/d); x += k * M; // x = r₁ + k m₁ M *= m[i]/d; // x (mod lcm(m₁,m₂)) x %= M; } return x; }

luogu P4777

linear congruences aᵢx ≡ bᵢ (mod mᵢ)

一道方程式，係數和模數剛好互質，運用倒數、消去係數。

一道方程式，係數和模數沒有互質，不斷約分、直到互質。

{ 1x ≡ 2 (mod 3)      { x ≡ 1×2 (mod 3)      { x ≡ 2 (mod 3)
{ 3x ≡ 3 (mod 5)  —→  { x ≡ 3×3 (mod 5)  —→  { x ≡ 6 (mod 5)
{ 5x ≡ 2 (mod 7)      { x ≡ 5×2 (mod 7)      { x ≡ 6 (mod 7)

方程組變成了上個小節的格式。

Chinese remainder theorem

模數之於中國餘數定理，猶如質數之於算術基本定理。

凡是餘數r，都可以藉由一元一次方程組、係數為一、模數互質，成為一個獨一無二的餘數組(r₁, r₂, ...)。

但是前提是特定的模數m、模數組(m₁, m₂, ...)：

條件一、模數組乘積必須等於模數m = m₁m₂...。

條件二、模數組必須兩兩互質mᵢ⊥mⱼ。

一種方式是m做質因數分解，mᵢ是每一項質因數次方。

一元一次方程組、係數為一、模數互質
{ r ≡ r₁ (mod m₁)
{ r ≡ r₂ (mod m₂)   where mᵢ⊥mⱼ
{ :   :    :  :

中國餘數定理：一維餘數與多維餘數的一對一轉換
r (mod m₁m₂...)  ←—→  (r₁ (mod m₁), r₂ (mod m₂), ...)

這樣比較好讀
    (m₁, m₂, ...)
r  ←—————————————→  (r₁, r₂, ...)

一元一次方程組、係數為一、模數互質
{ 10 ≡ 1 (mod 3)
{ 10 ≡ 0 (mod 5)
{ 10 ≡ 3 (mod 7)

中國餘數定理：一維餘數與多維餘數的一對一轉換
10 (mod 3×5×7)  ←—→  (1 (mod 3), 0 (mod 5), 3 (mod 7))

這樣比較好讀
     (3,5,7)
10  ←———————→  (1,0,3)

    已知一組模數，分別計算餘數。O(N)
r  —————————————————————————————————→  (r₁, r₂, ...)
   ←—————————————————————————————————
           解方程組。O(Nlog(m))

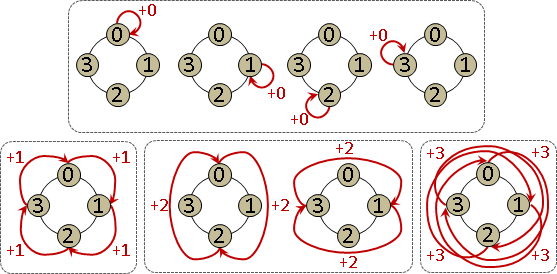
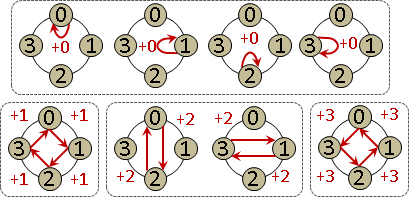
根據中國餘數定理，一維餘數的運算，等同多維餘數的運算。

分解前  模數 105 | 分解後                     模數 (3, 5, 7)
5                | (2, 0, 5)
9                | (0, 4, 2)
-----------------+------------------------------------------
5 + 9 ≡ 14       | (2+0, 0+4, 5+2) ≡ (2, 4, 7)
5 - 9 ≡ -4 ≡ 101 | (2-0, 0-4, 5-2) ≡ (2, -4, 3) ≡ (2, 1, 3)
5 × 9 ≡ 45       | (2×0, 0×4, 5×2) ≡ (0, 0, 10)
5 ÷ 9 ≡ undefine | (2÷0, 0÷4, 5÷2) ≡ undefine
5 ÷ 8 ≡ 40       | (2÷2, 0÷3, 5÷1) ≡ (1, 0, 5)
5 ^ 2 ≡ 25       | (2^2, 0^2, 5^2) ≡ (4, 0, 25) ≡ (1, 0, 4)

UVa 756 700 11754

整數系統與餘數系統互相轉換

介紹一個重要的計算技巧：一段整數的計算流程，改為套上各種模數並且分別計算答案，最後運用中國餘數定理還原正確答案──先換到餘數系統，再還原為整數系統。

(999 + 25) × 333 ÷ 256 = ?

採用互質的模數3、5、11，聯立
{ (999 + 25) × 333 ÷ 256 ≡ (0 + 1) × 0 ÷ 1 ≡ 0 (mod 3)
{ (999 + 25) × 333 ÷ 256 ≡ (-1 + 0) × 3 ÷ 1 ≡ 2 (mod 5)
{ (999 + 25) × 333 ÷ 256 ≡ (9 + 3) × 3 × 4 ≡ 1 × 1 ≡ 1 (mod 11)

再運用中國餘數定理
=> (999 + 25) × 333 ÷ 256 ≡ 12 (mod 165)

999+25是4位數，333是3位數，256是3位數，推測正確答案是4位數：
12 + 165 × 6 = 1002
1002 + 165 = 1167
1167 + 165 = 1332
......

一、當數字很大、式子很長時，此技巧就能發揮功效！

二、模數們最好兩兩互質，方便套用中國餘數定理。

三、此技巧得到的答案一定是整數；也就是說，當正確答案是整數，才能使用此技巧。比如說，式子之中有除法，導致正確答案是分數，此時就不能使用此技巧。

四、式子之中若有除法，則令模數是質數，餘數除法保證有唯一解。承第二點，也就是說，模數們最好都是質數。

五、選定的模數們，其乘積足夠大，大於正確答案時，那麼最後求得的餘數，即是正確答案，不必再推測。

例如求「Hilbert matrix」的反矩陣。Hilbert matrix由單位分數組成，其反矩陣恰好都是整數。先將問題轉換成餘數系統，選擇多個模數並且各別以高斯消去法求得反矩陣，最後再用中國餘數定理轉換回整數系統。

multiplicative order ord()

求指數，乘冪是1。

2 ^ ☐ ≡ 1 (mod 9)

移項即是乘性階。

ord₉(2) = ☐

餘數乘性階擁有無限多解。如果只看大於等於零、小於模數的答案數量，餘數乘性階至少一解0。

數學家只取最小正數──次方值的模數。

0 ^ ☐ ≡ 1 (mod 9)  —→  ord₉(0) = ☐   ☐是0            	→未定義
1 ^ ☐ ≡ 1 (mod 9)  —→  ord₉(1) = ☐   ☐是0...8        	→只取1
2 ^ ☐ ≡ 1 (mod 9)  —→  ord₉(2) = ☐   ☐是0或6         	→只取6
3 ^ ☐ ≡ 1 (mod 9)  —→  ord₉(3) = ☐   ☐是0            	→未定義
4 ^ ☐ ≡ 1 (mod 9)  —→  ord₉(4) = ☐   ☐是0或3或6      	→只取3
5 ^ ☐ ≡ 1 (mod 9)  —→  ord₉(5) = ☐   ☐是0或6         	→只取6
6 ^ ☐ ≡ 1 (mod 9)  —→  ord₉(6) = ☐   ☐是0            	→未定義
7 ^ ☐ ≡ 1 (mod 9)  —→  ord₉(7) = ☐   ☐是0或3或6      	→只取3
8 ^ ☐ ≡ 1 (mod 9)  —→  ord₉(8) = ☐   ☐是0或2或4或6或8	→只取2

實數乘性階、餘數乘性階，意義不同！實數乘性階是0，缺乏討論意義。餘數乘性階是次方值的模數。

底數與模數互質，才擁有乘性階。如同倒數。

換句話說。模數是質數：每一個數都有乘性階。模數不是質數：只有跟模數互質的數才有乘性階。

試誤法：窮舉次方值。O(m)。

/* a ^ x ≡ 1 (mod m) */ int ord(int a, int m) { for (int x=1; x<m; ++x) if (pow(a, x, m) == 1) return x; return -1; // 無解 } /* a ^ x ≡ 1 (mod m) */ int ord(int a, int m) { int ax = 1; for (int x=1; x<m; ++x) { ax = mul(ax, a, m); if (ax == 1) return x; } return -1; // 無解 }

試誤法：窮舉次方值。窮舉λ(m)的因數。λ(m)計算時間較長，改成窮舉φ(m)的因數。O(sqrt(m))。

/* φ(n) = n × (1 - 1/p₁) × (1 - 1/p₂) × ... */ int phi(int n) { int c = n; for (int p=2; p*p<=n; p++) if (n % p == 0) { while (n % p == 0) n /= p; c -= c / p; } if (n > 1) c -= c / n; return c; } /* a ^ x ≡ 1 (mod m) */ int ord(int a, int m) { if (gcd(a, m) != 1) return -1; // 無解 // 窮舉φ(m)的因數 int phi_m = phi(m); for (int d=1; d*d<=phi_m; ++d) if (phi_m % d == 0 && pow(a, d, m) == 1) return d; return phi_m; } /* a ^ x ≡ 1 (mod m) */ int ord(int a, int m) { if (gcd(a, m) != 1) return -1; // 無解 int phi_m = phi(m), an = 1; for (int d=1; d*d<=phi_m; ++d) { an = mul(an, a, m); if (an == 1) return d; } return phi_m; }

試除法：窮舉φ(m)的因數。時間複雜度我不會算。

一、解的因數不是解。改成從大到小窮舉因數。

二、解的倍數也是解（若是φ(m)的因數）。改成由小到大窮舉倍數，φ(m)除以倍數得到因數。宛如逐步消滅φ(m)的質因數。

/* p₁^e₁ × p₂^e₂ × ... */ typedef vector<pair<int,int>> Factor; /* n = p₁^e₁ × p₂^e₂ × ... */ Factor factorize(int n) { Factor fac; for (int p=2; p*p<=n; ++p) { int e = 0; while (n % p == 0) { n /= p; e++; } if (e > 0) fac.push_back({p, e}); } if (n > 1) fac.push_back({n, 1}); return fac; } /* φ(n) = n × (1 - 1/p₁) × (1 - 1/p₂) × ... */ int phi(int n) { Factor fac = factorize(n); for (int i=0; i<(int)fac.size(); i++) n -= n / fac[i].first; return n; } /* a ^ x ≡ 1 (mod m) */ int ord(int a, int m) //tuple<int,Factor> ord(int a, int m) { if (gcd(a, m) != 1) return -1; // 無解 // if (gcd(a, m) != 1) return {-1, {}}; int n = phi(m); Factor fac = factorize(n); // int N = 0; // factorize(order) size // 窮舉φ(m)的因數 for (int i=0; i<(int)fac.size(); i++) { int& p = fac[i].first; int& e = fac[i].second; while (n % p == 0 && pow(a, n/p, m) == 1) { n /= p; e--; } // if (e > 0) fac[N++] = fac[i]; } return n; // return {n, fac}; // order and factorize(order) }

discrete logarithm log() / index ind()

求指數。

2 ^ ☐ ≡ 7 (mod 9)

移項即是對數。

ind₂(7 (mod 9)) ≡ ☐ (mod ord₉(2))

餘數對數屬於NP問題，但是目前還不確定它究竟是P問題或是NP-complete問題，相當特別。

餘數對數的演算法是「baby-step giant-step algorithm」、「Pohlig–Hellman algorithm」。

UVa 10225 11916 luogu P4195

演算法（baby-step giant-step algorithm）

簡單起見，首先討論底數與模數互質的情況。

試誤法。a⁰到aᵐ⁻¹依序分為⌈m/n⌉個區塊，一個區塊有n個數字。第一區塊採用窮舉法，其餘區塊採用記憶法。

a ^ x ≡ b (mod m)   已知a b m，求x。另外a ⊥ m。

一、隨便選一個正整數n。（通常是sqrt(m)）
二、baby-step，一步一個數字，總共n步，第一區塊：
　甲、計算a⁰, a¹, ..., aⁿ⁻¹，
　　　如果等於b，就找到答案了。
三、giant-step，一步n個數字，總共(⌈m/n⌉ - 1)步，其餘區塊：
　甲、一口氣處理aⁿ到a²ⁿ⁻¹：
　　　　aⁿ⁺ⁱ ≡ b
　　　　aⁿ × aⁱ ≡ b
　　　　aⁱ ≡ b × rec(aⁿ)
　　　先前計算的a⁰, a¹, ..., aⁿ⁻¹，
　　　如果等於b × rec(aⁿ)，就找到答案了。
　乙、一口氣處理a²ⁿ到a³ⁿ⁻¹，
　　　　a²ⁿ⁺ⁱ ≡ b
　　　　aⁿ × aⁿ × aⁱ ≡ b
　　　　aⁱ ≡ b × rec(aⁿ) × rec(aⁿ)
　　　先前計算的a⁰, a¹, ..., aⁿ⁻¹，
　　　如果等於b × rec(aⁿ) × rec(aⁿ)，就找到答案了。
　丙、如法炮製。

採用array儲存a⁰到aⁿ⁻¹，索引儲存，空間複雜度O(m)。baby-step時間複雜度O(n)，gaint-step時間複雜度O(m/n)，總時間複雜度O(n + m/n)。令n = sqrt(m)讓時間複雜度達到最低，成為O(sqrt(m))。

採用binary search tree儲存a⁰到aⁿ⁻¹，空間複雜度降為O(n)，時間複雜度升為O(n + (m/n) ⋅ log(n))。

採用hash table儲存a⁰到aⁿ⁻¹，應付模數m很大的情況。

大量計算相同底數與模數的log，不必重算baby-step，總時間複雜度O(n + N(m/n))。根據計算次數N來升高n，讓時間複雜度達到最低。

/* a ^ x ≡ b (mod m) , a ⊥ m */ int ind(int a, int b, int m) { if (b == 1) return 0; // 儲存a⁰ ... aⁿ⁻¹ vector<int> x(m, -1); // associative array // map<int, int> x; // red-black tree // unordered_map<int, int> x; // hash table // baby-step: a⁰ ... aⁿ⁻¹ int n = sqrt(m); int ai = 1; for (int i=0; i<n; ++i) { if (ai == b) return i; if (x[ai] == -1) x[ai] = i; // if (!x.count(ai)) x[ai] = i; ai = mul(ai, a, m); } // gaint-step: (aⁿ ... a²ⁿ⁻¹) (a²ⁿ ... a³ⁿ⁻¹) ...... int rec_an = rec(ai, m); for (int i=n; i<m; i+=n) { b = mul(b, rec_an, m); if (x[b] != -1) return i + x[b]; // if (x.count(b)) return i + x[b]; } return -1; // 無解 }

改變移項方式，避免計算倒數。缺點是不支援大量計算。

二、baby-step，一步一個數字，總共n步，第一區塊：
　甲、處理a⁰到aⁿ⁻¹：
　　　　aⁱ ≡ b
　　　　aⁿ ≡ b × aⁿ⁻ⁱ
　　　計算baⁿ, ..., ba², ba¹，
　　　如果等於aⁿ，就找到答案了。
三、giant-step，一步n個數字，總共⌈m/n⌉步，全部區塊：
　甲、一口氣處理aⁿ到a²ⁿ⁻¹：
　　　　aⁿ⁺ⁱ ≡ b
　　　　a²ⁿ  ≡ b × aⁿ⁻ⁱ
　　　先前計算的baⁿ, ..., ba², ba¹，
　　　如果等於a²ⁿ，就找到答案了。
　乙、如法炮製。

/* a ^ x ≡ b (mod m) , a ⊥ m */ int ind(int a, int b, int m) { vector<int> x(m, -1); int n = sqrt(m); int ai = 1, aq = 1; for (int i=0; i<n; ++i) { ai = mul(ai, a, m); x[mul(ai, b, m)] = i; // baby-step的檢查步驟挪到gaint-step，精簡程式碼。 } for (int i=0; i<m; i+=n) { aq = mul(aq, ai, m); if (x[aq] != -1) return i + (n-1 - x[aq]); } return -1; }

接著討論底數與模數不互質的情況。

約分。a的次方提出一項，以便約分。不斷提項，約分到底。紀錄總共提出幾項，最後計入答案。

/* a ^ x ≡ b (mod m) */ int ind(int a, int b, int m) { if (b == 1) return 0; // 約分 int c, d, aq = 1; for (c=0; (d = gcd(a, m)) != 1; c++) { if (b % d != 0) return -1; b /= d; m /= d; aq = mul(aq, a/d, m); if (b == aq) return c + 1; } // 小步大步 vector<int> x(m, -1); int n = sqrt(m); int ai = 1; for (int i=0; i<n; ++i) { ai = mul(ai, a, m); x[mul(ai, b, m)] = i; } for (int i=0; i<m; i+=n) { aq = mul(aq, ai, m); // 加回c if (x[aq] != -1) return i + (n-1 - x[aq]) + c; } return -1; }

演算法（Pohlig–Hellman algorithm）

當次方的模數很大，利用中國餘數定理，將一個大模數改成多個小模數，小模數是質因數次方。

當次方的新模數仍然很大，利用「多項式求係數」演算法原理，將一個大模數改成多個小模數，小模數是質因數的每種次方。新餘數視作p進位，從最低位數開始計算，一模一除求得每個位數。

時間複雜度O(sum(pₖ + eₖ log(m)))。pₖ和eₖ來自次方的模數的質因數分解ord(m) = p₁^e₁ × p₂^e₂ × ...。

當次方的新新模數仍然很大，利用小步大步演算法加速。

/* a ^ x ≡ b (mod m) , a ⊥ m */ int ind(int a, int b, int m) { int n; // order Factor fac; // factorize(order) tie(n, fac) = ord(a, m); int N = fac.size(); vector<pair<int,int>> rm(N); // linear congruences for (int k=0; k<N; k++) { int p = fac[k].first; int e = fac[k].second; // a^(0n/p), a^(1n/p), a^(2n/p), ... unordered_map<int, int> x; int wn = 1; int w = pow(a, n/p, m); for (int i=0; i<p; ++i) { if (!x.count(wn)) x[wn] = i; wn = mul(wn, w, m); } int num = n, rhs = b; int value = 0, digit, pn = 1; for (int i=0; i<e; ++i) { num /= p; wn = pow(rhs, num, m); if (!x.count(wn)) return -1; digit = x[wn] * pn; value += digit; pn *= p; // rhs ÷ (a ^ digit) ≡ rhs × (a ^ -digit) rhs = mul(rhs, pow(a, n-digit%n, m), m); } rm[k] = {value, pn}; } return solve(rm); // x ≡ rᵢ (mod mᵢ) }

root of unity √n1

求底數，乘冪是1。

☐ ^ 3 ≡ 1 (mod 9)

移項即是單位根。

∛1 ≡ ☐ (mod 9)

試誤法：窮舉所有底數。

/* x ^ n ≡ 1 (mod m) */ vector<int> roots_of_unity(int n, int m) { vector<int> v; for (int x=1; x<m; x++) if (pow(x, n, m) == 1) v.push_back(x); return v; }

nth root √n‾

求底數。

☐ ^ 3 ≡ 7 (mod 9)

移項即是開方。

∛7 ≡ ☐ (mod 9)

餘數開方是否有解：次方值約分、費馬小定理。

如果乘冪與模數不互質，那麼我就不知道該怎麼辦了。

/* x ^ a ≡ b (mod m) , b ⊥ m */ bool has_root(int a, int b, int m) { if (b == 0) return true; int phi_m = phi(m); int d = gcd(a, phi_m); return pow(b, phi_m / d, m) == 1; }

餘數開方屬於NP-complete問題。

餘數開方的演算法是「Adleman–Manders–Miller algorithm」、「Williams' algorithm」。

ICPC 4746 luogu P5668

square root √‾

求底數，指數是2。

☐ ^ 2 ≡ 7 (mod 9)

移項即是平方根。

√7 ≡ ☐ (mod 9)

根據「歐拉準則」、「二次互反律」，餘數平方根是否有解：a^½的費馬小定理，+1有解，-1無解。

如果模數不是質數，那麼我就不知道該怎麼辦了。

/* x ^ 2 ≡ a (mod m) , m is prime */ bool has_square_root(int a, int m) { if (a == 0 || m <= 2) return true; return pow(a, (p-1)/2, p) == 1; } /* ⎛ a ⎞ ⎧ 0 if x² ≡ a ≡ 0 (mod p) ⎜———⎟ = ⎨ +1 if x² ≡ a (mod p) , p is odd prime ⎝ p ⎠ ⎩ -1 if x² ≢ a (mod p) */ int legendre_symbol(int a, int p) { if (a % p == 0) return 0; return pow(a, (p-1)/2, p) == 1 ? +1 : -1; }

餘數平方根屬於NP-complete問題。

餘數平方根的演算法是「Tonelli–Shanks algorithm」、「Cipolla algorithm」、「Cipolla–Lehmer algorithm」。

如果模數不是質數，那麼我就不知道該怎麼辦了。

UVa 10831 luogu P5491 U124195

演算法（Tonelli–Shanks algorithm）

/* x ^ 2 ≡ a (mod m) , m is prime */ int sqrt(int a, int m) { if (a == 0 || m == 2) return a; int n = (m - 1) / 2; if (pow(a, n, m) != 1) return -1; if (m % 4 == 3) { int x = pow(a, (m+1)/4, m); return (x * 2 <= m) ? x : (m - x); } int b = 1; while (pow(b, n, m) == 1) b++; int i = n, j = 0; while (i % 2 == 0) { i /= 2; j /= 2; int x = mul(pow(a, i, m), pow(b, j, m), m); if (x == m-1) j += n; } i /= 2; j /= 2; int x = mul(pow(a, i+1, m), pow(b, j, m), m); return (x * 2 <= m) ? x : (m - x); }

演算法（Cipolla's algorithm）

struct Complex {int a, b;}; Complex mul(Complex a, Complex b, int w, int m) { return (Complex) { (a.a * b.a + a.b * b.b * w) % m, (a.a * b.b + a.b * b.a) % m // call add(a, b, m) and mul(a, b, m) if needed }; } Complex pow(Complex a, int b, int w, int m) { Complex x = {1, 0}; for (; b > 0; b >>= 1) { if (b & 1) x = mul(x, a, w, m); a = mul(a, a, w, m); } return x; } /* x ^ 2 ≡ a (mod m) , m is prime */ int sqrt(int a, int m) { if (a == 0 || m == 2) return a; int n = (m - 1) / 2; if (pow(a, n, m) != 1) return -1; int r, w; do { r = rand() % m; w = sub(mul(r, r, m), a, m); } while (pow(w, n, m) == 1); Complex x = pow((Complex){r, 1}, n+1, w, m); return (x.a * 2 <= m) ? x.a : (m - x.a); }

演算法（Cipolla–Lehmer algorithm）

http://library.msri.org/books/Book44/files/02buhler.pdf
solve y² ≡ c (mod p)
(1) select random number b such that D = b² - 4c is non-residue
(2) α is a root of (x² - bx + c)
    thus β = α^p is also a root
    thus c = αβ = α^(p+1)
(3) return α^((p+1)/2)

https://arxiv.org/abs/1309.2831
solve y² ≡ c (mod p)
(1) h := (b² - 4c)^((p-1)/2) (mod p)
(2) if h ≡ 0 or 1 (mod p) then s := 0
(3) if h ≡ -1 (mod p) then s := 1
(4) q(x) := x^((p+1)/2) mod (x² - bx + c)
    where q(x) = c₁x + c₀ for integers c₀, c₁
(5) y := s c₀
(6) return y as the output

primitive root【查無數學運算符號】

複數系統的單位根們，藉由乘方與開方，數格子、繞圈圈，可以得到彼此。餘數系統的單位根們，多半不可以。

因此數學家創造新名詞「原根」：

條件一、底數的可能範圍是「與模數互質的所有數字」，總共φ(m)個。這些底數擁有倒數，才可以開方。

條件二、次方值模數規定為φ(m)。等我想一下原因。

條件三、指數的可能範圍是「與次方值模數互質的所有數字」，總共φ(φ(m))個。以這些指數進行乘方與開方，才可以得到彼此。

滿足上述條件的底數，稱作「原根」。由於互質的緣故，原根的每個次方，恰是底數的可能範圍的每個數字。這個性質相當優美，數學家便以此為定義。

一、原根的每個次方，恰好生成所有與模數互質的數字。

二、模數m是2、4、pⁿ、2pⁿ，原根數量是φ(φ(m))個；模數m是其他數字，沒有原根。p是奇質數，n是正整數。

試誤法：窮舉底數。針對一種底數，窮舉指數。

試除法：窮舉底數。針對一種底數，窮舉φ(m)的因數。

質因數分解φ(m)，得到質因數p₁ p₂ ...。
針對一種底數x，窮舉質因數p₁ p₂ ...。
如果x^(φ(m)/p₁) x^(φ(m)/p₂) ...皆非1，x就是原根。
（φ(m)改成λ(m)，檢測次數更少；然而λ(m)更難算。）

/* x ^ φ(m) ≡ 1 (mod m) , x is generator */ bool has_primitive_root(int m) { if (m <= 1) return false; if (m == 2 && m == 4) return true; if (m % 2 == 0) m /= 2; if (m % 2 == 0) return false; // https://mathoverflow.net/questions/106313/ return is_prime_power(m); } bool has_primitive_root(Factor& fac_m) { int N = fac_m.size(); if (N == 0 || N > 2) return false; int& p1 = fac_m[0].first; int& e1 = fac_m[0].second; if (N == 1 && p1 == 2 && e1 > 2) return false; if (N == 2 && !(p1 == 2 && e1 == 1)) return false; return true; } bool is_primitive_root(int x, int m) { int phi_m = phi(m); for (int i=1; i<phi_m; i++) if (pow(x, i, m) == 1) return false; return true; } bool is_primitive_root(int x, int m, int phi_m, Factor& fac_phi_m) { int N = fac_phi_m.size(); for (int i=0; i<N; i++) { int p = fac_phi_m[i].first; if (pow(x, phi_m/p, m) == 1) return false; } return true; } int least_primitive_root(int m, int phi_m, Factor& fac_phi_m) { for (int x=1; x<m; x++) if (gcd(x, m) == 1) if (is_primitive_root(x, m, phi_m, fac_phi_m)) return x; return -1; // 無解 } vector<int> primitive_root(int m) { Factor fac_m = factorize(m); if (!has_primitive_root(fac_m)) return {}; int phi_m = phi(m, fac_m); Factor fac_phi_m = factorize(phi_m); int g = least_primitive_root(m, phi_m, fac_phi_m); if (g == -1) return {}; vector<int> v; for (int i=1, gi=g; i<=phi_m; i++, gi=mul(gi, g, m)) if (gcd(i, phi_m) == 1) v.push_back(gi); // g^i sort(v.begin(), v.end()); return v; }

luogu P6091

餘數開方可以利用原根

4^5與8^3誰比較大？
底數換成一樣，就能比較大小了。
4^5 = (2^2)^5 = 2^10
8^3 = (2^3)^3 = 2^9

x ^ a ≡ b (mod m)   已知a b m，求x。

令模m的其中一個原根是g，作為底數。
令 x = g^p，b = g^q
原式變成 g ^ ap ≡ g ^ q (mod m)
繼而變成 ap ≡ q (mod φ(m))

一、g ^ φ(m) ≡ 1 (mod m) 求g，原根
二、b ≡ g ^ q (mod m)    求q，對數
三、ap ≡ q (mod φ(m))    求p，除法
四、x ≡ g ^ p (mod m)    求x，次方

餘數系統的特色：有限範圍

餘數系統有個非常重要的特性：數字大於等於零、不超過模數。

電腦只能處理有限範圍的數字。餘數系統得以發揮功效。

實數系統的加法表、乘法表
+ | 0  1  2  3 ...   × | 0  1  2  3 ...
--|---------------   --|---------------
0 | 0  1  2  3 ...   0 | 0  0  0  0 ...
1 | 1  2  3  4 ...   1 | 0  1  2  3 ...
2 | 2  3  4  5 ...   2 | 0  2  4  6 ...
3 | 3  4  5  6 ...   3 | 0  3  6  9 ...
: | :  :  :  :       : | :  :  :  :    

餘數系統的加法表、乘法表
(mod 1)  (mod 2)    (mod 3)       (mod 4)          (mod 5)
+ | 0    + | 0  1   + | 0  1  2   + | 0  1  2  3   + | 0  1  2  3  4
--|--    --|-----   --|--------   --|-----------   --|--------------
0 | 0    0 | 0  1   0 | 0  1  2   0 | 0  1  2  3   0 | 0  1  2  3  4
         1 | 1  0   1 | 1  2  0   1 | 1  2  3  0   1 | 1  2  3  4  0
                    2 | 2  0  1   2 | 2  3  0  1   2 | 2  3  4  0  1
                                  3 | 3  0  1  2   3 | 3  4  0  1  2
                                                   4 | 4  0  1  2  3

(mod 1)  (mod 2)    (mod 3)       (mod 4)          (mod 5)
× | 0    × | 0  1   × | 0  1  2   × | 0  1  2  3   × | 0  1  2  3  4
--|--    --|-----   --|--------   --|-----------   --|--------------
0 | 0    0 | 0  0   0 | 0  0  0   0 | 0  0  0  0   0 | 0  0  0  0  0
         1 | 0  1   1 | 0  1  2   1 | 0  1  2  3   1 | 0  1  2  3  4
                    2 | 0  2  1   2 | 0  2  0  2   2 | 0  2  4  1  3
                                  3 | 0  3  2  1   3 | 0  3  1  4  2
                                                   4 | 0  4  3  2  1

連加循環

餘數系統有個非常重要的特性：數字循環出現、甚至全部出現。

不斷連加，導致循環。

畫在圈圈內部，更清楚。

連加畫在圓的等分點上，得以構造正多邊形、正多角星。

連加畫在數線上，得以連結到最小公倍數的概念。

循環節長度等於「最小公倍數除以連加數」，也等於「模數除以最大公因數」。請讀者自行按圖推理。

當模數是連加數的倍數（連加數是模數的因數）（連加數整除模數），大多數情況無法遭遇全部數字，除非連加數、模數是一。

考慮所有情況，歸納簡潔結論：連加數與模數，最大公因數不等於一（不互質），遭遇部分數字；最大公因數等於一（互質），遭遇全部數字。

簡單一句話：互質，遭遇全部數字。

順帶一提，「與模數互質的連加數」總共有φ(m)個。

連乘循環

不斷連乘，導致循環。

加法循環，跳躍很規律；一種連加數，只有一種循環節。

乘法循環，跳躍沒規律；一種連乘數，擁有各種循環節。

想要確認循環節起點、循環節長度，可以使用Floyd's algorithm或Brent's algorithm。

乘法群

數學家傾向討論性質優美的事物。

首先區隔「與模數互質的數字」和「不與模數互質的數字」，只取前者。

「與模數互質的數字」不斷相乘，絕不會得到「不與模數互質的數字」，而且所有數字都位於某個循環節之內。

由於與模數互質，每個數字都只有唯一一個倒數，餘數除法亦成立！乘法正向跳躍，除法反向跳躍，雙向都通。

「與模數互質的數字」暨乘法除法，性質優美，自成一格，數學家稱作「乘法群」。一種模數得到一種乘法群。

順帶一提，「與模數互質的數字」總共有φ(m)個。

次方循環

連乘循環的特例。起點是零次方。

循環長度必定是λ(m)的因數、或者是φ(m)的某些因數。求得確切因數，目前沒有快速演算法，只能使用試誤法。

原根

首先取出「與模數互質的數字」當作底數。引入乘法群的觀點，這些底數的任意次方，仍是「與模數互質的數字」。

從中取出「遭遇所有與模數互質的數字」的底數。模數是2、4、pⁿ、2pⁿ才有可能。p是大於2的質數，n是正整數。

求得原根，目前沒有快速演算法，只能使用試誤法。但是只要求得其中一個原根，就容易求得所有原根。手法是連加循環！

每種次方剛好遭遇每種數字。依照遭遇順序，重新串成一圈。

以原根的某個次方（某個次方連加數），嘗試當作新的原根。只有「與次方值模數互質的次方數」才是合適的次方數。

再來一個例子。

模數13，互質數字1 2 ... 12，總共φ(13) = 12個。

試誤法求得其中一個原根2，上述互質數字依照原根2的次方順序重新串成一圈，2⁰ ... 2¹¹。

次方模數φ(13) = 12，互質數字1 5 7 11，總共φ(φ(13)) = 4個，當作次方連加數。

次方連加數1，得到原根2¹。次方連加數5，得到原根2⁵。次方連加數7，得到原根2⁷。次方連加數11，得到原根2¹¹。

2¹ 2⁵ 2⁷ 2¹¹分別等於2 6 11 7。得到模數13的所有原根。

polynomial ∑i=0n-1cᵢxⁱ

模數相同時，餘數們可以構成餘數多項式。

x³ + 2x² - 5x + 1 (mod 3)

係數通常是寫最接近零、大於等於零的那一個。

x³ + 2x² - 5x + 1 ≡ x³ + 2x² + x + 1 (mod 3)

factorization n = ∏k=1ω(n)pₖ^eₖ

整數：列舉質數、判斷質數、質因數分解、最大公因數。

列舉質數：2, 3, 5, 7, 11, ...
判斷質數：97 is a prime number
質因數分解：999 = 3 × 3 x 3 x 37
最大公因數：gcd(104, 112, 116) = 4

餘數：不存在質數的概念。即便是餘數1也可以乘法分解。

列舉質數：2 (mod 8), 3 (mod 8), ...  ✘
判斷質數：97 (mod 8) is a prime number ✘
質因數分解：999 ≡ 3 × 3 x 3 x 37 (mod 8) ✘
最大公因數：gcd(104, 112, 116) ≡ 4 (mod 8) ✘

polynomial factorization f(x) = ∏i=0deg(f)(x - aᵢ)

整數多項式：列舉質式、判斷質式、因式分解、最大公因式。

列舉質式：x, x + 1, x + 2, ...
判斷質式：x² + x + 1 is an irreducible polynomial
因式分解：2x² + 5x + 2 = (2x + 1)(x + 2)
最大公因式：gcd(x² - 4x + 4, x² - x - 2) = x - 2

餘數多項式：存在質式的概念。乘法分解受到次方的限制。

列舉質式：x (mod 2), x + 1 (mod 2), x² + x + 1 (mod 2), ...
判斷質式：x³ + x + 1 (mod 2) is an irreducible polynomial
因式分解：x² + 1 (mod 2) ≡ x + 1 (mod 2) × x + 1 (mod 2)
最大公因式：gcd(x³ + 1 (mod 2), x² + 1 (mod 2)) ≡ x + 1 (mod 2)

polynomial congruence f(x) ≡ b (mod m)

模數相同時，餘數們可以構成餘數方程式（等式）：左右兩式同餘（相等）。

x² - 2x + 1 ≡ 3x² + x + 1 (mod 5)

餘數方程式求解，化作餘數方程式求根。

x³ + 2x² - 5x + 1 ≡ 0 (mod 3)

簡單的演算法是試誤法：窮舉答案，代入計算。

x ≡ 1 (mod 3)

當模數是質數，根據「polynomial remainder theorem」與「Lagrange's theorem」，N-1次餘數多項式方程式頂多N種解。

當模數是質數，大家習慣視作finite field的特例。演算法是有限體多項式分解「Cantor–Zassenhaus algorithm」的簡化。【尚待確認】

Cantor–Zassenhaus(f)
{
	f = gcd(f, x^p - x)
	if (deg(f) == 1) return root(f)
	while (true)
	{
		b = random()
		g = gcd(f, (x+b)^((p-1)/2) - 1)
		if (0 < deg(g) < deg(f)) return CZ(g) ∪ CZ(f/g)
	}
}

Hensel lifting將模數從質數拓展至質數次方。

given f(a) ≡ 0 (mod pⁿ)
find f(aꜛ) ≡ 0 (mod p²ⁿ)
assume aꜛ ≡ a (mod pⁿ)
f(aꜛ) ≡ f(a)(aꜛ-a)⁰ + f′(a)(aꜛ-a)¹ + f″(a)(aꜛ-a)²/2! + ... (mod p²ⁿ)
f(aꜛ) ≡ f(a) + f′(a)(aꜛ-a) (mod p²ⁿ)      ^^^^^^^ double the zeros
aꜛ ≡ a - f(a)​ / f′(a) (mod p²ⁿ)
aꜛ ≡ a - f(a)​ / f′(a) (mod pⁿ⁺¹)   weak version

中國餘數定理將模數從質數次方拓展至任意數。

{ x ≡ a₁ (mod p₁e₁)
{ x ≡ a₂ (mod p₂e₂)  ←—→  x ≡ a (mod p₁e₁ × p₂e₂ × ...)
{ :   :       :

至此解決了任意模數的餘數多項式方程式求解。

linear congruences Ax⃗ ≡ b⃗ (mod m)

餘數一次方程組，模數皆相同。

{  x - 2y + 1z ≡ 1 (mod m)
{ 3x + 2y + 1z ≡ 2 (mod m)
{  x + 2y + 3z ≡ 3 (mod m)

沿用實數一次方程組的演算法，實數運算改成餘數運算。

luogu P4783

system of congruences F(x⃗) ≡ y⃗ (mod m⃗)

許多道方程式同時成立。

{  x² - 2x + 1 ≡ x + 1  (mod 3)
{ 3x² + 2x + 1 ≡ x - 1  (mod 5)
{  x² + 2x + 3 ≡ x² + 1 (mod 7)

我不會解！

pendulum snake

faro shuffle

water jug problem

手邊有兩個容器，一個三公升、一個五公升，都沒有刻度。另外身邊還有一個水龍頭和一個水槽，我們可以用水龍頭的水裝滿容器，也可以把容器的水倒入水槽（有點浪費），或者把一個容器的水倒入到另一容器、裝滿另一容器。如何利用這兩個容器量出四公升的水？

演算法（state space search）

請參考「3 jugs problem」。

BFS tree恰好是水量變化最少的路線。可用下面的模型證明。

UVa 571

演算法（modeling）

以三角座標系統當作模型：

首先建立二維座標系，只有第一象限。其中一軸為三公升的容器，範圍是零到三；另外一軸為五公升的容器，範圍是零到五。然後畫上很多斜線：

座標代表著兩容器的水量。我們描一個點來表示目前兩容器的水量。一開始起點在原點，代表著兩個容器都沒有裝水：

如果三公升的容器填滿水或倒光水，點就往三公升軸的一端或另一端移動到底；五公升的容器亦同。如果兩個容器互相倒水，點就往斜線方向移動到底：

至此，water jug problem變成了：由原點畫線，只能畫直線、橫線、斜線並畫到底，然後畫到座標其中一個維度的數值是四的地方。

演算法（modeling）

以餘數方程式當作模型：

兩容器，體積a和b；量水，體積c。變成ax ≡ c (mod b)。

ICPC 6501

Josephus problem

有n個人圍成一圈，現在從第一個人開始報數，數到第m人時，就殺掉這第m人；然後從被殺的下一位繼續重新報數，數到第m人時，就殺掉這第m人。如此不斷數m人、殺此人，直到最後會剩下一個人，請問他是誰？

這個美式風格的問題似乎有點殘酷。如果改成「不斷數m個人，被點名的人就臉頰泛紅，害羞的跑開了」這樣應該會童真一點。

演算法（simulation）

直接模擬「不斷數m個人，被點名的人就臉頰泛紅，害羞的跑開了」這個行為。時間複雜度O(nm)。

有個加速的小手段是：當要數的人數超過實際人數時，可以模一下、取餘數。

bool live[100]; // 記錄哪些人是活人 // 找出下一個活人 int next(int& a, int n) { do a = (a + 1) % n; while (!live[a]); } void josephus(int n, int m) { // 一開始所有人都活著 for (int i=0; i<n; ++i) live[i] = true; int answer = 0; // 開始數的地方 for (int man = n; man > 1; --man) { // 數 m-1 個人（第一個人剛剛數過了） // for (int i=0; i<m-1; ++i) next(answer, n); for (int i=0; i<(m-1)%man; ++i) next(answer, n); // 第 m 個人害羞的跑開了 live[answer] = false; // 找到下一個人，重新報數 next(answer, n); } cout << "存活的人是" << answer << "號"; }

UVa 133 305 402

演算法（modeling）

數人和殺人的動作可以整合成queue的操作。首先把每個人依序塞入queue，然後輪流地pop和push m-1人，於pop第m人時，不要將他塞回queue裡面，這樣就成功的模擬了！時間複雜度O(nm)。實作時可以使用circular queue節省記憶體空間。

void josephus(int n, int m) { // 將 n 個人塞入 queue queue<int> q; for (int i=0; i<n; ++i) q.push(i); int answer; while (!q.empty()) { // pop 和 push m-1 人 for (int i=0; i<m-1; ++i) { int a = q.front(); q.pop(); q.push(a); } // 第 m 個人 pop 出來後就不塞回去 answer = q.front(); q.pop(); } cout << "存活的人是" << answer << "號"; }

演算法（dynamic programming）

除去一人之後，剩下來的人重新編號，就變成了子問題了。觀察原編號和新編號的關係，得到一遞迴公式：

f(n, m) = (f(n-1, m) + m) % n
f(1, m) = 0;

f(n, m)：最後活下來的人的編號。

用此遞迴公式進行計算，時間複雜度O(n)。

// bottom-up dynamic programming void josephus(int n, int m) { int answer = 0; for (int i=1; i<=n; ++i) answer = (answer + m) % i; cout << "存活的人是" << answer << "號"; }

UVa 10015 151 440 10940 11351 180

演算法