convolution

「卷積」。級數乘法。

大家主要討論兩種級數：冪級數（多項式）、狄利克雷級數。

一、加性卷積（柯西乘積）＝冪級數乘法（多項式乘法）。

(2 -5  1)        ←—→  2x⁰ - 5x¹ + 1x²
    ∗                        ×
(1 -1  0)        ←—→  1x⁰ - 1x¹ + 0x²
    ‖                        ‖
(2 -7  7  1  0)  ←—→  2x⁰ - 7x¹ + 7x² + 1x³ + 0x⁴

convolution           power series multiplication
(Cauchy product)

二、乘性卷積（狄利克雷乘積）＝狄利克雷級數乘法。

(2 -5  1)        ←—→  2⋅1ˣ - 5⋅2ˣ + 1⋅3ˣ
    ∗                        ×
(1 -1  0)        ←—→  1⋅1ˣ - 1⋅2ˣ + 0⋅3ˣ
    ‖                        ‖
(2 -7  1  5  0   ←—→  2⋅1ˣ - 7⋅2ˣ + 1⋅3ˣ + 5⋅4ˣ + 0⋅5ˣ
 -1  0  0  0)       - 1⋅6ˣ + 0⋅7ˣ + 0⋅8ˣ + 0⋅9ˣ

convolution           Dirichlet series multiplication
(Dirichlet product)

circular convolution

「循環卷積」。數列頭尾循環。（當xⁿ循環、當nˣ循環）

整數系統、實數系統不可能出現循環卷積。餘數系統、複數系統才可能出現循環卷積。

(2 -5  1)  ←—→  2x⁰ - 5x¹ + 1x²
    ⊛                  ⊗
(1 -1  0)  ←—→  1x⁰ - 1x¹ + 0x²    (when x³ = x⁰, x⁴ = x¹, ...)
    ‖                  ‖
(3 -7  7)  ←—→  3x⁰ - 7x¹ + 7x²

circular        power series circular multiplication
convolution

(2 -5  1)  ←—→  2⋅1ˣ - 5⋅2ˣ + 1⋅3ˣ
    ⊛                  ⊗
(1 -1  0)  ←—→  1⋅1ˣ - 1⋅2ˣ + 0⋅3ˣ   (when 4ˣ = 1ˣ, 5ˣ = 2ˣ, ...)
    ‖                  ‖
(7 -7  0)  ←—→  7⋅1ˣ - 7⋅2ˣ + 0⋅3ˣ

circular        Dirichlet series circular multiplication
convolution

convolution兩種觀點

級數有兩種觀點：多項式觀點、矩陣觀點。

卷積也有這兩種觀點。

(a₀ a₁ a₂ a₃ a₄) ∗ (b₀ b₁ b₂) = (c₀ c₁ c₂ c₃ c₄ c₅ c₆)

一、多項式觀點。

  (a₀x⁰ + a₁x¹ + a₂x² + a₃x³ + a₄x⁴) × (b₀x⁰ + b₁x¹ + b₂x²)
= (c₀x⁰ + c₁x¹ + c₂x² + c₃x³ + c₄x⁴ + c₅x⁵ + c₆x⁶)

二、矩陣觀點。

⎡ a₀ 0  0  ⎤          ⎡ c₀ ⎤     c₀ = a₀b₀
⎢ a₁ a₀ 0  ⎥          ⎢ c₁ ⎥     c₁ = a₀b₁ + a₁b₀
⎢ a₂ a₁ a₀ ⎥ ⎡ b₀ ⎤   ⎢ c₂ ⎥     c₂ = a₀b₂ + a₁b₁ + a₂b₀
⎢ a₃ a₂ a₁ ⎥ ⎢ b₁ ⎥ = ⎢ c₃ ⎥     c₃ = a₁b₂ + a₂b₁ + a₃b₀
⎢ a₄ a₃ a₂ ⎥ ⎣ b₂ ⎦   ⎢ c₄ ⎥     c₄ = a₂b₂ + a₃b₁ + a₄b₀
⎢ 0  a₄ a₃ ⎥          ⎢ c₅ ⎥     c₅ = a₃b₂ + a₄b₁
⎣ 0  0  a₄ ⎦          ⎣ c₆ ⎦     c₆ = a₄b₂

convolution兩種觀點

矩陣有兩種觀點：矩陣切成直條（向量們的加權總和）、矩陣切成橫條（許多次向量點積）。請見本站文件「basis」。

卷積也有這兩種觀點。

(a₀ a₁ a₂ a₃ a₄) ∗ (b₀ b₁ b₂) = (c₀ c₁ c₂ c₃ c₄ c₅ c₆)

一、矩陣切成直條：數列移位、數列加權總和。

此觀點出現於「signal interpolation」。

(c₀ c₁ c₂ c₃ c₄ c₅ c₆) = b₀ ⋅ (a₀ a₁ a₂ a₃ a₄ 0  0 )
                       + b₁ ⋅ (0  a₀ a₁ a₂ a₃ a₄ 0 )
                       + b₂ ⋅ (0  0  a₀ a₁ a₂ a₃ a₄)

二、矩陣切成橫條：數列顛倒、數列移位、數列點積。

此觀點出現於「filter」、「image filtering」。

c₀ = (a₀ 0  0 ) ∙ (b₀ b₁ b₂)
c₁ = (a₁ a₀ 0 ) ∙ (b₀ b₁ b₂)
c₂ = (a₂ a₁ a₀) ∙ (b₀ b₁ b₂)
c₃ = (a₃ a₂ a₁) ∙ (b₀ b₁ b₂)
c₄ = (a₄ a₃ a₂) ∙ (b₀ b₁ b₂)
c₅ = (0  a₄ a₃) ∙ (b₀ b₁ b₂)
c₆ = (0  0  a₄) ∙ (b₀ b₁ b₂)

奧義

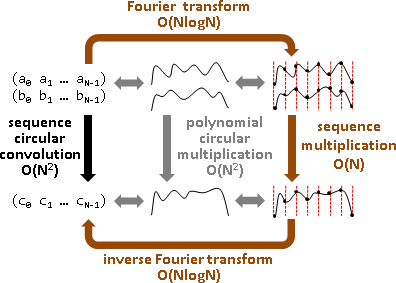
多項式乘法，時間複雜度O(N²)，可以降為O(NlogN)。

取巧方式：多項式多點求值、函數值乘法、多項式內插。

多項式多點求值，x值是特殊數值：N次單位根的倒數，形成傅立葉轉換。多項式內插，則形成逆向傅立葉轉換。

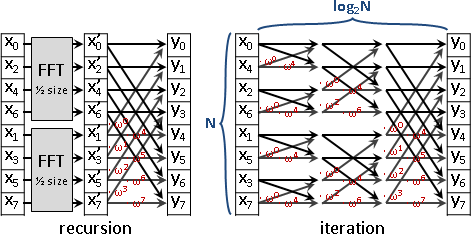
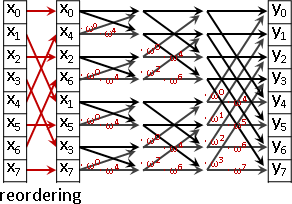
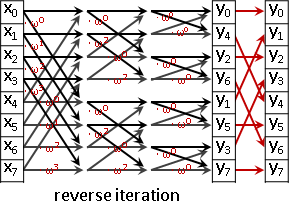
傅立葉轉換擁有高速演算法，時間複雜度O(NlogN)。

數列函數轉換【尚無正式名稱，也許是generating function】

一、數列＝多項式。

(a₀ a₁ a₂)  ←—→  a₀x⁰ + a₁x¹ + a₂x²

二、數列加法＝多項式加法。

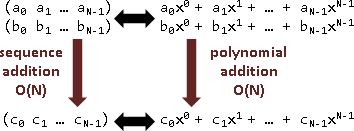
(a₀ a₁ a₂) + (b₀ b₁ b₂) = (a₀+b₀ a₁+b₁ a₂+b₂)

        a₀ x⁰ +       a₁ x¹ +       a₂ x²
+)      b₀ x⁰ +       b₁ x¹ +       b₂ x²
—————————————————————————————————————————
   (a₀+b₀) x⁰ +  (a₁+b₁) x¹ +  (a₂+b₂) x²

三、數列卷積＝多項式乘法。

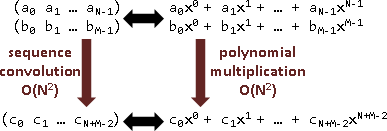
(a₀ a₁ a₂) ∗ (b₀ b₁ b₂) = (c₀ c₁ c₂ c₃ c₄)

c₀ = a₀b₀
c₁ = a₀b₁ + a₁b₀
c₂ = a₀b₂ + a₁b₁ + a₂b₀
c₃ = a₁b₂ + a₂b₁
c₄ = a₂b₂

                         a₀ x⁰ +   a₁ x¹ +   a₂ x²
×)                       b₀ x⁰ +   b₁ x¹ +   b₂ x²
——————————————————————————————————————————————————
                       a₀b₂ x² + a₁b₂ x³ + a₂b₂ x⁴
             a₀b₁ x¹ + a₁b₁ x² + a₂b₁ x³
   a₀b₀ x⁰ + a₁b₀ x¹ + a₂b₀ x²
——————————————————————————————————————————————————
     c₀ x⁰ +   c₁ x¹ +   c₂ x² +   c₃ x³ +   c₄ x⁴

四、數列循環卷積＝多項式循環乘法。（當xⁿ循環）

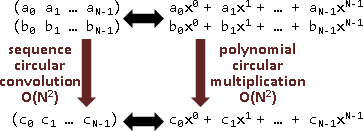
(a₀ a₁ a₂) ⊛ (b₀ b₁ b₂) = (c₀ c₁ c₂)

c₀ = a₁b₂ + a₂b₁ + a₀b₀
c₁ = a₂b₂ + a₀b₁ + a₁b₀
c₂ = a₀b₂ + a₁b₁ + a₂b₀

                         a₀ x⁰ +   a₁ x¹ +   a₂ x²
⊗)                       b₀ x⁰ +   b₁ x¹ +   b₂ x²
—————————————————————————————————————————————————————
                       a₀b₂ x² + a₁b₂ x³ + a₂b₂ x⁴
             a₀b₁ x¹ + a₁b₁ x² + a₂b₁ x³
   a₀b₀ x⁰ + a₁b₀ x¹ + a₂b₀ x²
—————————————————————————————————————————————————————
   a₁b₂ x⁰ + a₂b₂ x¹ + a₀b₂ x²   (when x³ = x⁰, x⁴ = x¹, ...)
   a₂b₁ x⁰ + a₀b₁ x¹ + a₁b₁ x²
   a₀b₀ x⁰ + a₁b₀ x¹ + a₂b₀ x²
—————————————————————————————————————————————————————
     c₀ x⁰ +   c₁ x¹ +   c₂ x²

係值轉換【尚無正式名稱，也許是evaluation isomorphism】

一、N-1次多項式，N個係數變成N個函數值。

冪級數恰是多項式函數。藉由多項式內插，N個函數值可以還原成N個係數。請見本站文件「polynomial interpolation」。

             a₀x⁰ + a₁x¹ + a₂x²
(a₀ a₁ a₂)  <——————————————————>  (y₀ y₁ y₂)
                 (x₀ x₁ x₂)

二、係數加法＝多項式加法＝函數值加法。

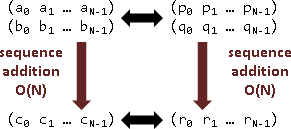
             a₀x⁰ + a₁x¹ + a₂x²
(a₀ a₁ a₂)  <——————————————————>  (p₀ p₁ p₂)
    +        b₀x⁰ + b₁x¹ + b₂x²       +
(b₀ b₁ b₂)  <——————————————————>  (q₀ q₁ q₂)
    ‖        c₀x⁰ + c₁x¹ + c₂x²       ‖
(c₀ c₁ c₂)  <——————————————————>  (r₀ r₁ r₂)
                 (x₀ x₁ x₂)

三、係數卷積＝多項式乘法＝函數值乘法。

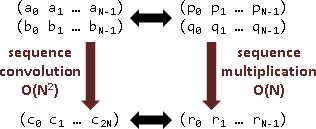
                   a₀x⁰ + a₁x¹ + a₂x²
(a₀ a₁ a₂)        <————————————————————————————————>  (p₀ p₁ p₂)
    ∗              b₀x⁰ + b₁x¹ + b₂x²                     ×
(b₀ b₁ b₂)        <————————————————————————————————>  (q₀ q₁ q₂)
    ‖              c₀x⁰ + c₁x¹ + c₂x² + c₃x³ + c₄x⁴       ‖
(c₀ c₁ c₂ c₃ c₄)  <————————————————————————————————>  (r₀ r₁ r₂)
                              (x₀ x₁ x₂)

四、係數循環卷積＝多項式循環乘法＝函數值乘法。（當xⁿ循環）

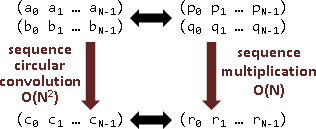
             a₀x⁰ + a₁x¹ + a₂x²
(a₀ a₁ a₂)  <——————————————————>  (p₀ p₁ p₂)
    ⊛        b₀x⁰ + b₁x¹ + b₂x²       ×
(b₀ b₁ b₂)  <——————————————————>  (q₀ q₁ q₂)   (when x³ = x⁰, x⁴ = x¹, ...)
    ‖        c₀x⁰ + c₁x¹ + c₂x²       ‖
(c₀ c₁ c₂)  <——————————————————>  (r₀ r₁ r₂)
                 (x₀ x₁ x₂)

係值轉換（矩陣觀點）【尚無正式名稱】

一、係值轉換視作線性函數、寫作矩陣。

A = [ x⁰ x¹ x² ]   transform

    ⎡ a₀ ⎤
a = ⎢ a₁ ⎥         coefficients
    ⎣ a₂ ⎦

                  ⎡ a₀ ⎤
Aa = [ x⁰ x¹ x² ] ⎢ a₁ ⎥ = a₀x⁰ + a₁x¹ + a₂x²   function value
                  ⎣ a₂ ⎦

二、輸入加法＝輸出加法。

A = [ x⁰ x¹ x² ]

    ⎡ a₀ ⎤       ⎡ b₀ ⎤
a = ⎢ a₁ ⎥   b = ⎢ b₁ ⎥
    ⎣ a₂ ⎦       ⎣ b₂ ⎦

A(a + b) = (Aa) + (Ab)

三、輸入卷積＝輸出乘法。（尺寸不符，需要補項。）

à = [ x⁰ x¹ x² | x³ x⁴ ]

    ⎡ a₀ ⎤       ⎡ b₀ ⎤       ⎡ c₀ ⎤
ã = ⎢ a₁ ⎥   b̃ = ⎢ b₁ ⎥   c̃ = ⎢ c₁ ⎥
    ⎢ a₂ ⎥       ⎢ b₂ ⎥       ⎢ c₂ ⎥
    ⎢————⎥       ⎢————⎥       ⎢————⎥
    ⎢ 0  ⎥       ⎢ 0  ⎥       ⎢ c₃ ⎥
    ⎣ 0  ⎦       ⎣ 0  ⎦       ⎣ c₄ ⎦

Ã(ã ∗ b̃) = (Ãã) × (Ãb̃)

四、輸入循環卷積＝輸出乘法。

A = [ x⁰ x¹ x² ]

    ⎡ a₀ ⎤       ⎡ b₀ ⎤
a = ⎢ a₁ ⎥   b = ⎢ b₁ ⎥
    ⎣ a₂ ⎦       ⎣ b₂ ⎦

A(a ⊛ b) = (Aa) × (Ab)

指數一齊添上任意倍率，運算性質仍成立。

元素一齊添上任意倍率，運算性質仍成立。

一個橫條併成多個橫條，運算性質仍成立。

A = [ x⁰ x¹ x² ]
A = [ x⁰ x⁵ x¹⁰ ]
A = [ x⁰ x⁻⁷ x⁻²¹ ]
A = [ x⁰ x⁰ x⁰ ]  

A = [ x⁰ x¹ x² ]
A = [ 7x⁰ 7x¹ 7x² ]
A = [ -x⁰ -x⁵ -x¹⁰ ]
A = [ 0 0 0 ]

    ⎡ 7x⁰ 7x¹  7x²   ⎤
A = ⎢ -x⁰ -x⁵  -x¹⁰  ⎥
    ⎢  x⁰  x⁻⁷  x⁻²¹ ⎥
    ⎣  x⁰  x⁰   x⁰   ⎦

對偶係值轉換（矩陣觀點）【尚無正式名稱】

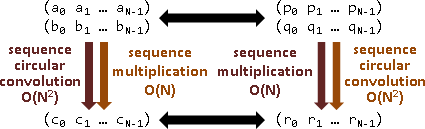
接下來繼續補強矩陣，既滿足「輸入循環卷積＝輸出乘法」，也滿足「輸入乘法＝輸出循環卷積」，形成對偶運算。

從數學來看，補強性質，達成了對稱之美。從計算學來看，追加限制，產生了特殊演算法。

令原矩陣A、反矩陣A⁻¹，同時具備運算性質。一種嘗試是正規正交矩陣A⁻¹ = Aᵀ。

實數系統，xⁿ漸增，數值漸增，無法正規正交。失敗！

               ⎡ x⁰ x⁰ x⁰ x⁰ .. ⎤
               ⎢ x⁰ x¹ x² x³ .. ⎥
A = A⁻¹ = Aᵀ = ⎢ x⁰ x² x⁴ x⁶ .. ⎥  ✘
               ⎢ x⁰ x³ x⁶ x⁹ .. ⎥
               ⎣ :  :  :  :     ⎦

進一步嘗試封閉循環：令xⁿ循環。

一、複數系統傅立葉轉換：令x是N次單位根（的倒數）。

二、餘數系統數論轉換：令x是N階單位根（的倒數）。

Fourier transform: x = e-𝑖(2π/N), Nth root of unity
number theoretic transform: x = root of unity with order N

    ⎡ x⁰ x⁰ x⁰ x⁰ .. ⎤             ⎡ x⁻⁰ x⁻⁰ x⁻⁰ x⁻⁰ .. ⎤
    ⎢ x⁰ x¹ x² x³ .. ⎥          1  ⎢ x⁻⁰ x⁻¹ x⁻² x⁻³ .. ⎥
A = ⎢ x⁰ x² x⁴ x⁶ .. ⎥   A⁻¹ = ——— ⎢ x⁻⁰ x⁻² x⁻⁴ x⁻⁶ .. ⎥
    ⎢ x⁰ x³ x⁶ x⁹ .. ⎥          N  ⎢ x⁻⁰ x⁻³ x⁻⁶ x⁻⁹ .. ⎥
    ⎣ :  :  :  :     ⎦             ⎣ :   :   :   :      ⎦

總結：傅立葉轉換

數列、函數，互相轉換！

正向轉換：頭腦體操O(1)。

反向轉換：頭腦體操O(1)。

(a₀ a₁ a₂)  ←—→  a₀x⁰ + a₁x¹ + a₂x²

係數、函數值，互相轉換！

正向轉換：多項式求值N回合O(N²)。

反向轉換：多項式內插O(N³)。

             a₀x⁰ + a₁x¹ + a₂x²
(a₀ a₁ a₂)  <——————————————————>  (y₀ y₁ y₂)
                 (x₀ x₁ x₂)

矩陣觀點。Vandermonde matrix。

正向轉換：矩陣求值O(N²)。

反向轉換：矩陣求解O(N³)。

⎡ x₀⁰ x₀¹ x₀² ⎤ ⎡ a₀ ⎤   ⎡ y₀ ⎤
⎢ x₁⁰ x₁¹ x₁² ⎥ ⎢ a₁ ⎥ = ⎢ y₁ ⎥
⎣ x₂⁰ x₂¹ x₂² ⎦ ⎣ a₂ ⎦   ⎣ y₂ ⎦

高速演算法：複數系統傅立葉轉換、餘數系統數論轉換。

令矩陣共軛對稱、令矩陣正規正交、令xᵢ是單位根的每種次方、令矩陣邊長是2的次方。

正向轉換：O(NlogN)。

反向轉換：O(NlogN)。

⎡ x₀⁰ x₀¹ x₀² x₀³ ⎤ ⎡ a₀ ⎤   ⎡ y₀ ⎤
⎢ x₁⁰ x₁¹ x₁² x₁³ ⎥ ⎢ a₁ ⎥ = ⎢ y₁ ⎥
⎢ x₂⁰ x₂¹ x₂² x₂³ ⎥ ⎢ a₂ ⎥   ⎢ y₂ ⎥
⎣ x₃⁰ x₃¹ x₃² x₃³ ⎦ ⎣ a₃ ⎦   ⎣ y₃ ⎦

x = (ω⁰ ω¹ ... ωᴺ⁻¹)
ω = root of unity with order N

總結：循環卷積

係值轉換：係數循環卷積＝函數值乘法。

傅立葉轉換：係數循環卷積＝函數值乘法。係數乘法＝函數值循環卷積。

循環卷積演算法：係數循環卷積＝正向傅立葉轉換＆函數值乘法＆逆向傅立葉轉換。

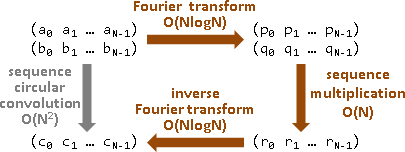
circular convolution演算法
polynomial circular multiplication演算法

數列循環卷積的高速演算法：O(NlogN)！

正向傅立葉轉換O(NlogN)，對應項相乘O(N)，逆向傅立葉轉換O(NlogN)。總時間複雜度O(NlogN)。

傅立葉轉換的弱點是記憶體變兩倍（複數）、浮點數誤差。數論轉換的弱點是數值只能是整數、大於等於零、小於模數。

數列長度必須是2的次方。當數列長度不是2的次方，千萬不能直接補零到2的次方。

循環卷積計算結果：
(a₀ a₁ a₂) ⊛ (b₀ b₁ b₂) = (c₀ c₁ c₂)

c₀ = a₀b₀ + a₁b₂ + a₂b₁
c₁ = a₀b₁ + a₁b₀ + a₂b₂
c₂ = a₀b₂ + a₁b₁ + a₂b₀

補零直到長度是2的次方，計算結果完全不對：
(a₀ a₁ a₂ 0) ⊛ (b₀ b₁ b₂ 0) = (d₀ d₁ d₂ d₃)

d₀ = a₀b₀ + a₂b₂
d₁ = a₀b₁ + a₁b₀
d₂ = a₀b₂ + a₁b₁ + a₂b₀
d₃ = a₁b₂ + a₂b₁

正確方式：先補零直到不受循環影響，再補零直到長度是2的次方，最後讓輸出數列循環。

想要計算
(a₀ a₁ a₂) ⊛ (b₀ b₁ b₂) = (c₀ c₁ c₂)
先補零直到不受循環影響
(a₀ a₁ a₂ 0 0) ⊛ (b₀ b₁ b₂ 0 0) = (d₀ d₁ d₂ d₃ d₄)
再補零直到長度是2的次方
(a₀ a₁ a₂ 0 0 0 0 0) ⊛ (b₀ b₁ b₂ 0 0 0 0 0) = (d₀ d₁ d₂ d₃ d₄ 0 0 0)
最後讓輸出數列循環
c₀ = d₀ + d₃
c₁ = d₁ + d₄
c₂ = d₂

convolution演算法
polynomial multiplication演算法

運用循環卷積，計算卷積。總時間複雜度O(NlogN)。

想要計算
(a₀ a₁ a₂ a₃) ∗ (b₀ b₁ b₂) = (c₀ c₁ c₂ c₃ c₄ c₅)
先補零直到不受循環影響
(a₀ a₁ a₂ a₃ 0 0) ⊛ (b₀ b₁ b₂ 0 0 0) = (c₀ c₁ c₂ c₃ c₄ c₅)
再補零直到長度是2的次方
(a₀ a₁ a₂ a₃ 0 0 0 0) ⊛ (b₀ b₁ b₂ 0 0 0 0 0) = (c₀ c₁ c₂ c₃ c₄ c₅ 0 0)
截斷輸出數列至正確長度
(c₀ c₁ c₂ c₃ c₄ c₅ 0 0) → (c₀ c₁ c₂ c₃ c₄ c₅)

這個說法有點拗口。比較簡單的說法：兩個多項式相乘，則度數相加。為了讓多項式內插能夠得到正解，點數必須等於度數相加。多項式預先補零、追加度數、補足點數。

範例：大數乘法

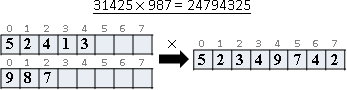
大數乘法即是多項式乘法！

數論轉換、傅立葉轉換得以計算大數乘法，時間複雜度從O(N²)降為O(NlogN)。

char s1[300], s2[300]; int x1[1024], x2[1024], a[1024]; void s2a(char* s, int* a, int n, int N) { int i = 0; for (; i<n; ++i) a[i] = s[n-i-1] - '0'; for (; i<N; ++i) a[i] = 0; } void a2s(int* a, int n) { while (n > 0 && a[n] <= 0) n--; while (n >= 0) cout << a[n--]; cout << '\n'; } void mul(char* s1, char* s2) { int n1 = strlen(s1); int n2 = strlen(s2); // int N = bit_ceil((unsigned int)(n1+n2)); // int N = 1 << (32 - __builtin_clz(n1+n2)); int N = 1; while (N < n1 + n2) N <<= 1; s2a(s1, x1, n1, N); s2a(s2, x2, n2, N); ntt(x1, N, true); ntt(x2, N, true); for (int i=0; i<N; ++i) a[i] = x1[i] * x2[i]; ntt(a, N, false); int n = n1 + n2 - 1; for (int i=0; i<n-1; ++i) { a[i+1] += a[i] / 10; a[i] %= 10; } a2s(a, n); }

範例：兩兩和（Minkowski sum）（X+Y problem）

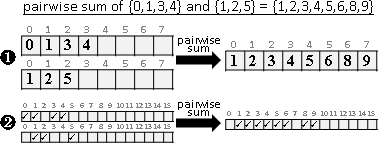
甲集合、乙集合，只有整數。甲取一個數，乙取一個數，相加，會是哪些數？

集合資料結構是循序儲存：窮舉。O(N²)。

集合資料結構是索引儲存：卷積。O(RlogR)。R為數字範圍。

多項式觀點：整數是指數，該整數出現與否（未出現0，出現>0）是係數，兩兩和是多項式乘法。

卷積觀點：整數是索引值，相加是索引值位移，兩兩和是卷積。

範例：組合計數（combination counting）

蓮霧2顆、椪柑3顆、芭樂5顆。欲在盤中擺放6顆水果，有幾種方式？

(x⁰+x¹+x²)(x⁰+x¹+x²+x³)(x⁰+x¹+x²+x³+x⁴+x⁵)，找到x⁶的係數。加是或、乘是且、次方是數量、係數是方式。如同兩兩和。

範例：數列搜尋（sequence searching）

經典問題「一條陣列，尋找一個值」，解法是循序搜尋、排序之後再二元搜尋。

進階問題「一條陣列，尋找一串連續數列」，解法是字串搜尋、卷積。此處討論卷積。

兩串數列 a b
a = (1 2 3 4)
b = (1 3 5 7)

定義兩串數列 a b 的差距：對應項的差的平方的總和。
(1 - 1)² + (2 - 3)² + (3 - 5)² + (4 - 7)²

定義兩串數列 a b 的差距：對應項的差的平方的總和。
sum (a[i] - b[i])²

當差距等於零，則兩串數列相同。
sum (a[i] - b[i])² = 0  ---->  a = b

展開之後，重新整理，以數列為主角：數列每項平方和、數列點積。
  sum (a[i] - b[i])²
= sum (a[i]² + b[i]² - 2 a[i] b[i])
= sum a[i]² + sum b[i]² - 2 sum a[i] b[i]

縮寫。
(a - b)² = a² + b² - 2 (a ∙ b)

兩串數列
(1 2 3 4 5 6)
(3 4 5)

窮舉各種對齊方式，判斷是否相符。
(1 2 3 4 5 6)  (1 2 3 4 5 6)  (1 2 3 4 5 6)  (1 2 3 4 5 6)
 | | |            | | |            | | |            | | |
(3 4 5)          (3 4 5)          (3 4 5)          (3 4 5)

換句話說，判斷差距是否等於零。
        (a - b)²              a²         b²     2(a∙b)
(1-3)² + (2-4)² + (3-5)² = 1²+2²+3² + 3²+4²+5² - 2×26 = 12
(2-3)² + (3-4)² + (4-5)² = 2²+3²+4² + 3²+4²+5² - 2×38 = 3
(3-3)² + (4-4)² + (5-5)² = 3²+4²+5² + 3²+4²+5² - 2×50 = 0  <--- here!
(4-3)² + (5-4)² + (6-5)² = 4²+5²+6² + 3²+4²+5² - 2×62 = 5
                           ^^^^^^^^                ^^
                           sliding window          convolution

預先計算每個數字的平方、預先計算各種對齊方式的點積（就是卷積），就可以快速求得a² + b² - 2ab。時間複雜度O(NlogN)。

搜尋（找到零）、最相似（找最小值）、最相異（找最大值）。

http://morris821028.github.io/2015/07/21/zj-b451/

UVa 12298 ICPC 4671 5705 7159

Fourier transform

「傅立葉轉換」。輸入複數數列，輸出複數數列，長度相同。

fourier(x₀ x₁ x₂ x₃ x₄) = (y₀ y₁ y₂ y₃ y₄)

Fourier transform多項式觀點

正向傅立葉轉換（多項式多點求值）：數列變成多項式係數。N次單位根，一共N種。取其倒數，代入多項式，得到N個函數值。

f(x) = x₀x⁰ + x₁x¹ + x₂x² + x₃x³ + x₄x⁴

y₀ = f(ω⁰) = x₀ω⁰ + x₁ω¹ + x₂ω² + x₃ω³ + x₄ω⁴
y₁ = f(ω¹) = x₀ω⁰ + x₁ω² + x₂ω⁴ + x₃ω⁶ + x₄ω⁸
y₂ = f(ω²) = ......
y₃ = f(ω³) = ......
y₄ = f(ω⁴) = ......

where ωᴺ = 1, ω = e-𝑖(2π/N)

逆向傅立葉轉換（多項式內插）：N個函數值，反向推導，得到N個多項式係數。

polynomial function f(x) = c₀x⁰ + c₁x¹ + c₂x² + c₃x³ + c₄x⁴

         Fourier transform
c₀ = x₀  (multipoint evaluation)    f(ω⁰) = y₀
c₁ = x₁ ——————————————————————————→ f(ω¹) = y₁
c₂ = x₂                             f(ω²) = y₂
c₃ = x₃ ←—————————————————————————— f(ω³) = y₃
c₄ = x₄  inverse Fourier transform  f(ω⁴) = y₄
         (interpolation)

註：單位根的數學符號通常是ω。方便起見，本文改成單位根倒數的數學符號是ω，避免數學式子出現一堆負號。

Fourier transform矩陣觀點

「傅立葉矩陣」。傅立葉轉換的變換矩陣。

一、元素：N次單位根（的倒數）的次方。

二、直條：N次單位根（的倒數）的每種次方。

三、每個直條：次方值乘上每種倍率。

    ⎡ ω⁰  ω⁰  ω⁰  ω⁰ .. ⎤ ⎡ x₀ ⎤   ⎡ y₀ ⎤
 1  ⎢ ω⁰  ω¹  ω²  ω³ .. ⎥ ⎢ x₁ ⎥   ⎢ y₁ ⎥
——— ⎢ ω⁰  ω²  ω⁴  ω⁶ .. ⎥ ⎢ x₂ ⎥ = ⎢ y₂ ⎥
√N̅  ⎢ ω⁰  ω³  ω⁶  ω⁹ .. ⎥ ⎢ x₃ ⎥   ⎢ y₃ ⎥
    ⎣ :   :   :   :     ⎦ ⎣ :  ⎦   ⎣ :  ⎦
           Fourier transform

    ⎡ ω⁻⁰ ω⁻⁰ ω⁻⁰ ω⁻⁰ .. ⎤ ⎡ y₀ ⎤   ⎡ x₀ ⎤
 1  ⎢ ω⁻⁰ ω⁻¹ ω⁻² ω⁻³ .. ⎥ ⎢ y₁ ⎥   ⎢ x₁ ⎥
——— ⎢ ω⁻⁰ ω⁻² ω⁻⁴ ω⁻⁶ .. ⎥ ⎢ y₂ ⎥ = ⎢ x₂ ⎥
√N̅  ⎢ ω⁻⁰ ω⁻³ ω⁻⁶ ω⁻⁹ .. ⎥ ⎢ y₃ ⎥   ⎢ x₃ ⎥
    ⎣ :   :   :   :      ⎦ ⎣ :  ⎦   ⎣ :  ⎦
       inverse Fourier transform

正向轉換，使用單位根的倒數e^-𝑖(2π/N)；逆向轉換，使用單位根e^+𝑖(2π/N)。大家顛倒使用，我不知道原因。

正規正交

正交：直條兩兩點積是0。

正規：第一直條長度是√N̅，其餘直條長度是0。全體除以√N̅，令第一直條長度是1，其餘直條長度仍是0。

        ⎡ ω⁰  ω⁰  ω⁰  ω⁰ .. ⎤             ⎡ ω⁻⁰ ω⁻⁰ ω⁻⁰ ω⁻⁰ .. ⎤
     1  ⎢ ω⁰  ω¹  ω²  ω³ .. ⎥          1  ⎢ ω⁻⁰ ω⁻¹ ω⁻² ω⁻³ .. ⎥
F = ——— ⎢ ω⁰  ω²  ω⁴  ω⁶ .. ⎥   F⁻¹ = ——— ⎢ ω⁻⁰ ω⁻² ω⁻⁴ ω⁻⁶ .. ⎥
    √N̅  ⎢ ω⁰  ω³  ω⁶  ω⁹ .. ⎥         √N̅  ⎢ ω⁻⁰ ω⁻³ ω⁻⁶ ω⁻⁹ .. ⎥
        ⎣ :   :   :   :     ⎦             ⎣ :   :   :   :      ⎦

然而，計算√N̅相當費時。大家取消正規。

正向轉換不縮放，逆向轉換除以N。

    ⎡ x⁰  x⁰  x⁰  x⁰ .. ⎤             ⎡ x⁻⁰ x⁻⁰ x⁻⁰ x⁻⁰ .. ⎤
    ⎢ x⁰  x¹  x²  x³ .. ⎥          1  ⎢ x⁻⁰ x⁻¹ x⁻² x⁻³ .. ⎥
F = ⎢ x⁰  x²  x⁴  x⁶ .. ⎥   F⁻¹ = ——— ⎢ x⁻⁰ x⁻² x⁻⁴ x⁻⁶ .. ⎥
    ⎢ x⁰  x³  x⁶  x⁹ .. ⎥          N  ⎢ x⁻⁰ x⁻³ x⁻⁶ x⁻⁹ .. ⎥
    ⎣ :   :   :   :     ⎦             ⎣ :   :   :   :      ⎦

fast fourier transform

直接計算，時間複雜度O(N²)。數列長度是2的次方，則有高速演算法，時間複雜度O(NlogN)。此時稱作「快速傅立葉轉換」。

演算法（Cooley–Tukey algorithm）

原理是dynamic programming。

一、數列長度必須是2的次方，以便對半分。

此例當中，數列長度N = 8 = 2³，總共對半分3回合。

⎡ ω⁰  ω⁰  ω⁰  ω⁰  ω⁰  ω⁰  ω⁰  ω⁰  ⎤ ⎡ x₀ ⎤   ⎡ y₀ ⎤
⎢ ω⁰  ω¹  ω²  ω³  ω⁴  ω⁵  ω⁶  ω⁷  ⎥ ⎢ x₁ ⎥   ⎢ y₁ ⎥
⎢ ω⁰  ω²  ω⁴  ω⁶  ω⁸  ω¹⁰ ω¹² ω¹⁴ ⎥ ⎢ x₂ ⎥   ⎢ y₂ ⎥
⎢ ω⁰  ω³  ω⁶  ω⁹  ω¹² ω¹⁵ ω¹⁸ ω²¹ ⎥ ⎢ x₃ ⎥ = ⎢ y₃ ⎥
⎢ ω⁰  ω⁴  ω⁸  ω¹² ω¹⁶ ω²⁰ ω²⁴ ω²⁸ ⎥ ⎢ x₄ ⎥   ⎢ y₄ ⎥
⎢ ω⁰  ω⁵  ω¹⁰ ω¹⁵ ω²⁰ ω²⁵ ω³⁰ ω³⁵ ⎥ ⎢ x₅ ⎥   ⎢ y₅ ⎥
⎢ ω⁰  ω⁶  ω¹² ω¹⁸ ω²⁴ ω³⁰ ω³⁶ ω⁴² ⎥ ⎢ x₆ ⎥   ⎢ y₆ ⎥
⎣ ω⁰  ω⁷  ω¹⁴ ω²¹ ω²⁸ ω³⁵ ω⁴² ω⁴⁹ ⎦ ⎣ x₇ ⎦   ⎣ y₇ ⎦

二、直條／橫條交換，輸入元素／輸出元素隨之交換。

直條交換，輸入分成偶數項與奇數項，形成分塊。

⎡ ω⁰  ω⁰  ω⁰  ω⁰  │ ω⁰  ω⁰  ω⁰  ω⁰  ⎤ ⎡ x₀ ⎤   ⎡ y₀ ⎤
⎢ ω⁰  ω²  ω⁴  ω⁶  │ ω¹  ω³  ω⁵  ω⁷  ⎥ ⎢ x₂ ⎥   ⎢ y₁ ⎥
⎢ ω⁰  ω⁴  ω⁸  ω¹² │ ω²  ω⁶  ω¹⁰ ω¹⁴ ⎥ ⎢ x₄ ⎥   ⎢ y₂ ⎥
⎢ ω⁰  ω⁶  ω¹² ω¹⁸ │ ω³  ω⁹  ω¹⁵ ω²¹ ⎥ ⎢ x₆ ⎥   ⎢ y₃ ⎥
⎢─────────────────┼─────────────────⎥ ⎢────⎥ = ⎢────⎥
⎢ ω⁰  ω⁸  ω¹⁶ ω²⁴ │ ω⁴  ω¹² ω²⁰ ω²⁸ ⎥ ⎢ x₁ ⎥   ⎢ y₄ ⎥
⎢ ω⁰  ω¹⁰ ω²⁰ ω³⁰ │ ω⁵  ω¹⁵ ω²⁵ ω³⁵ ⎥ ⎢ x₃ ⎥   ⎢ y₅ ⎥
⎢ ω⁰  ω¹² ω²⁴ ω³⁶ │ ω⁶  ω¹⁸ ω³⁰ ω⁴² ⎥ ⎢ x₅ ⎥   ⎢ y₆ ⎥
⎣ ω⁰  ω¹⁴ ω²⁸ ω⁴² │ ω⁷  ω²¹ ω³⁵ ω⁴⁹ ⎦ ⎣ x₇ ⎦   ⎣ y₇ ⎦

三、分塊運算，一道式子變成上下兩道式子。

左分塊是傅立葉轉換（單位根翻倍）。ω⁸ ≡ ω⁰ ≡ 1。

⎡ ω⁰  ω⁰  ω⁰  ω⁰  ⎤ ⎡ x₀ ⎤   ⎡ ω⁰  ω⁰  ω⁰  ω⁰  ⎤ ⎡ x₁ ⎤   ⎡ y₀ ⎤
⎢ ω⁰  ω²  ω⁴  ω⁶  ⎥ ⎢ x₂ ⎥ + ⎢ ω¹  ω³  ω⁵  ω⁷  ⎥ ⎢ x₃ ⎥ = ⎢ y₁ ⎥
⎢ ω⁰  ω⁴  ω⁸  ω¹² ⎥ ⎢ x₄ ⎥   ⎢ ω²  ω⁶  ω¹⁰ ω¹⁴ ⎥ ⎢ x₅ ⎥   ⎢ y₂ ⎥
⎣ ω⁰  ω⁶  ω¹² ω¹⁸ ⎦ ⎣ x₆ ⎦   ⎣ ω³  ω⁹  ω¹⁵ ω²¹ ⎦ ⎣ x₇ ⎦   ⎣ y₃ ⎦

⎡ ω⁰  ω⁸  ω¹⁶ ω²⁴ ⎤ ⎡ x₀ ⎤   ⎡ ω⁴  ω¹² ω²⁰ ω²⁸ ⎤ ⎡ x₁ ⎤   ⎡ y₄ ⎤
⎢ ω⁰  ω¹⁰ ω²⁰ ω³⁰ ⎥ ⎢ x₂ ⎥ + ⎢ ω⁵  ω¹⁵ ω²⁵ ω³⁵ ⎥ ⎢ x₃ ⎥ = ⎢ y₅ ⎥
⎢ ω⁰  ω¹² ω²⁴ ω³⁶ ⎥ ⎢ x₄ ⎥   ⎢ ω⁶  ω¹⁸ ω³⁰ ω⁴² ⎥ ⎢ x₅ ⎥   ⎢ y₆ ⎥
⎣ ω⁰  ω¹⁴ ω²⁸ ω⁴² ⎦ ⎣ x₆ ⎦   ⎣ ω⁷  ω²¹ ω³⁵ ω⁴⁹ ⎦ ⎣ x₇ ⎦   ⎣ y₇ ⎦

四、直條／橫條除以倍率，輸入元素／輸出元素隨之乘以倍率。

右分塊是傅立葉轉換。橫條分別除以ωⁿ，輸出分別乘以ωⁿ。

fft(x₀ x₂ x₄ x₆) + fft(x₁ x₃ x₅ x₇) × (ω⁰ ω¹ ω² ω³) = (y₀ y₁ y₂ y₃)
fft(x₀ x₂ x₄ x₆) + fft(x₁ x₃ x₅ x₇) × (ω⁴ ω⁵ ω⁶ ω⁷) = (y₄ y₅ y₆ y₇)

fft(xeven) + fft(xodd) × ωⁿlow  = ylow 
fft(xeven) + fft(xodd) × ωⁿhigh = yhigh

遞推過程

偶數項與奇數項分開遞歸，形成網路。

重新排列

偶數項與奇數項分開遞歸，索引值不連續。

預先重新排列，減少cache miss，達成inplace。

索引值視作二進位，高低位數顛倒。時間複雜度O(NlogN)。

void reordering(complex<float> x[], int N) { for (int i=1, j=0; i<N; ++i) { for (int k=N>>1; !((j^=k)&k); k>>=1) ; // for (int k=N>>1; k>(j^=k); k>>=1) ; if (i>j) swap(x[i], x[j]); // if (i<j) swap(x[i], x[j]); } }

建立表格。時間複雜度降為O(N)，空間複雜度升為O(N)。

int rev[1<<18]; void reordering(complex<float> x[], int N) { for (int i=0; i<N; i++) rev[i] = (rev[i>>1] | ((i&1) * N)) >> 1; for (int i=0; i<N; i++) if (i < rev[i]) swap(x[i], x[rev[i]]); }

預先建立表格。重複執行傅立葉轉換的情況下，節省時間。

const int lgN = 18; int rev[1<<lgN]; void reordering_init() { for (int i=0; i<1<<lgN; i++) // rev[i] = (rev[i>>1] | ((i&1)<<lgN)) >> 1; rev[i] = (rev[i>>1]>>1) | ((i&1)<<(lgN-1)); } void reordering(complex<float> x[], int N) { int k = lgN - __builtin_ctz(N); for (int i=0; i<N; i++) if (i < rev[i]>>k) swap(x[i], x[rev[i]>>k]); }

ω²ⁿ表格

每回合，ωⁿ的次方值的變化量，變成一半。

一、開方。然而sqrt()時間複雜度不是O(1)。

二、重算。然而sin()和cos()時間複雜度不是O(1)。

三、預先建立表格。以翻倍代替開方。

const int lgN = 18; complex<float> ω2n[lgN]; void ω2n_table(int N, bool type) { float θ = 2.0 * π / N; if (type) θ = -θ; complex<float> ω = polar(1.0f, θ); // complex<float> ω(cos(θ), sin(θ)); int lgN = log2(N); for (int i=0; i<lgN; i++) { ω2n[i] = ω; ω = ω * ω; } }

程式碼

void fft(complex<float> x[], int N, bool type) { reordering(x, N); ω2n_table(N, type); // logN回合 int lgN = log2(N); for (int k=2, n=lgN-1; k<=N; k<<=1, n--) { // 每k個做一次傅立葉轉換 complex<float> ω = ω2n[n]; for (int j=0; j<N; j+=k) { complex<float> ωn(1, 0); for (int i=j; i<j+k/2; i++) { complex<float> a = x[i]; complex<float> b = x[i + k/2] * ωn; x[i] = a + b; x[i + k/2] = a - b; ωn *= ω; } } } if (type) return; for (int i=0; i<N; ++i) x[i] /= N; } void fft(complex<float> x[], int N, bool type) { reordering(x, N); // logN回合 for (int k=2; k<=N; k<<=1) { // 每回合重新計算ωⁿ，程式碼較短，但是速度稍慢。 float θ = 2.0 * π / k; if (type) θ = -θ; complex<float> ω(cos(θ), sin(θ)); // 每k個做一次傅立葉轉換 for (int j=0; j<N; j+=k) { complex<float> ωn(1, 0); for (int i=j; i<j+k/2; i++) { complex<float> a = x[i]; complex<float> b = x[i + k/2] * ωn; x[i] = a + b; x[i + k/2] = a - b; ωn *= ω; } } } if (type) return; for (int i=0; i<N; ++i) x[i] /= N; }

顛倒過程

顛倒過程＝逆向轉換。

一、逆向轉換公式（此例是最後一個步驟，位於網路右下方）。

   ⎰ x̕₆ + x̕₇⋅ω³ = y₃  →  ⎰ x̕₆ + x̕₇⋅ω³ = y₃     where ω⁴ = -1
   ⎱ x̕₆ + x̕₇⋅ω⁷ = y₇     ⎱ x̕₆ - x̕₇⋅ω³ = y₇

→  ⎰ y₃ + y₇ = 2⋅x̕₆     →  ⎰ (y₃ + y₇) / 2 = x̕₆
   ⎱ y₃ - y₇ = 2⋅x̕₇⋅ω³     ⎱ (y₃ - y₇) / ω³ / 2 = x̕₇

二、每回合除以2，改成最後一口氣除以N。節省時間。

三、除以ωⁿ，改成乘以ω⁻ⁿ。節省時間。

演算法（Gentleman–Sande algorithm）

顛倒過程，亦可求得正向轉換：

一、正向轉換、逆向轉換，單位根ω互為倒數。

二、另一個差別：正向轉換不縮放，逆向轉換除以N。

三、逆向轉換＆單位根倒數＆乘以N＝正向轉換。

四、最後一口氣除以N、乘以N，兩者相消。

五、ωⁿ每回合開方，改成每回合翻倍。不必預先建立表格！

程式碼

void fft(complex<float> x[], int N, bool type) { float θ = 2.0 * π / N; if (type) θ = -θ; complex<float> ω = polar(1.0f, θ); // complex<float> ω(cos(θ), sin(θ)); // logN回合 for (int k=N; k>=2; k>>=1, ω*=ω) { // 每k個做一次傅立葉轉換 for (int j=0; j<N; j+=k) { complex<float> ωn(1, 0); for (int i=j; i<j+k/2; i++, ωn*=ω) { complex<float> a = x[i]; complex<float> b = x[i + k/2]; x[i] = a + b; x[i + k/2] = (a - b) * ωn; } } } reordering(x, N); if (type) return; for (int i=0; i<N; ++i) x[i] /= N; } void fft(complex<float> x[], int N, bool type) { float θ = 2.0 * π / N; if (type) θ = -θ; complex<float> ω(cos(θ), sin(θ)); for (int k=N; k>=2; k>>=1) { // 對調內外迴圈，讓ωn少乘幾次。 // 缺點則是索引值更容易跳動，更容易產生cache miss。 complex<float> ωn(1, 0); for (int i=0; i<k/2; i++, ω*=ω) { for (int j=i; j<N; j+=k, ωn*=ω) { complex<float> a = x[j]; complex<float> b = x[j + k/2]; x[j] = a + b; x[j + k/2] = (a - b) * ωn; } } } reordering(x, N); if (type) return; for (int i=0; i<N; ++i) x[i] /= N; } https://maskray.me/blog/2016-10-03-discrete-fourier-transform

number theoretic transform

「數論轉換」。輸入餘數數列，輸出餘數數列，長度相同。

ntt(x₀ x₁ x₂ x₃ x₄) ≡ (y₀ y₁ y₂ y₃ y₄) (mod m)

⎡ ω⁰  ω⁰  ω⁰  ω⁰  ω⁰  ⎤ ⎡ x₀ ⎤   ⎡ y₀ ⎤
⎢ ω⁰  ω¹  ω²  ω³  ω⁴  ⎥ ⎢ x₁ ⎥   ⎢ y₁ ⎥
⎢ ω⁰  ω²  ω⁴  ω⁶  ω⁸  ⎥ ⎢ x₂ ⎥ ≡ ⎢ y₂ ⎥   where ω⁵ ≡ 1 (mod m)
⎢ ω⁰  ω³  ω⁶  ω⁹  ω¹² ⎥ ⎢ x₃ ⎥   ⎢ y₃ ⎥
⎣ ω⁰  ω⁴  ω⁸  ω¹² ω¹⁶ ⎦ ⎣ x₄ ⎦   ⎣ y₄ ⎦

選擇模數

輸入輸出的每個數值都是餘數，大於等於零、小於模數。

當輸入輸出數值很大，那麼模數必須足夠大。

一、數列長度N，單位根ωᴺ ≡ 1，單位根數值皆異。

二、令次方值的模數是N的適當倍數，ord(m) = kN。

三、令模數是質數，根據費馬小定理，m = kN + 1。

四、令模數是質數，存在原根g。

五、令單位根ω ≡ gᵏ，使得ωᴺ ≡ gᵏᴺ ≡ 1。

程式碼

/* a × b ≡ x (mod m) */ long long mul(long long a, long long b, long long m) { long long y = (long long)((double)a*b/m+0.5); long long r = (a*b-y*m) % m; if (r < 0) r += m; return r; } void ntt(long long x[], long long N, bool type) { // 預先算好模數，支援到N = 1<<18。 const long long m = 50000000001507329LL; // 預先算好原根 const long long primitive_root = 3; int ω = pow(primitive_root, m/N, m); if (type) ω = pow(ω, m-2, m); // ω = rec(ω, m) for (int k=N; k>=2; k>>=1) { long long ωn = 1; for (int i=0; i<k/2; i++) { for (int j=i; j<N; j+=k) { long long a = x[j]; long long b = x[j + k/2]; x[j] = add(a, b, m); x[j + k/2] = mul(sub(a, b, m), ωn, m); } ωn = mul(ωn, ω, m); } ω = mul(ω, ω, m); } reordering(x); if (type) return; int rec_n = pow(N, m-2, m); for (int i=0; i<N; ++i) x[i] = mul(x[i], rec_n, m); }

Walsh–Hadamard transform

N=2的傅立葉轉換，推廣到高維度。

矩陣觀點是Hadamard matrix或Walsh matrix。數值都是±1而且向量互相垂直（點積為零）。

http://iris.elf.stuba.sk/JEEEC/data/pdf/09-10_102-10.pdf
http://www.jjj.de/fxt/fxtbook.pdf   p457  p481 $23.8

Hadamard conjecture: size n exists => size 4n exists 
circulant Hadamard matrix conjecture: size n > 4 => never circulant