使用乘法，湊得給定數字。

給你一個數，例如12。哪些數字相乘，可以得到12呢？

例如1×12=12、2×6=12、3×4=12。

使用乘法，分解給定數字。

湊合與分解，一體兩面。12可以分解成哪些數字相乘呢？

例如12=1×12、12=2×6、12=3×4。

一個數字分解成的數字叫做「因數」。

Divisor Generation

「因數生成」。一個數字的所有因數，通通列出來。

0: 0 1 2 ...   5: 1 5       10: 1 2 5 10
1: 1           6: 1 2 3 6   11: 1 11
2: 1 2         7: 1 7       12: 1 2 3 4 6 12
3: 1 3         8: 1 2 4 8   13: 1 13
4: 1 2 4       9: 1 3 9     14: 1 2 7 14

一個數字的所有因數

「試除法」。嘗試每個數字作為因數。時間複雜度O(n)。

void divisor_generation(int n) { for (int d=1; d<=n; d++) if (n % d == 0) cout << d << "是因數"; } vector<int> divisor; void divisor_generation(int n) { for (int i=1; i<=n; i++) // 窮舉因數 if (n % i == 0) divisor.push_back(i); }

因數成雙成對

因數成雙成對（平方根跟自己一對），窮舉一半足矣。

乘法分解的一半：平方根。時間複雜度降為O(sqrt(n))。

void divisor_generation(int n) { int d; // for (d=1; d<sqrt(n); d++) for (d=1; d*d<n; d++) if (n % d == 0) { cout << d << "是因數"; cout << n / d << "是因數"; } if (d*d == n) cout << d << "是因數"; }

時間複雜度

注意到此處的時間複雜度O(n) = O(2ᴺ)，屬於指數時間！

n是數值大小，不是數據數量。n視作二進位數字，n = 2ᴺ，N是位數大小，才是數據數量。

多項式時間　O(log(n))  = O(N)
多項式時間　O(log²(n)) = O(N²)
指數時間　　O(n)       = O(2ᴺ)
指數時間　　O(n⋅log(n)) = O(2ᴺ⋅N)
指數時間　　O(n²)      = O(2²ᴺ)

注意到此處的時間複雜度O(n)，整數運算預設為O(1)！

認真考慮整數運算，得到時間複雜度O(n log²(n))。

整數　　　　　　　　　a = 2ᴬ , b = 2ᴮ , n = 2ᴺ
整數加法、整數減法　　O(A+B) = O(log(a)+log(b)) = O(log(n))
整數乘法、整數除法　　O(A⋅B) = O(log(a)⋅log(b)) = O(log²(n))　還可以更低
整數移位　　　　　　　O(N) = O(log(n))
整數變號、整數絕對值　O(N) = O(log(n))
整數比大小、整數交換　O(A+B) = O(log(a)+log(b)) = O(log(n))

每個數字的所有因數

「篩法」。窮舉因數、篩選倍數。時間複雜度O(NlogN)。

const int N = 20000000; vector<int> divisor[N]; void divisor_generation() { for (int i=1; i<=N; i++) // 窮舉因數 for (int j=i; j<=N; j+=i) // 篩選倍數 divisor[j].push_back(i); }

時間複雜度

注意到此處的時間複雜度O(NlogN)，源自迴圈執行次數！

調和級數儘管發散，但是擁有界限。

1/1 + 1/2 + 1/3 + ... + 1/N = O(logN)
N/1 + N/2 + N/3 + ... + N/N = O(NlogN)

注意到此處的時間複雜度O(NlogN)，屬於多項式時間！

數值大小視作數據數量。位數大小不再視作數據數量，而是視作常數，讓整數運算預設為O(1)。

多項式時間　O(N)
多項式時間　O(NlogN)
多項式時間　O(N²)
指數時間　　O(2ᴺ)
指數時間　　O(Nᴺ)

Greatest Common Divisor

「最大公因數」。大家都有的因數們，當中最大的一個。

0: 0 1 2 ...   5: 1 5       10: 1 2 5 10
1: 1           6: 1 2 3 6   11: 1 11
2: 1 2         7: 1 7       12: 1 2 3 4 6 12
3: 1 3         8: 1 2 4 8   13: 1 13
4: 1 2 4       9: 1 3 9     14: 1 2 7 14

gcd(8, 8, 8, 8, 8) = 8
gcd(6, 9, 12) = 3
gcd(2, 3, 5, 7, 11) = 1
gcd(1, 8) = 1
gcd(0, 8) = 8

可以直接使用C++標準函式庫的gcd()。

Least Common Multiple

「最小公倍數」。大家都有的倍數們，當中最小的一個。

數學公式：gcd(a,b) ⋅ lcm(a,b) = ab。

最大公因數的遞歸性質

任取幾個數字，換成它們的最大公因數，最終答案不變。

不斷精簡，直到剩下兩數。兩數的最大公因數，請見後面章節。

把最大公因數想成是疊積木就簡單多了。

int gcd(int a, int b, int c) { return gcd(gcd(a, b), c); } template<typename... Args> int gcd(int a, int b, Args... args) { return gcd(a, gcd(b, args...)); }

Trial Division Algorithm

「試除法」。嘗試每個數字作為最大公因數。時間複雜度O(min(a,b))。

int gcd(int a, int b) { int d = min(a, b); if (d == 0) return 0; while (!(a%d==0 && b%d==0)) d--; return d; }

因數成雙成對（平方根跟自己一對），窮舉一半足矣。乘法分解的一半：平方根。時間複雜度降為O(sqrt(min(a,b)))。

int gcd(int a, int b) { if (a > b) swap(a, b); if (a == 0) return 0; int maxd = 1; for (int d=2; d*d<=a; ++d) if (a % d == 0) { // d是a的因數 if (b % d == 0) maxd = max(maxd, d); // a/d是a的因數 if (b % (a/d) == 0) maxd = max(maxd, a/d); } return maxd; }

Euclidean Algorithm（Euclid's Algorithm）

幾何學之父歐幾里德所發明的「輾轉相除法」，用來求兩數的最大公因數。幾何學之父原來跟數論也扯得上關係。

由於兩數必定是由最大公因數的整數倍所組合而成，故其差值也必定由最大公因數的整數倍所組合而成，不管兩數如何輾轉相減、輾轉求餘數，其得到的值都會是最大公因數的倍數。把最大公因數想成是疊積木就簡單多了。

求出了差值後，原問題便縮小成了跟原問題類似的問題。也就是說，輾轉相除法採取了Divide-and-Conquer Method。

時間複雜度O(log(min(a,b)))，其中整數運算預設為O(1)。原理是Fibonacci Sequence，詳情請見離散數學教科書。

迴圈版本。

// 令 a 大 b 小，比較容易思考。 int gcd(int a, int b) { // 大小不對，交換位置。 if (a < b) return gcd(b, a); while (b != 0) { int r = a % b; a = b; b = r; } // 如果比較小的數字為零，表示比較大的數字為最大公因數。 return a; } // 其實不必偵測 a b 大小，自己便會交換。 int gcd(int a, int b) { while (b != 0) { int r = a % b; a = b; b = r; } return a; } // 奇怪的迴圈版本。僅供參考。 int gcd(int a, int b) { if (a == 0 || b == 0) return a + b; while ((a %= b) && (b %= a)) /* empty */; return a + b; }

遞迴版本。

// 令 a 大 b 小，比較容易思考。 int gcd(int a, int b) { // 大小不對，交換位置。 if (a < b) return gcd(b, a); // 如果比較小的數字為零，表示比較大的數字為最大公因數。 if (b == 0) return a; // 輾轉相除 return gcd(b, a%b); } int gcd(int a, int b) { if (a < b) return gcd(b, a); return b==0 ? a : gcd(b, a%b); // 連成一氣 } // 其實不必偵測 a b 大小，自己便會交換。 int gcd(int a, int b) { return b==0 ? a : gcd(b, a%b); } int gcd(int a, int b) { return b ? gcd(b, a%b) : a; }

UVa 10193 10407

Binary GCD Algorithm

二進位數字的最大公因數計算方法。漢朝數學著作《九章算術》稱之為「更相減損術」。

如果 a b 有一個是零    	⇒ gcd(a, b) = a和b當中不是零的那個數
如果 a b 都是偶數      	⇒ gcd(a, b) = gcd(a/2, b/2) × 2
如果 a 是偶數  b 是奇數	⇒ gcd(a, b) = gcd(a/2, b)
如果 a 是奇數  b 是偶數	⇒ gcd(a, b) = gcd(a, b/2)
如果 a b 都是奇數      	⇒ gcd(a, b) = gcd(a和b比較小那個數, a和b的差)

電腦裡的數字都是用二進位儲存的──要乘以二，就把數字的每個bit都左移一個bit；要除以二，就把數字的每個bit都右移一個bit（別忘記補零）。位移運算比除法運算還要快，於是便開發了以提取因數二來計算最大公因數的方法。

歸納要點：甲、不斷提取共同的因數，都只提取二；乙、二與奇數互質，不會影響最大公因數，故可除去二；丙、若無因數二則相減，相減後仍是最大公因數的倍數。

時間複雜度仍是O(log(min(a,b)))，其中整數運算預設為O(1)。認真考慮整數運算，由於沒有整數除法，時間複雜度其實較低。

int gcd(int a, int b) { if (a == 0) return b; if (b == 0) return a; if ((a & 1) == 0 && (b & 1) == 0) return gcd(a >> 1, b >> 1) << 1; else if ((a & 1) == 0) return gcd(a >> 1, b); else if ((b & 1) == 0) return gcd(a, b >> 1); else return gcd(min(a, b), abs(a - b)); } int gcd(int a, int b) { int c = 0; // 記錄 gcd 乘二乘了幾次 while (a && b) // 如果 a b 都是正數 // 如果 a b 都是偶數：a /= 2, b /= 2, gcd 乘二 if (!(a & 1) && !(b & 1)) a >>= 1, b >>= 1, c++; // 如果 a 是偶數、b 是奇數：a /= 2 else if (!(a & 1)) a >>= 1; // 如果 a 是奇數、b 是偶數：b /= 2 else if (!(b & 1)) b >>= 1; // 如果 a b 都是奇數：判斷 a b 大小，求出餘數。 else if (a > b) a -= b; else b -= a; // 不為零的數，乘上 c 個 2，就是 gcd。 return max(a, b) << c; } int gcd(int a, int b) { int c = 0; while (!(a & 1) && !(b & 1)) a >>= 1, b >>= 1, c++; while (a) if (!(a & 1)) a >>= 1; else if (!(b & 1)) b >>= 1; else { int r = abs(a-b) >> 1; if (a < b) b = r; else a = r; } return b << c; }

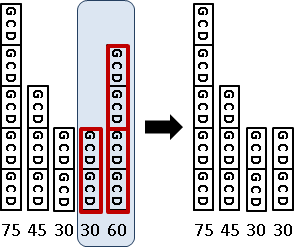
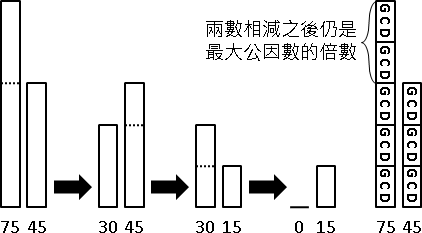
Extended Euclidean Algorithm

輾轉相除法的擴展版本。除了可以找出兩數的最大公因數，還可以順便找出此兩數各乘上多少整數倍率後相加可得到最大公因數（倍率可以是負數或零），並且讓兩個整數倍率的絕對值都最小。

以數學符號來表示，擴展輾轉相除法可以找出a b兩數的最大公因數d，還可以順便找出滿足ai + bj = d的兩個整數倍率i j，並且讓|i|與|j|最小。

遞推法。複製a b成為u v，以u v兩數進行輾轉相除。建立整數倍率iᵤ jᵤ iᵥ jᵥ，使得aiᵤ + bjᵤ = u且aiᵥ + bjᵥ = v。根據輾轉相除數學式子u - qv = r，推得(aiᵤ + bjᵤ) - q (aiᵥ + bjᵥ) = a (iᵤ - qiᵥ) + b (jᵤ - qjᵥ) = r。如此一來就知道新的整數倍率iᵣ jᵣ了。

void extgcd(int a, int b, int& i, int& j, int& d) { int i_ = 1, j_ = 0; // a i = 0, j = 1; // b while (true) { int q = a / b, r = a % b, t; if (r == 0) break; a = b; b = r; t = i_; i_ = i; i = t - q * i; t = j_; j_ = j; j = t - q * j; } d = b; }

遞歸法。以Divide-and-Conquer Method的Combine階段來計算i j。當問題分割至最小，此時可以明確的、輕鬆的算出i j的值。每次合併問題，就重新調整i j，保持|i|與|j|最小。

// 令 a 大 b 小，比較容易思考。 void extgcd(int a, int b, int& i, int& j, int& d) { // 問題已分割至最小，i j 很好算。 if (b == 0) { d = a; // 最大公因數為 a i = 1; j = 0; // 此時的 i j return; } // Divide + Conquer：輾轉相除。 extgcd(b, a % b, i, j, d); // Combine：利用小問題的結果，計算出現在這個問題的 i j。 int t = i; i = j; j = t - (a / b) * j; } void extgcd(int a, int b, int& i, int& j, int& d) { if (b == 0) {d = a; i = 1; j = 0; return;} extgcd(b, a % b, j, i, d); j -= (a / b) * i; }

UVa 10104

Bézout's Identity（Linear Diophantine Equation）

已知a b c，求出x y，使得ax + by = c。

一、擴展輾轉相除法：
　　求得 ai + bj = d，其中 d = gcd(a, b)。
二、得到其中一組解：
　甲、檢查d的倍數是不是c。
　　回、如果是：
　　　　整個式子乘上c/d，讓d變成c，
　　　　式子變成 aic/d + bjc/d = c -①
　　　　顯然 (x,y) = (ic/d, jc/d) 就是其中一組解！
　　回、如果不是：
　　　　無解！
三、得到所有解：
　甲、首先製造一個式子 a(?) + b(?) = 0 目的是要等於零。
　　　直覺就能想到 ab + b(-a) = 0
　　　更進一步想到 ab/d + b(-a)/d = 0 -②
　乙、式子①加上式子②的各種倍率，也就是①+②×k：
　　　a(ic/d + kb/d) + b(jc/d - ka/d) = 0，其中k是整數。
　　　顯然 (x,y) = (ic/d + kb/d, jc/d - ka/d) 就是所有解！
四、得到所有非負整數解（假設a b為正數）：
　甲、也就是說，(ic/d + kb/d)與(jc/d - ka/d) 必須是非負整數。
　　　(ic/d + kb/d) ≥ 0  ⇒  k ≥ -ic/b
　　　(jc/d - ka/d) ≥ 0  ⇒  k ≤ +jc/a
　　　 -ic/b  ≤ k ≤  +jc/a
　　　⌈-ic/b⌉ ≤ k ≤ ⌊+jc/a⌋
　　　因為k是整數，所以取天花板和地板。進而得到所有非負整數解。

UVa 10090 10548 10413 11312 luogu P4549 P2833