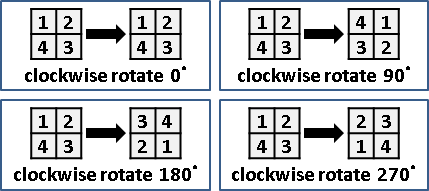
group
「群」是兩種東西合體:多個元素(一個集合)、一個運算。必須滿足四個規定。
1. closure 閉包:無論取誰運算,結果仍是那些元素。
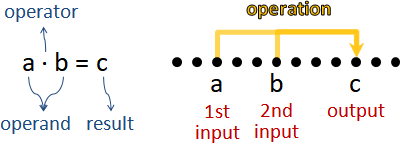
a∙b = c
a∈S, b∈S ⇒ c∈S
2. associativitiy 結合律:無論誰先運算,結果一致。
(a∙b)∙c = a∙(b∙c)
3. identity 單位元素1:實施運算,結果不變。
a∙1 = 1∙a = a
4. inverse 反元素a̅:實施運算,結果相消,得到單位元素。
a∙a̅ = a̅∙a = 1
所有元素必須符合所有規定。
a b c:任意元素。
1 a̅:符合規定的某個元素(某些元素)。必須找到。
順便介紹一下其他數學符號的意義。
S:這個群的元素們(集合)。
∙:這個群的運算。
=:等於。詳情請自行學習集合論。
∈:屬於。詳情請自行學習集合論。
,:與。詳情請自行學習集合論。
範例:整數加法群
集合:整數ℤ ℤ = {..., -2, -1, 0, 1, 2, ...}
運算:整數加法+
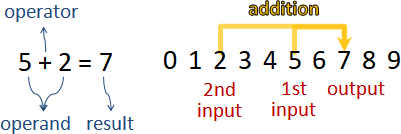
1. 2+3 = 5 a = 2, b = 3, c = 5
2∈ℤ, 3∈ℤ ⇒ 5∈ℤ
2. (2+3)+4 = 2+(3+4) a = 2, b = 3, c = 4
3. 2+0 = 0+2 = 2 a = 2, 1 = 0
4. 2+(-2) = (-2)+2 = 0 a = 2, a̅ = -2, 1 = 0
範例:整數乘法群
集合:整數ℤ ℤ = {..., -2, -1, 0, 1, 2, ...}
運算:整數加法×
1. 2×3 = 6 a = 2, b = 3, c = 6
2∈ℤ, 3∈ℤ ⇒ 6∈ℤ
2. (2×3)×4 = 2×(3×4) a = 2, b = 3, c = 4
3. 2×1 = 1×2 = 2 a = 2, 1 = 1
4. 2×½ = ½×2 = 1 a = 2, a̅ = ½, 1 = 1
範例:餘數加法群
集合:餘數ℤₙ ℤ₅ = {0, 1, 2, 3, 4}
運算:餘數加法+
1. 2+3 ≡ 0 (mod 5) a = 2, b = 3, c = 0
2∈ℤ₅, 3∈ℤ₅ ⇒ 0∈ℤ₅
2. (2+3)+4 ≡ 2+(3+4) (mod 5) a = 2, b = 3, c = 4
3. 2+0 ≡ 0+2 ≡ 2 (mod 5) a = 2, 1 = 0
4. 2+3 ≡ 3+2 ≡ 0 (mod 5) a = 2, a̅ = 3, 1 = 0
範例:餘數乘法群
集合:與模數互質的數字ℤₙˣ ℤ₈ˣ = {1, 3, 5, 7}
運算:餘數乘法×
1. 3×5 ≡ 7 (mod 8) a = 3, b = 5, c = 7
3∈ℤ₈ˣ, 5∈ℤ₈ˣ ⇒ 7∈ℤ₈ˣ
2. (3×5)×7 ≡ 3×(5×7) (mod 8) a = 3, b = 5, c = 7
3. 5×1 ≡ 1×5 ≡ 5 (mod 8) a = 5, 1 = 1
4. 5×5 ≡ 5×5 ≡ 1 (mod 8) a = 5, a̅ = 5, 1 = 1
反例:向量叉積
集合:實數向量ℝₙ
運算:向量叉積×
2. (a×b)×c ≠ a×(b×c)
結合律不存在。
想要體現非群,我認為向量叉積是經典反例。
commutative group(Abelian group)
「交換群」。追加第五點規則。
5. commutativity 交換律:輸入交換順序,輸出仍然相同。
a∙b = b∙a
追加規則聽起來很煩。其實可以把事情想得簡單一點:群分成兩種,要嘛符合交換律,要嘛不符合交換律。
方才的範例都是交換群。下面補充兩個不是交換群的範例。
反例:矩陣乘法群
集合:可逆矩陣
運算:矩陣乘法
1. ⎡ 1 2 ⎤ ⎡ 2 2 ⎤ = ⎡ 8 10 ⎤
⎣ 3 4 ⎦ ⎣ 3 4 ⎦ ⎣ 18 22 ⎦
⎡ 1 2 ⎤ ∈ ℝ₂ₓ₂ ⎡ 2 2 ⎤ ∈ ℝ₂ₓ₂ ⇒ ⎡ 8 10 ⎤ ∈ ℝ₂ₓ₂
⎣ 3 4 ⎦ , ⎣ 3 4 ⎦ ⎣ 18 22 ⎦
a = ⎡ 1 2 ⎤ b = ⎡ 2 2 ⎤ c = ⎡ 8 10 ⎤
⎣ 3 4 ⎦ , ⎣ 3 4 ⎦ , ⎣ 18 22 ⎦
2. ⎛ ⎡ 1 2 ⎤ ⎡ 2 2 ⎤ ⎞ ⎡ 3 2 ⎤ = ⎡ 1 2 ⎤ ⎛ ⎡ 2 2 ⎤ ⎡ 3 2 ⎤ ⎞
⎝ ⎣ 3 4 ⎦ ⎣ 3 4 ⎦ ⎠ ⎣ 3 4 ⎦ ⎣ 3 4 ⎦ ⎝ ⎣ 3 4 ⎦ ⎣ 3 4 ⎦ ⎠
a = ⎡ 1 2 ⎤ , b = ⎡ 2 2 ⎤ , c = ⎡ 3 2 ⎤
⎣ 3 4 ⎦ ⎣ 3 4 ⎦ ⎣ 3 4 ⎦
3. ⎡ 4 3 ⎤ ⎡ 1 0 ⎤ = ⎡ 1 0 ⎤ ⎡ 4 3 ⎤ = ⎡ 4 3 ⎤
⎣ 3 2 ⎦ ⎣ 0 1 ⎦ ⎣ 0 1 ⎦ ⎣ 3 2 ⎦ ⎣ 3 2 ⎦
a = ⎡ 4 3 ⎤ , 1 = ⎡ 1 0 ⎤
⎣ 3 2 ⎦ ⎣ 0 1 ⎦
4. ⎡ 4 3 ⎤ ⎡ -2 3 ⎤ = ⎡ -2 3 ⎤ ⎡ 4 3 ⎤ = ⎡ 1 0 ⎤
⎣ 3 2 ⎦ ⎣ 3 4 ⎦ ⎣ 3 4 ⎦ ⎣ 3 2 ⎦ ⎣ 0 1 ⎦
a = ⎡ 4 3 ⎤ , a̅ = ⎡ -2 3 ⎤ , 1 = ⎡ 1 0 ⎤
⎣ 3 2 ⎦ ⎣ 3 4 ⎦ ⎣ 0 1 ⎦
5. ⎡ 1 2 ⎤ ⎡ 2 2 ⎤ ≠ ⎡ 2 2 ⎤ ⎡ 1 2 ⎤
⎣ 3 4 ⎦ ⎣ 3 4 ⎦ ⎣ 3 4 ⎦ ⎣ 3 4 ⎦
a = ⎡ 1 2 ⎤ , b = ⎡ 2 2 ⎤
⎣ 3 4 ⎦ ⎣ 3 4 ⎦
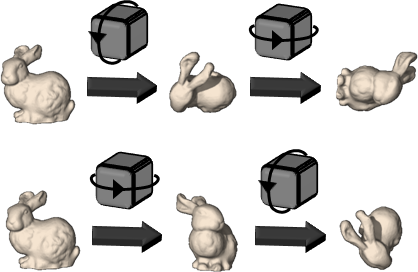
反例:三維旋轉群SO(3)
集合:三維旋轉矩陣(正規正交矩陣,determinant是1)
運算:矩陣乘法
先轉後轉,結果不同。
想要體現非交換群,我認為三維旋轉群是經典反例。
order
「秩」。群的大小。元素數量。集合大小。
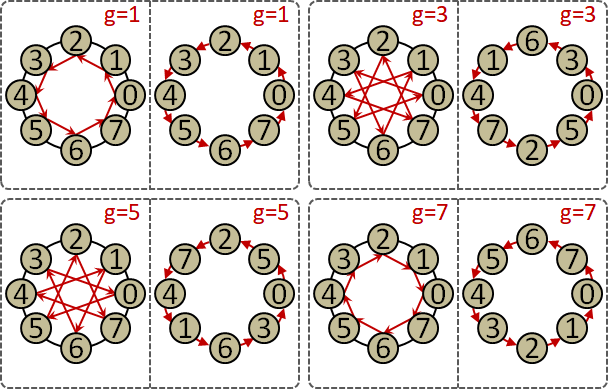
generating set
「生成集合」。取出一些元素。以這些元素及其反元素,實施一長串運算,例如a∙b∙a̅∙b∙b∙b,可以得到每一種元素。
白話:萬能材料。
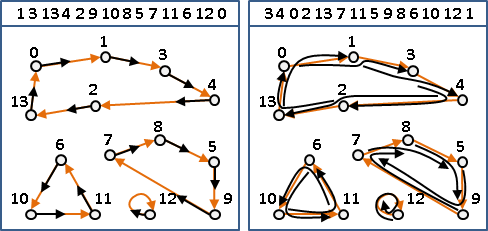
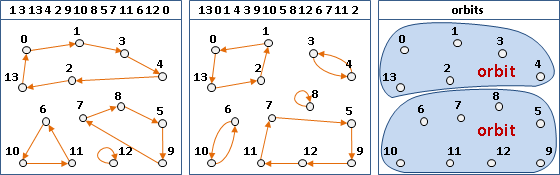
subgroup
「子群」。取出一些元素。以這些元素及其反元素,實施一長串運算,還是只能得到這些元素。
白話:關住了、出不去了。
註:教科書採用遞推版本「運算結果及其反元素,反覆實施運算」。兩種版本等價。反元素唯一、反反元素是自身a̿ = a、反元素公式a ∙ b = b ∙ a,證明這三者,接著就能證明兩種版本等價。
數學定理
Lagrange's theorem:子群的大小,整除群的大小。
Cauchy's theorem:當質數p整除群的大小(例如排列群),那麼此群存在一個元素g(例如一個排列),使得 g^p = 1(此排列套用p次,每個軌道剛好走零步)。
Cayley's theorem:隨便一個群,一定可以等價地變成某個對稱群的子群(例如排列群)。
延伸閱讀