filter
filter
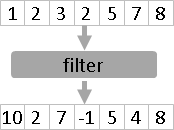
「濾波器」。輸入一串數列、輸出一串數列的函數。
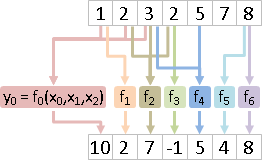
每個輸出變數分開來看,濾波器其實是由許多函數組成。
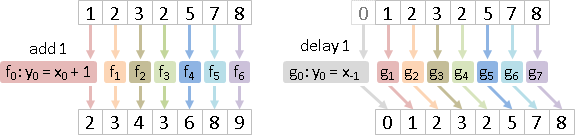
簡單的例子是每項加1的濾波器、每項延遲1時刻的濾波器。
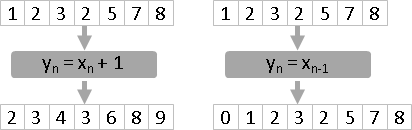
當全部函數都相同,僅索引值(時刻)不同,可以簡化成一個函數。
filter
filter
「濾波器」。輸入一串數列、輸出一串數列的函數。

每個輸出變數分開來看,濾波器其實是由許多函數組成。

簡單的例子是每項加1的濾波器、每項延遲1時刻的濾波器。

當全部函數都相同,僅索引值(時刻)不同,可以簡化成一個函數。

linear time-invariant filter
linear time-invariant filter(LTI filter)
「線性非時變濾波器」。濾波器是相同的線性函數。
數學家和計算學家擅長線性函數,容易計算。
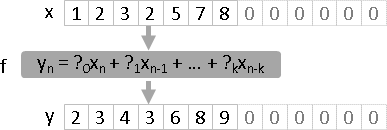
數列x,通過濾波器a,得到數列y。
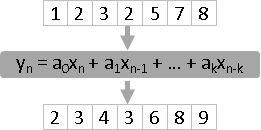
linear time-invariant filter可以寫成線性組合形式
濾波器視作權重。
y(n) = a(0)x(n) + a(1)x(n-1) + a(2)x(n-2) + ... + a(k)x(n-k)
linear time-invariant filter可以寫成矩陣形式
濾波器視作矩陣。
⎡ a(0) 0 0 ... 0 0 0 ⎤ ⎡ x(0) ⎤ ⎡ y(0) ⎤
⎢ a(1) a(0) 0 ... 0 0 0 ⎥ ⎢ x(1) ⎥ ⎢ y(1) ⎥
⎢ a(2) a(1) a(0) ... 0 0 0 ⎥ ⎢ : ⎥ ⎢ : ⎥
⎢ : : : : : : ⎥ ⎢ : ⎥ = ⎢ : ⎥
⎢ 0 0 0 ... a(0) 0 0 ⎥ ⎢ : ⎥ ⎢ : ⎥
⎢ 0 0 0 ... a(1) a(0) 0 ⎥ ⎢ : ⎥ ⎢ : ⎥
⎣ 0 0 0 ... a(2) a(1) a(0) ⎦ ⎣ x(n) ⎦ ⎣ y(n) ⎦
A x y
數列x視作矩陣。
⎡ x(0) 0 ... 0 0 ⎤ ⎡ y(0) ⎤
⎢ x(1) x(0) ... 0 0 ⎥ ⎡ a(0) ⎤ ⎢ y(1) ⎥
⎢ : : : : ⎥ ⎢ a(1) ⎥ ⎢ : ⎥
⎢ : : : : ⎥ ⎢ : ⎥ = ⎢ : ⎥
⎢ : : : : ⎥ ⎢ : ⎥ ⎢ : ⎥
⎢ x(n-1) x(n-2) ... x(n-k) x(n-k-1) ⎥ ⎣ a(k) ⎦ ⎢ : ⎥
⎣ x(n) x(n-1) ... x(n-k+1) x(n-k) ⎦ ⎣ y(n) ⎦
X a y
linear time-invariant filter可以寫成卷積形式
數列末端補零K個。
( x(0) .. x(n) 0 .. 0 ) ∙ ( a(0) ) = y(0)
( x(0) .. x(n) 0 .. 0 ) ∙ ( a(1) a(0) ) = y(1)
: : :
( x(0) .. x(n) 0 .. 0 ) ∙ ( a(k) ....... a(0) ) = y(n-1)
( x(0) .. x(n) 0 .. 0 ) ∙ ( a(k) ....... a(0) ) = y(n)
—————————————————————————————————————————————————————————————————
( x(0) .. x(n) 0 .. 0 ) ∙ ( a(k) .. a(1) ) = 0
: : :
( x(0) .. x(n) 0 .. 0 ) ∙ ( a(k) ) = 0
x' ∗ a = y'
linear time-invariant filter運算
evaluation (moving average): f(x) = ? , find y resolution (deconvolution): f(?) = y , find x regression (Wiener filter): ?(x) = y , find f inversion: f(x) = y , x = ?(y) , find f⁻¹
四種運算:求值(通過濾波器)、求解(反向通過濾波器)、迴歸(求濾波器)、反函數(求反濾波器)。
四種運算都有時域和頻域兩種解法。頻域解法的時間複雜度較低,但是沒人用!一、濾波器長度通常很短(函數項數很少),傅立葉轉換反而浪費時間。二、濾波器無法完美轉換到頻域。
求值(通過濾波器)
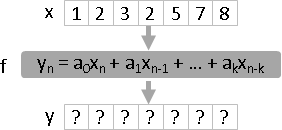
evaluation (moving average): f(x) = ? , find y
滑動視窗,取加權平均數。時間複雜度O(NK)。
求解(反向通過濾波器)
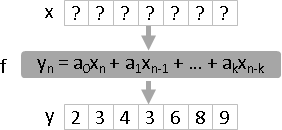
resolution (deconvolution): f(?) = y , find x
滑動視窗,解加權平均數方程式。時間複雜度O(NK)。
迴歸(求濾波器)
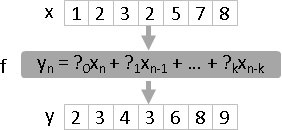
regression (Wiener filter): ?(x) = y , find f
數列x視作矩陣。等式太多,通常無解。改為找到平方誤差最小的解,套用「normal equation」。時間複雜度O(N³)。
⎡ x(0) 0 ... 0 0 ⎤ ⎡ y(0) ⎤
⎢ x(1) x(0) ... 0 0 ⎥ ⎡ a(0) ⎤ ⎢ y(1) ⎥
⎢ : : : : ⎥ ⎢ a(1) ⎥ ⎢ : ⎥
⎢ : : : : ⎥ ⎢ : ⎥ = ⎢ : ⎥
⎢ : : : : ⎥ ⎢ : ⎥ ⎢ : ⎥
⎢ x(n-1) x(n-2) ... x(n-k) x(n-k-1) ⎥ ⎣ a(k) ⎦ ⎢ : ⎥
⎣ x(n) x(n-1) ... x(n-k+1) x(n-k) ⎦ ⎣ y(n) ⎦
X a y
對應項平方誤差總和最小,即是滿足 Xᵀ X a = Xᵀ y。
a = (Xᵀ X)⁻¹ Xᵀ y
旁門左道的解法是Wiener–Hopf equation。
數列末端補零K個,讓矩陣變漂亮。答案不對,但是算得快。
一、建立矩陣:卷積。O(NK)甚至O(NlogN)。
二、矩陣求解:循環矩陣求解。O(K²)甚至O(KlogK)。
⎡ x(0) ⎤ ⎡ y(0) ⎤
⎢ : x(0) ⎥ ⎢ : ⎥
⎢ : : ⎥ ⎡ a(0) ⎤ ⎢ : ⎥
⎢ : : x(0) ⎥ ⎢ : ⎥ ⎢ : ⎥
⎢ : : ..... : x(0) ⎥ ⎢ : ⎥ = ⎢ : ⎥
⎢ x(n) : : : ⎥ ⎢ : ⎥ ⎢ y(n) ⎥
⎢ x(n) : : ⎥ ⎣ a(k) ⎦ ⎢ 0 ⎥
⎢ : : ⎥ ⎢ : ⎥
⎢ x(n) : ⎥ ⎢ : ⎥
⎣ x(n) ⎦ ⎣ 0 ⎦
X a y
⎡ xx(0) xx(1) ... xx(k) ⎤ ⎡ a(0) ⎤ ⎡ xy(0) ⎤
⎢ xx(1) xx(0) ... xx(k-1) ⎥ ⎢ a(1) ⎥ ⎢ xy(1) ⎥
⎢ : : : ⎥ ⎢ : ⎥ = ⎢ : ⎥
⎢ xx(k-1) xx(k-2) ... xx(1) ⎥ ⎢ : ⎥ ⎢ : ⎥
⎣ xx(k) xx(k-1) ... xx(0) ⎦ ⎣ a(k) ⎦ ⎣ xy(k) ⎦
Xᵀ X a Xᵀ y
xx(t) = ∑ x(i-t)⋅x(i) autocorrelation of x(i-t) and x(i).
xy(t) = ∑ x(i-t)⋅y(i) cross-correlation of x(i-t) and y(i).
對應項平方誤差總和最小,即是滿足 Xᵀ X a = Xᵀ y。
Xᵀ X 和 Xᵀ y 乘起來,稱作Wiener–Hopf equation。
xx(t):數列x延遲t時刻、數列x,兩者的自相關數(相差t時刻,兩串相同數列的點積)。
xy(t):數列x延遲t時刻、數列y,兩者的互相關數(相差t時刻,兩串不同數列的點積)。
反函數(求反濾波器)
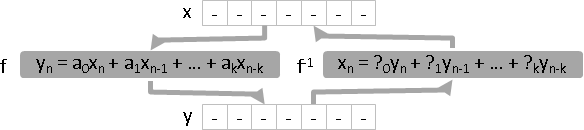
inversion: f(x) = y , x = ?(y) , find f⁻¹
濾波器通常不是一對一函數,通常不存在反函數。什麼時候存在反函數呢?我查不到相關資料!
我也沒找到反函數演算法!目前有兩種做法:
一、隨便找一組輸出輸入,對調一下,然後迴歸。
二、濾波器,轉換到頻域,取倒數,轉換回時域。
延伸閱讀:linear time-invariant的定義
linear time-invariant(連續函數)與linear shift-invariant(離散數列)是指同時滿足三種特性:加性、倍性、移位性。
function of a sequence
F(x(n)) = y(n)
1. additive function
F(x₁(n) + x₂(n)) = y₁(n) + y₂(n)
2. homogeneous function of order 1
F(k x(n)) = k y(n)
3. shiftable function / shift-invariant function
F(x(n + m)) = y(n + m)
def
linear === 1 and 2
def
linear shift-invariant === 1 and 2 and 3
移位性:輸入數列移位,等同於輸出數列移位。
曾訊號學者提出shiftable這個詞彙。然而大家不採用。
訊號學者採用time-invariant(連續函數)與shift-invariant(離散數列)這兩個詞彙。然而X-invariant有兩種定義。這兩個詞彙屬於第二種定義。
1. F(X(x(n))) = F(x(n)) = y(n) 2. F(X(x(n))) = X(y(n))
linear recurrence
linear recurrence
遞迴數列可以視作數列暨濾波器:輸入與輸出是同一數列,但是輸出延遲1時刻。
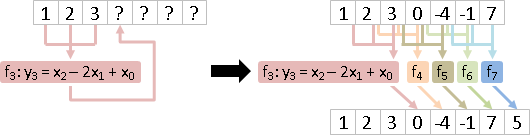
linear recurrence運算
evaluation: f(?) = ? >> 1 , find x autoregression: ?(x) = x >> 1 , find f
兩種運算:求值(求遞迴數列)、自迴歸(求遞迴函數)。
求值(求遞迴數列)
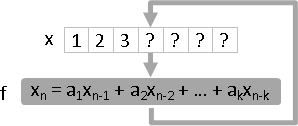
evaluation: f(?) = ? >> 1 , find x
線性遞迴函數K項,求數列第N項,總共三種方法:
一、動態規劃,第0項算到第N項。O(NK)。
二、同伴矩陣的N次方。O(K³logN)。假設矩陣相乘O(K³)。
三、xᴺ模特徵多項式。O(K²logN)甚至O(KlogKlogN)。
當K是常數,一變成O(N),二三變成O(logN)。
自迴歸(求遞迴函數)
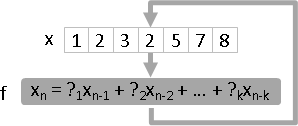
autoregression: ?(x) = x >> 1 , find f
每一個數值,皆是先前緊鄰的K個數值的加權總和,權重是定值。反覆套用線性遞迴函數、代入數列最後N個數值,就能預測下一個即將出現的數值。此行為稱作「線性預測linear prediction」。
一串長長的數列,壓縮成一個線性遞迴函數,只需儲存K個函數係數、K個初始數值。反覆套用函數、代入數列最後K個數值,解壓縮得到一串長長的數列。此行為稱作「線性預測編碼linear predictive coding」。
演算法是Berlekamp–Massey algorithm。時間複雜度O(NK)。
旁門左道的解法是Yule–Walker equation。
數列末端補零K個,讓矩陣變漂亮。答案不對,但是算得快。
一、建立矩陣:卷積。O(NK)甚至O(NlogN)。
二、矩陣求解:循環矩陣求解。O(K²)甚至O(KlogK)。
x(n) = a(1)x(n-1) + a(2)x(n-2) + ... + a(k)x(n-k) ⎡ xx(0) xx(1) ... xx(k-1) ⎤ ⎡ a(0) ⎤ ⎡ xx(1) ⎤ ⎢ xx(1) xx(0) ... xx(k-2) ⎥ ⎢ a(1) ⎥ ⎢ xx(2) ⎥ ⎢ : : : ⎥ ⎢ : ⎥ = ⎢ : ⎥ ⎢ xx(k-2) xx(k-1) ... xx(1) ⎥ ⎢ a(k-1) ⎥ ⎢ xx(k-1) ⎥ ⎣ xx(k-1) xx(k-2) ... xx(0) ⎦ ⎣ a(k) ⎦ ⎣ xx(k) ⎦
Kalman filter
linear recurrence and linear time-invariant filter
遞迴數列可以作為濾波器的輸入。
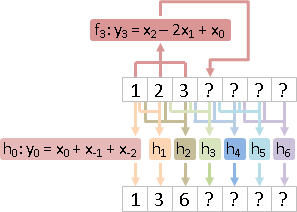
linear recurrence and linear time-invariant filter運算
resolution (Kalman filter): ⎰ f(?) = ? >> 1 , find x
⎱ h(?) = y
求解。求得原本遞迴數列。
Kalman filter
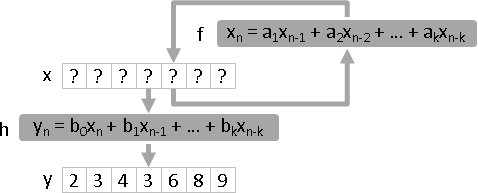
使用測量儀器h,時時收集數據y,時時推敲現況x。推定現況是自迴歸濾波器f,合乎自然規律。自創測量儀器是濾波器h,合乎電路原理。根據結果,推敲原因,此行為稱作「線性二次估計linear quadratic estimation」。
輸出誤差,通過反濾波器,得到輸入誤差,用以修正輸入。
為什麼要大費周章,將觀察值的誤差通過反濾波器,而不是直截了當,將觀察值通過反濾波器?我也不清楚。
h(x) = y
狀態 x₀ x₁ x₂ ... 未知(線性遞迴數列)
函數 h₀ h₁ h₂ ... 已知(數列每一項皆有一個函數)
觀察 y₀ y₁ y₂ ... 已知(數列每一項皆有一個輸出)
狀態是自迴歸的LTI filter xₙ = f(xₙ₋₁, xₙ₋₂, ..., xₙ₋ₖ)
xₙ = a₁xₙ₋₁ + a₂xₙ₋₂ + ... + aₚxₙ₋ₖ
函數可以一樣 h₀ = h₁ = h₂ = ...
函數可以推廣成LTI filter yₙ = hₙ(xₙ, xₙ₋₁, xₙ₋₂, ..., xₙ₋ₚ)
yₙ = bₙ₀xₙ + bₙ₁xₙ₋₁ + ... + bₙₚxₙ₋ₚ
從 x₁ 開始一個一個算到 xᵢ,現在要算 xᵢ 是多少:
1. x̂ᵢ = f(xᵢ₋₁) x 數列估計下一項。 (x₀ = 0)
此處以一階函數為例。
2. ŷᵢ = hᵢ(x̂ᵢ) y 數列估計下一項。
盜版 ŷᵢ 通常不等於正版 yᵢ。
這表示 x̂ᵢ 不夠準,需要修正。
3. kᵢ⁻¹ 求得誤差的反濾波器 kᵢ⁻¹。稱作Kalman gain。
kᵢ(x̂ᵢ - xᵢ) = (ŷᵢ - yᵢ)
(1) pᵢ = (x̂ᵢ - xᵢ)² 為了計算反濾波器,需要 xᵢ 的誤差的平方。
= cov(x̂ᵢ - xᵢ) 即是誤差的covariance。
sᵢ = (ŷᵢ - yᵢ)² 不過由於我們還沒求出 xᵢ,所以不能這樣算。
= cov(ŷᵢ - yᵢ)
(2) p̂ᵢ = f²(pᵢ₋₁) p 數列估計下一項。 (p₀ = 0)
= f pᵢ₋₁ fᵀ 原理是 Var[k⋅X] = k² ⋅ Var[X]。
(3) ŝᵢ = hᵢ²(p̂ᵢ) s 數列估計下一項。
= hᵢ p̂ᵢ hᵢᵀ 如果 f h 各有誤差項:常態分布 q r,平均數0。
那麼 p̂ᵢ ŝᵢ 各加上 var(q) var(r)。
(4) kᵢ⁻¹ = p̂ᵢ hᵢᵀ ŝᵢ⁻¹ 反濾波器是變異數的比值。這是什麼鬼啦?
4. xᵢ = x̂ᵢ - kᵢ⁻¹(ŷᵢ - yᵢ) 修正 x。
yᵢ 的誤差,通過反濾波器,還原成 xᵢ 的誤差。
x̂ᵢ 補上誤差,答案就對了。
5. pᵢ = p̂ᵢ - kᵢ⁻²(ŝᵢ) 修正 p。
= p̂ᵢ - kᵢ⁻¹ ŝᵢ kᵢ⁻¹ᵀ