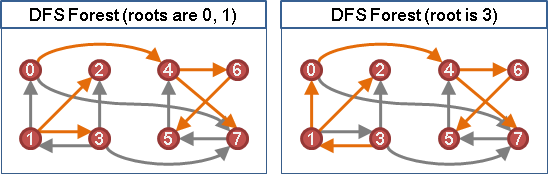
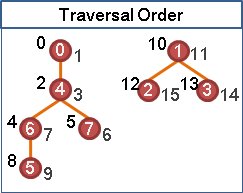
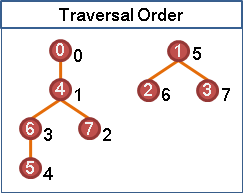
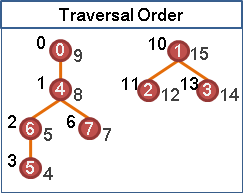
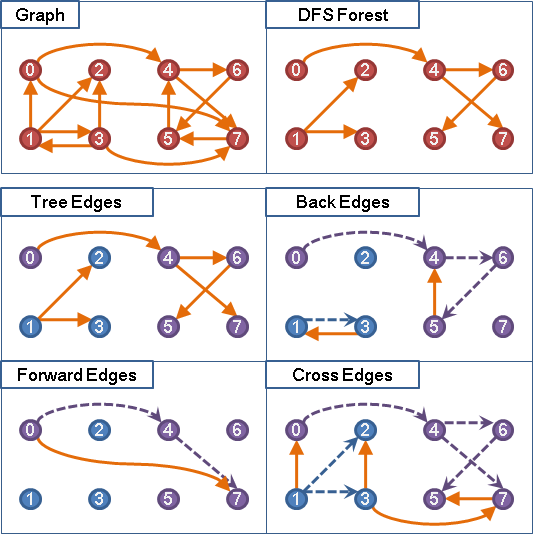
Graph

Graph中文翻做「圖」。此處談及的「圖」並不是指圖片或者圖形。「圖」是一種用來記錄關聯、關係的東西。

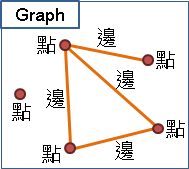
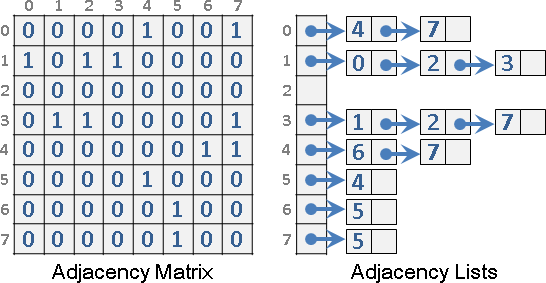
一張圖由數個點（vertex）以及數條邊（edge）所構成。點與點之間，得以邊相連接，表示這兩點有關聯、關係。

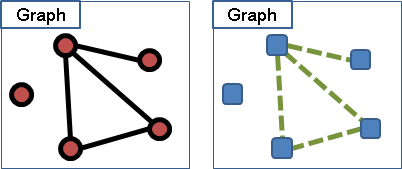
點的大小形狀和線的粗細長短是無所謂的，我們只在乎它們如何連接。只要連接的關係對了，要怎麼畫都行，簡約、雅觀、平易近人即可！

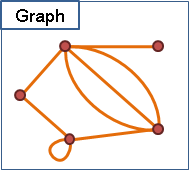
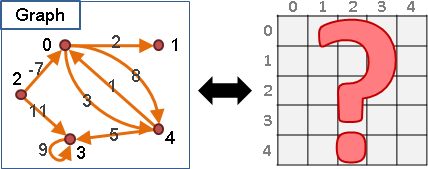
兩點之間也可以有很多條邊，甚至有自己連到自己的邊。兩點之間有很多條邊，代表這兩點有很多項關聯。一個點有自己連到自己的邊，表示自己和自己有項關聯。

Isomorphism / Isomorphic

Isomorphism中文譯作「同構」，Isomorphic中文譯作「同構的」。如果兩張圖的連接方式一模一樣時，則稱作「同構」。

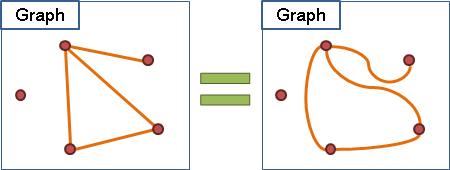
圖上的邊可以是直的，也可以是彎彎曲曲的，也可以是交錯的。不論邊的形狀如何，都不會改變點與點之間的關聯、關係，終究都會是同構的圖。

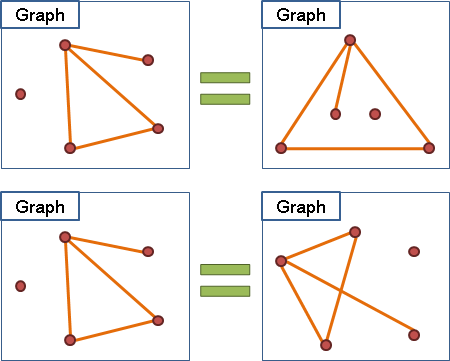
圖上的點可以任意移動位置。不論點的位置如何，都不會改變點與點之間的關聯、關係，終究都會是同構的圖。

同構的圖擁有相同的資訊，所以不管選擇哪一張圖都是可以的，只要清楚易懂就可以了！

Directed Graph（Digraph）

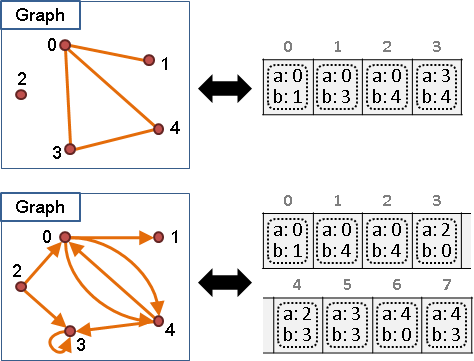
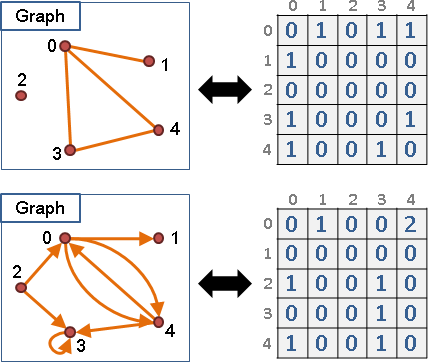
邊甚至可以擁有方向性，用來表示兩點間的關係是單向的，並非雙向的。無向邊代表雙向關係，有向邊代表單向關係。

一張圖若都是沒有方向性的邊，稱作「無向圖」；一張圖若都是有方向性的邊，則稱作「有向圖」。如果圖上有一些邊是單向的，有一些邊是雙向的，那我就不知道那該叫做什麼圖了。

替點和邊加上權重

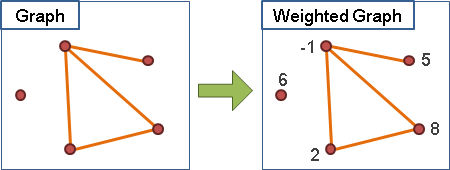
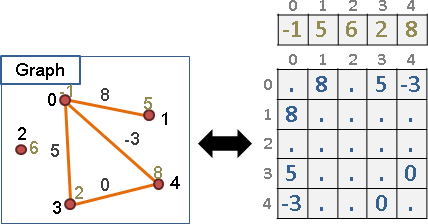
圖上的點可以擁有權重，可做其他用途。

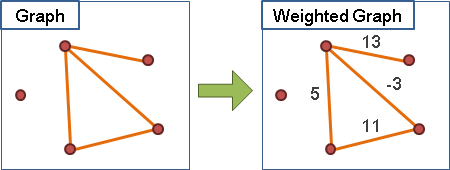
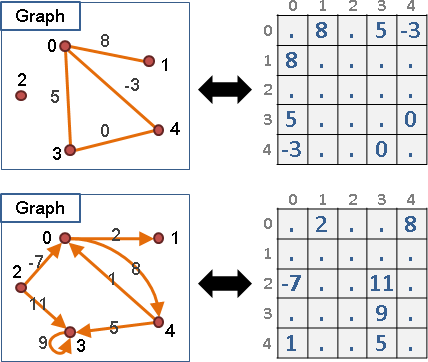
圖上的邊可以擁有權重，可做其他用途。

替點和邊取名字、代號

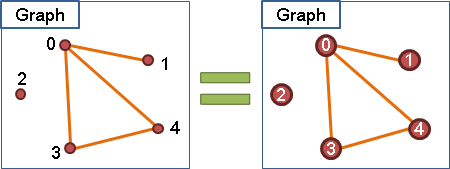
點和邊上面可以取名字、代號，方便辨認。名字、代號可以寫在點和邊的旁邊，也可以寫在點的裡面、邊的上面，只要能表達清楚就好。

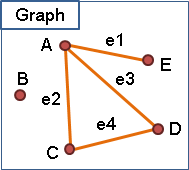
名字可以隨便取，簡單明瞭就好。書上通常是用英文字母及數字居多。

Edge List

來談談如何利用程式語言來儲存一張圖吧！

「邊表」。一條陣列，或者串列，記錄所有點與點之間的邊。

struct Edge { int a, b; // 一條邊的起點與終點 }; Edge edge[4]; // 四條邊 void edge_list() { int e = 0; // 邊數 int a, b; // 一條邊的端點、另一個端點 while (cin >> a >> b) { edge[e].a = a; edge[e].b = b; e++; } }

這種資料結構相當簡單直觀，也非常節省空間，卻不適合用於計算──無法迅速找到一個點碰觸的所有邊。

因此大家又發明了其他的方式，這裡介紹其中兩種最常見的方式：Adjacency Matrix、Adjacency Lists。adjacency為「相鄰」之意，以邊相連接的兩個點，則稱這兩個點「相鄰」。

Adjacency Matrix

「相鄰矩陣」。把一張圖上的點依序標示編號。然後建立一個方陣，記錄連接資訊。方陣中的每一個元素都代表著某兩點的連接資訊。例如元素(0,1)記錄著第0點到第1點的連接資訊、元素(4, 2)記錄著第4點到第2點的連接資訊。如此一來，任意兩個點之間的資訊，都有對應的地方可供記錄，纖悉無遺。

連接資訊可以是邊的數目，也可以是邊的權重，也可以儲存其他的資訊。

Adjacency matrix可以記錄邊的權重，但是無法記錄點的權重，也無法同時記錄點和邊的權重。不過呢，想要記錄點的權重，只需另外建立一條陣列，不是什麼難事。

另外，當兩點之間的邊超過一條的時候，Adjacency Matrix無法記錄權重。Adjacency Matrix的一個格子只能存入一個數字，無法同時存入多個數字。我們可以修改Adjacency Matrix的構造，以存入更多數字，只是這不在討論範圍之內，各位可自行研究。

int graph[5][5]; void adjacency_matrix() { for (int i=0; i<5; ++i) for (int j=0; j<5; ++j) graph[i][j] = 0; int a, b, w; // 一條邊的端點、另一個端點、邊的權重 while (cin >> a >> b >> w) graph[a][b] = w; }

Adjacency Lists

「相鄰列表」。把一張圖上的點依序標示編號。每一個點，後方列出所有相鄰的點。例如第4列是第4點所有相鄰的點。另外，相鄰的點也可以想成是相鄰的邊。

第一種，直覺的實作方式，採用陣列：

int list[5][100]; // 五個列表。每一個列表的相鄰邊數上限是100。 int size[5]; // 記錄每一個列表的元素有多少個 void adjacency_lists() { for (int i=0; i<5; ++i) size[i] = 0; int a, b; // 一條邊的端點、另一個端點 while (cin >> a >> b) list[a][size[a]++] = b; }

第二種，古板的實作方式，採用串列：

struct Element { int b; Element* next; }; Element* list[5]; // 五個列表 void add_edge(int a, int b) { Element* e = new Element(); e->b = b; e->next = list[a]; list[a] = e; } void adjacency_lists() { for (int i=0; i<5; ++i) list[i] = 0; int a, b; // 一條邊的起點、終點 while (cin >> a >> b) add_edge(a, b); }

第三種，輕鬆的實作方式，利用程式語言內建的vector或list：

vector<int> list[5]; void adjacency_lists() { for (int i=0; i<5; ++i) list[i].clear(); int a, b; // 一條邊的起點、終點 while (cin >> a >> b) list[a].push_back(b); }

如果還要記錄邊的權重，就變成這樣：

int list[5][100]; int weight[5][100]; // 再開一個陣列來記錄邊的權重 int size[5]; struct Element { int b, w; // 同時記錄邊的權重 Element* next; }; Element* list[5]; struct Element {int b, w;}; // 同時記錄邊的權重 vector<Element> list[5]; vector<pair<int,int>> list[5]; // 用pair作為b和w

如果還要記錄點的權重，那就另外再開一條陣列吧。

Adjacency Lists特殊的實作方式

中文網路俗稱「链式前向星」，命名品味令人嘆為觀止。

整併所有列表，置於一條陣列，或者一條串列。順序可以相間。

本質上還是Adjacency Lists，只不過是調整了實作方式。外觀上像是Edge List與Adjacency Lists兩者合體。

第四種，特殊的實作方式，記憶體取自陣列，不必new。

struct Element { int b, w; // 同時記錄邊的權重 int next; // 串列指標改成陣列索引值 }; int list[5]; // adjacency lists int e = 0; // 邊數 Element edge[100]; // edge list void add_edge(int a, int b, int w) { // 設定這條邊的起點、終點、權重 e->b = b; e->w = w; // 把邊插入到對應串列開頭 e->next = list[a]; list[a] = e; e++; } void adjacency_lists() { e = 0; for (int i=0; i<5; ++i) list[i] = -1; int a, b, w; // 一條邊的起點、終點、權重 while (cin >> a >> b >> w) add_edge(a, b, w); }

第五種，懶惰的實作方式，資料項目拆開成許多陣列。

int list[5]; int next[100], from[100], to[100], weight[100]; int e = 0; // 邊數 void add_edge(int a, int b, int w) { // 設定這條邊的起點、終點、權重 // from[e] = a; // 事實上不需要 to[e] = b; weight[e] = w; // 把邊插入到對應串列開頭 next[e] = list[a]; list[a] = e; e++; } void adjacency_lists() { e = 0; for (int i=0; i<5; ++i) list[i] = -1; int a, b, w; // 一條邊的起點、終點、權重 while (cin >> a >> b >> w) add_edge(a, b, w); }

Graph Traversal

給你一張圖，要怎麼讀出它的資訊呢？

用人眼來觀察一張圖，很快的就能看出點和線，一點一點釐清關係。要是一張圖能夠畫得漂亮一點，上個鮮明的顏色，那就更好了。

電腦則不然。要以電腦來讀取一張圖的資訊（這資訊想必會以圖的資料結構來妥善儲存），唯一的方法就是透過程式語言，以及良好的演算法囉！

Traversal中文稱作「遍歷」。圖的遍歷，也就是指通盤地讀取圖的資訊：決定好從哪裡開始讀，依照什麼順序讀，要讀到哪裡為止。詳細地設計好流程，始能通盤地讀取圖的資訊；如果設計得漂亮，在解決圖的問題時，還可以一邊讀取圖的資訊，一邊順手解決問題呢！

利用最簡單的資料結構queue和stack，就能製造不同的遍歷順序，得到兩種遍歷演算法：Breadth-first Search和Depth-first Search。這兩個演算法充分了利用程式語言的特性，簡約而美麗，成為資訊領域不可不知的演算法。

Breadth-first Search（BFS）

（依照編號順序）不斷找出尚未遍歷的點當作起點，進行下述行為：
　一、把起點塞入queue。
　二、重複下述兩步驟，直到queue裡面沒有東西為止：
　　甲、queue彈出一點。
　　乙、找出跟此點相鄰的點，並且尚未遍歷的點，
　　　　通通（依照編號順序）塞入queue。

教科書都有一步一步的示意圖，這裡不再重畫，只做額外補充。

運用BFS遍歷整張圖，最後得到許多棵樹。單一的樹稱作BFS Tree，所有的樹稱作BFS Forest。

不同的起點，形成不同的BFS Forest。我們習慣按照編號順序選擇下一個要拜訪的點，得到唯一一種BFS Forest。

遍歷順序示意圖：每個點進入與離開queue的時刻

每個點進入queue的時刻以左上深色數字表示，每個點離開queue的時刻以右下淺色數字表示。每個點都會進入queue一次、離開queue一次，不會再有第二次。

遍歷順序示意圖：每個點離開queue的時刻

只觀察離開queue的時刻，可以發現BFS優先走遍距離起點最近之處，優先讓BFS Tree變得寬廣，因而得名Breadth-first Search。這個遍歷順序能夠解決許多圖論問題！

時間複雜度

圖的資料結構為Adjacency Matrix是O(V²)；圖的資料結構為Adjacency Lists是O(V+E)。V是點數，E是邊數。

程式碼

bool adj[9][9]; // 一張圖，資料結構為adjacency matrix。 bool visit[9]; // 記錄圖上的點是否遍歷過，有遍歷過為true。 void BFS() { // 建立一個queue。 queue<int> q; // 全部的點都初始化為尚未遍歷 for (int i=0; i<9; i++) visit[i] = false; for (int k=0; k<9; k++) if (!visit[k]) { // 一、把起點塞入queue。 q.push(k); visit[k] = true; // 二、重複下述兩點，直到queue裡面沒有東西為止： while (!q.empty()) { // 甲、queue彈出一點。 int i = q.front(); q.pop(); // 乙、找出跟此點相鄰的點，並且尚未遍歷的點， // 依照編號順序通通塞入queue。 for (int j=0; j<9; j++) if (adj[i][j] && !visit[j]) { q.push(j); visit[j] = true; } } } } // 很差的寫法，點從queue彈出之後才設定遍歷過了。 bool adj[9][9]; bool visit[9]; void BFS() { queue<int> q; for (int i=0; i<9; i++) visit[i] = false; for (int k=0; k<9; k++) if (!visit[k]) { q.push(k); while (!q.empty()) { int i = q.front(); q.pop(); if (!visit[i]) { visit[i] = true; for (int j=0; j<9; j++) if (adj[i][j] && !visit[j]) q.push(j); } } } }

Depth-first Search（DFS）

DFS與BFS大同小異，只是把queue換成了stack而已。

遍歷順序示意圖：每個點進入與離開stack的時刻

每個點進入stack的時刻以左上深色數字表示，每個點離開stack的時刻以右下淺色數字表示。每個點都會進入stack一次、離開stack一次，不會再有第二次。

遍歷順序示意圖：每個點離開stack的時刻

只觀察離開stack的時刻，可以發現DFS優先走遍距離起點最遠之處，優先讓DFS Tree變得深遠，因而得名Depth-first Search。這個遍歷順序能夠解決許多圖論問題！

遞迴版本程式碼

DFS的程式碼也可以寫成遞迴形式。程式語言中的遞迴，其實就是利用stack來實作的。

bool adj[9][9]; // 一張圖，資料結構為adjacency matrix。 bool visit[9]; // 記錄圖上的點是否遍歷過，有遍歷過為true。 void DFS(int i) { for (int j=0; j<9; j++) if (adj[i][j] && !visit[j]) { visit[j] = true; // 標記為已遍歷 DFS(j); } } void traversal() { // 全部的點都初始化為尚未遍歷 for (int i=0; i<9; i++) visit[i] = false; for (int i=0; i<9; i++) if (!visit[i]) { visit[i] = true; DFS(i); } } bool adj[9][9]; bool visit[9]; void DFS(int i) { visit[i] = true; for (int j=0; j<9; j++) if (adj[i][j] && !visit[j]) DFS(j); } void traversal() { for (int i=0; i<9; i++) visit[i] = false; for (int i=0; i<9; i++) if (!visit[i]) DFS(i); } bool adj[9][9]; bool visit[9]; void DFS(int i) { if (visit[i]) return; visit[i] = true; for (int j=0; j<9; j++) if (adj[i][j]) DFS(j); } void traversal() { for (int i=0; i<9; i++) visit[i] = false; for (int i=0; i<9; i++) DFS(i); }

遍歷順序示意圖：每個點進入遞迴與離開遞迴的時刻

進入遞迴的時刻以左上深色數字表示，離開遞迴的時刻以右下淺色數字表示。這個順序用於解決一些特別的圖論問題。

製圖時，DFS Tree高度至少是三、分枝數目至少是三，比較容易觀察出遍歷順序。建議讀者也自己畫個圖、寫段程式研究一下。

邊的分類

藉由一叢DFS Forest，一張有向圖的邊可以分成四類：

Tree Edge：樹上的邊。
Back Edge：連向祖先的邊。（形成環）
Forward Edge：連向子孫的邊。
Cross Edge：枝葉之間的邊、樹之間的邊。（可能形成環）

藉由一叢DFS Forest，一張無向圖的邊可以分成兩類：

Tree Edge：樹上的邊。
Back Edge：連向祖先的邊。（形成環）

這些邊的分類，可以協助我們解決複雜的圖論問題。

d[x] : 節點 x 進入遞迴的時刻
f[x] : 節點 x 離開遞迴的時刻
(i,j) is a tree edge or a forward edge : d[i] < d[j] < f[j] < f[i]
(i,j) is a back edge : d[j] < d[i] < f[i] < f[j]
(i,j) is a cross edge : d[j] < f[j] < d[i] < f[i]