第 4 章其他主題

4.1 維度 T 的異質性-雙維模型

Two-way error component regression
雙維效果考慮時間的期間效果(Period Effects)，Error component 展開的方程式如下： \[ {{Y}_{it}} = a+\sum\limits_{\kappa =1}^{K}{{{b}_{\kappa }}{{X}_{\kappa it}}}+{{u}_{it}} \\ {{u}_{it}} ={{\mu }_{i}}+{{\lambda }_{t}}+{{v}_{it}} \] $\lambda_t$即為期間效果向量。有多少的 $T$ ，就有幾個值。估計 $\lambda_t$ 即為期間效果向量的期間效果資料如圖4.1，其實就是期間的虛擬數，概念就是期間啞變數。

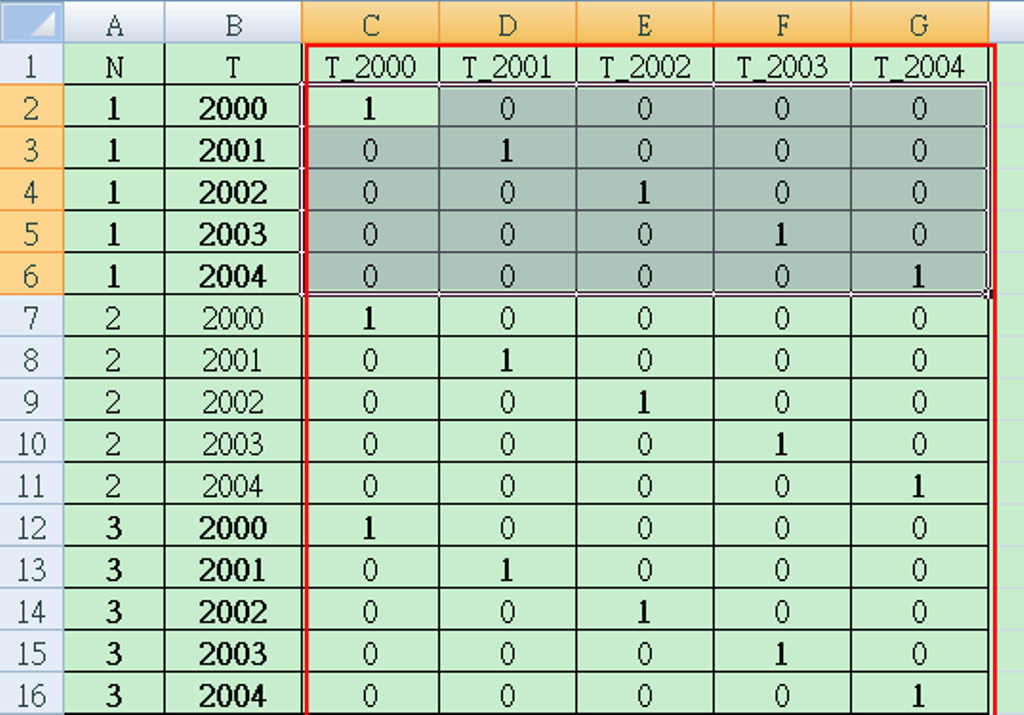
圖 4.1: 期間的虛擬數

估計上和前面一樣， $\lambda_t$ 可以是固定效果，也可以是隨機效果；基本上和橫斷面效果 $\mu_i$ 假設一樣，雙維模型是一個相當有彈性的模型設計。 $N$ 方向的單維設定是Panel Data 的基本架構，也就是因為這樣，其漸進性質才能夠由 $N \to \infty$ 的方式去證明。但是，何時須要增加第二維的期間效果？針對這個問，有兩個方法論的哲學：第1、統計意義。由假設檢定的角度來決定，看看likelihood ratio對於單維和雙維的看法如何。如果雙維的概似值最好，那就使用雙維。
第2、實證意義。例如，如果是經濟性質的資料，由資料期間的經濟活動的特徵來看，如果資料期間發生某些共同事件，影響了所有 $N$ 在某一些時間產生共同的行為，例如，2008年金融海嘯以及其引發的經濟危機，這一年，幾乎絕大多數的國家或公司的表現，都會一致的低於平均。所以，出現了 $N$ 在「特定時間的共同行為」。這樣，將模型增加為雙維效果是一個合理的做法。類似因素包括「全球廣告的傳播效果」和「景氣循環」等等，都具有這樣的特徵。如果是政治性質的資料，也可以用類似的角度去審視資料。
雖然在實證意義上，單獨的期間效果不是很合宜，但是，許多商業軟體都可以獨立宣告，例如 Stata和 Eviews等等。我們看R的例子：

估計固定效果之單維時間效果:

library(plm)
gsp_fe_t = plm(Eq,effect = "time", model = "within", data = myData1)
summary(gsp_fe_t)

## Oneway (time) effect Within Model
## 
## Call:
## plm(formula = Eq, data = myData1, effect = "time", model = "within")
## 
## Balanced Panel: n = 48, T = 17, N = 816
## 
## Residuals:
##       Min.    1st Qu.     Median    3rd Qu.       Max. 
## -0.2273588 -0.0542245 -0.0074907  0.0490690  0.3431431 
## 
## Coefficients:
##              Estimate Std. Error t-value  Pr(>|t|)    
## x1_hwy      0.0637374  0.0162850  3.9139 9.863e-05 ***
## x2_water    0.1162447  0.0124961  9.3024 < 2.2e-16 ***
## x3_other    0.0110788  0.0123861  0.8945  0.371352    
## x4_private  0.3085830  0.0115863 26.6335 < 2.2e-16 ***
## x5_emp      0.5478729  0.0155024 35.3412 < 2.2e-16 ***
## x6_unemp   -0.0055691  0.0017245 -3.2294  0.001292 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Total Sum of Squares:    834.46
## Residual Sum of Squares: 5.7175
## R-Squared:      0.99315
## Adj. R-Squared: 0.99296
## F-statistic: 19157.3 on 6 and 793 DF, p-value: < 2.22e-16

估計雙維固定效果:

gsp_fe_2 = plm(Eq, effect ="twoways", model = "within", data = myData1)
summary(gsp_fe_2)

## Twoways effects Within Model
## 
## Call:
## plm(formula = Eq, data = myData1, effect = "twoways", model = "within")
## 
## Balanced Panel: n = 48, T = 17, N = 816
## 
## Residuals:
##        Min.     1st Qu.      Median     3rd Qu.        Max. 
## -0.15870926 -0.01840671 -0.00088238  0.01659933  0.16463951 
## 
## Coefficients:
##              Estimate Std. Error t-value  Pr(>|t|)    
## x1_hwy      0.0616918  0.0306734  2.0112 0.0446587 *  
## x2_water    0.0417471  0.0153776  2.7148 0.0067848 ** 
## x3_other   -0.0946841  0.0168626 -5.6150 2.773e-08 ***
## x4_private  0.1571906  0.0273426  5.7489 1.309e-08 ***
## x5_emp      0.8052784  0.0283776 28.3772 < 2.2e-16 ***
## x6_unemp   -0.0039595  0.0011802 -3.3550 0.0008337 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Total Sum of Squares:    3.5892
## Residual Sum of Squares: 0.84111
## R-Squared:      0.76565
## Adj. R-Squared: 0.74398
## F-statistic: 406.221 on 6 and 746 DF, p-value: < 2.22e-16

effect 有三種效果: “individual”, “time”, 和” twoways “。不特別指定時，內定是”individual”。

接下來，我們分析且比較MLE和GLS的雙維隨機效果，要注意雙維效果宣告方式有random=~1|state/year和 random=~1|state|year兩種，且這兩種是不同的。

random=~1|state/year是panel data的雙維。
random=~1|state|year則是巢式(Nested)關係，或階層式。

MLE的雙維隨機效果，R Code Chunk與估計結果如下：

gsp_reML=nlme::lme(as.formula(Eq),data=temp1,random=~1|state/year)
summary(gsp_reML)

## Linear mixed-effects model fit by REML
##   Data: temp1 
##        AIC       BIC   logLik
##   -2785.69 -2738.732 1402.845
## 
## Random effects:
##  Formula: ~1 | state
##         (Intercept)
## StdDev:  0.08987078
## 
##  Formula: ~1 | year %in% state
##         (Intercept)   Residual
## StdDev:   0.0328234 0.01665908
## 
## Fixed effects:  as.formula(Eq) 
##                  Value  Std.Error  DF   t-value p-value
## (Intercept)  2.1783595 0.14938903 762 14.581790  0.0000
## x1_hwy       0.0628585 0.02292175 762  2.742307  0.0062
## x2_water     0.0754364 0.01404131 762  5.372463  0.0000
## x3_other    -0.1009956 0.01716109 762 -5.885150  0.0000
## x4_private   0.2693669 0.02085568 762 12.915757  0.0000
## x5_emp       0.7557325 0.02577602 762 29.319215  0.0000
## x6_unemp    -0.0057849 0.00089791 762 -6.442619  0.0000
##  Correlation: 
##            (Intr) x1_hwy x2_wtr x3_thr x4_prv x5_emp
## x1_hwy     -0.729                                   
## x2_water    0.168  0.016                            
## x3_other    0.012 -0.364 -0.142                     
## x4_private -0.502 -0.027 -0.336  0.051              
## x5_emp      0.494 -0.196 -0.217 -0.401 -0.606       
## x6_unemp    0.424 -0.142 -0.143 -0.222 -0.399  0.534
## 
## Standardized Within-Group Residuals:
##         Min          Q1         Med          Q3         Max 
## -1.44662207 -0.28147969 -0.01784047  0.22036250  1.87991320 
## 
## Number of Observations: 816
## Number of Groups: 
##           state year %in% state 
##              48             816

取出橫斷面 $N$ 的隨機效果估計值，這個是 $N \times 1$ 的向量。

summary(gsp_reML)$coef$random$state

##      (Intercept)
## 1  -0.1308619791
## 2   0.0387526324
## 3  -0.0303404760
## 4   0.1106973736
## 5   0.0363469261
## 6   0.1001033220
## 7   0.1391623627
## 8  -0.0322155953
## 9  -0.0738272598
## 10  0.0322607008
## 11  0.0047075227
## 12 -0.0772453994
## 13 -0.0528459034
## 14 -0.0193152914
## 15  0.0186416659
## 16  0.1554067985
## 17 -0.1019342134
## 18  0.0105125814
## 19  0.0489672821
## 20  0.0103173548
## 21 -0.0729269796
## 22 -0.0686854287
## 23 -0.0540234100
## 24 -0.0241390141
## 25  0.0138338880
## 26  0.0185932878
## 27 -0.0157457892
## 28  0.0684231351
## 29  0.1087596279
## 30  0.1166637061
## 31 -0.1144385293
## 32 -0.0009390054
## 33 -0.0826019103
## 34  0.0786537035
## 35 -0.0206257253
## 36 -0.0852076162
## 37  0.0492616634
## 38 -0.2029098258
## 39 -0.0519998692
## 40 -0.1342784044
## 41 -0.0015866501
## 42  0.0335657403
## 43 -0.0208707644
## 44 -0.0240216436
## 45  0.1140526477
## 46 -0.0550368343
## 47 -0.0521666751
## 48  0.2931062702

取出期間 $T$ 的隨機效果估計值。這個是 $N \times (T-1) \times 1$ 的向量。我們簡單檢視前6筆即可

head(summary(gsp_reML)$coef$random$year)

##        (Intercept)
## 1/1970 -0.04557345
## 1/1971 -0.03352921
## 1/1972 -0.02261967
## 1/1973 -0.01248458
## 1/1974 -0.02336189
## 1/1975 -0.01566725

plm 的GLS和 lme 的MLE兩個方法，所估計的雙維隨機效果，結果有何差異？

gsp_re_2=plm(Eq, effect ="twoways", model = "random", data = myData1)
summary(gsp_re_2)$coef

##                 Estimate  Std. Error   z-value      Pr(>|z|)
## (Intercept)  2.317338907 0.145109940 15.969539  2.083186e-57
## x1_hwy       0.074011216 0.023339302  3.171098  1.518639e-03
## x2_water     0.062040446 0.013706898  4.526221  6.004782e-06
## x3_other    -0.090290383 0.016281121 -5.545710  2.927630e-08
## x4_private   0.239945982 0.020945038 11.455982  2.194608e-30
## x5_emp       0.766065523 0.024458921 31.320496 2.454676e-215
## x6_unemp    -0.004482513 0.001000356 -4.480917  7.432298e-06

summary(gsp_reML)$tTable

##                    Value    Std.Error  DF   t-value       p-value
## (Intercept)  2.178359517 0.1493890339 762 14.581790  1.165581e-42
## x1_hwy       0.062858470 0.0229217481 762  2.742307  6.244089e-03
## x2_water     0.075436432 0.0140413115 762  5.372463  1.032747e-07
## x3_other    -0.100995609 0.0171610925 762 -5.885150  5.956589e-09
## x4_private   0.269366853 0.0208556766 762 12.915757  1.187408e-34
## x5_emp       0.755732527 0.0257760153 762 29.319215 4.292906e-127
## x6_unemp    -0.005784884 0.0008979088 762 -6.442619  2.080133e-10

比較兩個結果，估計值的差異並不大，但是和固定效果比較時，就會發現關鍵就是效果設定。固定效果的 $x3$ 係數不顯著且為正，與此相異甚大。因此，誰是正確的以及如何正確估計出參數，都是實證上困難的問題。
最後，不管是單維或雙維，我們想知道估計出來的固定效果有多大？數字為何？等問題，plm內有萃取函數fixef(object, effect=)，以雙維為例的程式語法如下：

FE=fixef(gsp_fe_2, effect= "individual")
PE=fixef(gsp_fe_2, effect= "time")

接下來將固定效果FE轉換成矩陣，可和前面比較。

head(as.matrix(FE))

##       [,1]
## 1 3.065845
## 2 3.209156
## 3 3.102565
## 4 3.459024
## 5 3.223504
## 6 3.257311

將期間效果賦予時間框架後，畫圖顯示，如圖4.2。

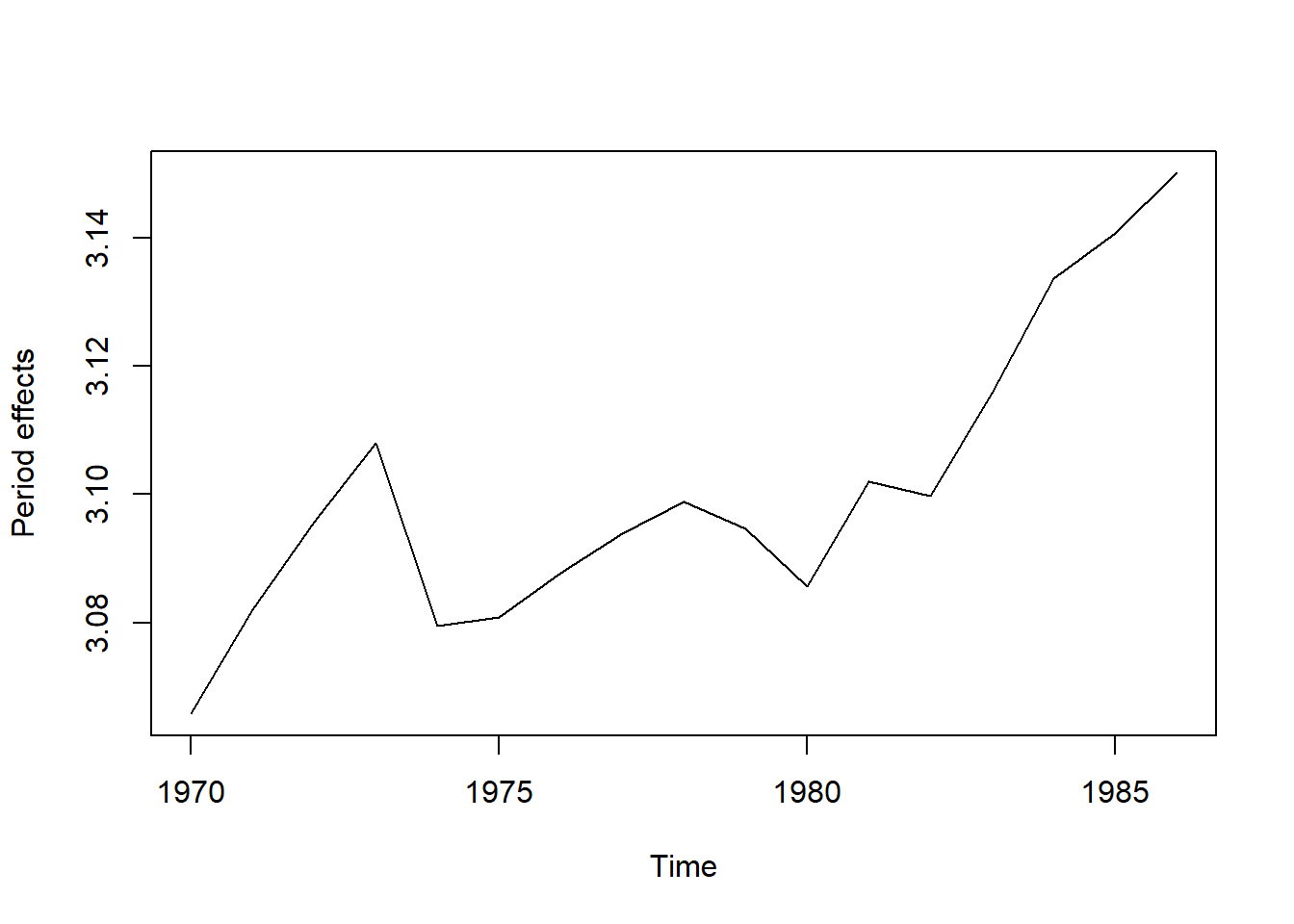
圖 4.2: 期間效果時間序列

4.2 變動係數 (variable coefficients models)

傳統上的panel data 除了本書主要提到的共同係數之外，還有變動係數模型(variable coefficients models, VCM)。這樣的模式和Peseran的CCE很像，只是沒有處理橫段面相依。因為本章一開始的介紹，會使許多讀者覺得CCE和變動係數模型很像。在panel data econometrics中，因為VCM估計上相當繁瑣，幾乎很少被注意，也不是很主要的方法。理論的介紹，目前就筆者所知是 Hsiao (2003) ³和 Greene (2012) 第11章第11節。其餘如Baltagi和Wooldridge的專書，都沒有專章在介紹。
但是，如同 Hsiao (2003) ⁴ 所提到的，雖然Variable Coefficient沒有吸引多數計量學者的注意，但是，很多經濟模型都必須在一個Panel整體下，考慮合理的變動係數模型。例如，經濟成長函數的跨國研究，沒有理論認為非洲國家人力資本對經濟成長的邊際效果和英美等國是一樣的。一個簡單的方法就是再用一次LSDV的技巧於解釋變數，整個解釋變數矩陣，就會再次被擴大。
因為這個模型代數結構的符號過於繁瑣，這一節，就不花篇幅介紹這個模型的代數結構，有興趣的讀者請參考 Hsiao (2003) 第6章。我們直接看plm的pvcm()函數和程式。
下例我們利用資料retVol.csv，這是取550家上海證交所上市公司的日資料，換算成月資訊資料。
被解釋變數：月平均報酬(RET)；
解釋變數：月的標準差(STD)，以及交易量(VOLUMN)。

這樣的迴歸，理論上的預期都是正相關：(1)標準差越大，預期報酬越高；(2)交易量越大，報酬也越高。
這是不平衡資料，550家公司，從43個月到113個月都有，總資料樣數為N=55232筆。
估計Variable Coefficients Model 的R Code如下：

tempx = read.csv("data/retVol.csv")
DataVC= pdata.frame(tempx, index = c("ID","DATEID"))
myFormVC=RET ~ STD + log(VOLUMN)
pvcm_FE = pvcm(myFormVC, data = DataVC, model = "within")

函數pvcm()可以接受固定效果含隨機效果。這也是VCM的一個好處。因為它處理係數和個別效果時，會個別去處理變動係數，這樣反而讓估計過程簡易化。從上述估計結果摘要可以看出，因為是隨$N$的變動係數，所以，摘要時就只能做了係數的基礎分配摘要。

summary(pvcm_FE)

## Oneway (individual) effect No-pooling model
## 
## Call:
## pvcm(formula = myFormVC, data = DataVC, model = "within")
## 
## Unbalanced Panel: n = 550, T = 43-113, N = 55232
## 
## Residuals:
##         Min.      1st Qu.       Median      3rd Qu.         Max. 
## -116.1135589   -7.0909463    0.3178142    7.4159293   95.0884109 
## 
## Coefficients:
##   (Intercept)          STD           log(VOLUMN)    
##  Min.   :-75.87   Min.   :-9.2019   Min.   :-4.103  
##  1st Qu.:-33.15   1st Qu.:-2.6949   1st Qu.: 2.751  
##  Median :-24.40   Median :-1.6494   Median : 4.065  
##  Mean   :-26.64   Mean   :-1.5361   Mean   : 4.191  
##  3rd Qu.:-17.41   3rd Qu.:-0.4689   3rd Qu.: 5.330  
##  Max.   : 41.86   Max.   : 6.2437   Max.   :12.321  
## 
## Total Sum of Squares: 12292000
## Residual Sum of Squares: 9652700
## Multiple R-Squared: 0.21471

隨機效果則如下。因為隨機效果之VCM是由常態分配取出，所以也稱為隨機係數模式Random Coefficient Model。估計結果是現出平均值。承上例的隨機效果VCM如下：

pvcm_RE = pvcm(myFormVC, data = DataVC, model = "random")
summary(pvcm_RE)

## Oneway (individual) effect Random coefficients model
## 
## Call:
## pvcm(formula = myFormVC, data = DataVC, model = "random")
## 
## Unbalanced Panel: n = 550, T = 43-113, N = 55232
## 
## Residuals:
##       Min.    1st Qu.     Median       Mean    3rd Qu.       Max. 
## -128.37556   -7.54859    0.14542   -0.08372    7.71504  119.43468 
## 
## Estimated mean of the coefficients:
##               Estimate Std. Error z-value  Pr(>|z|)    
## (Intercept) -22.151724   0.545055 -40.641 < 2.2e-16 ***
## STD          -1.327587   0.066874 -19.852 < 2.2e-16 ***
## log(VOLUMN)   3.540540   0.079351  44.619 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Estimated variance of the coefficients:
##             (Intercept)      STD log(VOLUMN)
## (Intercept)     91.5131  3.29317   -11.76061
## STD              3.2932  0.64121    -0.66674
## log(VOLUMN)    -11.7606 -0.66674     1.75241
## 
## Total Sum of Squares: 12292000
## Residual Sum of Squares: 10369000
## Multiple R-Squared: 0.15644
## Chisq: 2049.88 on 2 DF, p-value: < 2.22e-16

如果想要看全部，就用summary(pvcm_FE)$coef。下面以2個係數為例，顯示部份公司。

summary(pvcm_FE)$coef[,2:3]

##                 STD log(VOLUMN)
## 600000 -0.976991459   2.1897837
## 600001  0.957988607   1.1484744
## 600002  0.844075464   3.7588955
## 600003 -2.138944329   4.1618985
## 600004  0.105858318   6.0168728
## 600005  0.124510859   0.9649056
## 600006 -2.172576445   4.3795751
## 600007 -1.085361239   4.3014305
## 600008 -3.230563077   4.3437427
## 600009 -1.609990044   2.4672727
## 600010  0.337159703   1.8029281
## 600011 -0.323213604   1.9155788
## 600012 -1.183125839   4.3563269
## 600015 -2.110491709   7.2350681
## 600016  0.453486047   1.1795015
## 600017 -1.015910359   4.7179472
## 600018  1.215890724   7.0195544
## 600019 -0.708966851   2.4584286
## 600020 -0.953743374   4.4769032
## 600021 -1.575493367   5.6098167
## 600022  0.823391336   2.1326616
## 600026 -2.373596207   6.8395267
## 600027 -1.568588301   7.7678481
## 600028 -2.650990642   5.4387913
## 600029 -1.644115434   7.0597498
## 600030  2.342928287   1.1357755
## 600031  2.301215489   1.4380035
## 600033 -1.056458674   1.6067834
## 600035 -2.438190046   5.1131004
## 600036 -0.768651770   3.5421968
## 600037 -2.341270710   2.1532282
## 600038  0.493656431   2.4261379
## 600039 -2.233181411   4.7310970
## 600048 -0.017840407  -4.1027742
## 600050 -0.726098323   5.7014493
## 600051 -2.021802319   4.0035923
## 600052 -4.651285472   6.3185288
## 600053 -1.775760731   6.7952895
## 600054 -0.891516675   2.2155211
## 600055 -0.244150010   4.9677077
## 600056 -1.528421149   4.1083748
## 600057 -2.923287579   6.7405383
## 600058  0.436680933   2.3119510
## 600059 -1.841046253   2.6361896
## 600060 -2.842265737   6.3599362
## 600061 -2.188519481   4.5793564
## 600062 -2.137062909   4.4669101
## 600063 -1.097499145   4.2275003
## 600064 -3.024087527   5.5195404
## 600066 -0.122696167   2.5966546
## 600067 -1.382912189   2.9040669
## 600068  0.495043109   2.6146704
## 600069 -3.034854134   5.9346970
## 600070 -2.722319299   3.8743414
## 600071 -4.115176107   7.6861273
## 600072  0.287921189   8.1347651
## 600073 -1.761717309   5.6597879
## 600074 -2.243875446   2.9084652
## 600075 -2.620249961   3.6388628
## 600076 -3.257504036   7.0421656
## 600077 -2.048460460   4.4465310
## 600078 -3.596404634   3.0312690
## 600079 -1.287892934   4.4144536
## 600080 -2.091921933   3.5303174
## 600081 -1.654770227   3.3009262
## 600082 -0.453260419   3.0447916
## 600083  1.761016652   7.3741866
## 600084  0.687675994   2.6746608
## 600085  0.252149975   1.1934425
## 600086 -3.242356377   5.9135516
## 600087 -1.662333648   2.1897798
## 600088 -2.938748466   5.5082300
## 600089  0.637327836   1.1771041
## 600090 -6.672574650   7.6567579
## 600091 -2.768549889   4.5317224
## 600093 -0.528371989   2.4908540
## 600094  2.310084693   2.2413539
## 600095 -1.440457344   3.2436765
## 600096 -1.196389358   1.0529871
## 600097 -1.692862164   5.4538044
## 600098 -1.484156732   3.9426838
## 600099 -2.845623461   8.7368383
## 600100  0.635949252   3.3744624
## 600101 -3.457464541   3.2645760
## 600102 -2.220375171   4.5260649
## 600103 -1.000385327   3.4249669
## 600104 -0.645191609   6.4256939
## 600105 -3.512858121   4.8104277
## 600106  0.283823580   2.4784681
## 600107 -1.169202777   3.1979548
## 600108 -2.041474135   3.2135771
## 600109  1.149369729   1.2048989
## 600110  0.069894845   2.1947310
## 600111  0.299209400   3.2148721
## 600112  0.126168310   3.1852417
## 600113 -2.928178599   4.1782985
## 600114 -2.892793765   5.2065478
## 600115 -1.903717911   6.1255878
## 600116 -1.795824745   4.9314916
## 600117 -1.614554212   4.3705740
## 600118 -2.400377492   4.1490698
## 600119 -3.229970377   4.2853068
## 600120 -2.135003491   4.9687588
## 600121 -2.878778103   4.2433010
## 600122 -2.119220418   5.7372079
## 600123 -2.851007000   4.7399429
## 600125 -0.435276741   2.3282317
## 600126 -0.990526937   2.8795666
## 600127  0.192982621   2.8084026
## 600128 -2.010190246   3.4254725
## 600129 -2.765635194   4.7518340
## 600130 -1.822535427   2.5855235
## 600131 -2.169584267   3.1735077
## 600132 -0.627374371   2.8925124
## 600133 -2.148145154   4.5496163
## 600135 -5.296053412   9.1406786
## 600136 -3.080643182   4.8950039
## 600137 -0.593821810   2.6283666
## 600138 -2.436731999   3.5519269
## 600139 -2.136360734   5.7910443
## 600141 -2.915385863   4.1351524
## 600143 -0.558777066   0.4632841
## 600145 -1.436847152   4.6861973
## 600146 -4.292300733   9.0532127
## 600148 -2.745653196   4.9114889
## 600149 -4.275378627   6.2775770
## 600150  2.087451585   0.9130276
## 600151  0.197204398   3.4181400
## 600152 -2.305086120   4.4861385
## 600153 -1.214767880   3.6137195
## 600155  0.970888630   1.9953256
## 600156 -1.017368677   4.9378269
## 600157 -3.730834082   4.5947683
## 600158  0.608684659   0.4158816
## 600159 -2.225300895   4.0633041
## 600160 -3.184531274   4.3114317
## 600161  0.789183753   2.2699863
## 600162 -2.322983752   4.4209781
## 600163 -1.963169406   2.5690438
## 600165 -4.448860276   9.5220998
## 600166 -0.257953285   3.7518704
## 600167 -2.990920823   8.4118784
## 600168 -3.060522566   4.7190486
## 600169  0.918254693   4.5323475
## 600170 -2.117964076   4.7504968
## 600171 -2.053066283   4.2336924
## 600172 -4.560103710   4.5767207
## 600173 -4.218349927   7.4584159
## 600175 -3.749058220   5.5469347
## 600176 -0.415117292   2.7499541
## 600177 -0.056070102   2.3712140
## 600178 -3.023025157   4.7806659
## 600179 -2.045683574   3.2898069
## 600180 -0.825589370  -0.2036696
## 600182 -1.149629388   7.7628890
## 600183 -2.942361868   3.9430619
## 600184  0.441554103   7.1593602
## 600185 -1.126158152   3.7990624
## 600186 -3.638879142   4.2791023
## 600187 -2.319370045   3.0420055
## 600188 -3.033112473   4.5627744
## 600189 -2.610441576   3.8054202
## 600190  0.423352945   3.4851941
## 600191 -1.165670537   3.8841716
## 600192 -2.076534526   5.0060162
## 600193 -1.155177401   4.0834239
## 600195 -1.032879810   4.5283741
## 600196 -1.336991726   3.2672474
## 600197 -1.957924255   3.7527647
## 600198 -1.341825048   7.6676508
## 600199 -4.481682864   6.5840752
## 600200 -3.530001497   3.0524844
## 600201 -1.949378329   2.8563950
## 600202  1.837815599   2.2007535
## 600203 -2.496206069   3.7938528
## 600206 -1.217358968   3.0813553
## 600207 -0.344669226   7.9290390
## 600208 -0.954892657   2.4996323
## 600209 -0.454101779   5.2703308
## 600210 -1.000071292   1.8535794
## 600211 -4.052442944   5.1394498
## 600212 -1.910557723   2.9645328
## 600213 -3.727838061   5.4154356
## 600215 -1.883755766   3.9207917
## 600216  0.052406430   3.2591461
## 600217  0.350389257   0.7199141
## 600218 -2.700355227   5.2962917
## 600219 -1.036982801   2.1517002
## 600220  1.369808261   1.0264353
## 600221 -3.150317437   5.0563787
## 600222 -1.776684096   2.0065062
## 600223  0.068726705   4.3680186
## 600225 -0.112759209   4.9362870
## 600226 -2.245257923   3.5870113
## 600227 -3.050068331   2.5752772
## 600228 -4.887392741   7.7507822
## 600229 -2.420609835   3.3211767
## 600230 -1.953503247   5.0318851
## 600231  0.017272184   2.4983401
## 600232 -2.703863619   3.0207976
## 600233 -2.505927914   5.0936256
## 600234 -4.750182362   6.7397719
## 600235 -2.376576407   3.2421559
## 600236 -1.094137166   2.2404132
## 600237 -1.879288734   3.0551158
## 600238 -3.997208495   6.0129526
## 600239  1.187668582   1.3961756
## 600240  0.655407593   1.3652432
## 600241 -2.648140976   4.9463602
## 600242 -0.942662293   5.3749663
## 600243 -2.914171695   5.3188573
## 600246  1.616533282   1.0251208
## 600247 -0.973282163   2.5864965
## 600248 -1.791597541   4.5215942
## 600249  0.737823456   1.6560420
## 600250 -1.126322263   3.5049150
## 600251  2.314046622   3.7747309
## 600252 -1.632713000   6.2379782
## 600253 -1.913758893   4.7722813
## 600255 -0.849957173   2.0398381
## 600256 -2.145339902   4.0502202
## 600257 -0.276523763   1.6802344
## 600258 -3.104697781   5.3604195
## 600259 -0.656618905   8.4105310
## 600260 -1.522184833   3.0581450
## 600261 -2.268950884   3.8077507
## 600262 -3.183047770   4.8527776
## 600263 -3.586306380   6.7376466
## 600265 -0.600082773   2.9243921
## 600266 -1.706797574   3.7512414
## 600267 -0.846351388   3.5228170
## 600268 -1.774000985   3.9863834
## 600269 -1.035754131   1.7916949
## 600270 -2.427244512   3.0202088
## 600271  0.620925449   0.4027998
## 600272 -0.682906616   1.7306925
## 600273 -2.354862620  10.3620503
## 600275 -1.109354943   4.0609370
## 600276  1.091232439   2.9463326
## 600277 -2.760487532   4.7430521
## 600278 -1.867118923   4.2495292
## 600279 -1.122883646   5.0480231
## 600280 -2.451747603   5.6639315
## 600281 -3.656755449   5.8547767
## 600282 -0.047809901   3.1796459
## 600283 -2.392729992   3.7098258
## 600284 -0.466612296   4.8532469
## 600285 -0.911541248   2.9995230
## 600287 -1.740761842   4.2243528
## 600288 -2.757059714   3.2420884
## 600289 -2.306318895   2.4901753
## 600290  1.174587432   0.7220408
## 600291  0.054495833   3.0543803
## 600292 -2.483526849   4.7290012
## 600293 -3.981653694   5.5376830
## 600295 -2.759388081   4.5880125
## 600297 -0.290824631   2.3220157
## 600298 -1.164349284   2.9485992
## 600299 -0.335891456   2.3230457
## 600300 -0.496458913   2.6140686
## 600301 -1.459114571   4.2730277
## 600302 -3.189289272   5.4006289
## 600303 -3.365800763   5.3707626
## 600305 -3.095944987   4.2362414
## 600306 -2.613336353   3.8846031
## 600307 -2.147222068   5.2895879
## 600308 -1.388840008   2.4401560
## 600309  0.601985012   0.2570944
## 600310 -1.947715257   6.5789084
## 600311  0.345424957   2.3696138
## 600312  0.752980897   1.6250233
## 600313 -3.700486219   8.9134649
## 600315  1.040316578   5.0991676
## 600316 -0.886092990   4.7946571
## 600317 -0.739022146   3.5947838
## 600318 -1.108221209   4.8971505
## 600319 -3.866830692   5.3080839
## 600320 -1.492794356   1.7134992
## 600321 -2.474941608   4.8759908
## 600322 -0.475790187   2.7020445
## 600323 -0.740438452   2.1432581
## 600325 -1.083811454   1.9061702
## 600326 -1.196888706   3.5736193
## 600327 -2.747877914   5.7902638
## 600328 -2.369952287   2.8777545
## 600329 -1.016430811   4.0612023
## 600330 -2.717230355   3.6206093
## 600331  1.859131536   0.4137030
## 600332 -0.319965695   2.4173016
## 600333 -3.394797370   4.8570019
## 600335 -1.700340209   3.3493164
## 600336 -1.260492211   3.4434372
## 600337 -0.820433562   3.0317769
## 600338 -0.006396586   4.4031162
## 600339 -1.004196494   1.8896215
## 600340 -9.201947084  10.1368053
## 600343 -1.301970626   7.4611293
## 600345 -2.843951390   6.9328780
## 600346 -2.028431676   4.2043631
## 600348 -3.285860843   5.3430569
## 600350  0.095494509   3.6612716
## 600351 -3.239096542   4.3624663
## 600352  1.211747355   2.0137349
## 600353 -4.510466239   7.1829074
## 600354 -1.023476329   5.8745153
## 600355 -2.749740614   5.7080983
## 600356 -2.034512093   3.7049266
## 600357 -3.597981998   6.0060424
## 600358 -3.590143699   4.3981263
## 600359 -4.692196226   6.4388669
## 600360 -1.671255613   2.2931384
## 600361  0.545106676   0.3528999
## 600362 -1.468518286   8.6989556
## 600363 -1.495443399   3.9319809
## 600365 -2.622895961   4.6218596
## 600366 -2.013969225   4.3472924
## 600367 -3.458800756   4.3742785
## 600368 -1.192491587   2.4434171
## 600369 -1.285841818   0.8808994
## 600370 -2.837910877   4.4729208
## 600371 -1.577048241   5.7215357
## 600372 -2.430904879   6.1043416
## 600373 -1.849050391   5.4183246
## 600375 -2.672122412   7.0622298
## 600376 -1.372017823   3.9432999
## 600377 -0.492146464   1.6180346
## 600378 -3.964377151   7.2832213
## 600379 -0.626872558   5.0861118
## 600380 -4.207220560   4.7037908
## 600381  1.239140148   2.1803912
## 600382 -2.753683578   3.2009993
## 600383  1.006462273   0.6841756
## 600385 -4.917016389   3.2880713
## 600386 -2.691943814   3.7587228
## 600387 -2.789227072   7.2546381
## 600388 -1.162975766   3.4113131
## 600389 -0.237591601   2.5358293
## 600390 -3.975684805   6.5203001
## 600391 -3.466446370   8.0156565
## 600392 -0.628955191   4.6612378
## 600393 -1.942499166   4.1318511
## 600395 -1.284512719   4.5294105
## 600396 -1.336367442   2.0146798
## 600397 -3.327341913   9.5411217
## 600398 -1.046463766   2.3795611
## 600399 -2.111732324   5.5541873
## 600400 -1.451692452   2.3466378
## 600401 -4.048982076   3.7641811
## 600403 -3.074807514   6.8612226
## 600405 -1.418201103   4.8795470
## 600406 -2.638582856   5.4598792
## 600408 -1.054615730   3.8039605
## 600409 -2.151377074   3.3773707
## 600410 -3.329905029   1.5069598
## 600415 -1.524810971   1.5890976
## 600416 -0.301222276   6.0001218
## 600418  0.901301840   1.6019195
## 600419 -1.261474995   4.4084965
## 600420 -2.613244035   4.8280254
## 600421 -6.775973952  12.3214389
## 600422 -3.083379017   3.0852776
## 600423 -3.381348881   5.5232159
## 600425 -1.190518749   5.1925109
## 600426 -1.683305838   3.6008720
## 600428 -0.884057840   2.3923097
## 600429 -1.280028928   4.8515175
## 600432  0.390810766   3.4258889
## 600433 -2.316510769   5.8298920
## 600435  0.634481217   2.0643690
## 600436 -0.217485424   5.8580312
## 600438 -0.495822420   0.6899026
## 600439 -0.065509918   1.0138310
## 600444  1.091820411   3.5705356
## 600446 -0.931783902   2.4508886
## 600448 -3.311983232   5.7137252
## 600449 -0.869725997   4.7043625
## 600452 -1.405040103   8.2256305
## 600455 -3.566963716   9.1271258
## 600456  2.013845622   2.3077771
## 600458 -2.986383009   5.8265457
## 600459  0.380621485   6.0612671
## 600460 -1.403636913   2.4836855
## 600461 -4.582603310   8.6772481
## 600462 -4.535361060   5.6447970
## 600463 -0.948028370   3.6858961
## 600466  0.515952659   3.4218224
## 600467  0.733005404   2.0439113
## 600468 -3.047770814   5.3343066
## 600469 -0.684649085   5.4028041
## 600470 -4.228304153   5.1923976
## 600475 -2.663420446   7.2330509
## 600476 -0.794167281   5.5626636
## 600477  1.589834827   4.9395822
## 600478  0.906799382   2.8369392
## 600479 -0.266557675   2.9800365
## 600480 -2.481186248   5.1417207
## 600481  0.352297819   4.8165017
## 600482  0.385784451   4.0676308
## 600483 -2.861113038   7.7402831
## 600485 -0.771736447   1.6346807
## 600486 -0.178594167   5.0417939
## 600487 -5.504330521   6.2253629
## 600488 -2.641633803   3.0582097
## 600489  2.359600544   4.0014864
## 600490 -4.469822364   8.2410893
## 600491 -0.547490747   4.0676543
## 600493 -4.038186551   8.6083632
## 600495 -0.447793444   3.2788782
## 600496  0.335086857   2.7257544
## 600497  1.944915107   2.0779558
## 600498 -3.222928434   7.8604292
## 600499 -1.234914264   3.3196150
## 600500 -1.282703770   2.4889254
## 600501 -2.565796787   2.7674402
## 600502 -1.738472018   5.2176170
## 600503 -2.140063872   7.7277662
## 600505 -3.151497618   7.5870131
## 600506  0.888008084   2.2392969
## 600507 -3.331416910   7.6442359
## 600508 -2.735667111   5.2760263
## 600509 -1.534090811   3.6218887
## 600510 -4.811131226   4.6942982
## 600511  6.243716182   2.2674111
## 600512 -3.286276719   3.7623051
## 600513 -1.964668583   3.7902648
## 600515 -2.741147945   5.6825964
## 600516 -3.526505959   3.8771040
## 600517  5.229305396   3.1851883
## 600518 -0.335727045   1.4273240
## 600519  4.621807535  -0.7854860
## 600520 -1.889136159   5.1665728
## 600521 -2.382892867   3.1429725
## 600522 -0.858947066   6.0026435
## 600523  1.356420918   4.4642423
## 600525 -2.695923126   4.9613926
## 600526 -0.851963654   4.3918273
## 600527 -1.273051780   4.1166177
## 600528  0.692086499   1.8574380
## 600529 -2.115910427   3.0567976
## 600530 -2.569149058   3.7118156
## 600531 -2.537034057   7.4670217
## 600532 -3.544432072   5.6353804
## 600533 -1.428969594   2.2690123
## 600535  1.193017005   2.5088555
## 600536 -1.789579429   4.3881278
## 600537 -5.171464975   8.5723148
## 600538 -2.969344503   4.4032078
## 600539 -3.959542794   5.5221046
## 600540 -2.723763534   6.3211287
## 600543  1.016248274   2.9589469
## 600545 -0.420942970   4.1451199
## 600546 -2.511672791   5.8943670
## 600547 -0.713524273   2.5014403
## 600548 -0.116995517   3.5973787
## 600549 -0.263518672   1.9291309
## 600550  1.865794925   1.1868677
## 600551 -1.671063561   4.8647429
## 600552 -3.105950358  11.8074760
## 600553 -2.185870554   5.7126727
## 600555  0.863631578   3.2017878
## 600556  0.725907000   1.5627579
## 600557  0.409854320   2.0555809
## 600558 -1.468760296   3.8359123
## 600559 -2.053824762   6.9238577
## 600560 -4.717006953   8.9365756
## 600561 -2.033790523   4.5860055
## 600562 -0.455846847   6.1363413
## 600563 -3.852579021   7.3633712
## 600565 -0.191444828   1.9506845
## 600566 -3.741562940   5.0042594
## 600567 -2.232178766   3.2458029
## 600568 -1.896180418   5.2261977
## 600569 -3.067584363   6.0717823
## 600570 -0.482878320   5.8498783
## 600571 -3.255629198   4.3787998
## 600572 -0.015147295   2.7869510
## 600573 -2.527246340   3.7052230
## 600575 -2.381121748   6.0095545
## 600576 -3.083253101   6.4381311
## 600577 -0.327582569   2.1324003
## 600578 -2.599169950   6.5874579
## 600579  0.779761248   7.9818203
## 600580 -2.645740307   4.3633945
## 600581 -3.248482429   8.2499527
## 600582  0.546102547   3.4874372
## 600583  2.250095830  -1.5937592
## 600584 -1.356490773   3.2809219
## 600585  1.067942597   0.2522520
## 600586  1.875855908   2.1962434
## 600587  0.122439110   3.5903102
## 600588 -0.262806734   2.1843726
## 600589 -1.824312424   2.5226676
## 600590 -1.831703783   4.7406766
## 600591 -2.323836472   7.3095204
## 600592 -1.869833429   3.4982945
## 600593 -3.863787698   6.7613148
## 600594  0.542162975   2.4634664
## 600595 -1.628155875   5.7363121
## 600596 -3.034470964   3.1386880
## 600597 -1.600015613   4.9679908
## 600598  0.304666689   2.4399221
## 600599  0.487667701   1.5395912
## 600600 -0.894548687   4.6917486
## 600601 -0.534913835   3.2492059
## 600602 -1.798084368   5.7472984
## 600603 -2.469258196   9.1426731
## 600604 -1.927447408   6.2466211
## 600605 -1.566875049   4.1689085
## 600606 -0.052338183   2.7800709
## 600607 -0.525226367   3.7307665
## 600608 -2.345574733   3.9859770
## 600609 -1.164339831   7.3348251
## 600610 -0.267942127   7.5022674
## 600611 -1.023837241   2.5223222
## 600612  0.849757758   3.3208631
## 600613 -0.652066408   2.5389138
## 600614 -0.367007312   1.8364116
## 600615 -2.361271117   4.6623456
## 600616 -1.614667353   2.5971544
## 600617 -0.396490404   2.7529341
## 600618 -0.204264877   2.7452647
## 600619 -0.855279856   2.6409089
## 600620 -0.881805435   2.9768905
## 600621 -1.936279019   4.0973378
## 600622 -2.802522748   4.3524839
## 600623 -1.067268453   4.8104038
## 600624 -3.064425499   4.3428732
## 600626 -1.717344319   3.8560251
## 600628 -1.768279463   3.2024538
## 600629 -2.821293005   7.9427509
## 600630 -2.106867196   3.6902548
## 600631 -0.431531260   3.1905036
## 600633 -1.660235460   2.6589287
## 600634 -2.814957955   5.2467305
## 600635 -1.269498195   3.7094043
## 600636 -2.924996609   2.6675710
## 600637 -3.399759538   6.1753153
## 600638 -0.668391184   2.5488613
## 600639 -1.673551404   4.2118689
## 600640 -1.520508087   3.6001942
## 600641 -1.688161271   5.5008469
## 600642 -1.740221183   3.6217723
## 600643 -2.738290250   5.7026287
## 600644 -3.478127808   4.5107194
## 600645 -3.078720925   3.9356092
## 600647 -0.465483008   1.9048448
## 600648 -1.171451665   4.2438576
## 600649 -2.177528724   4.1537102
## 600650 -2.398173150   2.6848146
## 600651 -1.894430036   4.1132314

由上，我們發現不管是固定效果還是隨機效果，STD前的係數都是負號。這樣跟高風險高報酬的認知不太一樣。雖然文獻上有兩支看法：抵換效果(trade-off)和槓桿效果(leverage)。但是，在整體上，正號依然是比較合理的綜合結果。這個問題，第12章會繼續討論。

4.3 不平衡追蹤資料簡介

不平衡追蹤資料(Unbalance panel data)是說假設我們有100家上市公司的財報資料，理想上的狀況當然是這100家公司的時間長度都一樣。但是，事實上，有的上市早，有的上市晚，所以，每一家的時間會不同；這種情況，我們稱之為不平衡，或不完整的追蹤資料。遇到這種狀況，一個作法就是取資料的交集，將之變成平衡的(Balance)。這樣的做法雖然沒錯，但是，第一、不忠於資料；第二、在時間短到寸土寸金的追蹤資料，取交集意味著刪除不完整資料，這樣恐怕損失很大。
理論上的估計，對於這種資料沒有什麼不一樣的問題。好比between estimator是將所有的資料平均後，變成橫斷面迴歸，這樣的話，平不平衡對於係數估計沒有太大關係，但是，估計變異數就有差異了。基本上，就是估計時，必須小心權重的建立，也就是自由度。
這種問題，所有的電腦程式都會主動處理和辨認，最重要的地方，也就是實證研究者很容易忽略的地方，是：如果手上的panel data是unbalance ，則時間的欄位必須要給。不然，一般軟體會任意用 $1,2,…,T$ 建立時間欄，這樣，會混淆了任一時間點 $N$ 的個數。也因為這個問題雖然很容易遇到，但是並不困難。

第 1。係數估計方面。以固定效果為例，在 $Q Transform$ 時，所有移除平均數的內容，都是依照資料去建立LSDV資料矩陣，摘除平均值後，就是OLS而已。其餘也類似。

第 2。變異數估計方面。估計變異數所需要的 $\Omega$ 矩陣，以 $N$ 只有兩家公司，一家時間長度為 $n1$ ，另一家時間長度是 $n2$ ，兩者交集是 $n2$，$n1$比$n2$ 再多個幾年。 $\Omega$ 展開如下：
\[ \Omega =\left[ \begin{matrix} \sigma _{\varepsilon }^{2}{{\mathbf{I}}_{n1}}+\sigma _{\mu }^{2}{{\mathbf{\tau }}_{n1n1}} & 0 & 0 \\ 0 & \sigma _{\varepsilon }^{2}{{\mathbf{I}}_{n1}}+\sigma _{\mu }^{2}{{\mathbf{\tau }}_{n1n1}} & \sigma _{\mu }^{2}{{\mathbf{\tau }}_{n1n2}} \\ 0 & \sigma _{\mu }^{2}{{\mathbf{\tau }}_{n2n1}} & \sigma _{\varepsilon }^{2}{{\mathbf{I}}_{n2}}+\sigma _{\mu }^{2}{{\mathbf{\tau }}_{n2n2}} \\ \end{matrix} \right] \]
除了下標 $n1n2$ 代表 $n1 \times n2$ 矩陣之外，其餘符號都同第三章。因此，只要這樣的矩陣建立好，單位向量的個數，會自動處理 $i$ 所需的權重，其餘就沒有太嚴重的問題。從電腦軟體的角度，必須賦予時間，他才能夠正確的展開這個矩陣，不然就會亂了。尤其是缺的值，不一定在頭尾，可能是在中間。所以，處理資料時，不可不慎。
Panel Data單根問題，就不會這樣，因為所採取的是完全異質的估計方法，也就是所有的 $N$ ，估計自己參數之後，再由 $N$ 的方向計算平均。
對plm而言，不平衡追蹤資料和平衡都是一樣的處理，畢竟載入資料後，宣告成追蹤資料時，只需宣告 $N$ 的欄位即可。

References

Greene, William H. 2012. Econometric Analysis. 7th ed. Boston: Prentice Hall.

Hsiao, Cheng. 2003. Analysis of Panel Data. 2nd ed. Econometric Society Monographs. Cambridge ; New York: Cambridge University Press.

最新版2022 ↩︎
pp.142-143↩︎

第 4 章 其他主題

4.1 維度 T 的異質性-雙維模型

4.2 變動係數 (variable coefficients models)

4.3 不平衡追蹤資料簡介

References

第 4 章其他主題