第 2 章 追蹤資料介紹
2.1 追蹤資料概說
前面我們介紹過的單維資料是純橫斷面(N),追蹤資料則是擴充了時間序列,因此具有兩維N,T的資料性質。好比1000家上市公司10年的財報數據,這樣的Panel 資料,N=1000,T=10。Panel Data的格式,是一家接著一家疊起來,如圖2.1 所示之Excel資料表。
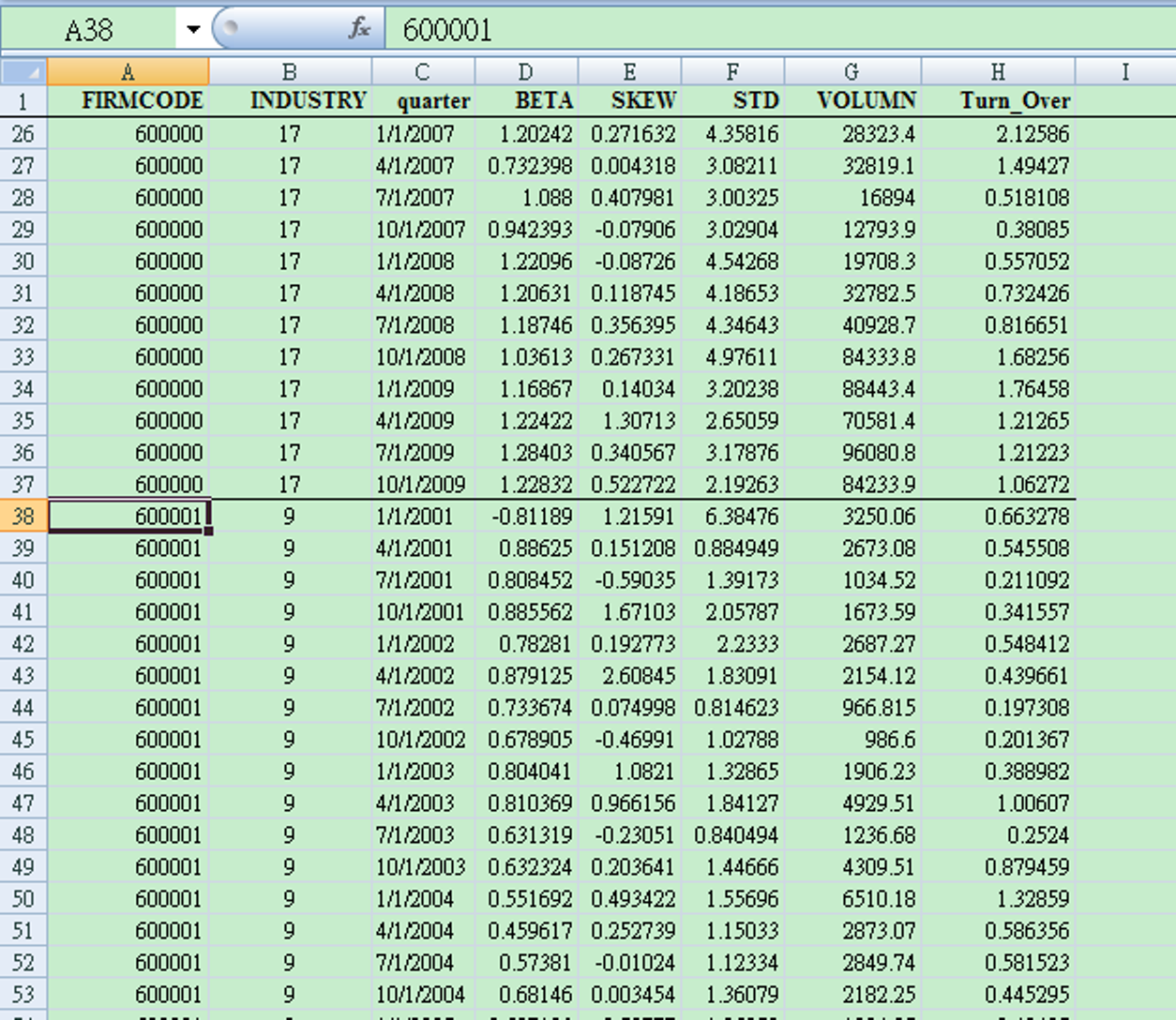
圖 2.1: Panel Data Structure
Panel data和一般的多變量模型(如VAR, SUR等等)的差異在於: 標準的追蹤資料是\(N\) 很大,\(T\) 相對較少。一般的多變量模型則是相反,\(T\) 需要較大。
除了\((N,T)\) 的相對大小之外,Panel data的資料有相當經濟意義。一筆Panel data,在資料增加上,從相對固定的時間長度來看,\(N\) 就有較多的增長。例如,上市公司和人口隨著時間增長,一個時間刻度,例如1年,\(N\)的數目是很多的。然而,以全球國家數量\(N\) 為的基礎之panel,就是一個意義上比較弱的panel,因為國家數目\(N\)幾乎是固定的,既使你認為國家也會增加,但是,在時間一年一年增加上,國家難得增加一個。
因為資料的意義,必須和模型的漸進性質相符合,Panel data估計式的漸進性質(\(i.e.\) 收斂至何種分配),是由\({N \to {\infty}}\) 的極限所得出,如下式.
\[ \underset{N\to \infty }{\mathop{\lim }}\,b=\beta \]
上面的極限,\(b\) 是樣本資料估計的參數,\(\beta\) 是母體值。雖然資料有時間,但是,\(b\) 往母體值\(\beta\) 的收斂過程,是由條件\(N \to \infty\) 驅動的。所以,如果我們實證資料的生成結構(generating structure)和\(N \to \infty\) 的狀況不太符合,雖然還是可以用 Panel 去分析,但是,必須知道解說的限制。 不然,變成一個軟體導向的議題分析就不妥了。
另一種稱為總體panel的資料型態,好比通貨膨脹率模型,時間T是月資料,商品別為N,這樣的總體panel data的漸進性質,稱為sequential limit,此處本書借用極限符號說明直覺。不強調區分哪一種收斂,也不用\(\delta-\epsilon\) 的極限方法作數學定義。如下:
\[
\underset{\begin{smallmatrix}
N\to \infty \\
T\to \infty
\end{smallmatrix}}{\mathop{\lim }}\,b=\beta
\]
也就是說,收斂過程在依序發生。這樣的情況,商品數\(N\) 會增長,時間\(T\) 也會增長。即使是季資料,也都是一個概念上還不錯的 Panel Data。Panel data 為何有用?
當被解釋變數的成分中, 有一部份受某種觀察不到的(unobserved)因子所影響,例如,菸酒的需求量和宗教因素的關係。宗教因子就是觀察不到但對菸酒需求有影響。且這些因子的忽略,會導致遺漏變數偏誤(omitted variable bias),但是,他們卻因為觀察不到,而無法蒐集資料納入迴歸。 這些因子在橫斷面\(N\) 不同,但是,不隨時間而變動;所以,Panel Data 可以控制觀察不到的因子對被解釋變數的影響。
假設純橫斷面資料迴歸(咖啡消費和所得),其中為咖啡消費與為所得影響,但另外也有一個觀察不到的變數,好比美國摩門教所在的州如Utah與其鄰近的州,咖啡因是被宗教禁止的。
如下面兩條方程式的迴歸:
\[ \tag{2.1A} y_{i}=a+b_1{x_i}+b_2{z_i}+{e_i} \]
\[
\tag{2.1B}
y_{t}=a+b_1{x_t}+b_2{z_t}+{e_t}
\]
Eq.(2.1A)是典型橫斷面迴歸,Eq. (2.1B)則是時間序列。這兩種型態的線性模式, 最小平方法的參數估計式是不偏且一致(Unbiased and Consistent Estimator)。但是,如果\(z\) 是觀察不到的變數,則資料上就無法收集資料,實證上就缺了這一個變數。若沒有\(z\),只能估計\(b_1\),但是因為遺漏變數問題,最小平方法估計的\(b_1\) 會不再是不偏的,這也就是遺漏變數偏誤(Omitted Variable Bias)問題。在缺少\(z\) 的強況下,只有當我們找到工具變數(Instruments),此工具變數和遺漏變數和殘差無關,但是和解釋變數相關,(2.1A)和(2.1B)使用工具變數估計法才會是不偏且一致的。但是,觀察不到的變數的兩種情況,panel data的架構均可以解決這個問題。
第1種情況。如果我們面對(2.1A),將之延伸為panel data。假設\(z_{it}\)不隨時間\(t\)變動,故\(z_{it}=z_i\):
\[ \tag{2.2A} \begin{align} {{y}_{it}} &= {{a}_{i}}+{{b}_{1}}{{x}_{it}}+{{b}_{2}}{{z}_{it}}+{{e}_{it}} \\ &= {{a}_{i}}+{{b}_{1}}{{x}_{it}}+{{b}_{2}}{{z}_{i}}+{{e}_{it}} \\ \end{align} \]
同步落後一期:
\[ \tag{2.2B} y_{it-1}=a_{i}+{b_1}{x_{it-1}}+{b_2}{z_i}+{e_{it-1}} \]
(2.2A)和(2.2B )兩式相減:
\[ \tag{2.2C} y_{it}-y_{it-1}=b_1 (x_{it}-x_{it-1})+(e_{it}-e_{it-1}) \]
差分迴歸也稱為是輔助迴歸方程式(auxiliary regression equation)。因此,透過估計
\(\Delta y_{it}=b_1 \Delta x_{it} + \Delta e_{it}\) 可以將原先我們想知道的係數 \(b_1\) 估計出來。
第2種情況。如果我們面對(2.1B),將之延伸為panel data。假設\(z_{it}\) 不隨\(i\) 變動,故\(z_{it}=z_t\)。 故可以使用均數移除法(de-mean):移除每一個時間點的橫斷面平均(cross-section average over time),如下式:
\[
\tag{2.3A}
\begin{align}
{y_{it}} &= a_i + {b_{1}}x_{it} + {b_{2}}z_{it} + e_{it} \\
&= a_i + b_{1}x_{it} + b_{2}z_{t} + e_{it}
\end{align}
\]
根據 Eq.(2.1A)
\[
\tag{2.3B}
\bar y_t= a+b_1 \bar x_t + b_2 {z_t} + \bar {e_t}
\]
(2.3B)是不偏且一致。(2.3A)減( 2.3B)得到下式:
\[
\tag{2.3C}
{y_{it}- {\bar y_{t}}}=b_1 ({x_{it}- \bar x_{t}})+({e_{it}- \bar e_{t}})
\]
理論上,Eqs.( 2.2C)和(2.3C)的估計出來的\(b_1\) 均是Eq.( 2.1)的不偏且一致估計式 。但是,如果資料是除時間序列(N=1)或純橫斷面(T=1),Eqs. (2.2C)和(2.3C)的轉換就不可行,只有Panel Data可以這樣轉換。這個例子在理論上說明了Panel Data的用處。我們必須注意(2.2C)的結果, 隱含了殘差項是係數為\(-1\) 的移動平均過程 (Moving Average Process),這個問題,我們在動態和序列相關時,再繼續討論。
這裡必須注意,係數 \(b_1\) 的意義,必須是在 \(y=a+b_1x+b_2z\) 的架構下去解釋參數。也就是說,解釋\(b_1\) 時必需先說「其他條件不變」,其餘同線性模式。文獻上的經典案例不少:
其一是 MaCurdy (1981) 的勞動供給研究,不論在在橫斷面迴歸時,一項重要但是觀察不到的變數就是勞動者期初財富的邊際效用(marginal utility of initial wealth),這項變數可以是為勞動者的終身薪資(lifetime wages)和非薪資所得(property income)。因此,任何可用的經濟工具變數,如教育,均和此觀察不到的經濟變數高度相關。這樣的情況,工具變數法就變的不可行。假設觀察不到的邊際效用變數不會隨時間變動,故 MaCurdy (1981) 利用了panel data和Eq.(2.2C)的一階差分迴歸, 移除了邊際效用變數。
其二是經濟成長的研究,如 Barro and Sala-i-Martin (2004) 所介紹。經濟成長決定式中,有一項變數很重要, 就是國家的技術效率,但是,技術效率卻無法量化。另外,根據經濟學原理,技術效率和投資成正相關,因此,這個觀察不到的變數和解釋變數之間,高度相關。遺漏了一個高度相關的變數,使的橫斷面迴歸估計式,有著嚴重的遺漏變數偏誤問題。 Steven N. Durlauf (2001) 和 Steven N. Durlauf, Johnson, and Temple (2005) 介紹了panel data於此的用處。
綜合說之,Panel data的好處如下:
(1) 可以控制個別異質性。例如, Baltagi and Levin (1992) 研究了1963-1988 美國46個州的香菸需求。
香菸的消費設為價格和所得及消費落後其的動態函數。這些變數隨時間(\(\lambda_t\))及橫段面差異(如區域\(Z_i\) )變動。\(\lambda_t\) 的例子如一些隨時間及區域變動的變數是無法觀察的。好比全國性廣告,\(Z_i\)的例子如各州宗教與教育。
(2) 另外,從純粹橫斷面資料,增加時間序列,允許研究者檢視許多重要的理論意義問題。例如, Ben-Porath (1973) 從橫斷面資料中,發現在一定的時間內,已婚婦女平均年勞動參與率為50%。純粹橫斷面資料中,勞動力流動程度的解釋有二:一個極端解釋可成:在同質人口樣本中,每一個婦女在某一年,均有50%的機會參與勞動,所以勞動力流動程度高。 另一個極端可解釋成:在異質人口樣本中,50%的婦女總是參與勞動,50%的婦女從不參與勞動,故勞動力流動程度低。
(3) 增加時間序列可以避免這兩種極端的衝突。Panel Data因為增加了時間序列維,樣本增加,提升估計效率。更多資料樣本,自由度增加,線性重合程度下降(因N維度增加而增加變異)。且建立在個體單位,故加總偏誤較小。
(4) 最後,Panel data允許我們檢定較精細的行為假說。例如,生產效率以追蹤資料較好。大致上來說,兼顧時間序列和橫斷面資料的優點。
Panel Data缺點則是:
(1) 資料收集不易。因為T往往很小。
(2) 衡量誤差嚴重。追蹤個體時,記錄資料的問題。
(3) 選擇性(selectivity)問題
(3.1) Self-selectivity:人們因心中欲求工資高於市場工資,故選擇不工作。因此,我們只觀察到人的特徵,不是工資。但是,當工資沒有時,這個樣本就被除去(censored),造成統計偏誤。
(3.2) Non-response: 拒絕參與或受訪。
(3.3) Attrition: 受追蹤單位突然失蹤。研究期滿,往往遺失很多樣本。
2.2 基本線性模式
令\(u_{it}\) 為誤差項,Panel data 的迴歸方程式可以表示如下:
\[
\begin{aligned}
{{y}_{it}}&=a+{{b}_{1}}{{x}_{1,it}}+{{b}_{2}}{{x}_{2,it}}+\cdots +{{u}_{it}}
=a+\sum\limits_{\kappa =1}^{K}{{{b}_{\kappa }}{{x}_{\kappa ,it}}}+{{u}_{it}} \\
i&=1, 2,...N ; \;\;t=1, 2,...T
\end{aligned}
\]
這樣的結構,有幾種處理資料的方法,應用的是\(LS\)估計式
(1) Pooled OLS, population-averaged
\[ {{y}_{it}}=a +{b_{1}}{{x}_{1,it}}+b_{2}{{x}_{2,it}}+{{u}_{it}} \]
Pooled OLS就是一般的OLS迴歸,在所有的\(N/T\)資料中,只有一個共同截距\(a\)。
(2) Between Estimator
\[
{{\bar{y}}_{i}}=a +b_{1}{{\bar{x}}_{1,i}}+b_{2}{{\bar{x}}_{2,i}}+({{\mu }_{i}}+{{\bar{\varepsilon }}_{i}})
\]
Between Estimator其實就是取時間平均,將資料轉成純橫斷面資料。
(3) Within Estimator
\[
{{y}_{it}}-{{\bar{y}}_{i}}=a + b_{1}({{x}_{1,it}}-{{\bar{x}}_{1,i}}) + b_{2}({{x}_{2,it}}-{{\bar{x}}_{2,i}}) + ({{u}_{it}}-{{\bar{u}}_{i}})
\]
Within Estimator就是我們從殘差項分離出來的橫斷面效果模型,也就是固定效果。 Dhrymes (2013) 2 指出Within group的說法是名稱的誤置(misnomer),Within/Between group 的概念行之於ANOVA,但是,和固定效果的處理方式與分析無關。
我們也稱此為殘差成分迴歸(Error Component Regression),結構如圖 2.2所示。主要的參數是橫斷面效果 \(\mu_i\) 和縱斷面期間\(\lambda_t\) ,常用的估計方法在最底下一列。
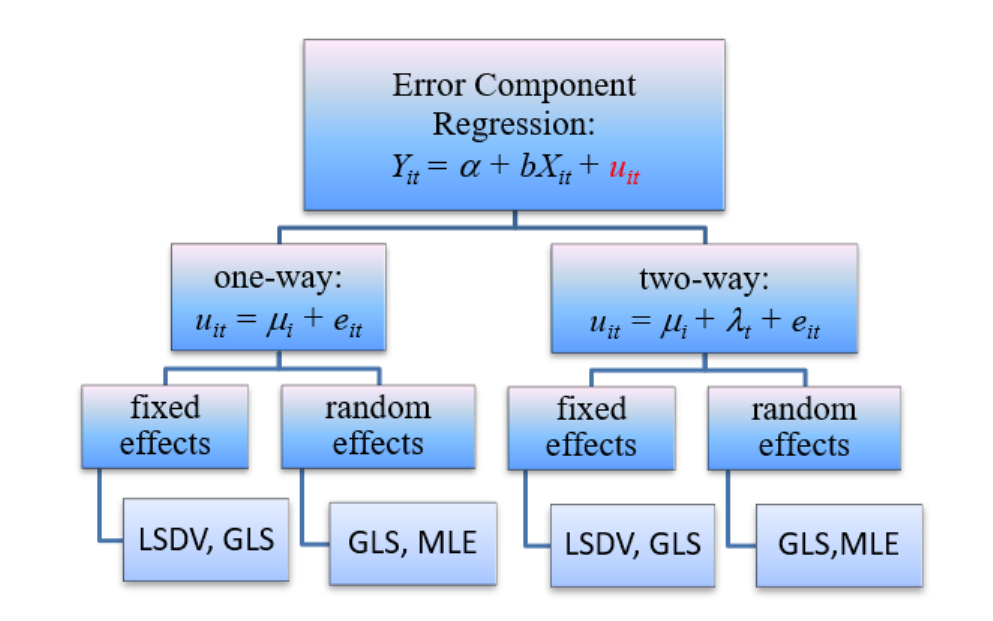
圖 2.2: Error Component 模型結構
\(\mu_i\) 就是個別效果。固定效果和隨機效果的假設,一般多有誤解為:固定效果就是 \(\mu_i\) 是固定且非隨機的。然後,隨機效果則是 \(\mu_i\) 是隨機變數。
其實不是這樣,固定效果在於將「個別效果 \(\mu_i\)」與「解釋變數」間的關係,視為是一個固定的隨機變數。所以是說「相關性」是固定;既然是固定的,代表「有」相關。同理,隨機效果描述了個別效果項目和解釋變數之間的關係是隨機的,隨機意味著期望值為0,也就是「無關」。所以, Lee (2002) 用related effect 代替固定效果一詞,用unrelated effect代替隨機效果。 Greene (2012) 的第11章也有明確的說明。
我們將橫斷面效果分成固定效果(fixed)和隨機效果(random),期間效果也是如此。至於是哪一種效果才是正確的設定,必須透過Hausman test的檢定才能知道, 後面對此會詳細說明。 Panel data估計式的分配之收斂,是來自於\(N \to \infty\)。
最後,如圖2.2,一條panel data的迴歸方程式,對 \(N\) 而言, 斜率參數\(b\)是共同的, \(N\) 的差異表現在截距上。也就說它的實證意義是一個 「共同斜率,異值截距」的概念。如果要考慮「截距不同,斜率也不同」,就是完全異質的總體追蹤資料(macro panel)的性質;例如,30個國家的月通貨膨脹率,100個產業的產出指數等等。這樣完全異值panel,不是標準的個體panel。因為它須要較長的時間序列來估計個別斜率,在資料型態較接近高維度的多變量資料。在非定態時間序列內,倒是常見的型態。
2.3 R資料建立
我們先學習如何將資料載入R。我們分兩種情況介紹。就時間長短而言,有兩種資料。
(1)Balanced panel: 對所有的N,時間樣本數T皆相同。
(2)Unbalanced panel:對所有的N,時間樣本數T不一樣。好比上市公司,有的上市早,有的上市晚。
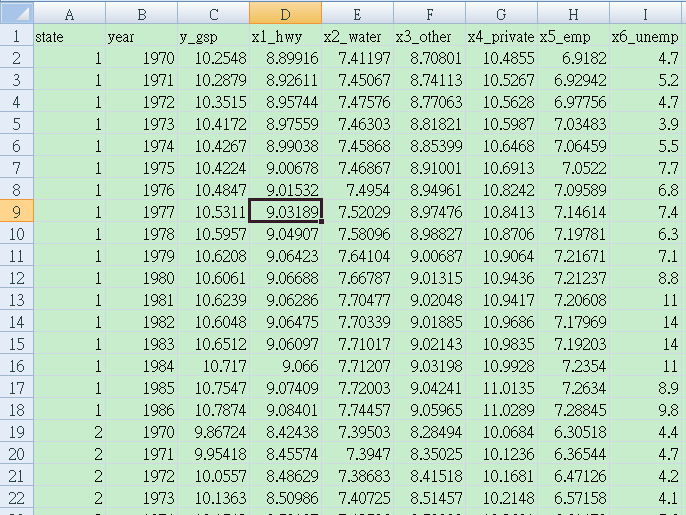
圖 2.3: 以美國州為N的Panel Data
state=1, 2,…,48 states(N)
year=1970,1971,…,1986(T)
y_gsp= log(gross state product)
x1_hwy= log(high-way component of public capital)
x2_water= log(water component of public capital)
x3_other=log(other component of public capital)
x4_private=log(private capital stock)
x5_emp=log(non-agricultural payrolls)
x6_unemp= unemployment rate of state
這筆原始資料為productivity.csv,讀進R之後,必須宣告這筆資料是Panel data。要宣告這筆資料是panel data,只需要宣告時間 \(T\) 或橫斷面 \(N\) 的欄位代號即可。 這筆資料,時間代號是 \(year\),橫斷面代號是 \(state\)。
Step 1. 載入資料
## state year y_gsp x1_hwy x2_water x3_other x4_private x5_emp x6_unemp
## 1 1 1970 10.2548 8.89916 7.41197 8.70801 10.4855 6.91820 4.7
## 2 1 1971 10.2879 8.92611 7.45067 8.74113 10.5267 6.92942 5.2
## 3 1 1972 10.3515 8.95744 7.47576 8.77063 10.5628 6.97756 4.7
## 4 1 1973 10.4172 8.97559 7.46303 8.81821 10.5987 7.03483 3.9
## 5 1 1974 10.4267 8.99038 7.45868 8.85399 10.6468 7.06459 5.5
## 6 1 1975 10.4224 9.00678 7.46867 8.91001 10.6913 7.05220 7.7 Step 2.建立panel data。
宣告這筆資料的panel維度 N和 T:index=c(“state”,“year”)
Step 3.看看資料
## state year y_gsp x1_hwy x2_water x3_other x4_private x5_emp x6_unemp
## 1-1970 1 1970 10.2548 8.89916 7.41197 8.70801 10.4855 6.91820 4.7
## 1-1971 1 1971 10.2879 8.92611 7.45067 8.74113 10.5267 6.92942 5.2
## 1-1972 1 1972 10.3515 8.95744 7.47576 8.77063 10.5628 6.97756 4.7
## 1-1973 1 1973 10.4172 8.97559 7.46303 8.81821 10.5987 7.03483 3.9
## 1-1974 1 1974 10.4267 8.99038 7.45868 8.85399 10.6468 7.06459 5.5
## 1-1975 1 1975 10.4224 9.00678 7.46867 8.91001 10.6913 7.05220 7.7## Balanced Panel: n = 48, T = 17, N = 816上面這筆資料是balanced panel,所以Step 2. 也可以直接在後面輸入N的數量, 例如:
## state year y_gsp x1_hwy x2_water x3_other x4_private x5_emp x6_unemp id
## 1-1 1 1970 10.2548 8.89916 7.41197 8.70801 10.4855 6.91820 4.7 1
## 1-2 1 1971 10.2879 8.92611 7.45067 8.74113 10.5267 6.92942 5.2 1
## 1-3 1 1972 10.3515 8.95744 7.47576 8.77063 10.5628 6.97756 4.7 1
## 1-4 1 1973 10.4172 8.97559 7.46303 8.81821 10.5987 7.03483 3.9 1
## 1-5 1 1974 10.4267 8.99038 7.45868 8.85399 10.6468 7.06459 5.5 1
## 1-6 1 1975 10.4224 9.00678 7.46867 8.91001 10.6913 7.05220 7.7 1
## time
## 1-1 1
## 1-2 2
## 1-3 3
## 1-4 4
## 1-5 5
## 1-6 6另外,index=內的 “year” 也可以省略,只需要 “state” 就可以。確認維度
## state year y_gsp x1_hwy x2_water x3_other x4_private x5_emp x6_unemp
## 1-1 1 1970 10.2548 8.89916 7.41197 8.70801 10.4855 6.91820 4.7
## 1-2 1 1971 10.2879 8.92611 7.45067 8.74113 10.5267 6.92942 5.2
## 1-3 1 1972 10.3515 8.95744 7.47576 8.77063 10.5628 6.97756 4.7
## 1-4 1 1973 10.4172 8.97559 7.46303 8.81821 10.5987 7.03483 3.9
## 1-5 1 1974 10.4267 8.99038 7.45868 8.85399 10.6468 7.06459 5.5
## 1-6 1 1975 10.4224 9.00678 7.46867 8.91001 10.6913 7.05220 7.7
## time
## 1-1 1
## 1-2 2
## 1-3 3
## 1-4 4
## 1-5 5
## 1-6 6## Balanced Panel: n = 48, T = 17, N = 816如果載入的是unbalanced panel,則只須在index宣告橫斷面(N)的欄為名稱即可,如下例 index="townid"。
## mv crim zn indus chas nox rm age dis rad
## 1 10.08580 0.00632 18 2.309999 no 28.9444 43.2306 65.19995 1.40854 0.00000
## 2 9.98045 0.02731 0 7.070000 no 21.9961 41.2292 78.89996 1.60283 0.69315
## 3 10.45450 0.02730 0 7.070000 no 21.9961 51.6242 61.09998 1.60283 0.69315
## 4 10.41630 0.03237 0 2.179998 no 20.9764 48.9720 45.79999 1.80207 1.09861
## 5 10.49680 0.06905 0 2.179998 no 20.9764 51.0796 54.19998 1.80207 1.09861
## 6 10.26470 0.02985 0 2.179998 no 20.9764 41.3449 58.69998 1.80207 1.09861
## tax ptratio blacks lstat townid
## 1 296 15.29999 0.39690 -3.00074 1
## 2 242 17.79999 0.39690 -2.39251 2
## 3 242 17.79999 0.39283 -3.21165 2
## 4 222 18.70000 0.39464 -3.52744 3
## 5 222 18.70000 0.39690 -2.93163 3
## 6 222 18.70000 0.39412 -2.95555 3## Unbalanced Panel: n = 92, T = 1-30, N = 506接下來,我們介紹R裡面如何處理panel data的敘述統計。因為panel data有\(N/T\)兩維, 所以,aggregate()是一個好用的函數。
上面語法內有3個條件:
第1個 Data 是要計算的資料。
第2個 by 是宣告要依照那個group變數計算。
第3個 FUN 是統計函數。內建的mean, sd, median, sum都可以用。
取第3~5欄的數據為例,以\(N\)的維度(州)當作群組因子,計算平均數;結果如下
## Group.1 y_gsp x1_hwy x2_water
## 1 1 10.537524 9.023266 7.584079
## 2 2 10.313366 8.606226 7.627664
## 3 3 9.978131 8.359488 6.693631
## 4 4 12.751482 10.724653 9.966921
## 5 5 10.559894 8.598005 7.990227
## 6 6 10.727682 8.887779 8.019991
## 7 7 9.027435 7.648294 5.947675
## 8 8 11.548818 9.656973 8.691426
## 9 9 11.012324 9.185508 8.023579
## 10 10 9.187805 7.862686 5.688315
## 11 11 12.009612 10.183006 9.023567
## 12 12 11.103853 9.224494 8.035675
## 13 13 10.490829 9.190785 7.527006
## 14 14 10.363194 8.815049 7.483055
## 15 15 10.606759 9.292272 7.639480
## 16 16 11.153276 9.359324 7.989711
## 17 17 9.325815 7.814329 6.627959
## 18 18 10.851894 9.153248 8.532005
## 19 19 11.231500 9.108265 8.138515
## 20 20 11.693059 9.870231 9.212723
## 21 21 10.870741 9.370443 8.376991
## 22 22 10.048449 8.694924 6.943479
## 23 23 11.004882 9.291499 8.033442
## 24 24 9.196042 8.262876 6.153978
## 25 25 9.893726 8.481211 7.140619
## 26 26 9.330965 7.715776 6.499502
## 27 27 9.210826 7.700307 6.131495
## 28 28 11.539276 9.481476 8.547279
## 29 29 9.763386 8.181675 6.834925
## 30 30 12.464941 10.492935 9.712475
## 31 31 11.075476 9.161034 8.042875
## 32 32 9.063553 7.990866 6.003860
## 33 33 11.835376 10.102376 9.096852
## 34 34 10.617582 8.702008 7.497586
## 35 35 10.316576 8.746781 7.738572
## 36 36 11.873806 10.114832 9.000304
## 37 37 9.275728 7.618365 6.486675
## 38 38 10.268259 8.412864 7.426316
## 39 39 8.909412 8.071612 5.773082
## 40 40 10.785912 9.227402 8.224674
## 41 41 12.302171 10.304753 9.298282
## 42 42 9.657625 8.208090 6.514127
## 43 43 8.592964 7.561374 5.629408
## 44 44 11.077282 9.500526 8.207567
## 45 45 10.859782 9.244193 8.361475
## 46 46 9.933732 8.770141 6.450251
## 47 47 10.947018 9.257550 8.403084
## 48 48 9.235048 7.988612 5.818362接下來,我們可以再看看更多的技巧
## Group.1 y_gsp x1_hwy x2_water x3_other x4_private x5_emp x6_unemp
## 1 1970 10.26265 8.772145 7.357491 8.483713 10.28133 6.754859 4.897917
## 2 1971 10.29069 8.802049 7.379766 8.539530 10.32190 6.768538 5.677083
## 3 1972 10.34933 8.831535 7.398235 8.582679 10.35458 6.817696 5.214583
## 4 1973 10.40995 8.854846 7.415793 8.621305 10.39279 6.869372 4.677083
## 5 1974 10.40687 8.877974 7.442667 8.650274 10.44002 6.895158 5.339583
## 6 1975 10.39544 8.892020 7.477948 8.689835 10.48164 6.886258 8.052083
## 7 1976 10.44356 8.901456 7.521402 8.725270 10.51973 6.926256 7.027083
## 8 1977 10.49077 8.912959 7.564736 8.751479 10.53985 6.970874 6.529167
## 9 1978 10.55060 8.920571 7.607156 8.768436 10.56942 7.027527 5.535417
## 10 1979 10.58209 8.926909 7.655359 8.792176 10.60694 7.063805 5.425000
## 11 1980 10.57705 8.931716 7.693330 8.814148 10.64755 7.067658 6.779167
## 12 1981 10.60056 8.936266 7.730411 8.834435 10.67132 7.074418 7.277083
## 13 1982 10.57929 8.938876 7.753043 8.845004 10.70024 7.054977 9.300000
## 14 1983 10.60466 8.941675 7.772367 8.848322 10.71546 7.062733 9.279167
## 15 1984 10.67009 8.947114 7.786658 8.850666 10.72793 7.108467 7.231250
## 16 1985 10.70413 8.954818 7.807696 8.855125 10.75570 7.134603 7.066667
## 17 1986 10.73271 8.964289 7.832662 8.865541 10.78444 7.151266 6.929167上面的語法是將欄位的前兩欄的維度資料去掉,其餘的全要,然後,依照時間T維度(year),計算平均數,這樣算出來的,其實就是橫斷面平均時間序列資料:每一年都是48州的平均。
如果需要更多的統計衡量函數,例如,偏態和峰態等等,可以載入第1章套件fBasics就可以。以下我們計算了前2個變數,各州的偏態。
## Group.1 y_gsp x1_hwy
## 1 1 -0.2105627325 -0.83279978
## 2 2 -0.0357220612 -0.04786080
## 3 3 -0.3083088252 -0.49821627
## 4 4 -0.0071189035 -0.08022524
## 5 5 -0.3277659917 -0.66210023
## 6 6 0.7325693423 -0.20033302
## 7 7 0.1369452344 0.42797071
## 8 8 0.0001129449 -0.48736557
## 9 9 0.1861558517 -0.17213508
## 10 10 -0.6707596970 -0.62314337
## 11 11 -0.1465364213 -0.89078291
## 12 12 -0.2546422979 -1.05499112
## 13 13 -0.6945365156 -0.93182541
## 14 14 -0.1179150545 -0.43365477
## 15 15 -0.4375334692 -0.40563268
## 16 16 -0.0599665016 -0.23832686
## 17 17 0.1821148485 -1.50331311
## 18 18 0.4051278860 -0.56401170
## 19 19 0.8918888274 -2.27823336
## 20 20 -0.0786218313 -0.86419011
## 21 21 0.0623605507 -0.63006847
## 22 22 -0.4485579344 -0.59302531
## 23 23 0.0616310554 -1.36264662
## 24 24 -0.5780291166 -1.35261489
## 25 25 -0.2087541471 -0.49339728
## 26 26 -0.2260677845 0.30240988
## 27 27 0.3716060498 -0.89189853
## 28 28 0.6359777516 -1.67074743
## 29 29 -0.2971444538 0.79311880
## 30 30 1.3007121910 -0.48850249
## 31 31 0.0536366217 -0.97981236
## 32 32 -0.7053296180 -0.51959064
## 33 33 -0.1196684096 -0.29588158
## 34 34 -0.1196258193 0.25828690
## 35 35 -0.6298727650 -1.12366328
## 36 36 0.0317357746 -0.90773851
## 37 37 0.9842893334 0.18189970
## 38 38 -0.0426944655 -0.91937185
## 39 39 -0.5491213084 -1.03663875
## 40 40 -0.2261117948 -0.63845588
## 41 41 -0.2858279991 -0.08278036
## 42 42 -0.2269871962 -0.51297307
## 43 43 0.4774330930 -0.10689616
## 44 44 0.0255346108 -0.76295989
## 45 45 -0.3292127196 -0.51051257
## 46 46 -0.4383217323 -1.10791852
## 47 47 -0.1800511121 -0.94778584
## 48 48 -0.1403617810 0.59317444arrgegate()函數的群組變數,在此例是用數字,但也可以是文字。讀者可以用第1章使用的140個國家經常帳資料,依照六個經濟發展程度計算統計量。這樣就可以看到R的資料處理,不但很好用,而且十分美觀。
References
Page 341↩︎