第 3 章 維度 N 的異質性：單維模型


圖2.2的Error Component最下方所列 處理橫斷面異質性的兩個方法： 固定效果和隨機效果；根據這兩種方法，已知一個迴歸方程式

\[ \tag{3.1A} y_{it}=a+b x_{it}+ u_{it} \]
若橫斷面個別效果有異質性，故 \(u_{it}=\mu_i + e_{it}\) ， \(\mu_i\) 就是橫斷面的個別效果； 所以，套入 (3.1A)後，如下：
\[ \tag{3.1B} y_{it}=a+b x_{it}+ \mu_i + e_{it} \]
接下來就是估計橫斷面效果 \(\mu_i\)，有兩種作法：

 (1) 假設其為固定效果(fixed-effects)，也就是說 \(\mu_i\) 和 \(x\) 有關且關係為固定。這樣的想法，就是把 \(\mu_i\) 想成用「固定資料」估計出來的係數，所以，這固定的資料和 \(x\) 的關係就是固定的。固定效果直接面對的方程式是(3.1B)，基本的架構就是估計截距用的虛擬變數法，把 \(\mu_i\) 從 \(y_{it}\) 取出來。

 (2) 假設其為隨機效果(random-effects)，也就是說 \(\mu_i\) 和 \(x\) 的關係是隨機的，像在路上撿到錢一樣，有時後有，有時後沒有。所以，這個隨機關係的期望值假設為0。隨機效果直接面對的方程式是(3.1A)的pooling regression 的複合殘差 \(u_{it}\) ，再從複合殘差的機率分配中，取出個別效果 \(\mu_i\) ， 因此只要做好動差分配的假設，GLS就可以從複合殘差之中取出個別效果。下面會繼續解釋。

另外，Eq.(3.1B)的 \(y_{it}=a+b x_{it}+ \mu_i + e_{it}\) 和第二章的 within estimator的de-mean 是一樣的， 用簡單的代數就可以證明，已知一個單變數迴歸
\[ y_i=a+b x_i+e_i \] 已知 \(\bar y_i=a+b \bar x_i\) ，將 \(a=\bar y_i-b \bar x_i\) 代入上式

\[ y_i- \bar y_i= b(x_i- \bar x_i)+e_i \]
所以，de-mean regression的 within-estimator，就可以處理 panel data 之下的固定個別效果。 下一節，我們將介紹常用的矩陣代數方法 \(Q \; transform\) ，將代數運算一般化。


3.1 固定效果


固定效果假設 \(\mu_i\) 和殘差 \(e_{it}\) 的相關是固定的，也就有相關。 固定效果的估計方法有二：LSDV 和GLS。固定效果的估計，原理上是利用稱為 \(Q \;transform\) 的矩陣運算技巧，將個別效果當成截距移除，之後再進行估計。我們先說明 \(Q \;transform\) 的原理。先從一個 \(k\) 個解釋變數的時間序列迴歸模型出發：
\[ {{y}_{t}}=a+{{b}_{1}}{{x}_{1t}}+{{b}_{2}}{{x}_{2t}}+\cdots +{{b}_{k}}{{x}_{kt}}+{{u}_{t}} \\ t=1,2,...,T \]
上式可寫成如下矩陣：
\[ \tag{3.2} y=a+Xb+u \]
定義一個矩陣 \(\mathbf{Q}={{\mathbf{I}}_{\mathbf{T}}}-\frac{\mathbf{\tau {\tau }'}}{\mathbf{T}}\)
\(\begin{aligned} {{\mathbf{I}}_{\mathbf{T}}}&=\left[ \begin{matrix} 1 & 0 & \cdots & \cdots & 0 \\ 0 & 1 & \cdots & \cdots & \vdots \\ \vdots & \vdots & \ddots & \cdots & \vdots \\ \vdots & \vdots & \vdots & \ddots & 0 \\ 0 & \cdots & \cdots & 0 & 1 \\ \end{matrix} \right] \end{aligned}\)
是一個 \(T \times T\) 主對角線為1的方陣

\(\begin{aligned} \mathbf{\tau }=\left[ \begin{matrix} 1 \\ \vdots \\ \vdots \\ 1 \\ \end{matrix} \right] \end{aligned}\) 是一個\(T \times 1\) 且元素全是1的列向量

令 \(\mathbf{P}=\frac{\mathbf{\tau {\tau }'}}{T}\) ，也可以寫成 \(\frac{\mathbf{\tau {\tau }'}}{T}=\mathbf{\tau }{{(\mathbf{\tau {\tau }'})}^{-1}}\mathbf{{\tau }'}\)


故 \(\mathbf{Q}\) 矩陣也可以寫成 \(\mathbf{Q}={{\mathbf{I}}_{\mathbf{T}}}-\mathbf{P}\)

 第1、任何向量前乘(pre-multiply) \(\frac{\mathbf{\tau {\tau }'}}{T}\) 的運算，就是計算其平均。解說如下：
\[ \frac{\mathbf{\tau {\tau }'}}{T}{{y}_{t}}=\frac{1}{T}\left[ \begin{matrix} 1 \\ \vdots \\ 1 \\ \end{matrix} \right]\left[ \begin{matrix} 1 & \cdots & 1 \\ \end{matrix} \right]\left[ \begin{matrix} {{y}_{1}} \\ \vdots \\ {{y}_{T}} \\ \end{matrix} \right]=\frac{1}{T}\left[ \begin{matrix} 1 \\ \vdots \\ 1 \\ \end{matrix} \right]\sum\limits_{i=1}^{T}{{{y}_{i}}}=\frac{1}{T}\left[ \begin{matrix} \sum\limits_{i=1}^{T}{{{y}_{i}}} \\ \vdots \\ \sum\limits_{i=1}^{T}{{{y}_{i}}} \\ \end{matrix} \right]=\left[ \begin{matrix} {\bar{y}} \\ \vdots \\ {\bar{y}} \\ \end{matrix} \right] \]
 第2、任何向量前乘方陣 \({\mathbf{I}}_{\mathbf{T}}\) 的運算，還是其自己
\[ {{\mathbf{I}}_{\mathbf{T}}}{{y}_{t}}=\left[ \begin{matrix} 1 & 0 & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & 1 \\ \end{matrix} \right]\left[ \begin{matrix} {{y}_{1}} \\ \vdots \\ {{y}_{T}} \\ \end{matrix} \right]=\left[ \begin{matrix} {{y}_{1}} \\ \vdots \\ {{y}_{T}} \\ \end{matrix} \right] \]
所以，\(\mathbf{Q}{{y}_{t}}=\left( {{\mathbf{I}}_{\mathbf{T}}}-\frac{\mathbf{\tau {\tau }'}}{\mathbf{T}} \right){{y}_{t}}\) 就是移除平均數(de-mean)。因此，Eq.(3.2) 經由\(\mathbf{Q}\)轉換後變成\(\mathbf{Q}{{y}_{t}}=\mathbf{Q}a +\mathbf{QX b }+\mathbf{Q}{{u}_{t}}\)
\[ \tag{3.4} \mathbf{Q}{{y}_{t}}=\mathbf{QX b }+\mathbf{Q}{{u}_{t}} \]
應用最小平方法去估計Eq.(3.3)，得到
\[ \tilde{b}_{LS}={{\left( \mathbf{{X}'{Q}'QX} \right)}^{-1}}\mathbf{{X}'{Q}'Q}{{y}_{t}} \]
因為 \(\mathbf{Q}\) 是symmetric idempotent矩陣，故 \(\mathbf{{Q}'Q}={{\mathbf{Q}}^{2}}=\mathbf{Q}\) ，所以最小平方法估計式可化簡為
\[ \tag{3.5} \tilde{b}_{LS}={{\left( \mathbf{{X}'QX} \right)}^{-1}}\mathbf{{X}'Q}{{y}_{t}} \]
且
\[ \tag{3.6} \operatorname{var}(\tilde{b}_{LS})=\sigma _{u}^{2}{{\left( \mathbf{{X}'QX} \right)}^{-1}} \]
因此，給定解釋變數 \(X\) ，根據Gauss-Markov 定理，Eq.(3.5)的估計式具有BLUE(Best Linear Unbiasedness Estimate)性質。在panel data， \(Q \;transform\) 的技巧， 只須要用Kronecker product展開成 \({{\mathbf{I}}_{\mathbf{N}}}\otimes \mathbf{Q}\) 就可以直接應用於 \(N \times T\) 維度的資料。Panel Data的矩陣推導， 讀者可以自行練習。我們接下來由較簡單的方式解說。

 估計方法 1. LSDV(Least square Dummy Variable)
這個方法將以虛擬變數的方式，將個別效果視為截距。可寫成如下方程式：

\[ {{y}_{it}}=\alpha +\beta {{x}_{it}}+\mu \cdot {{D}_{i}}+{{\varepsilon }_{it}} \]
資料展開如圖 3.1中間的 \(D1,D2,..\) ，當 \(N\) 越多，\(D\) 內的向量就越多。這樣的做法，和單變數LS迴歸的原理完全一樣。所以，這樣就清楚了：因為估計個別效果用的資料是固定的虛擬變數，所以，這筆資料和解釋變數的關係是固定的。

knitr::include_graphics("images/3.1.png")
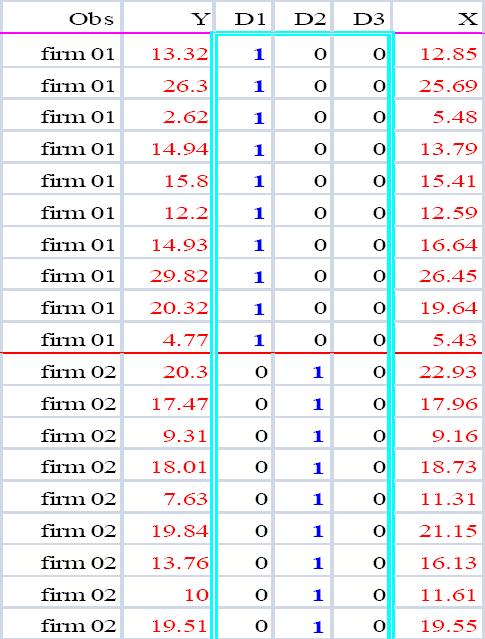
LSDV之資料結構

圖 3.1: LSDV之資料結構


接下來，我們用productivity.csv這筆資料以R來實做。如前面的解說，我們將配適美國48州生產毛額為6個變數所解釋的線性迴歸。這筆資料在研究美國各州的產出毛額(Gross State Products)和哪些因素有關。檔案內的數據都取了對數。下面的語法，承接前面載入的資料，我們就不重複指令

\[ {{y}_{it}}=a+{{b}_{1}}{{x}_{1it}}+{{b}_{2}}{{x}_{2it}}+\cdots +{{b}_{6}}{{x}_{6it}}+{{u}_{it}} \]
估計共同截距pool模型: 利用函數內的model = “pooling” 宣告pool model。 並將估計結果存入物件gsp_pool。下述程式同時利用了一些語法簡化複迴歸公式的人工輸入，就是Eq的產生，當自變數很多時或使用所有自變數時，讀者可以參考使用。 

temp1=read.csv("data/productivity.csv")
library(plm)
myData1=pdata.frame(temp1,index=c("state","year"))
dep= names(myData1)[3] 
indep= paste(names(myData1)[4:9], collapse="+")
Eq=paste(dep, indep, sep="~")
gsp_pool = plm(Eq, data = myData1, model = "pooling")
summary(gsp_pool)
## Pooling Model
## 
## Call:
## plm(formula = Eq, data = myData1, model = "pooling")
## 
## Balanced Panel: n = 48, T = 17, N = 816
## 
## Residuals:
##       Min.    1st Qu.     Median    3rd Qu.       Max. 
## -0.2377441 -0.0564618 -0.0035929  0.0489543  0.3331303 
## 
## Coefficients:
##               Estimate Std. Error t-value  Pr(>|t|)    
## (Intercept)  1.9260003  0.0525031 36.6836 < 2.2e-16 ***
## x1_hwy       0.0588882  0.0154114  3.8211 0.0001431 ***
## x2_water     0.1185816  0.0123566  9.5966 < 2.2e-16 ***
## x3_other     0.0085530  0.0123541  0.6923 0.4889360    
## x4_private   0.3120204  0.0110875 28.1417 < 2.2e-16 ***
## x5_emp       0.5496945  0.0155369 35.3800 < 2.2e-16 ***
## x6_unemp    -0.0072715  0.0013836 -5.2553 1.892e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Total Sum of Squares:    849.81
## Residual Sum of Squares: 5.9033
## R-Squared:      0.99305
## Adj. R-Squared: 0.993
## F-statistic: 19275 on 6 and 809 DF, p-value: < 2.22e-16


估計共同截距pool模型。利用函數內的model = “within” 宣告固定效果 model。並將估計結果存入物件gsp_fe物件

gsp_fe = plm(EQ, data = myData1, model = "within")
summary(gsp_fe)
## Oneway (individual) effect Within Model
## 
## Call:
## plm(formula = EQ, data = myData1, model = "within")
## 
## Balanced Panel: n = 48, T = 17, N = 816
## 
## Residuals:
##       Min.    1st Qu.     Median    3rd Qu.       Max. 
## -0.1207396 -0.0227308 -0.0013481  0.0184986  0.1546889 
## 
## Coefficients:
##               Estimate  Std. Error t-value  Pr(>|t|)    
## x1_hwy      0.07675220  0.03124370  2.4566   0.01425 *  
## x2_water    0.07869708  0.01500308  5.2454 2.023e-07 ***
## x3_other   -0.11477824  0.01814712 -6.3249 4.317e-10 ***
## x4_private  0.23498642  0.02621424  8.9641 < 2.2e-16 ***
## x5_emp      0.80117215  0.02975698 26.9238 < 2.2e-16 ***
## x6_unemp   -0.00517998  0.00097967 -5.2875 1.622e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Total Sum of Squares:    18.942
## Residual Sum of Squares: 1.03
## R-Squared:      0.94562
## Adj. R-Squared: 0.94184
## F-statistic: 2208.44 on 6 and 762 DF, p-value: < 2.22e-16


比較兩個模型，我們發現x3的估計值相差甚大：pool模型的係數是不顯著的正係數；fixed-effect模型的係數是顯著為負。
plm模組，提供6種模型處理個別效果設定：
model= c(“within”,“random”,….)
 within: 固定效果 (fixed-effect)
 random: 隨機效果(random-effect)，選擇隨機效果時，還必須宣告估計共變異數之權重矩陣 random.method，下一節會詳述。
 ht: Hausman and Taylor estimator，這是具內生性時所使用，後面會詳述。
 between: between estimator
 pooling: pooled OLS estimator
 fd: first–difference estimator

LSDV方法，雖然很簡單，但是實際上依然會遇到一些問題，例如：
 (1) LSDV須要估計截距，因此，當\(N\)很多但\(T\)少少時，會損失大量自由度。另外，隨然目前的PC很強大，\(N\)再大都處理的沒問題，但是，經過模擬實驗，\(N\)很大時，T也有一定的長度時，固定效果還是會當在那裡。和電腦硬碰硬的結果，可能不是很理想。第12章我們會介紹處理large panel的方法。
 (2) 太多虛擬變數，會惡化現有的線性重合問題。
 (3) LSDV估計固定效果，其實並不是估計固定效果對被解釋變數的影響；他只是將之透過\(Q \; transform\)移除。當一個研究想知道觀察不到的橫斷效果時，這個方法往往就不行。
 (4) Incidental parameter problem
這是一個最困擾Panel Data的理論問題。標準的Panel之漸進性質是來自 \(T\) 固定，\(N \to \infty\) 。所以，當 \(N\) 會增加時，固定效果對 \((a+ \mu_i)\) 的估計就不再是不偏的，只有解釋變數的係數 \(b\) 依然還是不偏的。雖然這是一個最困擾Panel Data的問題，但是，還好對 \(b\) 沒影響。

如果是使用MS-WORD寫文章的讀者，將估計結果的參數取出，存成表格再載入文件編輯，可以使用以下方法： 

write.csv(summary(gsp_fe)$coef, file= "table1.csv")


從專業的製表上看，語法第3行產生的係數估計值的中的Pr(>|z|)的數字過於冗長。於此介紹一個模組papeR內的函數prettify()，這個函數專門美化估計係數。但是在使用這個函數之前，必須將估計係數矩陣，轉成資料框架(data.frame)。如下兩行 

tabFE=as.data.frame(summary(gsp_fe)$coef)
knitr::kable(papeR:::prettify(tabFE))
Estimate Std. Error t-value Pr(>|t|)
x1_hwy 0.0767522 0.0312437 2.456566 0.014 *
x2_water 0.0786971 0.0150031 5.245396 <0.001 ***
x3_other -0.1147782 0.0181471 -6.324874 <0.001 ***
x4_private 0.2349864 0.0262142 8.964074 <0.001 ***
x5_emp 0.8011721 0.0297570 26.923841 <0.001 ***
x6_unemp -0.0051800 0.0009797 -5.287450 <0.001 ***

papeR:::prettify是不載入模組之下，呼叫模組 papeR 內的函數prettify()。上面output，雖然已經將Pr(>|z|)的數字管理好了，但是其他數值的小數位還是太多。我們可以在美化之前，先四捨五入，round(tabFE,4)，如下： 

papeR:::prettify(round(tabFE,4))
##              Estimate Std. Error t-value Pr(>|t|)    
## 1     x1_hwy   0.0768     0.0312  2.4566    0.014   *
## 2   x2_water   0.0787     0.0150  5.2454   <0.001 ***
## 3   x3_other  -0.1148     0.0181 -6.3249   <0.001 ***
## 4 x4_private   0.2350     0.0262  8.9641   <0.001 ***
## 5     x5_emp   0.8012     0.0298 26.9238   <0.001 ***
## 6   x6_unemp  -0.0052     0.0010 -5.2875   <0.001 ***


這樣的表格看起來就好多了。

 估計方法 2. GLS (Generalized Least Square)
第2個固定效果估計方法是GLS。當殘差項不再是\(i.i.d.\)的時候，一則是自己有序列相關(serial correlation)，一則是殘差之間有特定的相關性，類似SUR (seemingly unrelated regression)的狀況。Panel Data之殘差之間產生有四種基本互相關連：
  (1) Cross-section specific heteroskedasticity
  (2) Period specific heteroskedasticity
  (3) Contemporaneous covariances (cross-section SUR)
  (4) Between period covariances.

此時，LSDV之LS就不再適用Eq.(3.3)的估計，可以使用一般化的逆矩陣(generalized inverse)在GLS架構下估計，也會得到具BLUE性質的參數。令\(\Omega_u\) 為一般化的殘差矩陣，此時Eq.(3.4) 的GLS如下

\[ \tag{3.7} {{\tilde{b }}_{GLS}}={{\left( \mathbf{{X}'{Q}'}\Omega _{u}^{-1}\mathbf{QX} \right)}^{-1}}\mathbf{{X}'{Q}'}\Omega _{u}^{-1}\mathbf{Q}{{y}_{t}} \] 上式中的殘差如果未知，則使用feasible GLS，原理是在演算法上，利用recursive估計未知殘差。一般通稱就是用FGLS。FGLS可以用在pooled OLS和固定效果。plm模組內的函數pggls()提供了這項演算。

FGLS估計pooled OLS的R Code如下

gsp_poolFGLS=pggls(Eq, data = myData1, model = "pooling")
summary(gsp_poolFGLS)
## Oneway (individual) effect General FGLS model
## 
## Call:
## pggls(formula = Eq, data = myData1, model = "pooling")
## 
## Balanced Panel: n = 48, T = 17, N = 816
## 
## Residuals:
##     Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
## -0.25591 -0.07142 -0.01978 -0.01202  0.03591  0.42502 
## 
## Coefficients:
##                Estimate  Std. Error  z-value  Pr(>|z|)    
## (Intercept)  2.38461491  0.09305164  25.6268 < 2.2e-16 ***
## x1_hwy       0.07266315  0.01977556   3.6744 0.0002384 ***
## x2_water     0.06853508  0.01149780   5.9607 2.511e-09 ***
## x3_other    -0.00608318  0.01530225  -0.3975 0.6909729    
## x4_private   0.21510388  0.01498942  14.3504 < 2.2e-16 ***
## x5_emp       0.68531349  0.01911145  35.8588 < 2.2e-16 ***
## x6_unemp    -0.00485120  0.00047762 -10.1570 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Total Sum of Squares: 849.81
## Residual Sum of Squares: 7.174
## Multiple R-squared: 0.99156

FGLS估計固定效果的R Code如下

gsp_feFGLS=pggls(Eq, data = myData1, model = "within")
summary(gsp_feFGLS)
## Oneway (individual) effect Within FGLS model
## 
## Call:
## pggls(formula = Eq, data = myData1, model = "within")
## 
## Balanced Panel: n = 48, T = 17, N = 816
## 
## Residuals:
##         Min.      1st Qu.       Median      3rd Qu.         Max. 
## -0.113826759 -0.023679043 -0.003690021  0.017149550  0.170514608 
## 
## Coefficients:
##               Estimate  Std. Error z-value  Pr(>|z|)    
## x1_hwy      0.02668604  0.03481065  0.7666  0.443316    
## x2_water    0.03961562  0.01329854  2.9789  0.002892 ** 
## x3_other   -0.05191236  0.01996699 -2.5999  0.009325 ** 
## x4_private  0.13191101  0.01690482  7.8032 6.038e-15 ***
## x5_emp      0.87372428  0.02073304 42.1416 < 2.2e-16 ***
## x6_unemp   -0.00365546  0.00048283 -7.5709 3.706e-14 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Total Sum of Squares: 849.81
## Residual Sum of Squares: 1.1211
## Multiple R-squared: 0.99868

有關美化表格所需要的呼叫的係數估計矩陣coef，plm的物件寫的有一些不一致。前面用小寫，GLS估計結果則呼叫係數估計矩陣時是用Coef，i.e.參數第一的字母必須大寫。如下，其餘套用皆一樣。如下：

summary(gsp_feFGLS)$Coef
##                Estimate   Std. Error    z-value     Pr(>|z|)
## x1_hwy      0.026686041 0.0348106550  0.7666055 4.433161e-01
## x2_water    0.039615616 0.0132985424  2.9789442 2.892434e-03
## x3_other   -0.051912359 0.0199669927 -2.5999088 9.324855e-03
## x4_private  0.131911008 0.0169048221  7.8031586 6.037659e-15
## x5_emp      0.873724276 0.0207330386 42.1416413 0.000000e+00
## x6_unemp   -0.003655463 0.0004828294 -7.5709201 3.705900e-14


3.2 隨機效果


隨機效果指 \(\mu_i\) 解釋變數 \(X\) 間的相關性是隨機的，隨機意味「時有相關，時無相關」，千萬別理解成stochastic。由上面介紹可以知道，固定效果需估計的參數很多，這會讓研究者的資料損失大量自由度。隨機效果則可以避免這樣的問題，但是，何時隨機效果是一個合理的選擇？前面的權重矩陣含有的資訊是 \(N\) 筆殘差序列的相互關係，隨機效果的假設則是，在於將\(\mu_i\) 視為是第 \(i\) 個樣本群的一筆隨機變數；也就是可將之視為類似殘差項，且每個 \(i\) 在不同時點的抽樣皆為固定。在隨機效果假設之下，則用GLS 和MLE(最大概似法)皆可以。隨機效果之下的GLS和前面的不同，主要差異在隨機效果須要基本分配假設。

 估計方法 1: GLS
已知一個panel data 迴歸 \({{y}_{it}}=a+b{{x}_{it}}+\left( {{\mu }_{i}}+{{\varepsilon }_{it}} \right)\) ，隨機效果GLS有如下假設：
\(E[\text{ }{{\varepsilon }_{it}}]=0 \\ E[{{\mu }_{i}}]=0 \\ E[{{\varepsilon }_{it}}{{\mu }_{j}}]=0\)
\(E[\varepsilon _{it}^{2}]=\sigma _{\varepsilon }^{2} \\ E[\mu _{it}^{2}]=\sigma _{\mu }^{2}\)
\(E[{{\varepsilon }_{it}}{{\varepsilon }_{js}}]=0, \;s\ne t\)
\(E[{{\mu }_{i}}{{\mu }_{j}}]=0,\;i\ne j\)
故如同一般GLS的觀念，就是一個內插逆矩陣的做法，結果如下：

\[ \tag{3.8} {{\tilde{b}}_{GLS}}={{\left( \mathbf{{X}'}\Omega _{\mu ,\varepsilon }^{-1}\mathbf{X} \right)}^{-1}}\mathbf{{X}'}\Omega _{\mu ,\varepsilon }^{-1}{{y}_{t}} \] Eq.(3.8)內

\[ \tag{3.9} {{\Omega }_{\mu ,\varepsilon }}={{\text{I}}_{\text{N}}}\otimes {{\Sigma }_{\mu ,\varepsilon }}=\sigma _{\mu }^{2}\left( {{\text{I}}_{\text{N}}}\otimes {{\text{J}}_{\text{N}}} \right)+\sigma _{\varepsilon }^{2}\left( {{\text{I}}_{\text{N}}}\otimes {{\text{I}}_{\text{T}}} \right) \]
且
\[ \tag{3.10} {{\Sigma }_{\mu ,\varepsilon }}=\left[ \begin{matrix} \sigma _{{{\mu }_{1}}}^{2}+{{\sigma }_{\varepsilon ,11}} & {{\sigma }_{\varepsilon ,12}} & \cdots & {{\sigma }_{\varepsilon ,1N}} \\ {{\sigma }_{\varepsilon ,21}} & \sigma _{{{\mu }_{2}}}^{2}+{{\sigma }_{\varepsilon ,22}} & \cdots & \sigma _{\varepsilon }^{2} \\ \vdots & \vdots & \ddots & \vdots \\ {{\sigma }_{\varepsilon ,N1}} & {{\sigma }_{\varepsilon ,N2}} & \cdots & \sigma _{{{\mu }_{1}}}^{2}+{{\sigma }_{\varepsilon ,NN}} \\ \end{matrix} \right] \]
如果假設同質變異，則
\[ \tag{3.11} {{\Sigma }_{\mu ,\varepsilon }}=\left[ \begin{matrix} \sigma _{\mu }^{2}+\sigma _{\varepsilon }^{2} & \sigma _{\varepsilon }^{2} & \cdots & \sigma _{\varepsilon }^{2} \\ \sigma _{\varepsilon }^{2} & \sigma _{\mu }^{2}+\sigma _{\varepsilon }^{2} & \cdots & \sigma _{\varepsilon }^{2} \\ \vdots & \vdots & \ddots & \vdots \\ \sigma _{\varepsilon }^{2} & \sigma _{\varepsilon }^{2} & \cdots & \sigma _{\mu }^{2}+\sigma _{\varepsilon }^{2} \\ \end{matrix} \right] \]
對照Eq.(3.5)的 \(Q\) 轉換，隨機效果則是 \(\Omega^{-1}\) 轉換。隨機效果估計原理的技術細節較為繁瑣， 一書, 如果是第7版，在第11章第5節。估計的概念， 簡略說明如下：
  (1) 當變異數矩陣已知：GLS (Generalized LS)
用已知變異數對LS加權(weighting)的估計式。
  (2) 當變異數矩陣未知：FGLS (Feasible GLS)
先估計一個一致變異數(consistent covariance)，再用之對LS加權的估計式。

隨機效果的GLS估計，R程式如下

gsp_re = plm(Eq, data = myData1, model = "random", random.method = "walhus")
summary(gsp_re)
## Oneway (individual) effect Random Effect Model 
##    (Wallace-Hussain's transformation)
## 
## Call:
## plm(formula = Eq, data = myData1, model = "random", random.method = "walhus")
## 
## Balanced Panel: n = 48, T = 17, N = 816
## 
## Effects:
##                    var  std.dev share
## idiosyncratic 0.001530 0.039116 0.211
## individual    0.005704 0.075527 0.789
## theta: 0.8754
## 
## Residuals:
##       Min.    1st Qu.     Median    3rd Qu.       Max. 
## -0.1077901 -0.0247596 -0.0014392  0.0207172  0.1833187 
## 
## Coefficients:
##                Estimate  Std. Error z-value  Pr(>|z|)    
## (Intercept)  2.15001436  0.13401683 16.0429 < 2.2e-16 ***
## x1_hwy       0.06103115  0.02139204  2.8530  0.004331 ** 
## x2_water     0.07606342  0.01390984  5.4683 4.543e-08 ***
## x3_other    -0.09395406  0.01692541 -5.5511 2.839e-08 ***
## x4_private   0.27887470  0.01940812 14.3690 < 2.2e-16 ***
## x5_emp       0.73851275  0.02468806 29.9138 < 2.2e-16 ***
## x6_unemp    -0.00607310  0.00088786 -6.8402 7.909e-12 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Total Sum of Squares:    31.848
## Residual Sum of Squares: 1.1319
## R-Squared:      0.96446
## Adj. R-Squared: 0.9642
## Chisq: 21953.5 on 6 DF, p-value: < 2.22e-16


估計隨機效果，R提供4個GLS用的權重矩陣： “swar” (內定), “walhus”, “amemiya” 和 “nerlove”。swar就是Swamy-Arora估計式；walhus是Wallace-Hussain估計式。後面兩個是工具變數估計隨機效果模型所使用。
另外，雖然函數pggls()可以選擇估計隨機效果設定，如下：

pggls(formula = Eq, data = myData1, model = "random", random.method = "swar")
估計結果其實和用GLS估計Pooled OLS是一樣的。這個結果的x3係數，和前面pooled OLS一樣。但是這個問題，使用隨機效果權重就沒問題了。關鍵在於 pggls() 無法使用這個指令 random.method = "swar"，就算寫入也沒有用。



 估計方法2：MLE最大概似法 最大概似法需要對殘差項的分配做假設。假設其為常態分配時，其概似函數如下：
\[ \tag{3.12} \begin{align} & L(a,b,{{\varphi }^{2}},\sigma _{\varepsilon }^{2})= \text{constant}-NT\log {{\sigma }_{\varepsilon }}+N\log \varphi -\frac{1}{2\sigma _{\varepsilon }^{2}}{u}'{{\Sigma }^{-1}}u \\ \end{align} \]
where \(\Omega =\sigma _{\varepsilon }^{2}\Sigma \\ \Sigma =Q+\frac{P}{{{\varphi }^{2}}}\) 和
\({{\varphi }^{2}}=\frac{\sigma _{\varepsilon }^{2}}{\sigma _{1}^{2}}\) 另外，
\(\left| \Omega \right|={{(\sigma _{\varepsilon }^{2})}^{N(T-1)}}{{(\sigma _{1}^{2})}^{N}}={{(\sigma _{\varepsilon }^{2})}^{NT}}{{({{\varphi }^{2}})}^{-N}}\)


解 Eq.(3.12)的方法之一，就是使用數值方法，直接演算其最大概似值求取參數。但是 Amemiya (1971) 指出，這樣會導致非線性一階條件。在線性模型出現非線性一階條件，會導致求解Global Maximum變的困難。
因此，Breusch (1987) 提出了一些避免求解時落入local miximum的陷阱，就是藉助固定效果 within 和 between 兩個估計式作為遞迴運算的輔助。這裡許多細節需要的代數結構太繁瑣，有興趣的讀者，可以參考兩篇原始論文與 Maddala (1971) 的經典討論。
R的部份，則無法使用模組 plm，我們將使用R的內建估計線性混和效果(linear mixed-effect)的函數 lme()。lme()這個函數，是R內建模組 nlme，所以使用時，不需要載入模組。R啟動時，就會自動載入。這個模組有相當進階的非線性模型，可以用以估計panel data之下的二元乃至各種非線性間斷機率模式。 

gsp_reML=nlme::lme(as.formula(Eq),data=temp1,random=~1|state)
summary(gsp_reML)
## Linear mixed-effects model fit by REML
##   Data: temp1 
##        AIC       BIC   logLik
##   -2787.69 -2745.428 1402.845
## 
## Random effects:
##  Formula: ~1 | state
##         (Intercept)   Residual
## StdDev:  0.08987078 0.03680898
## 
## Fixed effects:  as.formula(Eq) 
##                  Value  Std.Error  DF   t-value p-value
## (Intercept)  2.1783595 0.14938903 762 14.581790  0.0000
## x1_hwy       0.0628585 0.02292175 762  2.742307  0.0062
## x2_water     0.0754364 0.01404131 762  5.372463  0.0000
## x3_other    -0.1009956 0.01716109 762 -5.885150  0.0000
## x4_private   0.2693669 0.02085568 762 12.915757  0.0000
## x5_emp       0.7557325 0.02577602 762 29.319215  0.0000
## x6_unemp    -0.0057849 0.00089791 762 -6.442619  0.0000
##  Correlation: 
##            (Intr) x1_hwy x2_wtr x3_thr x4_prv x5_emp
## x1_hwy     -0.729                                   
## x2_water    0.168  0.016                            
## x3_other    0.012 -0.364 -0.142                     
## x4_private -0.502 -0.027 -0.336  0.051              
## x5_emp      0.494 -0.196 -0.217 -0.401 -0.606       
## x6_unemp    0.424 -0.142 -0.143 -0.222 -0.399  0.534
## 
## Standardized Within-Group Residuals:
##        Min         Q1        Med         Q3        Max 
## -3.1963754 -0.6219418 -0.0394193  0.4869007  4.1537513 
## 
## Number of Observations: 816
## Number of Groups: 48


summary(gsp_reML)$tTable
##                    Value    Std.Error  DF   t-value       p-value
## (Intercept)  2.178359517 0.1493890339 762 14.581790  1.165581e-42
## x1_hwy       0.062858470 0.0229217481 762  2.742307  6.244089e-03
## x2_water     0.075436432 0.0140413115 762  5.372463  1.032747e-07
## x3_other    -0.100995609 0.0171610925 762 -5.885150  5.956589e-09
## x4_private   0.269366853 0.0208556766 762 12.915757  1.187408e-34
## x5_emp       0.755732527 0.0257760153 762 29.319215 4.292906e-127
## x6_unemp    -0.005784884 0.0008979088 762 -6.442619  2.080133e-10


summary(gsp_reML)$logLik
## [1] 1402.845


summary(gsp_reML)$AIC
## [1] -2787.69


summary(gsp_reML)$BIC
## [1] -2745.428


summary(gsp_reML)$coef$random
## $state
##      (Intercept)
## 1  -0.1308619791
## 2   0.0387526324
## 3  -0.0303404760
## 4   0.1106973736
## 5   0.0363469261
## 6   0.1001033220
## 7   0.1391623627
## 8  -0.0322155953
## 9  -0.0738272598
## 10  0.0322607008
## 11  0.0047075227
## 12 -0.0772453994
## 13 -0.0528459034
## 14 -0.0193152914
## 15  0.0186416659
## 16  0.1554067985
## 17 -0.1019342134
## 18  0.0105125814
## 19  0.0489672821
## 20  0.0103173548
## 21 -0.0729269796
## 22 -0.0686854287
## 23 -0.0540234100
## 24 -0.0241390141
## 25  0.0138338880
## 26  0.0185932878
## 27 -0.0157457892
## 28  0.0684231351
## 29  0.1087596279
## 30  0.1166637061
## 31 -0.1144385293
## 32 -0.0009390054
## 33 -0.0826019103
## 34  0.0786537035
## 35 -0.0206257253
## 36 -0.0852076162
## 37  0.0492616634
## 38 -0.2029098258
## 39 -0.0519998692
## 40 -0.1342784044
## 41 -0.0015866501
## 42  0.0335657403
## 43 -0.0208707644
## 44 -0.0240216436
## 45  0.1140526477
## 46 -0.0550368343
## 47 -0.0521666751
## 48  0.2931062702


對於MLE的估計，我們先說明這個函數
lme(as.formula(Eq),data=temp1,random=~1|state)
這個函數的使用相當簡單，要注意3個條件的宣告：
 第1、因為lme()函數不做as.formula處理方程式字串。必需如上述Code Chunk方式宣告。
 第2、資料不能宣告具有 panel data 結構的myData1，因為lme()這不是 plm 內的估計函數，所以，不能放它種資料結構。
 第3、random=~1|state 宣告隨機效果的維度在哪裡，如果要雙維， 也相當方便。這個函數，可以處理多層次panel data以及修正序列相關， 第四章雙維隨機效果， 和第五章尾我們還會再使用到。

可以執行 names(summary(gsp_reML)) 知道內有多少物件在內。如下： 

names(summary(gsp_reML))
##  [1] "modelStruct"  "dims"         "contrasts"    "coefficients" "varFix"      
##  [6] "sigma"        "apVar"        "logLik"       "numIter"      "groups"      
## [11] "call"         "terms"        "method"       "fitted"       "residuals"   
## [16] "fixDF"        "na.action"    "data"         "corFixed"     "tTable"      
## [21] "BIC"          "AIC"

上面MLE的結果，可以和前面GLS的結果比較一番。GLS需要權重，MLE較為簡單，且可以修正複雜的資料問題，以及多個橫斷面個別效果。

References

Amemiya, Takeshi. 1971. “The Estimation of the Variances in a Variance-Components Model.” International Economic Review 12 (1): 1–13. https://doi.org/10.2307/2525492.
Breusch, Trevor S. 1987. “Maximum Likelihood Estimation of Random Effects Models.” Journal of Econometrics 36 (3): 383–89. https://doi.org/https://doi.org/10.1016/0304-4076(87)90010-8.
Maddala, G. S. 1971. “The Use of Variance Components Models in Pooling Cross Section and Time Series Data.” Econometrica 39 (2): 341–58. https://doi.org/10.2307/1913349.