第 1 章 線性模型與最小平方法估計原理
R的panel data模組是 plm, 這個模組承接多數R的線性模式 lm() 函數的使用方法。 本章就用lm()的介紹,來介紹R的函數和特徵。第2部份,因為牽涉到時間序列和單根檢定,所以,也先用這種方式介紹panel unit root。這樣,讀者在使用R上,比較能夠滿足相關資料分析需求。 以免介紹一堆與panel 無直接關的語法和指令。
假設我們有兩筆資料,分別為x和y,其散佈如圖 1.1:
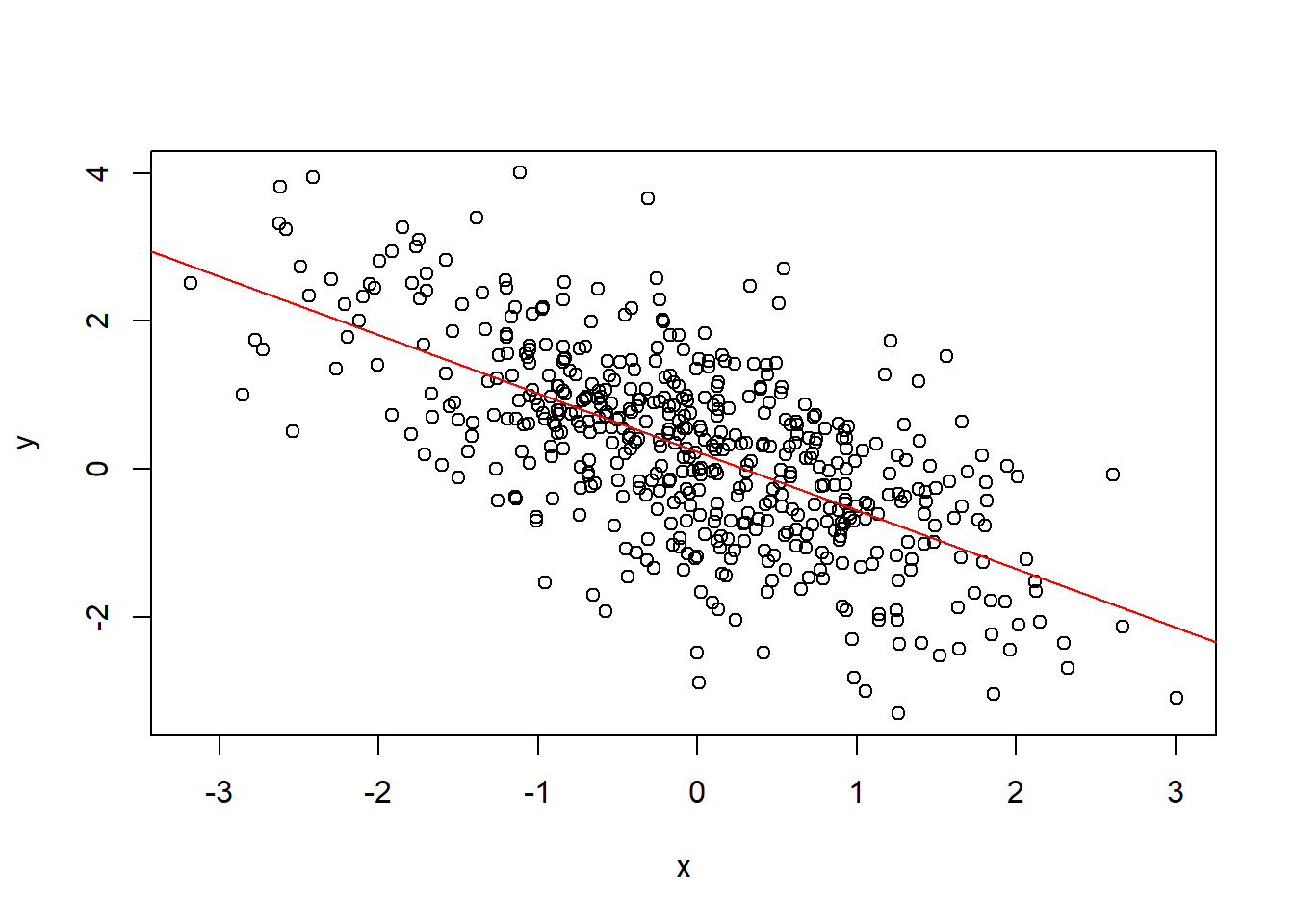
圖 1.1: 資料散佈圖
視覺上可以知道兩者之間為負相關,因此,我們可以目測:用尺在差不多的地方畫一條負斜率的直線,如上圖之斜截式。上圖之直線,稱為配適線(fitted line), 散佈之樣本和這條線的距離稱為殘差或剩餘(residuals)。理論上,一條直線可以寫成斜截式,如下:
\[ \tag{1.1} y=\alpha+ \beta X+ \varepsilon \]
已知一隨機變數\(X\) ,一個看上式 \(y\) 的理論角度是資料生成過程(DGP, data
generating process), \(y\) 是被以下三個成份所生成:
固定常數\(\alpha\) ;
\(X\) 的線性組合 \(\beta X\);
具備 \(i.i.d\) 性質的隨機干擾項 \(\varepsilon, \varepsilon \sim IID(0,\sigma^2)\)。
在DGP中,\(y\) 是被右式所生成,是一個純粹的被解釋變數,這是理論世界才會有的完美性質。
在不完美的經驗(樣本)世界中,我們觀察到\(y\),並假設\(y\) 是被 \(X\) 的線性DGP;因此,透過 \(y\) 和 \(X\) 的樣本資料,我們用下式去捕捉以上DGP的關係
\[
\tag{1.2A}
y=a+bX+e
\]
右邊之 \(a+bX\) 也稱為 \(y\) 的條件期望值,通常寫成 \(E[y|X]\) 或 \(\hat y\),
\(e\) 則為估計誤差(estimation errors)。Eq.(1.2A)的工作是基於樣本資料,
故也稱為樣本迴歸分析(sample regression
analysis);同理,我們可以將Eq.(1.1)的DGP視為理論或母體性質。
一言以蔽之,實證分析的方法論就是認為 \([a, b]\) 是\([\alpha,\beta]\)
的樣本估計值, 最小平方法(Least Square, LS)估出來的\([a, b]\)則是
\([\alpha,\beta]\) 的最佳估計式。
Eq.(1.1)中,\(y\) 和\(X\) 的關係是事先的,生成的。Eq.(1.2A)中,\(y\) 和\(X\) 的關係是事後的,迴歸的。這種關係就像極值檢定:理論上,我們可以預設一個具有極值的函數\(y=f(X)\),然後,確定極大(小)值的周邊性質;實際上,我們不知道函數\(y\) 有哪一種極值,因此,就須要檢定(test)這些周邊性質。
迴歸分析也是這樣,Eq.(1.2A)中,\(y\) 和
\(X\) 的關係是否來自Eq.(1.1),就須要一些條件的支持與驗證,例如:不偏,參數顯著性,模型配適程度等等。本書就不深入涉及計量理論的細節,我們從資料的角度認識計量分析即可。
迴歸分析第一件工作就是「估計」:用數理方法估計出這一條線的截距和斜率(統稱參數或係數),而不是用目測。對於線性關係的估計,最好的方法就是最小平方法,這個方法求解參數的目標函數為:使估計殘差平方和為最小的參數集合。
Eq.(1.2A)的最小平方法之解為:
\[
\tag{1.2B}
b_{LS}=\frac{\sum\limits_{i=1}^{n}{({{X}_{i}}-\bar{X})({{y}_{i}}-\bar{y})}}{\sum\limits_{i=1}^{n}{{{({{X}_{i}}-\bar{X})}^{2}}}}
\]
在多變數複迴歸時,往往要利用矩陣,Eq.(1.1)可以寫成
\[
y=X \beta+ \varepsilon
\]
一個標準的線性迴歸則可以矩陣表示如下:
\[
y=Xb+ e
\]
上式中
\(y\) 為觀察值為 \(n\) 的被解釋變數(或稱為 \(n \times 1\) 的向量).
\(X\) 是解釋變數,假設有 \(k\) 個,故 \(X\) 為 \(n \times k\) 的獨立資料矩陣.
循上可知 \(b\) 為 \(k-\)
維的係數向量。 \(e\) 假設為 \(i.i.d\) 估計誤差,也就是變數 \(y\) 的變異,被 \(Xb\) 變異解釋後的剩餘。
令\(b\) 代表 \(\beta\) 的樣本估計式,則滿足下式的解,即為迴歸係數
\[
\underset{b}{\mathrm{min}} \; e'e=(y-Xb)'(y-Xb)
\]
上述目標函數,即是「殘差的平方和」,以偏微分解出最適值如下:
\[
\tag{1.3}
b_{LS}=(X'X)^{-1}X'y
\]
這個迴歸係數估計式的共變異數矩陣(covariance matrix)的式子為
\[
\tag{1.4}
cov(b)=s^{2}(X'X)^{-1}X'y
\]
Eq.(1.4)中,\(s^{2}=\frac{e'e}{n-k}\) , \(e=y-Xb\) 。因為有 \(k\) 個係數,所以 \(cov(b)\) 為 \(k \times k\) 方陣。如下
\[
\begin{equation}
\tag{1.5}
cov(b) =
\begin{pmatrix}
s_{11} & s_{12} & \cdots & s_{1k} \\
s_{21} & s_{22} & \cdots & s_{2k} \\
\vdots & \vdots & \ddots & \vdots \\
s_{k1} & s_{k2} & \cdots & s_{kk}
\end{pmatrix}
\end{equation}
\]
Eq.(1.5)中,主對角線 (main diagonal) 第 \(k\) 個數值,
就是係數自己的變異數,取根號後,就是標準差,可以用來檢定個別參數的性質,好比是否顯著異於0。離對角線(off-diagonal)就是交叉成分\(s_{ij}\) ,為參數間的共變異。 可以用來檢定參數間的關係、 相關性等結合檢定(joint tests)。後續會繼續說明。
1.1 單變數線性迴歸
我們先打開資料IS_CA.csv這個檔案,這個檔案是全球140個國家1980-2010年的平均資料,這筆資料是橫斷面資料。變數定義如下:
INVEST=投資率 (投資毛額/GNP)
SAVING=儲蓄率(儲蓄毛額/GNP)
CA=經常帳餘額(經常帳/GNP)
Countries=國名
Group=經濟發展程度分類
看看6筆觀察值:
## INVEST SAVING CA Countries Group
## 1 19.31094 16.33861 -2.665774 United States Advanced Economies
## 2 21.79923 22.40319 1.838452 Germany Advanced Economies
## 3 19.91765 20.43074 0.108710 France Advanced Economies
## 4 21.36210 20.27503 -0.874806 Italy Advanced Economies
## 5 24.29903 21.33197 -2.966290 Spain Advanced Economies
## 6 21.07326 25.89884 4.825516 Netherlands Advanced Economies再看一下基本統計摘要:
## INVEST SAVING CA Countries
## Min. : 6.992 Min. :-16.11 Min. :-24.0701 Albania : 1
## 1st Qu.:20.570 1st Qu.: 16.00 1st Qu.: -5.5788 Algeria : 1
## Median :23.546 Median : 20.35 Median : -2.9622 Antigua and Barbuda: 1
## Mean :23.919 Mean : 20.38 Mean : -1.7747 Argentina : 1
## 3rd Qu.:26.425 3rd Qu.: 24.67 3rd Qu.: 0.1403 Armenia : 1
## Max. :43.372 Max. : 43.10 Max. :122.9456 Australia : 1
## NA's :14 NA's :14 (Other) :134
## Group
## Advanced Economies :34
## Central and Eastern Europe :14
## Commonwealth of Independent States:13
## Developing Asia :27
## Latin America and the Caribbean :32
## Middle East and North Africa :20
##
summary(temp)是資料的摘要,不是較詳細的敘述統計量。但是,對於資料的狀況、分佈和缺值等等,都有重要資訊。例如,Countries和Group均是文字,比對的數據,其實就告訴了我們,不同經濟發展程度下有多少國家。例如,Advanced
Economies有34國。 如果需要進一步較詳細的統計資訊,basicStats()
可以計算16項數據和資料的性質,這個函數只能用於實數資料的統計計算,所以,我們的資料只有前3欄是數字,所以,就用1:3取前3行。
library(fBasics)
myData=na.omit(temp) # 移除缺值(na.omit()是將缺值移除的函數)
basicStats(myData[,1:3]) #前3筆連續資料的16項統計摘要## INVEST SAVING CA
## nobs 126.000000 126.000000 126.000000
## NAs 0.000000 0.000000 0.000000
## Minimum 6.992129 -16.107180 -24.070130
## Maximum 43.372190 43.101810 23.996190
## 1. Quartile 20.569858 16.004915 -5.661331
## 3. Quartile 26.425002 24.668167 0.020863
## Mean 23.918973 20.382678 -3.075776
## Median 23.546400 20.354840 -2.962245
## Sum 3013.790579 2568.217445 -387.547744
## SE Mean 0.488447 0.711381 0.612932
## LCL Mean 22.952276 18.974766 -4.288844
## UCL Mean 24.885669 21.790590 -1.862707
## Variance 30.061087 63.763982 47.336380
## Stdev 5.482799 7.985235 6.880144
## Skewness 0.634276 -0.420341 0.182746
## Kurtosis 1.592273 2.934852 2.273181
R資料格式,基本的有兩種:向量矩陣(vector/matrix)和資料框架(data.frame)。都是用矩陣列\(\times\)行的方式,呼叫部份資料。例如,myData[1:2, 2:3]
就是呼叫資料前2列和後2行。下面兩個語法,呼叫同樣的結果。
basicStats(myData[,1:3])["Sum", ]
basicStats(myData[,1:3])[9, ]
一些常用的敘述統計摘要:
## INVEST SAVING CA
## 23.918973 20.382678 -3.075776## INVEST SAVING CA
## 23.918973 20.382678 -3.075776## INVEST SAVING CA
## 0.6342756 -0.4203411 0.1827463
## attr(,"method")
## [1] "moment"## INVEST SAVING CA
## 1.592273 2.934852 2.273181
## attr(,"method")
## [1] "excess"## INVEST SAVING CA
## INVEST 30.061087 20.61680 -4.434602
## SAVING 20.616802 63.76398 38.126174
## CA -4.434602 38.12617 47.336380## INVEST SAVING CA
## INVEST 30.061087 20.61680 -4.434602
## SAVING 20.616802 63.76398 38.126174
## CA -4.434602 38.12617 47.336380## INVEST SAVING CA
## INVEST 1.0000000 0.4709028 -0.1175587
## SAVING 0.4709028 1.0000000 0.6939657
## CA -0.1175587 0.6939657 1.0000000
其次,我們執行單變數線性迴歸
\[ INVEST=a+b_{1} \times SAVING +e \]
這筆資料的投資率,是固定資本形成毛額。這個迴歸可以評估一個國家「儲蓄率」對「投資率」的關係,係數b1也稱為儲蓄保留係數(saving retention coefficient)衡量了儲蓄對投資的貢獻。依照經濟學原理,這個迴歸係數有兩種可能:
其一、如果是國際資本流動高程度高的封閉體系,則應該是顯著正相關,以反映出整體儲蓄對整體投資的正面誘因。然而,我們還可以看一看相關程度和影響有多大。
其二、如果是國際資本流動高程度高的開放體系,則應該是不顯著正相關,反映出國內投資所需資本,在國際資本市場上融資,所以,國內投資和國內儲蓄沒有統計上的相關性。這就是著名的 Feldstein and Horioka (1980) 對國際資本研究(International Capital Mobility)的議題,也是著名的國際資本流動迷思(Puzzle)。
估計線性迴歸
##
## Call:
## lm(formula = INVEST ~ SAVING, data = myData)
##
## Residuals:
## Min 1Q Median 3Q Max
## -13.265 -3.330 -1.145 2.867 17.766
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 17.3286 1.1902 14.560 < 2e-16 ***
## SAVING 0.3233 0.0544 5.944 2.63e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.856 on 124 degrees of freedom
## Multiple R-squared: 0.2217, Adjusted R-squared: 0.2155
## F-statistic: 35.33 on 1 and 124 DF, p-value: 2.627e-08
這個估計結果摘要的output,有幾項可以注意,爾後本書簡單的列出結果。例如,Call是估計函數,殘差的分量用來檢視離群值的狀況。Signif. codes
指稱顯著性。最下方則是基礎F檢定。由以上結果,我們發現兩者是正相關,估計出之係數為0.323,由極小之P-value,可知其非常顯著。一般解釋這個係數的方式為:其他條件不變,
這樣的解讀只是針對那條斜截式產生的直線,而沒有解釋其統計意涵。畢竟迴歸方法估計出來的直線,其解讀必須依照所產生的方法。這個數字的統計解釋如下:其他條件不變,
說明如下,根據Eq.(1.2B)的解:\(X\) 高於 \(\bar X\) 1單位,意味 \((X_i - \bar X)=1\) ,也就是分母等於 \(n\)
\[ 0.323 = \frac{\sum\limits_{i=1}^{n}{(1)({{y}_{i}}-\bar{y})}} {\sum\limits_{i=1}^{n}{(1)}} \]
故 \[ 0.323 =\frac{\sum\limits_{i=1}^{n}{({{y}_{i}}-\bar{y})}}{n} \]
根據上式,估計係數的解讀就是:
這個結果對於統計決策十分有用。它將相對變化定位於平均數,因此,決策考慮的就是目前要如何對照平均數相對調整。所以,線性模型雖然簡單,但是,對於制訂決策十分好用。複雜的演算法模型,往往無法告訴你決策參照點是那個數字。
因為這筆資料不是時間序列。所以在解釋變動時,要強調樣本間差異,而不是成長率。如果是時間數列,則可以用具有時間趨勢意涵的成長率來解釋。
如果覺得小數點顯示非0位數太多,要改成至少4個有意義的非0數字,可以執行options(digits = 4)1修改。如果要四捨五入,則可以用函數round(),以此例,round(FH_1vlm, 3)將故計數據,近似到小數第3位。
lm()還有2個重要的指令:
第1。如果解釋變數很多,要將資料所有的變數都放進去,則
lm(y ~ ., data=)
這個功能就很有用。 第2。如果要去除截距,則在解釋變數後面增加
-1,如下:
lm(INVEST~SAVING-1, data=myData)
summary()和confint()是兩個處理迴歸後物件FH_1vlm的底層函數 (Base R functions),詳細的底層函數後面會列表說明。
只要係數表,則
| Estimate | Std. Error | t value | Pr(>|t|) | ||
|---|---|---|---|---|---|
| (Intercept) | 17.329 | 1.190 | 14.560 | <0.001 | *** |
| SAVING | 0.323 | 0.054 | 5.944 | <0.001 | *** |
迴歸係數90%之信任區間
## 5 % 95 %
## (Intercept) 15.3562912 19.3009961
## SAVING 0.2331837 0.4134761
令\(\mathrm{SE}(b_{1})\) 代表估計係數\(b_{1}\) 的標準誤差(standard
errors),信任區間的定義:
\[
b_{1} \pm 2\ \cdot \ \mathrm{SE}(b_{1})
\]
這個信任區間,將
\(\alpha=10%\) 分成一半一半,兩端各5%。利用這些資訊,我們可以繪出intercept
和 SAVING 兩個係數的信任橢圓 (confidence
ellipse),下面的程式檔, 說明了如何繪製係數的信任橢圓。
##
## Attaching package: 'ellipse'## The following object is masked from 'package:graphics':
##
## pairsplot(ellipse(FH_1vlm,c(1,2)),type="l")
points(coef(FH_1vlm)[1], coef(FH_1vlm)[2], pch=13)
abline(v=confint(FH_1vlm)[1,], lty=2)
abline(h=confint(FH_1vlm)[2,], lty=2)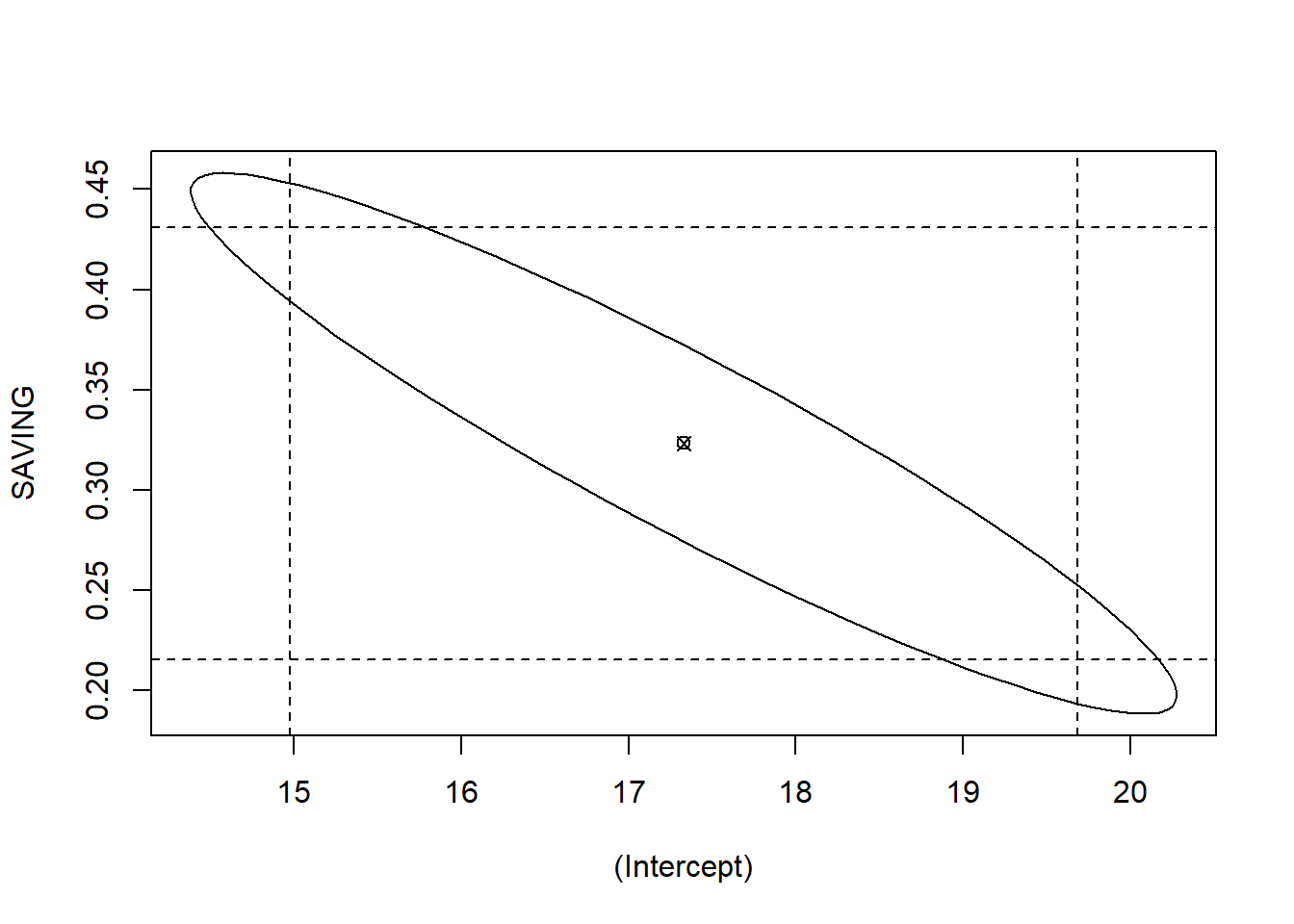
圖 1.2: 信任橢圓
圖1.2的橢圓面積內,沒有座標(0,0),且是狹長型負相關。可知兩個係數的相關性都非常地顯著。
迴歸結果物件FH_1vlm內,據有很多其他資訊,不是直接用summary()就可以全叫出來。這是因為R是用串列list()的原理在處理資訊。要進一步去看,可以用names()函數於兩個物件:
names(FH_1vlm) 和names(summary(FH_1vlm))
names(FH_1vlm) 可以看到 FH_1vlm內的物件
## [1] "coefficients" "residuals" "effects" "rank"
## [5] "fitted.values" "assign" "qr" "df.residual"
## [9] "xlevels" "call" "terms" "model"names(summary(FH_1vlm)) 可以看到 summary(FH_1vlm)內的物件:
## [1] "call" "terms" "residuals" "coefficients"
## [5] "aliased" "sigma" "df" "r.squared"
## [9] "adj.r.squared" "fstatistic" "cov.unscaled"
用符號 $ 擷取資訊。這兩個物件的子物件,有一些名稱重複;但是,內容是不同的。例如,係數(coeffieicnts),兩者皆有,但是,summary(FH_1vlm)$coef只有估計值,names(summary(FH_1vlm))$coef較為詳細。如下:
## (Intercept) SAVING
## 17.3286436 0.3233299## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 17.3286436 1.19014654 14.560092 1.293509e-28
## SAVING 0.3233299 0.05439557 5.944049 2.627034e-08用R進行實證分析,必須要將結果到文字編輯軟體。因為LaTex的說明,對於使用Tex的人,應該都可以知道。目前,我們假設讀者使用的是微軟的WORD,如果是這樣,可以將係數表格,存入csv格式,再於WORD內插入物件即可。
myTable01=summary(FH_1vlm)$coef
write.csv(myTable01, file= "myTable01.csv")
當我們在R執行完線性迴歸lm()後,且也將迴歸結果存成物件,例如上例存成FH_1vlm,R對這個物件的迴歸後統計分析相當多,我們稱之為
R 底層(Base R )函數,如下表所列。
## BaseR description
## 1 print 將資訊列印於螢幕
## 2 summary 資訊摘要
## 3 coef 係數資訊
## 4 residuals 迴歸殘差
## 5 fitted 迴歸配適值資訊
## 6 anova 變異數分析
## 7 predict 迴歸推測
## 8 plot 繪圖
## 9 confint 迴歸係數之信任區間
## 10 deviance 計算模型的SSE
## 11 vcov 共變異數矩陣)
## 12 logLik 對數概似值
## 13 AIC AIC值
## 14 BIC BIC值
接下來,就是對上表函數使用的介紹。
這裡我們使用了函數with()和 with(plot(SAVING, INVEST), data=myData)
因為plot()不像lm(…, data=)裡面可以宣告資料集,如果單獨使用,就必須這樣
plot(myData$SAVING, myData$INVEST) 或
attach(myData)
plot(SAVING, INVEST)
上述attach()的做法,要小心一點。如果整個工作空間只有一個檔案,變數就不會有重複的名稱,那就可以一開始就用attach()宣告資料,這樣,像lm()的函數,都不用在argument內宣告資料集。
使用with()或宣告函數內資料集,而不使用全域attach()函數。因為,當手上有許多跨國資料時,很多變數的名稱,因為慣用或通用,所以多是一樣的,例如,GDP。這樣的話會attach()多個檔案,會造成覆蓋。讀者還可以選擇自己習慣的作法。接下來我們再來診斷殘差。
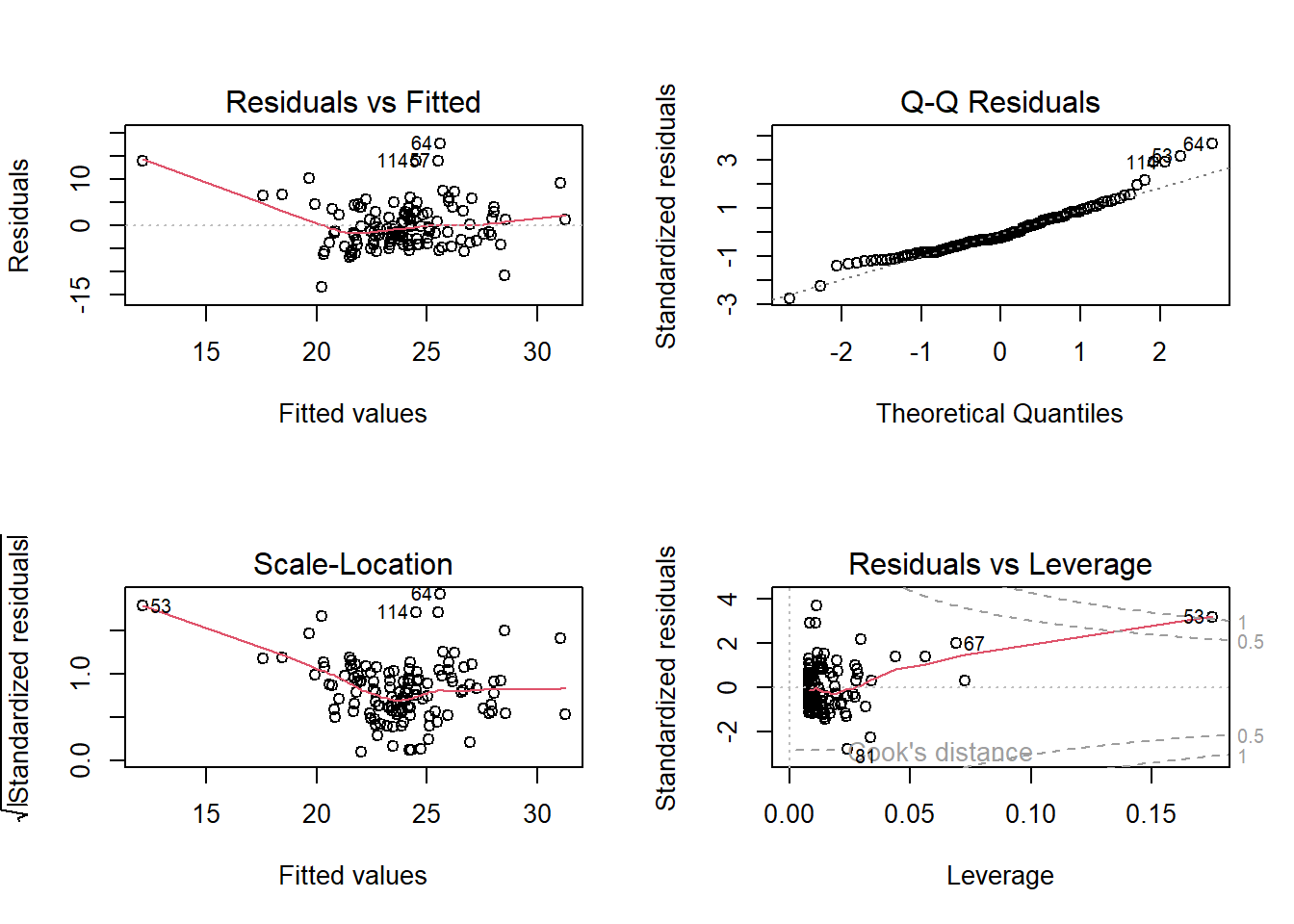
圖 1.3: 診斷殘差
par(mfrow=c(2,2)) 是將圖框分割成 \(2 \times 2\) 四格的視窗,
par(mfrow=c(1,1)) 則是將圖形框還原成 \(1 \times 1\) 單格視窗,
以免影響到後面的圖框結構。
par()是parameter的簡稱,有許多arguments,詳細內容可以在主控台鍵入?par查詢細節。
R對lm()函數的物件,繪製的殘差診斷圖有6個,內建為圖1.3的4個。
迴歸後的殘差診斷圖,會標出離群值的編號。圖1.3右下角的診斷圖中, 有一項Cook’s
distance,它計算了每一個樣本點的資訊,圖內的標號是依照Cook’s distance 判斷出來的離群值(outliers)。如果原始資料的列名稱有字串,好比人名或地名,則這裡會直接顯示文字。
再來檢視迴歸產生的條件期望值,或預期值、配適值,與對應的信賴區間。
FH_pred=predict(FH_1vlm, interval="confidence")
with(plot(INVEST~SAVING),data=myData)
abline(FH_1vlm) #繪製條件期望值或配適線
with(lines(FH_pred[,2] ~ SAVING, lwd=0.1, lty=4, col=2), data=myData)
with(lines(FH_pred[,3] ~ SAVING, lwd=0.1, lty=4, col=2), data=myData)
legend("topleft", c("配適線", "下界", "上界"), lty=c(1,4,4), lwd=0.1, bty="n")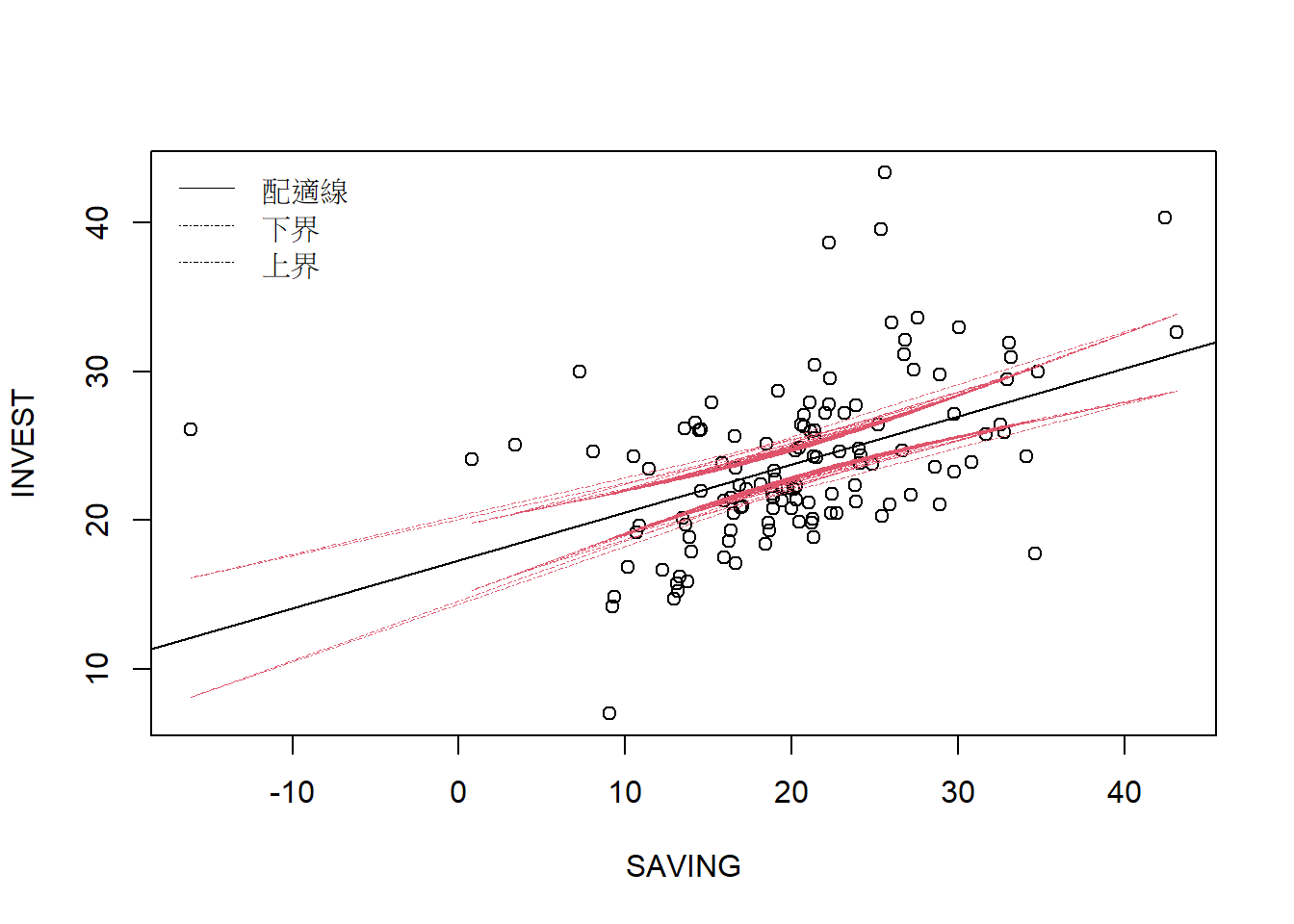
上圖我們使用abline(FH_1vlm)繪製條件期望值或配適線函數,用predict()計算期望值,並透過interval="confidence"參數計算信任區間。
估計完畢,接下來是檢定參數的特定關係。好比,如果某理論認為儲蓄對投資的影響是20%,則我們可以從事如下程式的檢定:
## Linear hypothesis test
##
## Hypothesis:
## SAVING = 0.2
##
## Model 1: restricted model
## Model 2: INVEST ~ SAVING
##
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 125 3045.6
## 2 124 2924.4 1 121.23 5.1406 0.0251 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1上述檢定其實就是ANOVA的觀念。看P-值,Pr(>F) =0.0251,可以知道: 在0.05
的顯著水準, F檢定拒絕了係數為0.2的虛無假設。
1.2 連續變數線性複迴歸
1.2.1 相異兩個解釋變數
\[
INVEST=a+b_{1} \times SAVING + b_{2} \times CA +e
\]
執行迴歸
結果摘要
##
## Call:
## lm(formula = INVEST ~ SAVING + CA, data = myData)
##
## Residuals:
## Min 1Q Median 3Q Max
## -12.4468 -1.5072 -0.2913 0.8785 22.0373
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.90313 1.28496 5.372 3.74e-07 ***
## SAVING 0.73175 0.05420 13.500 < 2e-16 ***
## CA -0.68305 0.06291 -10.858 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.484 on 123 degrees of freedom
## Multiple R-squared: 0.6026, Adjusted R-squared: 0.5962
## F-statistic: 93.26 on 2 and 123 DF, p-value: < 2.2e-16ANOVA檢定單變數和雙變數誰好
## Analysis of Variance Table
##
## Model 1: INVEST ~ SAVING
## Model 2: INVEST ~ SAVING + CA
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 124 2924.4
## 2 123 1493.2 1 1431.2 117.89 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1檢定線性假設: \(b_1+b_2=0\)
## Linear hypothesis test
##
## Hypothesis:
## SAVING + CA = 0
##
## Model 1: restricted model
## Model 2: INVEST ~ SAVING + CA
##
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 124 1506.5
## 2 123 1493.2 1 13.308 1.0962 0.29721.2.2 解釋變數的冪次方
\[
INVEST=a+b_{1} \times SAVING + b_{2} \times SAVING^{2} +e
\]
corr=TRUE計算估計係數的相關性
在lm()內,要處理同樣一個解釋變數的平方,好比多項式迴歸的作法,直接平方是不行的,例如,lm(INVEST~SAVING+SAVING^2)
是不行的。必須用隔離函數I()才能發揮作用 。上式的結果如下,
##
## Call:
## lm(formula = INVEST ~ SAVING + I(SAVING^2), data = myData)
##
## Residuals:
## Min 1Q Median 3Q Max
## -13.5391 -3.3607 -0.6522 2.8521 17.9544
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 20.237217 1.418935 14.262 < 2e-16 ***
## SAVING -0.060552 0.122925 -0.493 0.623178
## I(SAVING^2) 0.010269 0.002978 3.449 0.000772 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.656 on 123 degrees of freedom
## Multiple R-squared: 0.2904, Adjusted R-squared: 0.2788
## F-statistic: 25.16 on 2 and 123 DF, p-value: 6.896e-10
##
## Correlation of Coefficients:
## (Intercept) SAVING
## SAVING -0.86
## I(SAVING^2) 0.59 -0.91
我們看最後面故係數的相關係數,SAVING和SAVING^2兩個解釋變數係數的相關係數高達
-0.9:這意味著一個係數大,另一個就會小。為了處理這樣的問題,我們可以用正交多項式迴歸
orthogonal polynomial regression,
函數poly()可以取代解釋變數的輸入。讀者可以練習執行
summary(lm(INVEST~poly(SAVING,2),data=myData),corr =TRUE)
比較看一看,和上述結果差異有多大。
1.3 因子和交互效果
1.3.1 因子迴歸
因子變數是說這筆資料不是連續變數,而是虛擬變數。如果原始資料就是字串,那R會自動辨認其為因子。如果是數值,則需要宣告因子轉換factor()。如下例,
\[
INVEST=a+b_{1} \times SAVING + b_{2} \times CA +b_{3} \times Group + e
\]
變數Group是的文字,我們執行迴歸
結果摘要
##
## Call:
## lm(formula = INVEST ~ SAVING + Group, data = myData)
##
## Residuals:
## Min 1Q Median 3Q Max
## -13.1989 -2.9183 -0.5072 2.8354 17.0393
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 14.8400 1.5438 9.613 < 2e-16
## SAVING 0.3712 0.0569 6.524 1.75e-09
## GroupCentral and Eastern Europe 2.9960 1.6264 1.842 0.06794
## GroupCommonwealth of Independent States 5.0033 1.6181 3.092 0.00248
## GroupDeveloping Asia 1.9885 1.3841 1.437 0.15342
## GroupLatin America and the Caribbean 1.7428 1.2219 1.426 0.15640
## GroupMiddle East and North Africa 0.1560 1.3604 0.115 0.90892
##
## (Intercept) ***
## SAVING ***
## GroupCentral and Eastern Europe .
## GroupCommonwealth of Independent States **
## GroupDeveloping Asia
## GroupLatin America and the Caribbean
## GroupMiddle East and North Africa
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.722 on 119 degrees of freedom
## Multiple R-squared: 0.2938, Adjusted R-squared: 0.2581
## F-statistic: 8.249 on 6 and 119 DF, p-value: 1.79e-07
ANOVA 檢定:\(b_1=0\)
## Linear hypothesis test
##
## Hypothesis:
## SAVING = 0
##
## Model 1: restricted model
## Model 2: INVEST ~ SAVING + Group
##
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 120 3603.0
## 2 119 2653.8 1 949.16 42.562 1.747e-09 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
WALD 檢定:\(b_{1}=0\)
## Wald test
##
## Model 1: INVEST ~ SAVING + Group
## Model 2: INVEST ~ Group
## Res.Df Df F Pr(>F)
## 1 119
## 2 120 -1 42.562 1.747e-09 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 11.3.2 交互效果(Interaction terms)
交互效果是最簡單的線性模式擴充,也是一個描述係數非常數的最簡單方法。如下
\[
INVEST=a+b_{1} \times SAVING + b_{2} \times Group + b_{3} \times (SAVING \times Group) + e
\]
上式之中,原本是由下式出發
\[
INVEST=a+b_{1} \times SAVING + e
\]
但是,當研究者考慮係數\(b_{1}\)是否會與其他變數的高低有關,例如,Group有所不同時,則隱含了這樣的另一條方程式
\[
b_{1} = c + d \times Group
\]
這樣的方程式因為\(b_{1}\)不是資料,所以是無法估計的,因此必須帶入原式
\[
\begin{aligned}
INVEST &=a + ( c+ d \times Group) \times SAVING \\
&= a + c \times SAVING + d \times (SAVING \times Group)
\end{aligned}
\]
剩下都是符號問題。這就是interaction term的由來。
這樣才能解釋所估計出來的係數。我們的例子中,Group是文字變數,
所以是群組的意義。Interaction項,通常是由兩個連續變數所構成,如前例的平方項。有興趣的讀者,可以將前面的平方項,用一樣的方式,簡單推導一番。
##
## Call:
## lm(formula = INVEST ~ SAVING + Group + Group * SAVING, data = myData)
##
## Residuals:
## Min 1Q Median 3Q Max
## -8.8987 -2.7839 -0.8556 2.8868 15.4483
##
## Coefficients:
## Estimate Std. Error t value
## (Intercept) 13.9827 3.0406 4.599
## SAVING 0.4086 0.1281 3.190
## GroupCentral and Eastern Europe 6.3508 4.8035 1.322
## GroupCommonwealth of Independent States 9.6650 3.7991 2.544
## GroupDeveloping Asia -8.4189 4.2872 -1.964
## GroupLatin America and the Caribbean 4.0163 3.9238 1.024
## GroupMiddle East and North Africa 3.5312 4.3658 0.809
## SAVING:GroupCentral and Eastern Europe -0.1833 0.2410 -0.761
## SAVING:GroupCommonwealth of Independent States -0.2503 0.1660 -1.508
## SAVING:GroupDeveloping Asia 0.4648 0.1800 2.582
## SAVING:GroupLatin America and the Caribbean -0.1213 0.1894 -0.640
## SAVING:GroupMiddle East and North Africa -0.1443 0.1796 -0.803
## Pr(>|t|)
## (Intercept) 1.11e-05 ***
## SAVING 0.00184 **
## GroupCentral and Eastern Europe 0.18878
## GroupCommonwealth of Independent States 0.01230 *
## GroupDeveloping Asia 0.05200 .
## GroupLatin America and the Caribbean 0.30820
## GroupMiddle East and North Africa 0.42030
## SAVING:GroupCentral and Eastern Europe 0.44843
## SAVING:GroupCommonwealth of Independent States 0.13437
## SAVING:GroupDeveloping Asia 0.01108 *
## SAVING:GroupLatin America and the Caribbean 0.52320
## SAVING:GroupMiddle East and North Africa 0.42339
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.425 on 114 degrees of freedom
## Multiple R-squared: 0.4059, Adjusted R-squared: 0.3486
## F-statistic: 7.081 on 11 and 114 DF, p-value: 4.707e-09互動項的其他輸入方式如下:
lm(INVEST ~ SAVING + Group + Group:SAVING, data=myData)
lm(INVEST ~ SAVING + Group + Group/ SAVING, data=myData)
lm(INVEST ~ (Group + SAVING)^2, data=myData)
第3種作法,在多個變數的交叉互動下,相當好用。唯一會受影響的是估計結果的參數排序,R會自動處理重複問題,相當方便。
1.4 迴歸診斷
1.4.1 異質殘差檢定
古典迴歸假設迴歸殘差是同質變異(homoskedasticity),一個同質變異的迴歸,概念上是這樣:假設一條觀察值為1,000的迴歸:
\(Y=a+bX+e\),\(e\)是估計誤差項。變異數是殘差的平方和,同質變異就是var(e)=\(\sigma^{2}\)。有時更廣義的寫法,是用分配表示:\(e \sim N(0,\sigma^{2})\)。
所謂的同質變異,直觀的說法可以這樣表示:從1,000個e的資料集,隨機抽取若干觀察值,例如,50、150、300個,三個樣本變異數在統計上皆無差異。反之,異質變異就是說,依此計算的三個變異數,統計上不相等。
異質變異的問題,如果在時間序列資料,可以用某時間前後區分出兩個不同的變異數,計量學者稱之為結構變動(structural
breaks),著名的 Chow 檢定和其他結構變動檢定,
多是基於這樣的思路。如果資料沒有考慮殘差異質變異的性質,LS的估計往往會過度顯著。因此,檢定殘差是否具有異質性就相當重要。文獻上對於異質殘差的檢定有許多,時間序列資料的稱為ARCH,我們就不在這裡談。我們簡介兩種: Breusch and Pagan (1979) 和 Goldfeld and Quandt (1973) 。
Goldfeld-Quandt檢定,先估計一k個變數之迴歸式:
\[
Y_{i}=a+bX_{i}+e_{i}
\]
Goldfeld-Quandt
檢定的虛無假設為資料是同質變異。要檢定此虛無假設,假設變異數\(\sigma^{2}\)
和資料\(X_{i}\) 關系如下:
\[
\sigma_{i}^{2} = \sigma^{2}X_{i}^{2}
\]
\(\sigma^{2}\) 為常數。若上式為真,則當\(X\) 的值越大,\(\sigma_{i}^{2}\) 越大;
故 \(\sigma_{i}^{2}\) 不再是常數。Goldfeld-Quandt設計如下檢定程序:
Step 1.將原始資料 X 由小排到大。
Step 2.將中間c個樣本移除,留下雙端兩群資料,這兩群樣本數皆相等。
Step 3.對這兩群資料配適原LS迴歸。 - Step 4.令第1群的殘差平方和為RSS1,自由度=
\({\frac {n-c}{2}}-k\) ;第2群為RSS2,自由度= \({\frac{n-c}{2}}-k\)
。依此,Goldfeld-Quandt 計算如下
\[
\lambda = \frac{\frac{RSS_{2}}{df}}{\frac{RSS_{1}}{df}}=\frac{RSS_{2}}{RSS_{1}}
\]
df為自由度(degree of freedom)。如果虛無假設是正確的,這兩群資料的迴歸變異數會幾乎相等。在常態分配假設下, \(\lambda\)會是\(F\) 分配。Goldfeld-Quandt檢定需要挑一個解釋變數來排序,因此,挑哪一個來排序的結果就很關鍵。
Breusch-Pagan的檢定,則對所有的解釋變數蒐集資訊。假設某三變數迴歸:
Step 1.
\[
Y_{i}=a+b_{1}X_{1i}+b_{2}X_{2i}+b_{3}X_{3i}+e_{i}
\]
Step 2.
\[
e_{i}=c+d_{1}X_{1i}+d_{2}X_{2i}+d_{3}X_{3i}+ \varepsilon_{i}
\]
Step 3.檢定同質變異
\[
H_{0}:d_{1}=d_{2}=d_{3}=0
\]
Step 3的檢定量為 \(\frac{1}{2}ESS \sim \chi_{k-1}^2\) 。\(k\) 是Step2解釋變數的個數,\(ESS\) 是Step 2迴歸殘差的平方和。
執行Goldfeld-Quandt test,以SAVING排序如下。
##
## Goldfeld-Quandt test
##
## data: FH_2vlm
## GQ = 0.64452, df1 = 60, df2 = 60, p-value = 0.9542
## alternative hypothesis: variance increases from segment 1 to 2
執行Breusch-Pagan test
##
## studentized Breusch-Pagan test
##
## data: FH_2vlm
## BP = 21.523, df = 2, p-value = 2.12e-05虛無假設之下是同質變異,兩個檢定的差異很大,須要進一步研究方能確認,這種情況也是計量實證研究時常遇到的事。
1.4.2 迴歸函數形式判定
迴歸方程式如果函數形式設定錯誤,如何判定?文獻上有許多檢定方法如 。Ramsey (1969)
的RESET檢定是較早提出來的一種。假設某雙變數迴歸:
Step 1. 執行迴歸
\[
Y_{i}=a+b_{1}X_{1i}+b_{2}X_{2i}+e_{i}
\]
令配適值為\(\hat Y_{i}\) ,自由度為\(DF_{A}\) ,且相關係數為\(R_{A}^2\)。
Step 2. 新增變數\(k\)個,再執行迴歸,以\(k=2\)為例:
\[
Y_{i}=a+b_{1}X_{1i}+b_{2}X_{2i}+b_{3}\hat Y_{i}^2+b_{4}\hat Y_{i}^3+e_{i}
\]
上式相關係數為\(R_{B}^2\)
Step 3. 計算\(F\) 檢定量
\[
F=\frac{R_{B}^2-R_{A}^2}{1-R_{A}^2} \frac{DF_{A}}{k}
\]
這個檢定一般稱為RESET。如果 \(F\) 值大於特定顯著水準, e.g. 5%,
的臨界值,則拒絕了模型函數設定是完整的虛無假設。使用這個統計量時,必須對被解釋變數和殘差的關係,做一些檢視。如果有曲度性(curvilinear)關係,則可以RESET檢定配適關係。
Utts (1982) 則和RESET與的類似,且使用了Goldfeld-Quandt的排序方法來做非線性區度檢定。 Harvey and Collier (1977) 提出的統計量是檢定Recursive residuals, 一般視為CUSUM的延伸:漸進上,如果模型的函數設定是正確的,則Recursive
residuals的平均數為0。這些檢定的技術層次,我們就不細說,直接看R如何執行就可以。
RESET 檢定如下:
##
## RESET test
##
## data: FH_2vlm
## RESET = 49.604, df1 = 2, df2 = 121, p-value < 2.2e-16
Rainbow test 檢定如下:
##
## Rainbow test
##
## data: FH_2vlm
## Rain = 12.215, df1 = 63, df2 = 60, p-value < 2.2e-16
Harvey test 檢定如下:
##
## Harvey-Collier test
##
## data: FH_2vlm
## HC = 0.25771, df = 122, p-value = 0.7971
套件lmtest有一些基本的檢定量,如果需要更多診斷,讀者可以參考套件fRegression內所附帶的迴歸後檢定。
1.4.3 穩健共變異數的異質變異修正 Robust Covariance for heteroskedasticity
我們介紹當殘差出現異質變異,則需要修正這種異質性,再重新計算的共變異數,稱為穩健共變異數(Robust Covariance)。這裡有兩個問題須要釐清處:
(1)此處所稱的穩健共變異數,和文獻上處理離群值(outliers)的Robust Regression不同。 例如,分量迴歸,L-和M-估計法等等。這些估計方法,會重新估計LS模型的方程式,全體參數都會重新計算。
(2) 處理異質變異的Robust Covariance只會修正標準差,不會改變原先LS估計的參數。 如果原來OLS的係數檢定很顯著,一般而言,修正異質變異的穩健標準差,會讓原先的檢定結果更穩健,更保守,也就是降低顯著性;例如,p-value從0.002變成0.04。
LS假設殘差為同質,模型的共變異數的估計式為下式
\[
\begin{equation}
\tag{1.6}
E[\varepsilon_{i}^2] =
\begin{pmatrix}
\sigma^{2} & 0 & \cdots & 0 \\
0 & \sigma^{2} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & \sigma^{2}
\end{pmatrix}
=\sigma^{2} \mathrm{I_n}
\end{equation}
\]
假設異質變異為\(E[\varepsilon_{i}^2] =\sigma^2x_{i}^2\)
,則共變異數矩陣為:
\[
\tag{1.7}
cov(b)=(X'X)^{-1}X' \Omega X(X'X)^{-1}
\]
\[
\begin{equation}
\tag{1.8}
E[\varepsilon_{i}^2]=\sigma^{2}
\begin{pmatrix}
x_{1}^{2} & 0 & \cdots & 0 \\
0 & x_{2}^{2} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & x_{n}^{2}
\end{pmatrix}
=\Omega
\end{equation}
\]
也就是說
\[
y=Xb+\varepsilon, \;\; E[\varepsilon]=0, \; \; E[\varepsilon \varepsilon']=\Omega
\]
此時,\(E[b]=\beta\) 依然是不偏的,但是
\[
\tag{1.9}
var(b)=(X'X)^{-1}X' \Omega X(X'X)^{-1}
\]
當殘差有異質變異時,LS估計的變異數就不再不偏,一般的情況會過度膨脹t統計量,而使的所估計的係數都很顯著。如果殘差異值變異的特徵,有某種類型或規律,例如,分群分組就可以辨認出來,則我們可以由群組的方向去修正。有時後分組變數是產業,則控制產業的集群(cluster),就可以降低影響;有時後是時間點,如前述之結構變動,分期之後,就可以解決。
像這樣的問題,在於如果殘差是異質的,但是我們將所有殘差視為同質,則計算期望值時,每個樣本點的權重都一樣,所以會導致變異數低估,顯著性會高估。當然,某些特殊情況會例外。
令方陣\(\Omega\)
第i個主對角元素為\(\omega_i\),\(R\)模組異質性修正有五種:
\[ constant: \omega_{i}=\hat \sigma^2 \\ HC_0: \omega_{i}=\hat \varepsilon_{i}^2 \\ HC_1: \omega_{i}=\frac{n}{n-k}\hat \varepsilon_{i}^2 \\ HC_2: \omega_{i}=\frac{\hat \varepsilon_{i}^2}{1-h_{ii}} \\ HC_3: \omega_{i}=\frac{\hat \varepsilon_{i}^2}{(1-h_{ii})^2} \\ HC_4: \omega_{i}=\frac{\hat \varepsilon_{i}^2}{(1-h_{ii})^{\delta_i}} \\ \]
\(k\) 是解釋變數個數,\(h_{ii}\) 是 \(H=X(X'X)^{-1}X'\) 矩陣第\(i\) 個主對角元素,\(\bar h\) 為其平均數,$_{i}=min(4, )$。
HC0是指 White (1980) 的方法,HC1~HC3則是近來被建議提升小樣本表現的共變異數矩陣。HC4則對具影響力的觀察值(influential observations)給予特別權重。對於考慮殘差異質性和序列相關的頑強共變異數,R的package是sandwich。穩健共變異數的考慮,不會改變所估係數的值,只會修正共變異數,也就是標準差。R做穩健共變數估計選項,非常簡易,只需要將lm()的迴歸物件用vcovHC處理即可重新計算共變異數矩陣。請看以下程式碼:
vcovHC()的一般形式,有很多選項。這部份我們留到後面panel data時再詳述。 我們將有修正與無修正的結果並列比較,如下:
無修正之估計結果如下,使用lmtest內的coeftest()
##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.903126 1.284961 5.3722 3.742e-07 ***
## SAVING 0.731745 0.054204 13.4999 < 2.2e-16 ***
## CA -0.683053 0.062910 -10.8576 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1vcovHC 計算穩健共變異數,修正方法內定HC0。
##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.90313 4.77736 1.4450 0.1510101
## SAVING 0.73175 0.20346 3.5965 0.0004654 ***
## CA -0.68305 0.15535 -4.3968 2.349e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
修正方法選用HC1。
##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.90313 3.84265 1.7965 0.07488 .
## SAVING 0.73175 0.16345 4.4769 1.705e-05 ***
## CA -0.68305 0.13132 -5.2016 7.998e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1比較發現,考慮穩健共變異數後的標準差會比較大,使的顯著性檢定的結果趨於保守,不會太輕易就拒絕虛無假設,也使的迴歸結果較為可靠。
1.5 時間序列迴歸
如果我們要執行時間序列資料的線性迴歸,例如 \(Y_{t}=a+b_{0}X_{t}+e\) , 如果殘差沒有序列相關修正問題時,這個迴歸基本上可以用lm()處理。但是,如果我們的迴歸方程式有落後期,如\(Y_{t}=a+b_{0}X_{t}+b_{1}X_{t-1}+b_{2}X_{t-2}+e\) ,則lm()就會有一些麻煩,因為落後的資料會出現缺值,所以,必須另外處理。我們看下面程式例子:台灣經濟成長率和自己的落後期迴歸。
## Saving Investment Growth
## 1 0.086739 0.097278 0.0812
## 2 0.114177 0.118885 0.0808
## 3 0.097690 0.109438 0.1142
## 4 0.151308 0.123959 0.0520
## 5 0.129564 0.107371 0.1343
## 6 0.141047 0.131242 0.0984## Saving Investment Growth
## [1,] 0.086739 0.097278 0.0812
## [2,] 0.114177 0.118885 0.0808
## [3,] 0.097690 0.109438 0.1142
## [4,] 0.151308 0.123959 0.0520
## [5,] 0.129564 0.107371 0.1343
## [6,] 0.141047 0.131242 0.0984
使用套件dynlm可以保留時間序列的刻度。看下面例子
library(dynlm)
dynlm_twn=dynlm(Growth ~ L(Saving) + L(Saving, 4),data=myTS_Dates)
summary(dynlm_twn)##
## Time series regression with "ts" data:
## Start = 1963(1), End = 2010(4)
##
## Call:
## dynlm(formula = Growth ~ L(Saving) + L(Saving, 4), data = myTS_Dates)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.157737 -0.016404 0.002062 0.023373 0.093613
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.12802 0.01277 10.027 < 2e-16 ***
## L(Saving) 0.07551 0.06988 1.080 0.281
## L(Saving, 4) -0.28113 0.06627 -4.242 3.46e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.03909 on 189 degrees of freedom
## Multiple R-squared: 0.1366, Adjusted R-squared: 0.1274
## F-statistic: 14.95 on 2 and 189 DF, p-value: 9.401e-07
我們再看殘差如下圖,時間刻度保持的很好,直接以時間序列的繪圖方式將散佈點接起來。
dynlm()是一個很好用的時間序列迴歸函數。讀者可以用lm()做做看,在lm()內,很多時間序列功能都無法使用。
1.6 線性重合檢定
在複迴歸模型,因為解釋變數有多個,所以解釋變數之間如果彼此有強烈線性相關時,我們稱為共線性(collinear)問題。當線性重合存在時,解釋變數之間的正交性質就會受到影響,最極端的行情況就是產生奇異問題(singularity),此時,估計出來的係數不穩定,也非唯一。檢查共線性的方法有以下多種:
1. 計算解釋變數之間成對的相關係數矩陣。
2.將解釋變數之間互相迴歸。如果有很高的R2,則線性重和就存在。
3. 令\(X\) 代表解釋變數矩陣,計算矩陣XTX的特徵值(eigenvalues),將特徵值從大到小排序後,特徵值相對偏小的變數會有線性重合問題。假設最大特徵值為\(\lambda_{1}\) ,最小特徵值為\(\lambda_{p}\) ,統計學者建構了一個指數condition number 如下:
\[ condition \; number=\sqrt{ \frac{\lambda_{1}}{\lambda_{p}}} \]
這個數字若大於30被視為是夠大,也就是矩陣出現singularity。
4.因為線性重合存在時,會導致所估計參數的變異數龐大,可由下式看出
\[ var(b_j)=\frac{1}{1-R_{j}^2} \frac{s^2}{(x_{jj}- \bar x_j)^2} \]
第j個自變數與其他自變數迴歸的偏相關係數接近1時,第1項分母會趨近0,所以此變異數會膨脹。因此,統計學者定義variance inflation factor(VIF)如下:
\[ VIF_j=\frac{1}{1-R_{j}^2} \]
VIF越大,代表線性重合的問題越嚴重。R計算VIF有套件DAAG和套件faraway,都稱為vif()。faraway必須先宣告model.matrix再剔除截距項,較為囉唆。本書建議使用DAAG內的較為簡便。
我們先執行三變數線性迴歸,並將迴歸後結果存為物件G。
##
## Call:
## lm(formula = wage ~ education + experience + age, data = CPS1985)
##
## Residuals:
## Min 1Q Median 3Q Max
## -8.351 -2.857 -0.599 1.994 36.336
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -4.76987 7.04271 -0.677 0.499
## education 0.94833 1.15524 0.821 0.412
## experience 0.12756 1.15571 0.110 0.912
## age -0.02241 1.15475 -0.019 0.985
##
## Residual standard error: 4.604 on 530 degrees of freedom
## Multiple R-squared: 0.202, Adjusted R-squared: 0.1975
## F-statistic: 44.73 on 3 and 530 DF, p-value: < 2.2e-16
由以上迴歸結果,發先三個變數都不顯著。但是,F-statistic很顯著,Multiple
R-squared 也有20%。這就很有可能是線性重合導致的現象。計算三個解釋變數的vif()值,如下:
## education experience age
## 229.57 5147.90 4611.40
VIF果然很大,畢竟這三個變數都跟時間有關。若VIF<10的解釋變數可以接受,所以在實務上,我們會逐次剔除VIF大於10的解釋變數。這三個解釋變數的VIF值都相當龐大,以education為例,解釋如下:
我們這樣解釋:教育變數目前的標準差為1.155,比無線性重合時高出15倍多。檢視其餘兩個,我們發現所有解釋變數之間都有極大的VIF,所以,這個線性迴歸的估計和檢定均不可靠。
克服線性重合的方法是依照理論剔除多餘的解釋變數,或利用ridge regression,R有lm.ridge()可以處理,或工具變數方法(Two-stage LS),此章我們就不詳述。
References
這個小數宣告,不是恰有4位小數點。R會以4位小數自動的判讀與對齊,所以,自動調整對齊和美觀的要求。↩︎