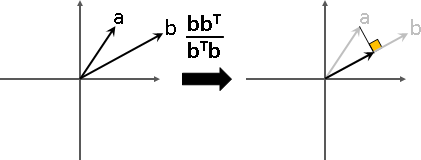eigenbasis - root finding
本章主角是特徵向量與特徵值(真實版本)
矩陣求根
本站文件「root finding」,介紹了「輸入、輸出只有一個變數」的函數,以及根、解、不動點、特徵點。
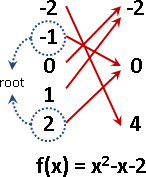
此處介紹「輸入、輸出有很多個變數」的線性函數,以及根、解、不動向量、特徵向量。
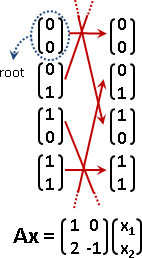
根(核):Ax = 0,符合條件的x。
線性函數必定有一個根:零向量x = 0,缺乏討論意義。
線性函數通常有許多個根,並且組成空間,空間維度等於A的座標軸數量減去A的rank。白話解釋:座標軸無法觸及之處,當然輸出0囉。另外rank、determinant可以判斷是否有許多個根。
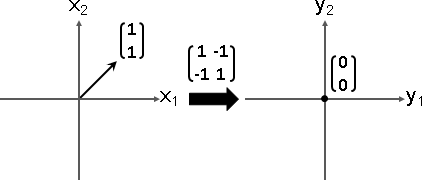
解:Ax = b,符合條件的x。b是已知的、特定的向量。
類似於根。請見本站文件「linear equation」。
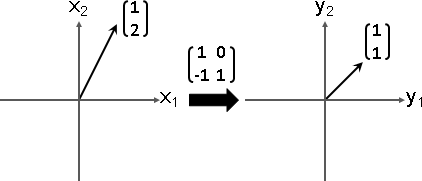
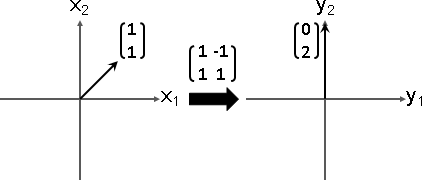
不動向量:Ax = x,符合條件的x。
線性函數必定有一個不動向量:零向量x = 0。
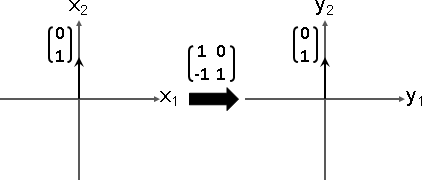
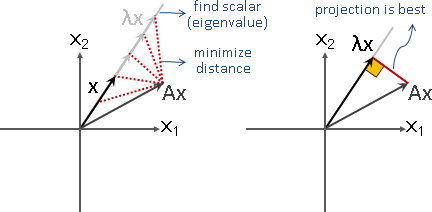
特徵向量:Ax = λx,符合條件的x。λ是任意一種倍率。
線性函數通常有許多個特徵向量,後續文章的主角。
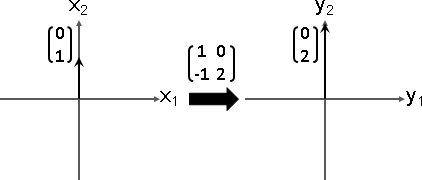
eigenvector / eigenvalue
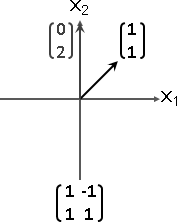
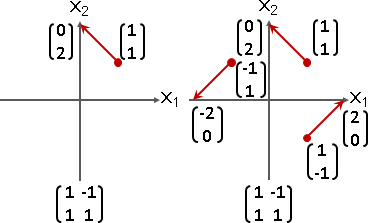
針對一個線性函數,從眾多的輸入向量當中,找到其中一些輸入向量,讓輸出向量恰是輸入向量乘上倍率,此時輸入向量稱作「特徵向量」,倍率稱作「特徵值」。
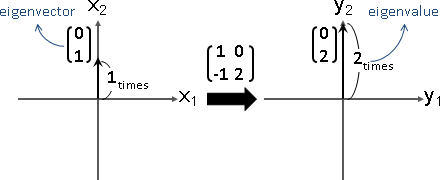
數學式子是Ax = λx。A是線性函數,x是輸入向量,λx是輸出向量。x是特徵向量,λ是特徵值。
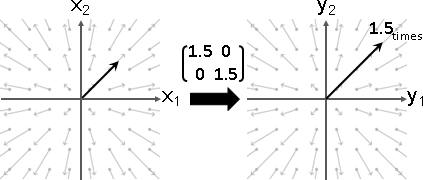
特徵向量變換之後,長度伸縮,方向相同或相反。
特徵值可正、可負、可零。正的伸縮,負的伸縮兼翻轉,零的長度歸零。
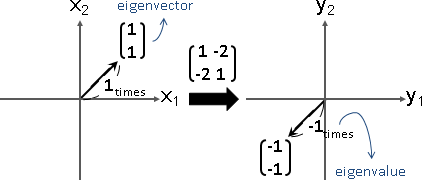
特徵向量有無限多個
零向量必定是特徵向量,缺乏討論意義,大家習慣無視它。
特徵向量的任何一種倍率(方向相同或相反),也是特徵向量,也是相同特徵值。大家習慣取長度為一的特徵向量當作代表,方向則隨意。
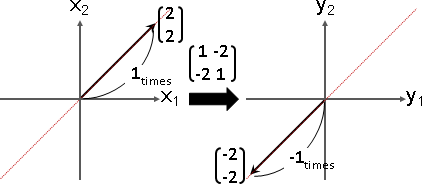
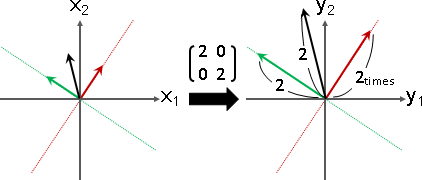
方向不同的特徵向量,如果恰好擁有相同特徵值,那麼這些特徵向量構成的平面、空間、……當中的任何一個向量,也是特徵向量,也是相同特徵值。大家習慣取互相垂直的特徵向量當作代表,方向則隨意。
characteristic equation / characteristic polynomial
無邊無際、無窮無盡,如何找到特徵向量和特徵值呢?
嘗試解Ax = λx。移項Ax - λx = 0。合併(A - λI)x = 0。
若是唯一解,那麼x顯然是零向量。缺乏討論意義。
若有其他解,那麼令det(A - λI) = 0,稱作「特徵方程式」。展開det(A - λI),形成λ的多項式,稱作「特徵多項式」。
先求特徵值λ:展開det(A - λI) = 0,特徵多項式求根。
再求特徵向量x:特徵值代入(A - λI)x = 0,線性函數求根。
一種特徵值,得到一種特徵向量。
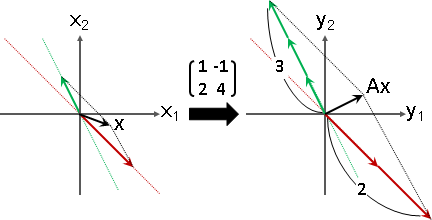
A = ⎡ 1 -1 ⎤ A - λI = ⎡ (1-λ) -1 ⎤ det(A - λI) = 0
⎣ 2 4 ⎦ ⎣ 2 (4-λ) ⎦ => (1-λ)(4-λ) + 2 = 0
=> λλ - 5λ + 6 = 0
=> λ = 2 or 3
when eigenvalue λ = 2 | when eigenvalue λ = 3
|
(A - λI) x = 0 | (A - λI) x = 0
|
⎡ (1-2) -1 ⎤ ⎡x₁⎤ = ⎡0⎤ | ⎡ (1-3) -1 ⎤ ⎡x₁⎤ = ⎡0⎤
⎣ 2 (4-2) ⎦ ⎣x₂⎦ ⎣0⎦ | ⎣ 2 (4-3) ⎦ ⎣x₂⎦ ⎣0⎦
|
get ⎰ x₁ = 1k | get ⎰ x₁ = 1k
⎱ x₂ = -1k | ⎱ x₂ = -2k
|
then eigenvector x = ⎡ 1⎤ | then eigenvector x = ⎡ 1⎤
⎣-1⎦ | ⎣-2⎦
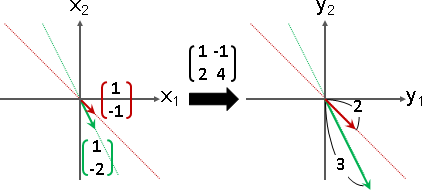
特徵向量最多N種
數學家藉由determinant與characteristic polynomial定義特徵值:N-1次多項式必有N個根,必得N個特徵值。N是方陣邊長。
這種定義方式,儘管湊出了N個特徵值,卻可能湊不出N種特徵向量。詳細分析如下:
一、相異特徵值,各自擁有相異特徵向量,構成相異維度。
二、相同特徵值(重根),不見得都有特徵向量,但至少一種。
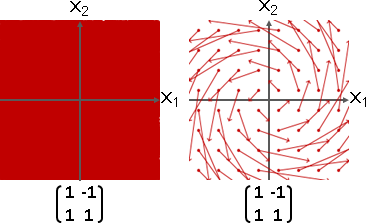
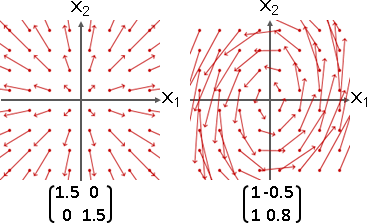
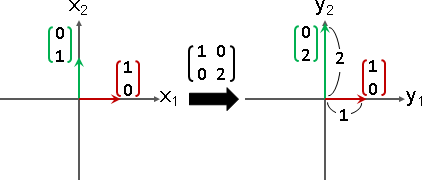
縮放矩陣:特徵值和特徵向量都是實數。特徵向量確實存在。
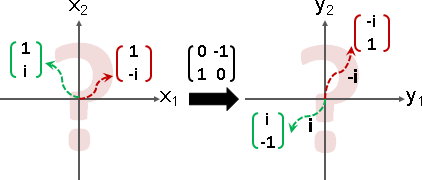
旋轉矩陣:特徵值和特徵向量都是複數。特徵向量確實存在,卻無法作圖。
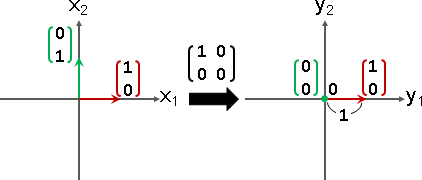
投影矩陣:特徵值有0。特徵向量確實存在。
歪斜矩陣:特徵向量不足N種。
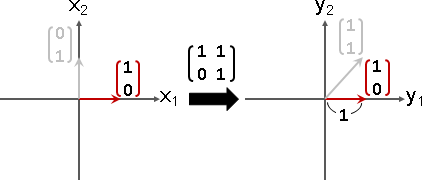
特徵向量演算法(characteristic polynomial)
一、多項式函數求根,取得特徵值。
二、線性函數求根(求解),取得特徵向量。
然而無法克服:一、根的範圍不明;二、根可能是複數。
沒人用這種方法計算特徵值、特徵向量。