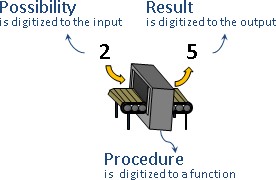
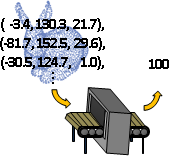
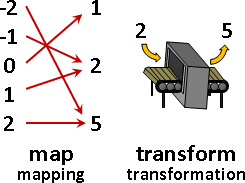
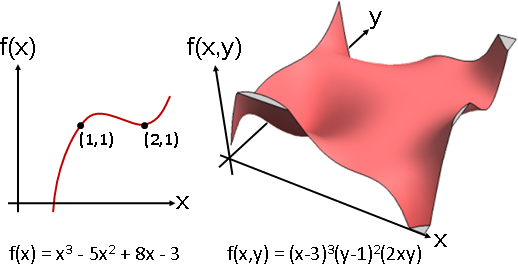
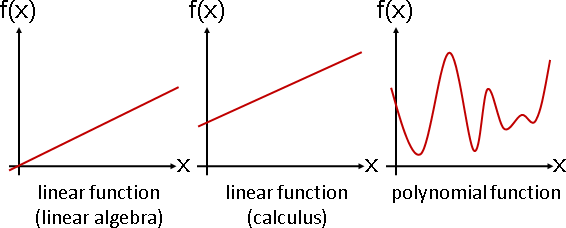
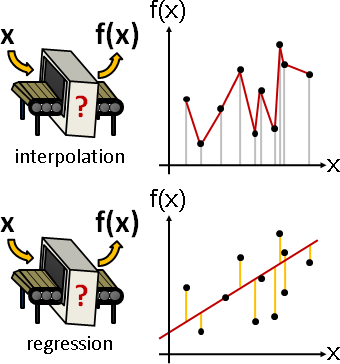
function運算(主角是函數)
■ logic
operation (noun) operation (verb) result (noun)
----- -------------------- ------------------ ------------------
( ) evaluation 求值 evaluate 求值 value 值
= substitution 代入 substitute 代入 expression 式
∘ composition 複合 compose 複合 composite function 複合函數
⁻¹ inversion 反演 inverse 反演 inverse function 反函數
■ arithmetic
----- -------------------- ------------------ ------------------
+ addition 加法 add 加 sum 和
- subtraction 減法 subtract 減 difference 差
⋅ multiplication 乘法 multiply 乘 product 積
/ division 除法 divide 除 quotient 商
■ calculus
----- -------------------- ------------------ ------------------
d/dx differentiation 微分 differentiate 微 derivative 導數
∫ dx integration 積分 integrate 積 integral 積分
■ analysis
----- -------------------- ------------------ ------------------
⟪ , ⟫ dot product 點積
∗ convolution 卷積
‖ ‖ norm 範數
■ comparison
----- -------------------- ------------------ ------------------
= equal than 等於 true/false 真/假
> greater than 大於 true/false 真/假
< less than 小於 true/false 真/假
■ optimization
----- -------------------- ------------------ ------------------
max maximization 最大化 maximize 最大化 maximum 最大值
min minimization 最小化 minimize 最小化 minimum 最小值
sup supremum 最小上界
inf infimum 最大下界
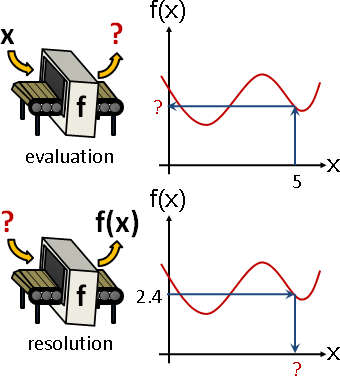
求值
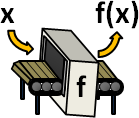
求值:給定輸入數值,計算輸出數值。
sin x cos y
f(x, y) = ————— + —————
y x
|
| x = 1
| y = 0.5
↓
sin 1 cos 0.5
f(1, 0.5) = ————— + ——————— = 2.56
0.5 1
代入
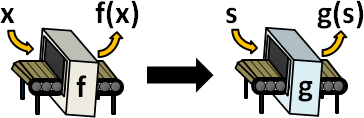
代入:輸入變數替換為其他變數,得到新函數。
sin x cos y
f(x, y) = ————— + —————
y x
|
| x = s+2
| y = t/2
↓
sin(s+2) cos(t/2)
g(s, t) = ———————— + ————————
t/2 s+2
複合
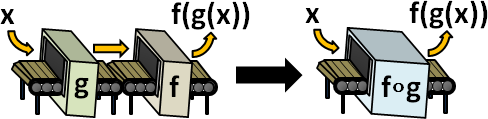
複合:如果經常接連求值,那麼可以預先把函數複合在一起,得到複合函數,節省計算時間!
兩個函數
f(x) = x² + x + 1
g(x) = -x + 2
輸入數值是1的時候,計算先通過g函數、再通過f函數的輸出數值
g(1) = -1 + 2 = 1
f(g(1)) = f(1) = 1² + 1 + 1 = 3
輸入數值是2的時候,計算先通過g函數、再通過f函數的輸出數值
g(2) = -2 + 2 = 0
f(g(2)) = f(0) = 0² + 0 + 1 = 1
如果預先讓函數複合
(f ∘ g)(x) = f(g(x))
= (-x + 2)² + (-x + 2) + 1
= x² - 5x + 7
那麼就可以節省計算時間
(f ∘ g)(1) = 1² - 5 + 7 = 3
(f ∘ g)(2) = 2² - 10 + 7 = 1
反演
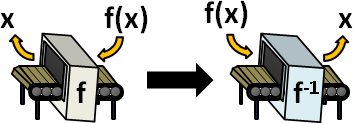
反演:如果經常求解,那麼可以預先把函數反演,得到反函數,節省計算時間!
一個函數
f(x) = log₂(x - 2)
輸出數值是1的時候,嘗試求得輸入x
f(x) = log₂(x - 2) = 1
x - 2 = pow₂(1)
x - 2 = 2¹
x - 2 = 2
x = 2 + 2
x = 4
如果預先讓函數反演
f⁻¹(x) = 2ˣ + 2
那麼就可以節省計算時間
f⁻¹(1) = 2¹ + 2 = 4
加減乘除
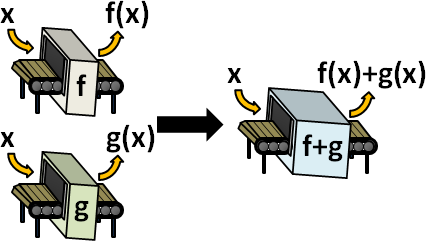
加減乘除:如果經常要把兩個函數的輸出加在一起,那麼可以預先把兩個函數加在一起,得到新函數,節省計算時間!
加減乘除概念相仿,其餘運算就不多提了。
兩個函數
f(x) = x² + x + 1
g(x) = -x + 2
輸入數值是1的時候,計算所有函數輸出數值的總和
f(1) = 1² + 1 + 1 = 3
g(1) = -1 + 2 = 1
f(1) + g(1) = 3 + 1 = 4
輸入數值是2的時候,計算所有函數輸出數值的總和
f(2) = 2² + 2 + 1 = 7
g(2) = -2 + 2 = 0
f(2) + g(2) = 7 + 0 = 7
如果預先讓函數相加
(f + g)(x) = f(x) + g(x)
= (x² + x + 1) + (-x + 2)
= x² + 3
那麼就可以節省計算時間
(f + g)(1) = 1² + 3 = 4
(f + g)(2) = 2² + 3 = 7
微分、積分
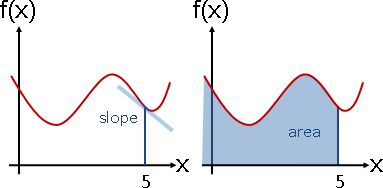
微分:輸出差距除以輸入差距。曲線的斜率。
積分:輸出加總乘以輸入差距。曲線下的面積。
點積、卷積
【不知道怎麼畫成圖片】
點積:兩個函數相乘、積分(負無限大到正無限大)。
卷積:很多次點積,其中一個函數左右翻面、一直平移。
範數
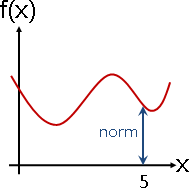
範數:輸出的大小。如果輸出變數有很多個,那麼範數有多種設定方式,例如向量長度(平方和開根號)(自點積開根號)。
等於、大於、小於
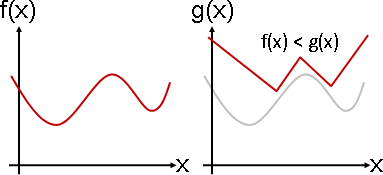
等於:兩個曲線,處處一樣高。
大於:第一個曲線,處處都較高。
小於:第一個曲線,處處都較低。
如果輸出變數有很多個,那麼可以用範數比大小。
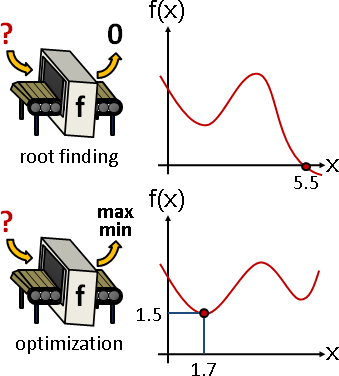
最大值、最小值
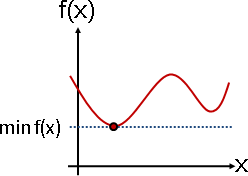
最大值:一個曲線的最高處。最大的輸出。
最小值:一個曲線的最低處。最小的輸出。
最小上界、最大下界
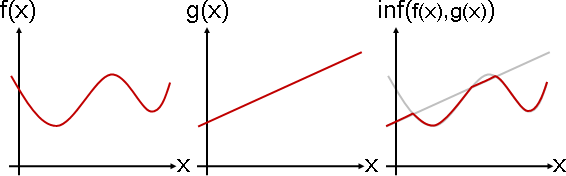
最小上界:多個曲線的最大值。
最大下界:多個曲線的最小值。
延伸閱讀:最小值min與最大下界inf
數學家給了嚴格定義。兩者都是「一群東西的最小者」,東西可以是整數、實數、函數、……,東西數量可以是有限、無限,東西範圍可以是有界、無界。兩者差別在於min
不含趨近,inf包含趨近。
範例:實數範圍大於零小於十(0,10),min不存在(永遠可以找到一個更接近0的實數),inf則是0。
範例:實數範圍從大於等於零小於等於十[0,10],min是0,inf也是0。
範例:https://math.stackexchange.com/questions/1106225/
計算學家有著另類用法。min是一群數值的最小數值,inf是一群函數的最大下界函數。min輸出數值,inf輸出函數。
範例:x* = minₓ f(x)是指一堆數字f(0)、f(1)、f(2)、……的最小數值。
範例:g(y) = infₓ f(x,y)是一堆一維函數f(0,y)、f(1,y)、f(2,y)、……的最大下界函數。
計算學只討論確切數字,於是這兩個範例的min和inf其實都是相等的。既然兩者互通,於是將min用在數值、inf用在函數,以增加資訊含量。