root

找到確切的輸入數值，讓輸出數值是零，稱作「求根」。這樣的輸入，稱作「根」，可能有許多個、也可能不存在。

以函數圖形表達函數的根：當輸入變數只有一個，是函數曲線與X軸的相交之處。當輸入變數只有兩個，是函數曲面與XY平面的相交之處。當輸入變數有許多個，請讀者自行推廣。

中學數學談過多項式函數的求根，相信大家印象深刻。比如一元二次多項式函數的求根（解一元二次多項式方程式），有個號稱數學界最難背的公式：二a分之負b正負根號b平方減四ac。

          _________
    -b ± V b² - 4ac
x = ———————————————
          2a

以下則是談一般的函數的求根。多項式函數，性質優美，擁有特定公式；一般的函數，雜亂無章，沒有固定公式，只好利用電腦了。最簡單的求根演算法，就是窮舉法：窮舉各種輸入，看看輸出是不是零。

// 使用了function pointer的語法。 // 把f(x)當作參數，比較有個函式的模樣了！ void roots(float (*f)(float)) { // 假設根可能在-100000到+100000之間 for (float x = -1e5; x <= +1e5; x += 0.001) // if (f(x) == 0) if (fabs(f(x)) < 0.001) // 避免誤差 cout << x << "是根"; }

窮舉法非常慢。接下來介紹更快的方法。

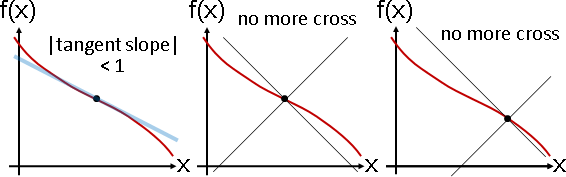
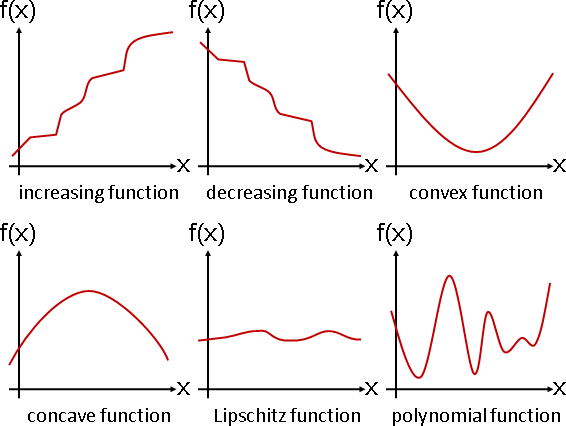
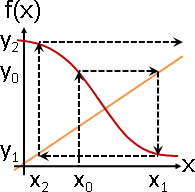用途

用來找到連續函數的根。bi-這個字首是「雙」的意思，而section是「分段」的意思。中文譯作「二分法」。

勘根定理

解釋演算法之前，得先複習一下高中數學的「勘根定理」。

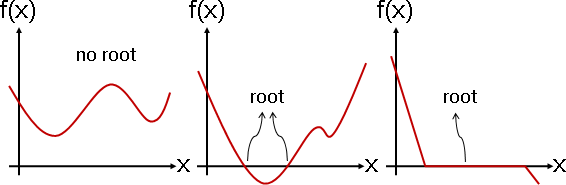
連續函數的圖形當中，當起點與終點分別在X軸的兩側，那麼一定在某處穿過X軸。換句話說，在某處有根。換句話說，至少有一個根。

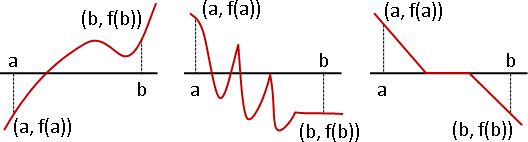
以數學符號說明勘根定理

連續函數f(x)，任意區間[a,b]。a和b分別代入f(x)，得到f(a)和f(b)。

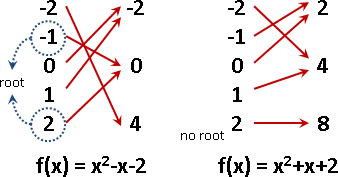
如果f(a)和f(b)是一正一負、是異號，即f(a) f(b) < 0，就表示座標(a, f(a))和座標(b, f(b))這兩點位於X軸的兩側。因為f是連續函數，所以座標(a, f(a))到座標(b, f(b))的路線，一定碰到X軸至少一次──區間[a,b]裡面至少有一個根。

如果f(a)和f(b)是同號，即f(a) f(b) > 0，就表示座標(a, f(a))和座標(b, f(b))這兩點位於X軸的同側──區間[a,b]裡面可能有根，也可能無根。

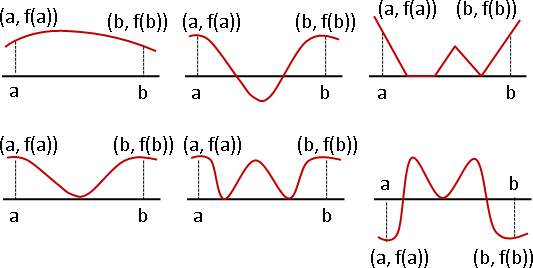
如果f(a)和f(b)有零，即f(a) f(b) = 0，此時a和b就是根──區間[a,b]裡面可能還有其他根，也可能無根。

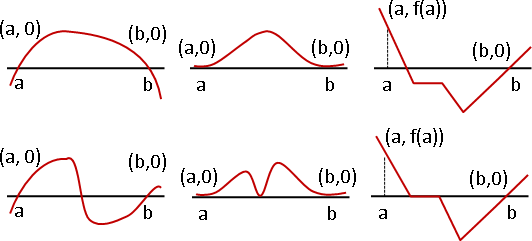
另外，當[a,b]的端點恰好沒有定義在f(x)當中，則無法計算出f(a)和f(b)的值。要解決這個問題，可以將區間略微縮小一些，像是[a + 0.001, b - 0.001]，即可避免端點沒有定義的情況。

二分法

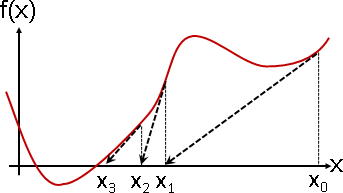
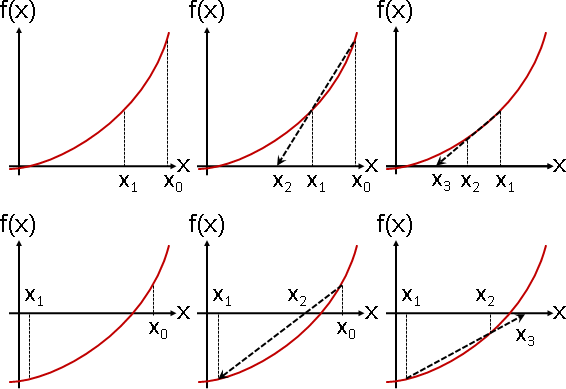
區間切兩半，縮小區間，夾擠根，逼近根。

遞迴下去，直到區間足夠微小。

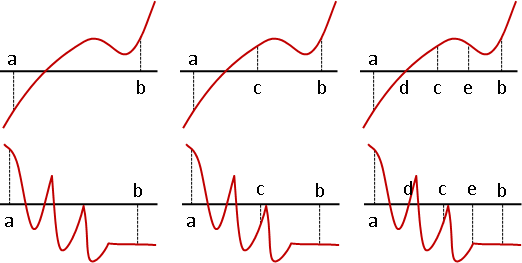
找到一個根

左右兩個區間都處理，結果跟窮舉法沒兩樣。

不如只處理其中一個區間吧！只處理確定有根的區間，即f(a)和f(b)異號的區間。如果左右兩個區間都確定有根，那麼就只處理左邊區間。這正是binary search。

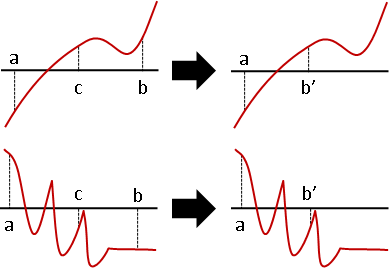
f(a)和f(b)同號的區間，放棄處理，不確定是否有根。f(a)和f(b)為零的區間，中止處理，顯然已經找到一個根。f(a)和f(b)異號的區間，繼續處理，二分尋找根。

最小精確度

二分越多次，答案越精確。

float變數、double變數，能夠儲存的位數有限，不可能精確，有著一個極限。不斷分割區間，就能到達極限。一個float變數的範圍約為10³⁸到10⁻³⁸，分割區間log₂10⁷⁶ ≈ 252次，定能得到float變數所能儲存的最精確的數值。

float bisection(float a, float b, float (*f)(float)) { float fa = f(a), fb = f(b), c, fc; while (true) // 到達精確的極限 { c = (a + b) / 2; if (a == c || b == c) break; fc = f(c); if (fc == 0) break; if (fa * fc < 0) {b = c; fb = fc;} else {a = c; fa = fc;} } return c; }

據我測試，不管迴圈計算多少遍，a b的大小關係永遠不變，而c永遠會在[a,b]當中，不會超出範圍。

迴圈不斷計算之後，有些函數造成a b最終相等，也有些函數造成a b永遠不相等，永遠相差一個最小精確度的值。要解決不相等的問題，只需判斷c是a或是b即可。

自訂精確度

[a,b]寬度大於自訂精確度，就繼續分割區間。[a,b]寬度小於等於自訂精確度，就立即停止迴圈。因為c永遠在[a,b]當中，所以c的誤差不超過自訂精確度。

如此一來，得以減少迴圈次數，不必做到252次。

const int ε = 1e-6; // 精確度（誤差範圍） float bisection(float a, float b, float (*f)(float)) { float fa = f(a), fb = f(b), c = a, fc; while (b - a > ε) // 不夠精確就繼續 { c = (a + b) / 2; fc = f(c); if (fc == 0) break; if (fa * fc < 0) {b = c; fb = fc;} else {a = c; fa = fc;} } return c; }

找到所有根

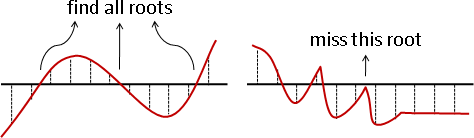
整條數線細分成許多微小區間。f(a)和f(b)同號的區間，視作沒有根；f(a)和f(b)為零的區間，視作只有端點有根；f(a)和f(b)異號的區間，視作剛好有一個根，實施二分法找到根。

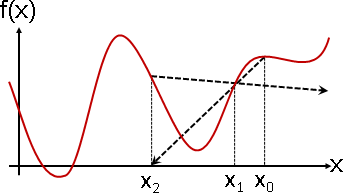
只要細分的足夠細膩，理論上可以找到所有根，除了一種例外：根恰好是局部極值。此時必須配合其他的求根方法，才能處理這個例外。

void roots(float (*f)(float)) { float width = 100; // 微小區間的寬度 // 假設所有根都在-100000到+100000之間 for (float x = -1e5; x < +1e5; x += width) { if (f(x) == 0) cout << x; // x是根 if (f(x) * f(x + width) < 0) cout << bisection(x, x + width, f); } }

範例：求平方根

int sqrt(int x) { int a = 1, b = x; while (a <= b) { // int c = (a + b) / 2; int c = a + (b - a) / 2; // 防止溢位 if (c * c == x) return c; else if (c * c > x) b = c - 1; else a = c + 1; } return b; }

遞增函數

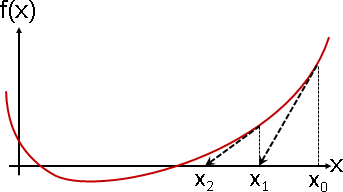
連續遞增（減）函數，若有根，保證能找到根。

二分法不斷地縮小根的範圍。

牛頓法

一張圖勝過千言萬語。

範例：求平方根

x = sqrt(n)
x² = n
x² - n = 0
f(x) = x² - n
f′(x) = 2x

float sqrt(float n) { float x = 0.5f * n; // x₀ for (int i=0; i<5; ++i) { // x = x - f(x) / f′(x) // x = x - (x * x - n) / (2.f * x); x = 0.5f * (x + n / x); } return x; }

凸函數

斜率是連續遞增（減）函數，若有根，保證能找到根。

以斜率的觀點來看，牛頓法不斷地縮小斜率範圍。

割線法

牛頓法採用切線，割線法採用割線。

缺點：遞推次數更多、計算步驟更多。優點：不用微分。

一開始選定的兩點，如果不夠靠近根，割線可能會亂跑。

運氣不好時，割線呈水平線，割線法會故障；割線趨近水平線，下一點會溢位。

fixed point（fixpoint）

找到確切的輸入數值，讓輸出和輸入完全一樣。這樣的輸入稱作「不動點」。可能有許多個，也可能不存在。

以函數圖形表達函數的不動點：當輸入變數只有一個，是函數曲線與直線y = x的相交之處。當輸入變數超過一個，此處不討論。

eigenpoint【尚無正式名稱】

找到確切的輸入數值，讓輸出是輸入的倍數，倍數是某個定值。這樣的輸入稱作「特徵點」。可能有許多個，也可能不存在。

以函數圖形表達函數的特徵點：當輸入變數只有一個，是函數曲線與直線y = λx的相交之處。當輸入變數超過一個，此處不討論。

求根、求不動點、求特徵點，本質上是同一件事情。

求根變成求不動點：等號兩邊同時加上x。求不動點變成求根：等號兩邊同時減去x。

f(x) = 0   <--->   f(x) + x = x   <--->   g(x) = x

求根變成求特徵點：再乘上任意倍率。求特徵點變成求根：反向操作。

f(x) = 0   <--->   λ (f(x) + x) = λx   <--->   h(x) = λx

只要知道怎麼求不動點、特徵點，就能求根。碰巧的是，不動點擁有高速演算法！

不動點遞推法

不斷代入上次求得的數值。就這麼簡單。

即是在函數圖形與45°斜線之間往返。越走越小圈、越走越近。

運氣不好時，無法得到不動點。

越走越大圈、越走越遠。

程式碼很短，只有一個迴圈。

float fixedpoint(float (*f)(float)) { float x = random(); // 隨便設定一個起點 float y = f(x); int t = 0; while (x != y) // 直到遇到不動點 { x = y; // 不斷代入上次求得的數值 y = f(x); // 運氣不好時，無法得到不動點。 if (++t > 1000) return 1e9; } return x; }

收縮函數：斜率絕對值小於1的連續函數

遭遇不動點，其中一種情況，就是步伐越來越短。測量X軸方向的步伐大小，即是x₀ x₁ x₂……之間的間距。當間距越來越小，最後xₜ = xₜ₊₁ = f(xₜ)趨近相等，遭遇不動點xₜ。

此處只討論這種情況。

|x₁ - x₀| > |x₂ - x₁| > |x₃ - x₂| > ......

|x₁ - x₀| > |x₂ - x₁|   此處以開頭兩項為例。事實上任意相鄰兩項都成立。

|x₁ - x₀| > |f(x₁) - f(x₀)|

    |f(x₁) - f(x₀)|   
1 > ——————————————— = |slope|
       |x₁ - x₀|      

|slope| < 1

-1 < slope < 1

先後間距變小，移項之後，割線斜率介於±1。

也就是說，一個連續函數，任意兩點的割線的斜率的絕對值都小於1，保證有不動點。無論起點在哪裡，都能找到不動點。

換句話說，切線的斜率的絕對值都小於1。不太斜的連續函數。

特徵點遞推法

在函數圖形與斜率λ的直線之間往返。上次求得的數值，除以λ之後才代入。

平緩函數：斜率絕對值小於|λ|的連續函數

遭遇特徵點，其中一種情況，就是步伐越來越短。中略。割線的斜率介於±λ。

|x₁ - x₀| > |x₂ - x₁| > |x₃ - x₂| > ......

|x₁ - x₀| > |x₂ - x₁|   此處以開頭兩項為例。事實上任意相鄰兩項都成立。

|x₁ - x₀| > |f(x₁/λ) - f(x₀/λ)|   上次求得的數值，除以λ之後才代入。

|λχ₁ - λχ₀| > |f(χ₁) - f(χ₀)|     變數代換

|λ| |χ₁ - χ₀| > |f(χ₁) - f(χ₀)|

      |f(χ₁) - f(χ₀)|   
|λ| > ——————————————— = |slope|
         |χ₁ - χ₀|      

|slope| < |λ|

-|λ| < slope < |λ|               介於±λ

equation

由未知數（變數）、已知數（常數）的各種運算來構成式子。兩個相等的式子，就叫作「方程式」。

2x + 1 = (4x² + 3) / (x - 1)

方程二字借自中國古代數學書籍，意義相去甚遠，是個不精準的翻譯。按照英文字面意義來翻譯，應該稱作「等式」才對。

中學數學教了很多方程式的計算，例如解一元二次方程式、解聯立方程式，並且搭配幾何學一起講解。大學指考前，算了千百次，應當難不倒各位。

方程式有什麼用途呢？其實就是設x、解x。這兩件事情很難用中文講個明白，不過只要經歷許多數學題目之後，自然而然就能體會到設x、解x的精神所在。

求根、求不動點、求特徵點、求解，本質上是同一件事情。

方程式重新整理成函數的模樣，就能求解。

2x + 1 = (4x² + 3) / (x - 1)

等量減法公理，兩邊同減一樣多的東西。（移項）
2x + 1 - (4x² + 3) / (x - 1) = 0

整理成函數的模樣，然後求根即可！
f(x) = 2x + 1 - (4x² + 3) / (x - 1)

方程式重新整理成函數的模樣，就能以各種姿勢求解。

f(x) = 0                                  root
f(x) + x = x          --->  g(x) = x      fixed point
λf(x) + λx = λx       --->  h(x) = λx     eigenpoint
λf(x) + λq(x) = q(x)  --->  p(x) = q(x)   solution

UVa 358 10341 10428 10566 10668 11277

容易求根、求不動點、求特徵點、求解的函數類型

increasing function：遞增函數。輸入變大，輸出跟著變大（或不變）。斜率是正數（或零）。適合bisection method。

convex function：凸函數。隨便劃一道割線，函數曲線總是凹下去（或平貼）。斜率是遞增函數。適合Newton's method。

Lipschitz function：平緩函數。隨便劃一道割線，斜率的絕對值小於（或等於）一個定值。適合fixed point iteration。

polynomial function：多項式函數。可以手工推導公式解，也可以使用上述演算法求解。

大家習慣改成嚴格版本、去掉等號，讓函數曲線不會平貼座標軸、不會產生無限多根。

system of equations（simultaneous equations）

許多道方程式同時成立，整體稱作「方程組」或者「聯立方程式」。

⎧ 1 x + 2 y - 4 sin(z) = 1
⎨ 2 x - 4 y + 2 cos(z) = 2
⎩ 3 x + 1 y + 1 exp(z) = 3

inequality（inequation）

「不等式」。等號=改成了小於<、大於>、小於等於≤、大於等於≥、不等於≠。

2x + 1 < (4x² + 3) / (x - 1)

system of inequalities

「不等式組」、「聯立不等式」。許多道不等式同時成立。

⎧ 1 x + 2 y - 4 sin(z) < 1
⎨ 2 x - 4 y + 2 cos(z) ≤ 2
⎩ 3 x + 1 y + 1 exp(z) > 3

不等式可以重新整理成函數的模樣。

大於可以重新整理成小於。

⎧  1 x + 2 y - 4 sin(z) - 1 < 0          ⎧ f(x,y,z) < 0
⎨  2 x - 4 y + 2 cos(z) - 2 ≤ 0   --->   ⎨ g(x,y,z) ≤ 0
⎩ -3 x - 1 y - 1 exp(z) + 3 < 0          ⎩ h(x,y,z) < 0

constraint satisfaction

「約束滿足」。許多道等式與不等式同時成立。