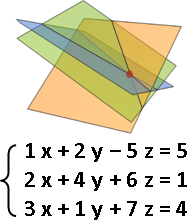
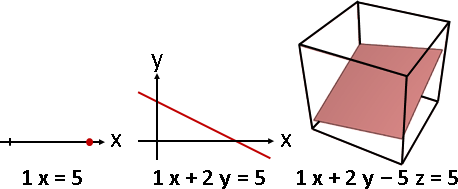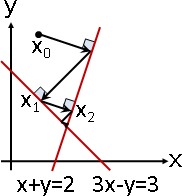linear equation: elimination
等量公理
相信大家已經學過如何解一次方程組:由上往下消除變數,變成階梯狀;由下往上解出變數,變成對角線。
由上往下消除變數的過程,就叫做「高斯消去法」。
演算法(Gaussian elimination)
一個矩陣,化成上三角矩陣,對角線元素皆為一。
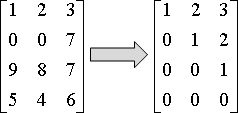
由上往下,處理每個橫條,實施三種運算:交換、倍率、相減。
如果橫條的首項係數不是零,以該橫條抵銷下方橫條,令下方橫條的首項係數化成零。如果是零,就往下找到非零橫條,先交換,再抵銷。
pivot row:首項係數不是零的橫條。 pivot:上述橫條的首項係數。 pivoting:找到pivot row,視情況進行交換。
減少誤差的方法:取絕對值最大的pivot row,抵銷其餘row。換句話說,首項係數絕對值最大的橫條,總是交換到上方,再來抵銷下方橫條。倍率小於1,相減誤差少。
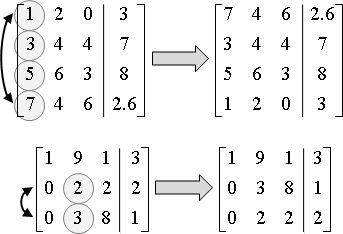
矩陣邊長N×M,時間複雜度O(N²M)。大家習慣討論方陣,N = M,時間複雜度O(N³)。
方陣的高斯消去法,程式碼如下所示。矩陣的高斯消去法,留給大家自行練習。
解一次方程組
首先實施高斯消去法,求得上三角矩陣。
由下往上,處理每個橫條。把先前解出的變數,代入到目前橫條,解出變數。時間複雜度O(N²)。

UVa 10109 10524 10828 ICPC 3563
演算法(Gauss–Jordan elimination)
「高斯喬登消去法」是延伸版本。對角線化成一、其餘化成零。
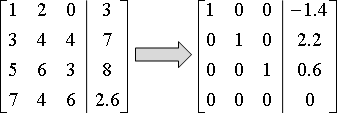
時間複雜度仍是O(N³)。
高斯喬登消去法也可以解一次方程組,但是步驟數量比較多。主要用途是求反矩陣。
求反矩陣
利用「高斯喬登消去法」。

求determinant
利用「高斯消去法」,對角線不化成一,保留原有數字。
上三角矩陣,對角線元素的乘積,便是determinant。
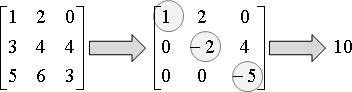
如果矩陣裡都是整數,那麼determinant也是整數。想避免浮點數誤差,可以使用輾轉相除法進行消去。時間複雜度O(N³logC),C是絕對值最大的首項係數。
UVa 684
LU decomposition
高斯消去法可以改寫成LUP分解!時間複雜度O(N³)。
交換橫條、抵銷橫條,可以改寫成矩陣乘法。一連串交換橫條、抵銷橫條,可以整併成三個矩陣連乘:下三角矩陣L、上三角矩陣U、列交換矩陣P。稱作「LUP分解」。
如果恰好都沒有交換橫條,則可忽略P。稱作「LU分解」。
LU分解的用途是解大量一次方程組Ax = b,A固定,b有許多組。這種情況下,LU分解,每次求解需時O(N²);高斯消去法,每次求解需時O(N³)。
Cholesky decomposition
「對稱正定矩陣symmetric positive definite matrix」:特徵值均為正數。
對稱正定矩陣的LU分解。L與U將互相對稱。
時間複雜度仍是O(N³),但是步驟數量較少。