function network - 演算法筆記

function network🚧

function network（computational graph）

函數：輸入多個數值，輸出一個數值。

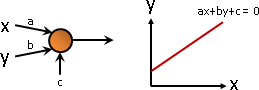
計算學家擅長線性函數、多項式函數。以下以一次函數為例。

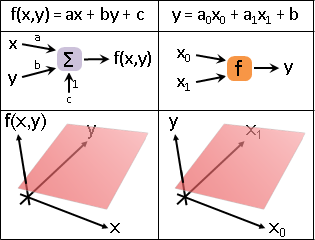
函數網路：形成網路。可以宏觀地視作一個函數。

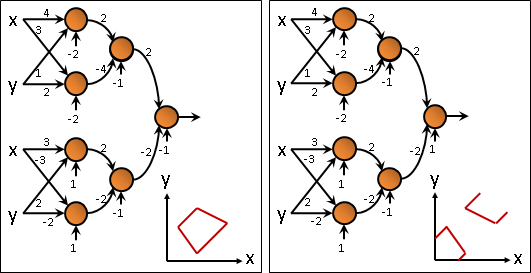
計算學家擅長樹、有向無環圖。以下以分層圖為例。

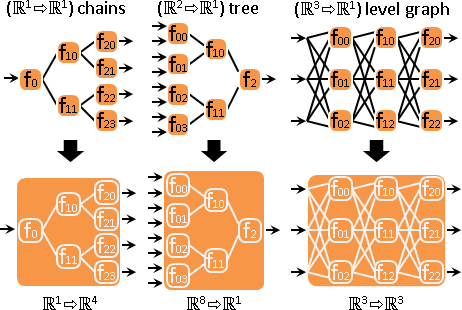
一次函數不斷串接，仍是一次函數。

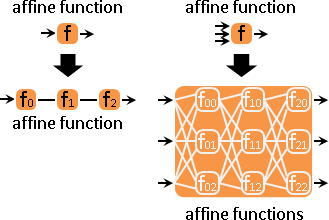
function network運算

函數網路按理可以定義加減乘除微積運算，可以求根、求解、求極值，可以用於迴歸、內插、擬合、分群、分類。

不過這些運算仍在研究當中，尚未定義。

求值

函數：代入x，求得y。

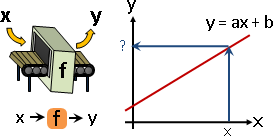
函數鏈：按照順序，每個函數各自求值。

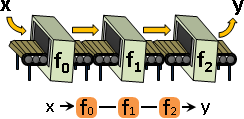
函數網路：按照層級順序、拓樸順序，每個函數各自求值。

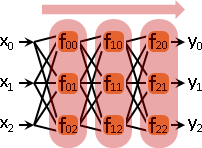
求根

全部展開之後，等同於解一次方程組。目前沒有演算法。

最佳化

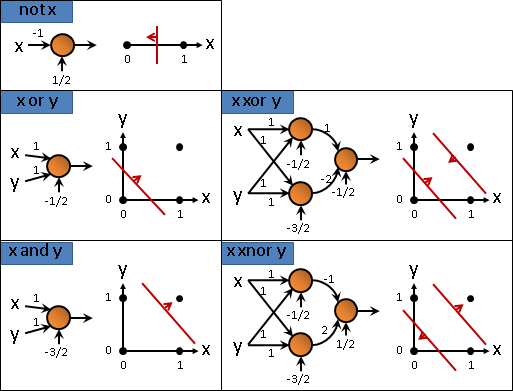
函數：一次函數，呈直線，極值在無限遠處，沒有討論意義。

話雖如此，但這裡還是介紹一下最佳化演算法，以鋪陳後文。

一次函數可以一次微分，適用梯度下降法。朝梯度方向走會上升、得極大值，朝梯度反方向走會下降、得極小值。

函數鏈：展開之後仍是一次函數。

沿總梯度方向走。梯度是「f(x)變化」和「x變化」的比值。總梯度是「f(...f(x))變化」和「x變化」的比值。梯度逐層連乘，得到總梯度。

另外介紹一個畫蛇添足的方法：最內層x走一步，每一層x也都跟著走一步。

梯度是「f(x)變化」和「x變化」的比值，乘以梯度估得外層步伐大小，除以梯度估得內層步伐大小。當f是一次函數、呈直線，則步伐大小精準無誤。

函數網路：由兩種情況混合而成。

一、多到一。多個函數的輸出，是同一個函數的輸入。

整體視作一個函數。每條路線分別統計總梯度。根據輸入維度，取得梯度維度。數學術語是partial derivative。

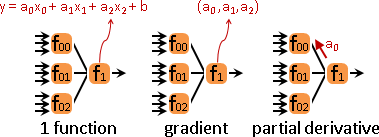
二、一到多。同一個函數的輸出，是多個函數的輸入。

一條路線視作一個函數。函數們相加合併。梯度們也跟著相加合併。數學術語是multiobjective optimization與scalarization。

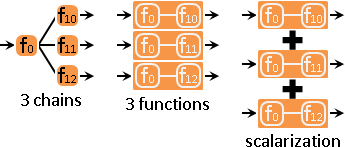
函數網路化作函數鏈，函數鏈化作函數，函數們相加合併，求得總梯度，實施梯度下降法。

一、任意多項式函數：函數用於複合再總和＝函數的總和用於複合。窮舉每條路線，逐條合併函數＝逆拓樸順序，逐層合併函數。

二、任意可微函數：函數的總和的梯度＝函數的梯度的總和。窮舉每條路線，逐條合併梯度＝逆拓樸順序，逐層合併梯度。

逐條合併化作逐層合併。數學術語是distributive law。

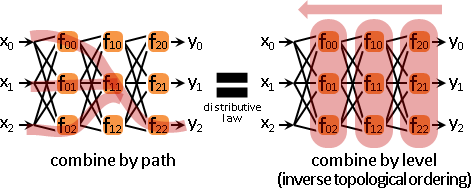
拓樸順序，求得每個函數的x值。逆拓樸順序，統計每個函數的總梯度。第一層函數各自沿總梯度方向走、得極大值。

const int D = 10;	// 深度（層數）
const int B = 10;	// 廣度（每層的函數數量）
Function f[D][B];	// 函數網路

vector<float>& operator+=(vector<float>& a, vector<float>& b)
{
	for (int i=0; i<a.size(); ++i) a[i] += b[i];
	return a;
}

vector<float>& operator*=(vector<float>& a, float b)
{
	for (int i=0; i<a.size(); ++i) a[i] *= b;
	return a;
}

void gradient_descent()
{
	float x[B];
	for (int i=0; i<B; ++i)
		x[i] = random(-∞, +∞);

for (float step = 1.0; step > 1e-5; step *= 0.9)
	{
		// forward：計算每個函數的x值
		for (int i=0; i<D; ++i)
			for (int j=0; j<B; ++j)
			{
				Function& p = f[i][j];
				if (i == 0)
					for (int k=0; k<B; ++k)
						p.x[k] = x[k];
				else
					for (int k=0; k<B; ++k)
						p.x[k] = f[i-1][k].y;

p.y = p.b;
				for (int k=0; k<B; ++k)
					p.y += p.a[k] * p.x[k];
			}

// backward：計算總梯度
		for (int i=D-1; i>=0; --i)
			for (int j=0; j<B; ++j)
			{
				Function& p = f[i][j];
				if (i == D-1)
					// vector size B
					p.gsum = p.gradient(p.x);
				else
				{
					// 函數的梯度的總和
					float gsum = 0;
					for (int k=0; k<B; ++k)
						gsum += f[i+1][k].gsum[k];
					p.gsum = p.gradient(p.x);
					p.gsum *= gsum;
				}
			}

// 第一層走一步
		for (int j=0; j<B; ++j)
			x[j] += f[0][j].gsum[j] * step;
	}

for (int i=0; i<B; ++i)
		cout << x[i];
}

內插

古代有一種做法叫做radial basis function network。

迴歸

函數：迴歸函數是一次函數，即是一次迴歸。

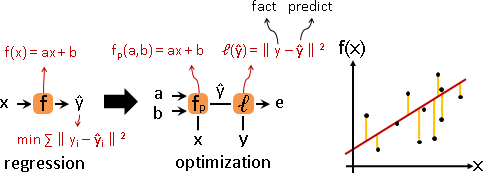
化作最佳化問題，實施梯度下降法。

函數末端接上平方誤差函數。函數的變數與係數，角色互調。

先前小節的各種性質，一次函數換成多項式函數，性質依然成立。平方誤差函數是多項式函數，最佳化依然堪用。

平方誤差函數是拋物線函數（凸函數）。誤差總和是拋物線函數總和，仍是拋物線函數。有唯一最小值，沒有鞍點，有公式解。

大量數據的最佳化演算法，衍生兩種版本offline和online，又叫做batch和stochastic。實務上使用online版本，優點是數據存取時間大幅降低，缺點是答案不太正確。

函數鏈：展開之後，仍是一次迴歸。

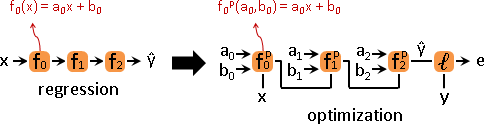
函數鏈展開、迴歸函數，兩邊的係數一一對應，顯然有解。函數鏈係數太多，導致多解。嘗試尋找其中一解。沿用梯度下降法：

正向求得每個函數的x值。逆向統計每個函數的總梯度。每個函數各自沿總梯度反方向走，求得每個函數的係數。

梯度下降法可以找到其中一解嗎？這是懸案！

若已知x值，則ab擁有唯一解。可是必須先利用ab才能求得每個函數的x值──雞蛋悖論，給x求ab，給ab求x。也許它們成對收斂，宛如EM algorithm，我不是很確定。【尚待確認】

函數網路：許多個一次迴歸。誤差合一，乍看相關，實則獨立。

梯度下降法此時又稱作「反向傳播法backpropagation」：

拓樸順序，求得每個函數的x值。逆拓樸順序，統計每個函數的總梯度。每個函數各自沿總梯度反方向走，求得每個函數的係數。

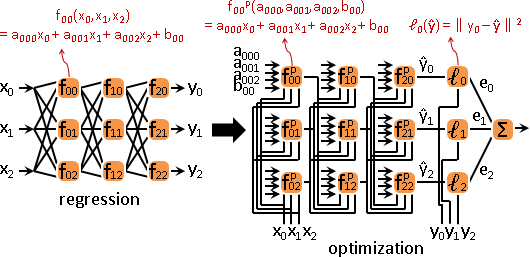
另一種觀點：每個函數各自迴歸。

逆拓樸順序，統計每個函數的總誤差。總誤差是後繼函數的誤差的加權總和，權重是後繼函數的梯度、亦是係數（一次函數）。

當權重均為正數，則總誤差是橢圓拋物面函數elliptic paraboloid。有唯一最小值，沒有鞍點，有公式解。【尚待確認】

正常情況下，權重不見得均為正數。後面章節將介紹一種特別的函數ReLU，當後繼函數梯度過小，強制權重為零。【尚待確認】

scalarization vs. 數據誤差總和。平方誤差函數的梯度是一次函數。【待補文字】

反向傳播法可以找到其中一解嗎？這是懸案！

const int D = 10;		// 深度（層數）
const int B = 10;		// 廣度（每層的函數數量）
Function f[D][B];		// 函數網路

const int N = 100;		// 數據數量
float x[N][B], y[N][B];	// 數據

void backpropagation()
{
	// 隨便挑選起點
	for (int i=0; i<D; ++i)
		for (int j=0; j<B; ++j)
		{
			Function& p = f[i][j];
			for (int k=0; k<B; ++k)
				p.a[k] = random(-∞, +∞);
			p.b = random(-∞, +∞);
		}

// online
	for (int n=0; n<N; ++n)
	{
		// 數據(x[n], y[n])實施梯度下降法
		// 誤差越來越小，大可不必刻意調整步伐，只需足夠步數。
		// 當數據足夠多、足夠準，甚至只需各走一步。
		const float step = 1.0;

// forward：計算每個函數的x值
		for (int i=0; i<D; ++i)
			for (int j=0; j<B; ++j)
			{
				Function& p = f[i][j];
				if (i == 0)
					for (int k=0; k<B; ++k)
						p.x[k] = x[k];
				else
					for (int k=0; k<B; ++k)
						p.x[k] = f[i-1][k].y[k];

p.y = p.b;
				for (int k=0; k<B; ++k)
					p.y += p.a[k] * p.x[k];
			}

// backward：計算總梯度
		for (int i=D-1; i>=0; --i)
			for (int j=0; j<B; ++j)
			{
				Function& p = f[i][j];
				if (i == D-1)
					p.sgsum = -2 * (y[n] - p.y);
				else
				{
					// 函數的梯度的總和，改成了平均數。
					p.sgsum = 0;
					for (int k=0; k<B; ++k)
						p.sgsum += f[i+1][k].sgsum
								 * f[i+1][k].a[k];
					p.sgsum /= B;
				}
			}

// 梯度下降法：沿總梯度反方向前進、得極小值
		for (int i=D-1; i>=0; --i)
			for (int j=0; j<B; ++j)
			{
				Function& p = f[i][j];
				for (int k=0; k<B; ++k)
					p.a[k] -= p.sgsum * p.x[k] * step;
				p.b -= p.sgsum * 1 * step;
			}
	}
}

根據一次方程組演算法「Gauss–Seidel iteration」，剛出爐的新梯度，馬上傳播，也許可以加快收斂速度。【尚待確認】

函數網路太深，總梯度巨大與渺小，浮點數溢位與歸零。解法是數據預先正規化：減去平均數、除以標準差，讓數值接近[-1,+1]。如此一來，迴歸函數的係數、亦是梯度，也自然而然正規化了。關鍵字vanishing gradient problem與batch normalization。

承上，scalarization，梯度總和也改成梯度平均數。

函數網路迴歸，幾何意義不明。也許是階層迴歸：每個函數，網羅總截距，實施總迴歸。【尚待確認】

順便補充一下。各筆數據的x值，一齊實施仿射變換（一次函數），平行、共線、凹凸保持不變。總迴歸的x值，這些性質完好如初。

擬合

函數網路方程式，幾何意義不明。點到它的距離，如何定義呢？

變換

函數網路就是對數據實施一連串變換。

一個有趣的觀點是摺紙：

一個有趣的觀點是流形：

neural network🚧

neural network

「神經網路」是一種特別的函數網路。

神經網路的各種運算當中，只有迴歸獨領風騷，如日中天。因此本篇文章只講迴歸。

一次函數：𝑓(x₀, x₁, ...) = a₀x₀ + a₁x₁ + ... + b

一次方程式：𝑓(x₀, x₁, ...) = a₀x₀ + a₁x₁ + ... + b = 0

一次函數：𝑓(x⃗) = a⃗ ᵀx⃗ + b

一次方程式：𝑓(x⃗) = a⃗ ᵀx⃗ + b = 0

註：有人把數值x₀, x₁, ...合在一起，簡寫成向量x⃗。

註：由於外觀宛如加權平均數，因此有人把a寫成w。

註：一次函數不是線性函數，前者多了常數項。

一次方程式的幾何意義是超平面！

一維空間的點：ax + b = 0

二維空間的直線：a₀x₀ + a₁x₁ + b = 0

三維空間的平面：a₀x₀ + a₁x₁ + a₂x₂ + b = 0

任意維空間的超平面：a₀x₀ + a₁x₁ + a₂x₂ + ... + b = 0

註：中學數學習慣寫成ax+by+c=0、ax+by+cz+d=0。本文當中，由於維度太多，只好重編符號。

點線距離函數：𝒹(x₀,x₁) = (a₀x₀ + a₁x₁ + b) / √a₀² + a₁²

直線函數：𝑓(x₀,x₁) = a₀x₀ + a₁x₁ + b

單位步階函數：𝓊(x) = (x < 0) ? 0 : 1

原本是想談任意的一次函數，以下以直線函數為例。

直線有正反側，點線距離有正負號。點線距離代入𝓊，得到正側或反側。

直線擬合（二維）：arg mina⃗,b ∑i ‖ 𝒹(x⃗ᵢ) ‖²

一次分類（二維）：arg mina⃗,b ∑i ‖ cᵢ - 𝓊(𝒹(x⃗ᵢ)) ‖²

一次迴歸（三維）：arg mina⃗,b ∑i ‖ yᵢ - 𝑓(x⃗ᵢ) ‖²

已知大量點座標x⃗ᵢ、渴望的類別cᵢ、渴望的截距yᵢ，請找到一個直線函數，盡量符合已知條件，令誤差平方總和越小越好。

一次分類當中，𝒹的分母√a₀² + a₁²不影響正反側判斷，無作用、可省略。因此𝒹可以簡化成𝑓。

註：數學家沒有定義「直線函數」。本文的定義是我逕自調配的，請小心服用。眼尖讀者應該發現了本站文件存在兩種不同定義：點線距離，直線函數是標準式𝑓(x₀,x₁) = a₀x₀ + a₁x₁ + b；一次迴歸，直線函數是斜截式f(x) = ax + b。不要搞混囉！

活化函數：𝜙(x)

神經元：𝜙(𝑓(x⃗))

神經網路：𝜙(𝑓(x⃗))相互銜接，成為函數網路。

直線函數，接上活化函數，合稱神經元。神經元相互銜接，合稱神經網路。這些概念起初是藝術創作來的，不是邏輯推理來的，因此名稱非常奇葩。

神經元迴歸：arg mina⃗,b ∑i ‖ yᵢ - 𝜙(𝑓(x⃗ᵢ)) ‖²

迴歸函數是神經元。統合了一次分類、一次迴歸。

𝜙(x) = (x < 0) ? 0 : 1是一次分類。𝜙(x) = x是一次迴歸。𝜙(x) = (x < 0) ? 0 : x是一次迴歸限制範圍，關注正側、冷落反側。𝜙(x) = eˣ / (eˣ + 1)或𝜙(x) = (e²ˣ + 1) / (e²ˣ - 1)是一次迴歸限制範圍，關注inlier、冷落outlier。【尚待確認】

損失函數：𝓁(ŷ;y)

神經元迴歸：arg mina⃗,b ∑i 𝓁(𝜙(𝑓(x⃗ᵢ));yᵢ)

誤差可以寫成函數的形式。𝓁(ŷ;y) = ‖ y - ŷ ‖是絕對值誤差。𝓁(ŷ;y) = ‖ y - ŷ ‖²是平方誤差。

註：古人將「誤差函數」這個詞彙作為erf(x)，今人只好另起一名「損失函數」作為誤差的函數。

一筆數據的誤差：𝓁(𝜙(𝑓(x⃗));y)

直線函數．改：𝑓ₚ(a⃗,b;x⃗) = a₀x₀ + a₁x₁ + b

最小化誤差：arg mina⃗,b 𝓁(𝜙(𝑓ₚ(a⃗,b;x⃗));y)

因為沒有公式解，所以迴歸問題化作最佳化問題。

實施梯度下降法，求得a₀ a₁ b。函數𝑓暨參數x₀ x₁，改成了函數𝑓ₚ暨參數a₀ a₁ b。總梯度是∇𝑓ₚ ∇𝜙 ∇𝓁相乘。

𝑓ₚ(a₀,a₁,b) = a₀x₀ + a₁x₁ + b	∇𝑓ₚ(a₀,a₁,b) = [x₁,x₂,1]ᵀ
𝜙(x) = (x < 0) ? 0 : x        	∇𝜙(x) = (x < 0) ? 0 : 1
𝓁(ŷ) = (y - ŷ)²             	∇𝓁(ŷ) = -2 (y - ŷ)

多筆數據的誤差：∑i 𝓁(𝜙(𝑓(x⃗ᵢ));yᵢ)

最小化誤差：arg mina⃗,b ∑i 𝓁(𝜙(𝑓ₚ(a⃗,b;x⃗ᵢ));yᵢ)

梯度下降法衍生兩種版本。實務上用online版本。

offline：一次梯度下降法，梯度是∇(𝓁∘𝜙∘𝑓ₚ)(x⃗₀) + ∇(𝓁∘𝜙∘𝑓ₚ)(x⃗₁) + ...。每一步都用到所有數據，數據存取數輪。

online：數次梯度下降法，第一次∇(𝓁∘𝜙∘𝑓ₚ)(x⃗₀)，第二次∇(𝓁∘𝜙∘𝑓ₚ)(x⃗₁)，……。每一次只用到一筆數據，數據存取一輪。

神經網路迴歸：𝜙(𝑓(x⃗))網路實施迴歸。

神經元迴歸採用梯度下降法。神經網路迴歸也是採用梯度下降法（反向傳播法）：逆拓樸順序，統計總梯度，每個神經元各自沿著總梯度方向前進。另一種等價觀點：逆拓樸順序，統計總誤差，每個神經元各自迴歸。

總誤差是各誤差的加權總和，權重是後繼函數梯度。

一、活化函數ReLU：其梯度是左半0、右半1。總誤差是拋物線函數，左半輾平成零，右半仍有唯一最小值，沒有鞍點，有公式解。【尚待確認】

二、活化函數sigmoid：總誤差沒有規律。似乎擁有很多丘陵，妨礙梯度下降。大家不使用也不討論。

三、活化函數SIREN：週期函數，似乎是頻域處理，適合二維圖片與三維模型。【尚待確認】

梯度下降法可以找到其中一解嗎？這是懸案！

即便找到其中一解、甚至找到唯一最小值，然而online版本四處跳坑、答案不太正確。因而衍生新問題：如何挑選數據、起點、步伐、神經元數量。俗稱「調整參數」或「調參」。

const int D = 10;	// 深度（層數）
const int B = 10;	// 廣度（每層的神經元數量）
struct Neuron {float a[2], b;} n[D][B];	// 神經網路

const int N = 10000000;	// 數據數量
float x[N][B], y[N][B];	// 數據

void neural_network_regression()
{
	// 隨便挑選起點
	for (int i=0; i<D; ++i)
		for (int j=0; j<B; ++j)
		{
			Neuron& p = n[i][j];
			for (int k=0; k<B; ++k)
				p.a[k] = random(-∞, +∞);
			p.b = random(-∞, +∞);
		}

// online
	for (int t=0; t<N; ++t)
	{
		const float step = 1.0;

// forward：計算每個函數的x值
		for (int i=0; i<D; ++i)
			for (int j=0; j<B; ++j)
			{
				// input
				if (i == 0)
					for (int k=0; k<B; ++k)
						n[i][j].x[k] = x[t][k];
				else
					for (int k=0; k<B; ++k)
						n[i][j].x[k] = n[i-1][k].y;

// evaluate
				Neuron& p = n[i][j];
				p.y = p.b;
				for (int k=0; k<B; ++k)
					p.y += p.a[k] * p.x[k];
				p.∇𝜙 = (p.y < 0) ? 0 : 1;
				p.y = (p.y < 0) ? 0 : p.y;
			}

// backward：計算總梯度
		for (int i=D-1; i>=0; --i)
			for (int j=0; j<B; ++j)
			{
				Neuron& p = n[i][j];
				if (i == D-1)
				{
					p.sgsum = -2 * (y[t][j] - p.y);
					p.sgsum *= p.∇𝜙;
				}
				else
				{
					p.sgsum = 0;
					for (int k=0; k<B; ++k)
						p.sgsum += n[i+1][k].sgsum
								 * n[i+1][k].a[k];
					p.sgsum /= B;
					p.sgsum *= p.∇𝜙;
				}
			}

// 梯度下降法：沿總梯度反方向前進、得極小值
		for (int i=D-1; i>=0; --i)
			for (int j=0; j<B; ++j)
			{
				Neuron& p = n[i][j];
				for (int k=0; k<B; ++k)
					p.a[k] -= p.sgsum * p.x[k] * step;
				p.b -= p.sgsum * 1 * step;
			}
	}
}

神經網路迴歸的幾何意義不明。也許是階層迴歸：每個函數，網羅總截距，實施總迴歸。【尚待確認】

當一個函數輸出負數或零，則ReLU輸出零，導致無視總截距、不更新梯度。當一個函數永遠輸出負數或零，則後繼神經元永遠無作用，俗稱dead neuron或dying ReLU。

y = a⃗ ᵀx⃗ + b，a⃗與b本來是增益和偏差，加上ReLU之後變成是增益和臨界值。

換句話說，ReLU有如開關，可以控制是否要實施總迴歸。然而開關機制目前沒有直觀的解釋。目前大家只觀測到有時候關關會永久關閉。也有人提出一些歪招，宣稱可以避免永久關閉，例如SELU。

ReLU接在函數後面、函數前面，效果一樣（最初的x值改成正數）。如果要將ReLU視作開關，那麼接在前面比較妥當。

loss function

損失函數除了平方誤差以外，還可以考慮各個輸出管道的誤差分布，衍生了損失函數softmax、cross entropy、focal loss。總之有了log/exp就似乎很厲害，而大家也都用得很開心，一片和諧。

回顧一下分類演算法「AdaBoost」：分類錯誤的數據，其數量乘上倍率，增加誤差，增加步伐大小。

反覆乘上倍率，呈指數成長，差不多等同於最初直接套用exp。也許這些損失函數擁有相同功效。【尚待確認】

image quality: SSIM  MS-SSIM
https://blog.csdn.net/u011875342/article/details/78036380

nlp quality: perplexity
https://blog.csdn.net/index20001/article/details/78884646

speech quality: PESQ
https://en.wikipedia.org/wiki/PESQ

3d model quality: visible surface discrepancy
http://cmp.felk.cvut.cz/sixd/workshop_2018/data/hodan_r6d_eccv18_talk.pdf

延伸閱讀：universal approximation theorem

當活化函數是sigmoid，神經網路可以逼近各種平滑函數。

根據Taylor series，多項式函數們的加權總和，可以逼近各種平滑函數。

當活化函數是sigmoid，函數鏈形成了一類平滑函數。而函數網路可以視作函數鏈們的加權總和、複合。此定理是說這類平滑函數的加權總和、複合，可以逼近各種平滑函數。

然而大家習慣使用ReLU而非sigmoid。況且我們也不知道神經網路應該怎麼接。神經網路迴歸結果也不保證得到理想的平滑函數。因此這定理目前沒什麼用處。

層層疊疊類型🚧

概論

接好接滿，又深又廣。

神經網路沒人知道怎麼兜。大家中二病發作，瘋狂亂接亂串，自創各種造型，想要改變世界。亂槍打鳥，窮舉試誤，已經發掘許多漂亮網路，卻無法用數學證明其結構是否合理，已然是藝術創作。

feedforward neural network（前饋神經網路）

深度：經古人實測，無論多少層，效果跟三層沒兩樣。

廣度：沒人知道正確數量應該是多少。

活化函數：sigmoid。

深層無效的原因也許是：

一、一次函數的函數網路，仍是一次函數。增加層數淪為白工。

二、接上sigmoid可以解決上述問題。然而sigmoid的功用是引入限制範圍，關注inlier、冷落outlier。當限制範圍過小，可導致迴歸函數鬆脫掉落，喪失迴歸功效。增加層數淪為白工。

三、係數太多，多解，結果不穩定。

ICPC 4359

convolutional neural network（卷積神經網路）

先備知識是「convolution」和「image filtering」。

深度：目前是100層上下。

廣度：沒人知道正確數量應該是多少。

活化函數：ReLU。

一次函數（點積與偏差）推廣成卷積。

卷積：窮舉各種移位量，並且實施點積。

卷積有效的原因也許是：可逆時，答案足夠漂亮。

點積：幾何意義是投影量projection。統計意義是相關程度correlation。
卷積：統計意義是兩個隨機變數（浮動數字）相加。也許具有機率圖模型的功效。

許多神經元共用同一組係數，只需畫成一個神經元。接成區塊。

等寬間隙可以遏止overtraining或說是overfitting。關鍵字dilated convolution。

跳著接可以做特別的影像處理。關鍵字non-local neural network。

輸入是圖片，則是二維卷積。二維卷積可以拆散成一維卷積，最後再累加合併，降低時間複雜度。關鍵字google inception。

一次大範圍卷積、許多次小範圍卷積，效果差不多。神經元的係數是3x3、層數夠多，便足夠了。

經典版本是圖片辨識的VGGNet與RepVGG、物件偵測的R-CNN。

https://www.youtube.com/watch?v=ILsA4nyG7I0
http://cs231n.stanford.edu/syllabus.html
http://www.vision.rwth-aachen.de/media/course/WS/2015/computer-vision/cv15-part16-categorization4.pdf
http://kaiminghe.com/
http://www.rossgirshick.info/
http://chuansong.me/account/girlswhocode

dropout 去掉一些沒用的點
pooling 取總和或最大值
sparse momentum 各層刪除較小值，按比例重建
flatening 矩陣變向量

一種是二分資料，以data point為主角
一種是區域卷積，以pixel為主角
兩者之間應該有duality

residual neural network（殘差神經網路）

CNN改良版本。效果超群，原理不明。

難道是difference of Gaussian？

梯度下降法可以視作不動點遞推法。反向傳播法可以視作強化學習。難道是加上x的原因？

一次函數與ReLU，雙層似乎會形成山谷。難道是跳兩層的原因？

經典版本是圖片辨識的EfficientNet。

https://medium.com/@CinnamonAITaiwan/5eba5c8df7e4

電路設計類型🚧

概論

建立訊號迴路、建立功能模組。

recurrent neural network（遞迴神經網路）

製造迴圈，處理序列。好處是餘韻繞梁，壞處是難以計算。

學術前沿正在嘗試用CNN取代RNN。

經典版本是機器翻譯的LSTM network。

encoder–decoder network（編碼解碼網路）

先階層分解、再階層合成。

經典版本是物件偵測的RetinaNet、照片轉模型的volumetric CNN、語義布局圖片生成的cascaded refinement network。

generative adversarial network（生成對抗網路）

一個生成、一個判定。

經典版本是圖片轉譯的conditional GAN (pix2pix)、圖片轉譯的CycleGAN、圖片合成的deep convolutional GAN。

https://www.slideshare.net/yenlung/presentations
https://drive.google.com/file/d/1FJX4JIGuFd6kF-49vVSLyoXzaZRJeLdV
https://web.cs.hacettepe.edu.tr/~erkut/cmp717.s18/materials/w13-deep-generative-models.pdf

https://github.com/mit-han-lab/gan-compression

備忘

由於無法預測數據分布，因此任何事先指定的representation（例如sigmoid和kernel trick）都是沒有意義的。添加機率（例如貝氏學習）也是同樣沒有意義的。

個人推測正確的解法是：改變函數之間的輸入輸出連接方式。從最簡單的函數開始（例如線性函數），以函數的複合來得到各種特別的函數，或說是特別的representation。

一個值得關注的地方是將各種representation視作模組，經過適當突變（改變單一函數）、適當排列組合（改變階層架構）之後，可以得到更有用的模組。就好比人類發明機器的歷史過程。人類的智力架構可能也類似於此。

一個函數的輸出的重新排列組合，可以視作鏡射，鏡射是線性變換。至於函數之間的輸入輸出連接方式的重新排列組合，可以視作函數們複合一個線性函數。反過來說，函數的複合具備了重新排列組合的功效，而階層最佳化自然能找到適當的排列組合。

我就一介民科。以上僅供參考。

資料篩選類型🚧

attention neural network（注意神經網路）

篩選輸入：輸入向量與二進位向量相乘。

硬的：整數0與1。軟的：浮點數0到1。

可以取代RNN。

經典版本是機器翻譯的Google Transformer、XLNet，自然語言生成的BERT、GPT、BART。

http://akosiorek.github.io/ml/2017/10/14/visual-attention.html
https://medium.com/@cyeninesky3/dcc12d251449

memory neural network（記憶神經網路）

輸入分散儲存於記憶體，然後篩選記憶體。

經典版本是機器問答的MemN2N。

https://jhui.github.io/2017/03/15/Memory-network/

graph convolution network（圖卷積網路）

輸入是圖論的圖。

經典版本是圖片生成的image generation from scene graphs、知識表述的Deepmind Graph Nets。

neural network🚧

neural network visualization

有圖有真相。

比方來說，模仿電子電路的transfer function，我們可以測量神經網路每個節點的輸出直方圖，粗略判斷節點的功能。

https://distill.pub/2017/feature-visualization/
http://cnnlocalization.csail.mit.edu/
http://yosinski.com/deepvis
http://cs231n.github.io/understanding-cnn/

Netron
https://github.com/lutzroeder/Netron

neural network optimization

最佳化演算法收斂速度。

大家習慣使用的稱呼是hyperparameter optimization和hyperparameter tuning，俗稱調參。

例如寬度、層數、批量、最佳化演算法、步伐大小、……。

https://en.wikipedia.org/wiki/Neural_tangent_kernel

optuna
https://optuna.readthedocs.io/en/stable/tutorial/10_key_features/003_efficient_optimization_algorithms.html
https://www.cnblogs.com/Leo-Z/p/15963522.html
https://github.com/pfnet-research/optuna-book
https://takiba.net/

neural network compression

削減輸入、輸出、運算方式。

經典版本是XNOR-Net、AdderNet、ALBERT。

neural network distillation

神經網路改稱模型。收集資料暨調整參數改稱訓練。

已經完成訓練的大型模型，取其輸入輸出，重新訓練小型模型。

大家習慣使用的稱呼是knowledge distillation。

經典版本是DistilBERT。

s1: simple test-time scaling
https://github.com/simplescaling/s1
https://ithome.com.tw/news/167252
https://www.threads.net/@largitdata/post/DF2ieKavB-P

pretrained model與fine-tuning

已經初步訓練的模型，提供他人使用。他人可以自行加強訓練模型，作為其他用途。

知名商業產品HuggingFace Transformers、Llama、unsloth。一般來說，這類產品習慣提供多種模型，讓使用者選購試用。

mixture of experts

建立多種模型。觀察輸入，分配給適任的模型。適任的模型的加權平均值，作為輸出。

神經網路本身有許多層，就是為了做到這件事。現在改為設計一個任務分配器，直接做到這件事。

其實就是期刊主編審查論文的機制。其實就是演算法設計方法divide and conquer。其實就是資訊系統管理的load balancing。其實就是最佳化的ensemble averaging。

知名商業產品Mixtral 8x7B。

large language model與generative AI

專門用於自然語言處理的模型。專門用於生成資料的模型。這些都是商業術語，不是科學術語也不是工程術語。

Foundation Models for Natural Language Processing:
Pre-trained Language Models Integrating Media
https://link.springer.com/book/10.1007/978-3-031-23190-2

AI-Generated Content
https://zhuanlan.zhihu.com/p/615522634
https://arxiv.org/abs/2303.04226

Runway Gen-3 Alpha
https://x.com/runwayml/status/1834711758335779300

black-forest-labs Flux
https://x.com/nrehiew_/status/1820404554795802684
https://www.reddit.com/r/LocalLLaMA/comments/1ekr7ji/

neural network🚧

楔子

neuron與perceptron

生物學家、醫學家研究動物，發現了動物藉由神經來接收與傳達訊息，神經的基本單位是「神經元」。後來又發現，動物的大腦由大量神經元構成。

計算學家、數學家仿照神經元，發明了「感知器」，用來分類和預測事物。後來又發現，感知器其實就是一次分類器。

於是科學家大膽猜測：大腦似乎是一大堆一次分類器，思考似乎是一連串一次分類！科學家正在深入研究當中。

人格、行為、情緒、本能、直覺、天分、三觀、智力、智慧，這些抽象的心理概念，也許就是一堆一次分類器。

一大堆neuron與perceptron

神經元、感知器能做什麼事？

數學家發現感知器可以分類。一個感知器，製造筆直的分界線。一連串感知器，得以兜出各式各樣的分類效果，製造曲折的分界線。

這個發現相當重要。適當地排列組合感知器，就擁有辨識能力。大腦的辨識能力很可能源自於此！

數學家發現感知器可以算數學。一層可兜出邏輯運算NOT和AND和OR，兩層可兜出邏輯運算XOR和XNOR。進一步從邏輯運算兜出數值運算。進一步從數值運算兜出演算法。

這個發現相當重要。適當地排列組合感知器，就擁有判斷能力、計算能力。大腦的判斷能力、計算能力很可能源自於此！

大腦擁有大量神經元，應該得以進行非常深奧的推理，甚至超越邏輯所能描述的現象。例如由愛生恨、愛之深責之切、愛到深處無怨尤，大腦經常產出超乎理性的結論。

然而科學家迄今還不知道大腦的詳細結構。比如說「由愛生恨」的神經元如何連結呢？沒有人知道！科學家正在克服這個問題。

artificial neural network

「人工神經網路」、「類神經網路」。大量感知器串聯成網路，建立階層架構，模仿大腦！

然而我們往往不知道人工神經網路該兜成什麼樣子。於是大家捨難取易──選擇特定款式，藉由調整權重，達到分類效果。

真實神經網路，神經元會增生、死亡、重新連結。人工神經網路，格式固定，感知器不會增生、死亡、重新連結，分類效果較差。

為什麼不改成動態版本呢？因為時間複雜度。動態版本的計算量更加巨大，而現今計算機的計算力仍嫌不足。

近況

人工神經網路的潛力，遠遠超越目前的演算法，遠遠超越我們以窮舉法、分治法、動態規劃、貪心法所設計出來的演算法。最近電腦打敗人類圍棋冠軍，正是使用人工神經網路，棋風宛如真人。

學術單位正在研究人工神經網路的功效，公司行號正在製作人工神經網路的晶片。又由於分散式計算的崛起，計算機的計算力增加了，使得人工神經網路的研究略有進展。人工神經網路正夯。

各個領域的專家，也開始關注神經系統。關鍵字如neuroscience、neural computing、neural engineering，請讀者自行研究。

遠景

人工神經網路應該可以效仿編譯器自舉。我們總是用人腦設計演算法，既然人腦是神經元構成的網路、演算法是感知器構成的網路，理所當然我們能用人工神經網路設計人工神經網路。

學以致用、神來之筆，這些抽象的心理概念，也許就是自舉。

邏輯運算 → 數值運算 → 分類運算 → 算法

古人發明了邏輯運算（藉由電路），再用邏輯運算兜出數值運算（藉由二進位），再用數值運算兜出演算法（藉由流程圖）。至此是地球人的最新進度。

目前計算學家正在嘗試：用數值運算兜出分類運算（藉由數值分析），再用分類運算兜出演算法（藉由感知器）。讓我們拭目以待！

neural network🚧

備忘

日常生活中有些動作，身體已經習慣，自然而然可以完成，但是自己卻不知道詳細內情。

例如走路。走路時，其實不知道自己的腳究竟如何伸展。認真感受走路，反而能夠想出各種不同的走路方法。

更有甚者，一旦開始觀察詳細內情，就會暫時忘記原先習慣。

例如寫中文字。忽然要寫，寫得出來。但是如果仔細觀察拆解中文字，反而會變得不認識字，忘記怎麼寫。

備忘

「座標下降法」與「Gibbs取樣」非常相似，建立了最佳化與取樣的橋樑。

座標下降法非常類似於人類的處事方式，人類嘗試錯誤（取樣）而學習進步（最佳化）。迴歸、神經網路迴歸，或許可以用最佳化與取樣的思路來詮釋。

目前還沒有人仔細研究，我想這是一個好題目。

備忘

古代人的作法
假設 x 的出現機率呈 sigmoid function 或者 laplace distribution
因為獨立  所以所有 x 的出現機率是連乘積
用 maximum likelihood + gradient descent 來解

現代人的做法
把 sigmoid 改成 unit step
機率連乘積  取log變連加  這些過程通通精簡掉  直接變成 L₁-norm 最佳化
用 least squares (絕對值誤差改成平方誤差以利微分) + gradient descent 來解

如果我沒猜錯
1. 只要是 sigmoid / tanh  可以退化成 unit step
2. 機率學所謂的的獨立事件　可以退化成稀疏（L₀-norm 最佳化）
3. 引入機率的稀疏 sigmoid/tanh/laplace + maximum likelihood
　 退化成不含機率的稀疏

備忘

discrete choice model
softmax
sigmoid / logistic
https://stats.stackexchange.com/questions/204484/

synthetic control
https://taweihuang.hpd.io/2019/04/23/introduction-to-synthetic-control/

備忘

overview
https://zhuanlan.zhihu.com/p/51685063

application
https://www.zhihu.com/question/324428085/answer/683627711

seq2seq   (nl translation)
https://www.zhihu.com/question/59697263/answer/168866935

relation networks  (visual reasioning)
https://www.zhihu.com/question/60784169

encoder-decoder (2d to 3d)
http://aaronsplace.co.uk/papers/jackson2017recon/

equilibrium
https://www.zhihu.com/question/60374968/answer/189371146

domain adaptation
https://www.v7labs.com/blog/domain-adaptation-guide

AlphaGo Zero: tree + nn  (go game)
https://www.zhihu.com/question/66861459/answer/248588896

AlphaTensor: tree + nn + rl (matrix multiplication)
https://news.ycombinator.com/item?id=33096580

inception: fast convolution (image classification)
https://www.zhihu.com/question/53727257

NASNet: automatic structure (object detection)
https://kknews.cc/tech/v8m2yl4.html

capsule
https://www.zhihu.com/question/67287444
https://zhuanlan.zhihu.com/p/30521353
https://zhuanlan.zhihu.com/p/30970675

forward-forward
https://www.zhihu.com/question/570153849/answer/2787026263

rts game
https://github.com/facebookresearch/ELF

CNNMRF: markov random field (image synthesis)
https://github.com/chuanli11/CNNMRF

encoder–decoder + ResNet + GAN (image synthesis)
https://www.zhihu.com/question/67483407

generative query network  2D to 3D + 2D query
https://deepmind.com/blog/neural-scene-representation-and-rendering/

Glow: Generative Flow with Invertible 1x1 Convolutions
https://blog.openai.com/glow/
https://www.jiqizhixin.com/articles/2018-07-13-4
http://akosiorek.github.io/ml/2018/04/03/norm_flows.html

GANimation (face-to-face)
https://zhuanlan.zhihu.com/p/41029562

GANpaint: correlation vs. causation (image synthesis)
http://gandissect.csail.mit.edu/

GauGAN: affine layer (image synthesis)
http://mingyuliutw.github.io/publication.html

Transformer/BERT: attention (nl translation)
https://www.zhihu.com/question/61077555
http://blog.csdn.net/mijiaoxiaosan/article/details/73251443
https://www.zhihu.com/question/36591394
https://github.com/google-research/bert

U-Net: encoder-decoder (medical image segmentation)
https://zhuanlan.zhihu.com/p/57530767

DETR: set prediction (object detection)
https://zhuanlan.zhihu.com/p/366938351

NeRF: MLP (graphics ray marching)
https://blog.csdn.net/ftimes/article/details/105890744

Imagen/Imagic: diffusion model (text-to-image)
https://www.zhihu.com/question/530608581/answer/2608721843
https://lilianweng.github.io/posts/2021-07-11-diffusion-models/
https://theaisummer.com/diffusion-models/

OmniHuman: multi-stage (one-shot video generation)
https://omnihuman-lab.github.io/

realtime

YOLO (object detection)
https://github.com/WongKinYiu/yolov7

YOLACT (instance segmentation)
https://github.com/dbolya/yolact

overview
http://chuansong.me/n/1858260551524

pix2pix   (image to image translation)
https://phillipi.github.io/pix2pix/

StackGAN  (image synthesis)
https://github.com/hanzhanggit/StackGAN

StyleGAN  (generative image modeling)
https://github.com/NVlabs/stylegan
https://github.com/NVlabs/stylegan2

CycleGAN  (image to image translation)
https://github.com/junyanz/CycleGAN

SeqGAN    (nl synthesis)
https://zhuanlan.zhihu.com/p/23326430

IRGAN     (nl reasioning)
http://www.sohu.com/a/144843447_473283

S^3GAN    (photo synthesis)
https://github.com/google/compare_gan

DragGAN   (image sythesis and optical flow)
https://github.com/Zeqiang-Lai/DragGAN

statistics🚧

statistics

統計學基礎問題。

https://tcs.nju.edu.cn/wiki/index.php?title=概率论与数理统计_(Spring_2025)

conditional probability 只關注某一塊子集合  代入身分建立視點
Bayes' theorem 切換視點
independence 即便到了子集合裡面比例也一樣，換句話說，在宇集合內很均勻
             p_xy(x,y) = p_x|y(x,y) p_y(y) = p_x(x) p_y(y)
             p_x|y(x,y) = p_x(x)
correlation 正比反比關係
causation   因果關係
association 上述所有東西的泛稱

normal distribution

central limit theorem 加在一起，平均數接近常態分布
Lévy–Cramér theorem 多個獨立變數，當總和是常態分布，則各自是常態分布
Darmois–Skitovitch theorem 線性組合互相獨立，必是常態分布

martingale

一個隨機過程，最新的K個隨機變數，期望值是定值。

https://en.wikipedia.org/wiki/Doob_martingale
https://en.wikipedia.org/wiki/Azuma's_inequality

When analyzing sums, random walks, or other additive functions of independent
random variables, one can often apply the central limit theorem, law of large
numbers, Chernoff's inequality, Chebyshev's inequality or similar tools. When
analyzing similar objects where the differences are not independent, the main
tools are martingales and Azuma's inequality.

Azuma's inequality applied to the Doob martingale gives the method of bounded
differences (MOBD) which is common in the analysis of randomized algorithms.

concentration

一個隨機變數，實際取樣集中於平均值附近。

generated by ChatGPT。

https://en.wikipedia.org/wiki/Concentration_inequality
https://en.wikipedia.org/wiki/Concentration_of_measure

concentration inequality

Markov's inequality:
Gives an upper bound on the probability that a
non-negative random variable exceeds a certain value.

Chebyshev's inequality:
Provides a bound on how much a random variable
deviates from its mean, in terms of its variance.

Chernoff bounds:
Provide exponentially decreasing bounds on the tail
probabilities of sums of independent random variables.

Hoeffding's inequality:
Gives a concentration bound for the sum of
bounded independent random variables.

concentration of measure

Chernoff Bound:
Gives exponential decay bounds for the tail probabilities
of sums of independent random variables,
often used in concentration of measure results.

McDiarmid's Inequality:
Provides concentration bounds for functions of independent random variables, stating that a function of independent
variables is unlikely to deviate too far from its expected
value if each variable has only a small effect on the function.

Gaussian concentration:
For Gaussian distributions,
the concentration of measure shows that the probability
that a Gaussian random variable deviates by more than
a fixed amount from its mean is exponentially small.