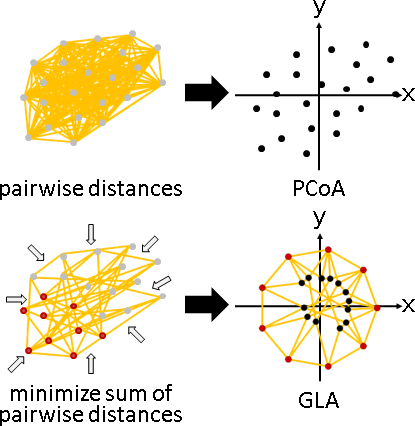
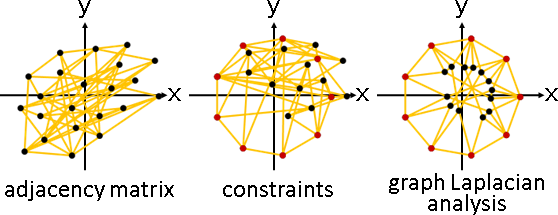
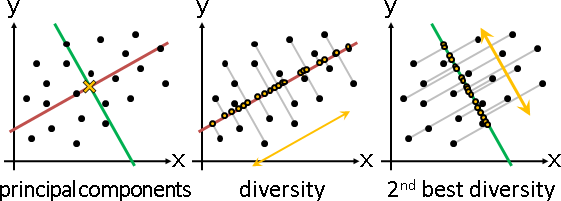
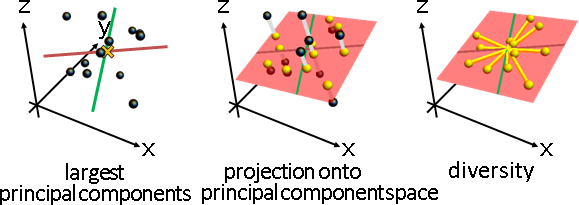
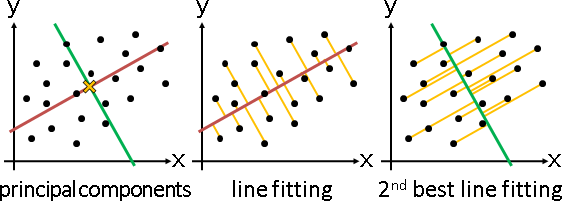
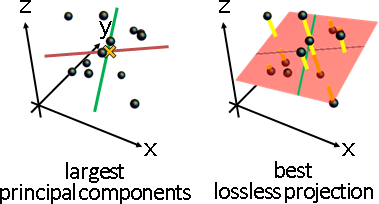
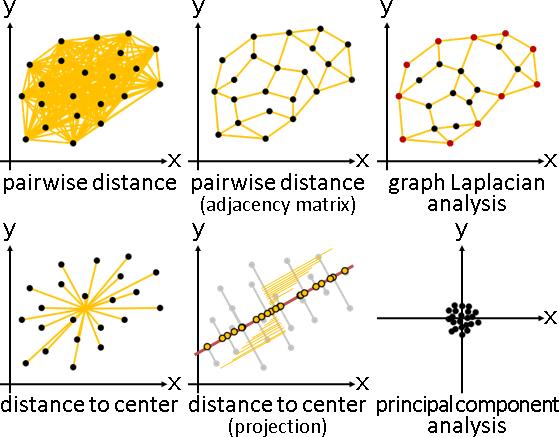
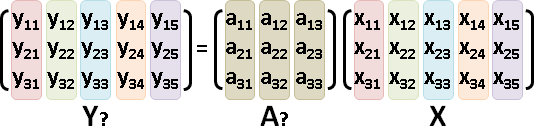
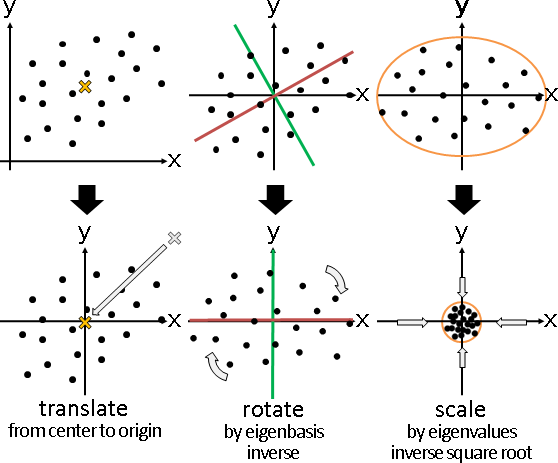
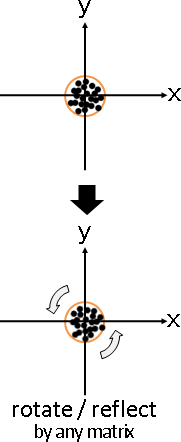
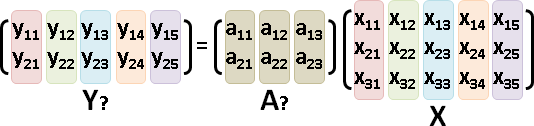
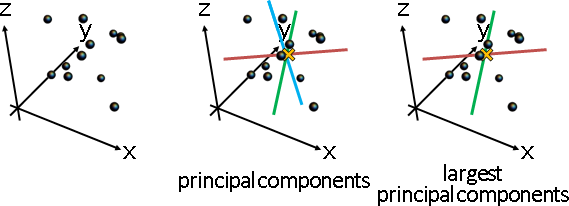
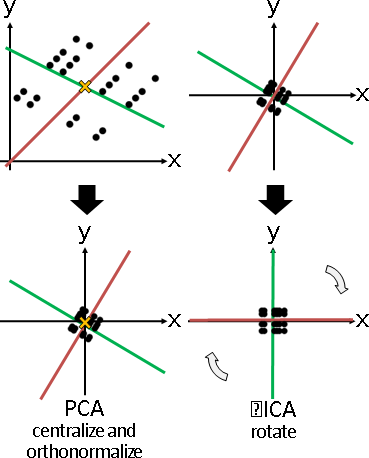
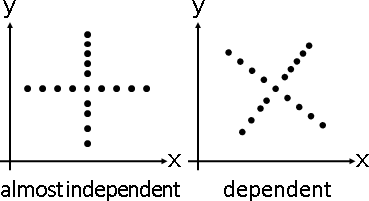
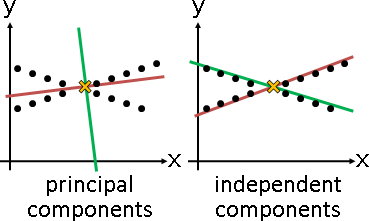
principal coordinate analysis
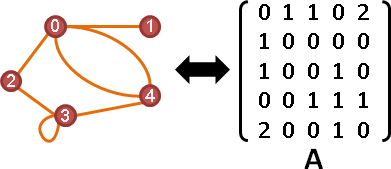
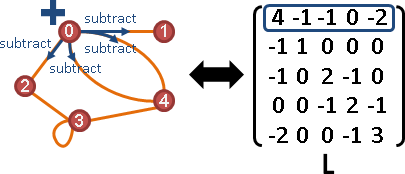
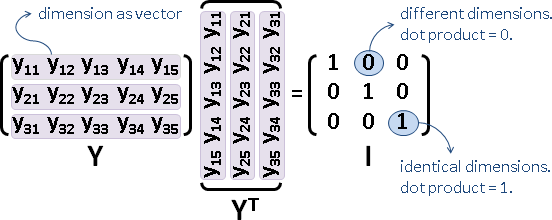
Gram matrix
「點積矩陣」。儲存兩兩點積,元素Aᵢⱼ是i點與j點的點積。
⎡ p₀∙p₀ p₀∙p₁ p₀∙p₂ p₀∙p₃ ... ⎤
⎢ p₁∙p₀ p₁∙p₁ p₁∙p₂ p₁∙p₃ ... ⎥
G = ⎢ p₂∙p₀ p₂∙p₁ p₂∙p₂ p₂∙p₃ ... ⎥
⎢ p₃∙p₀ p₃∙p₁ p₃∙p₂ p₃∙p₃ ... ⎥
⎣ : : : : ⎦
給定數據矩陣,求得點積矩陣:對稱半正定矩陣XᵀX。
⎡ | | ⎤ ⎡ ⎤⎡ | ⎤ ⎡ : ⎤
X = ⎢ p₀ p₁ .. ⎥ XᵀX = ⎢ —— pᵢ —— ⎥⎢ pⱼ ⎥ = ⎢.. pᵢ∙pⱼ ..⎥
⎣ | | ⎦ ⎣ ⎦⎣ | ⎦ ⎣ : ⎦
給定點積矩陣,求得數據矩陣:答案無限多個,例如特徵分解的共軛分解X = √ΛEᵀ、Cholesky分解的共軛分解X = Lᵀ。
eigendecomposition: Cholesky decomposition: XᵀX = EΛEᵀ XᵀX = LLᵀ XᵀX = E√Λ√ΛEᵀ = (√ΛEᵀ)ᵀ√ΛEᵀ X = Lᵀ X = ⟌XᵀX = √ΛEᵀ
註:共軛分解的數學符號⟌,我自己瞎掰的。
distance matrix
「距離矩陣」。儲存兩兩距離,元素Aᵢⱼ是i點與j點的距離。
⎡ ‖p₀-p₀‖ ‖p₀-p₁‖ ‖p₀-p₂‖ ‖p₀-p₃‖ ... ⎤
⎢ ‖p₁-p₀‖ ‖p₁-p₁‖ ‖p₁-p₂‖ ‖p₁-p₃‖ ... ⎥
M = ⎢ ‖p₂-p₀‖ ‖p₂-p₁‖ ‖p₂-p₂‖ ‖p₂-p₃‖ ... ⎥
⎢ ‖p₃-p₀‖ ‖p₃-p₁‖ ‖p₃-p₂‖ ‖p₃-p₃‖ ... ⎥
⎣ : : : : ⎦
給定數據矩陣,求得距離矩陣:利用全一矩陣。
每項平方 X⊙X 橫條平方和 (X⊙X)𝟏 = ‖pᵢ‖² 直條平方和 𝟏(X⊙X) = ‖pⱼ‖² 兩兩點積 XᵀX = (pᵢ ∙ pⱼ) 兩兩距離平方 (X⊙X)𝟏 + 𝟏(X⊙X) - 2(XᵀX) = M⊙M ‖pᵢ‖² + ‖pⱼ‖² - 2(pᵢ ∙ pⱼ) = ‖pᵢ - pⱼ‖² 每項開根號 √[(X⊙X)𝟏 + 𝟏(X⊙X) - 2(XᵀX)]ᵢⱼ = Mᵢⱼ
給定距離矩陣,求得數據矩陣:利用中心化矩陣。
兩兩距離 Mᵢⱼ = ‖pᵢ - pⱼ‖ 每項平方 M⊙M = ‖pᵢ - pⱼ‖² = ‖pᵢ‖² + ‖pⱼ‖² - 2(pᵢ ∙ pⱼ) 行列中心化 C(M⊙M)C = -2(pᵢ ∙ pⱼ) = -2XᵀX 除以負二 -½C(M⊙M)C = (pᵢ ∙ pⱼ) = XᵀX 共軛分解 ⟌-½C(M⊙M)C = X
證明:行列中心化
距離平方矩陣Mᵢⱼ² = ‖pᵢ‖² + ‖pⱼ‖² - 2(pᵢ ∙ pⱼ)。
試證:橫條中心化、直條中心化,可以消去平方項‖pᵢ‖²和‖pⱼ‖²,留下交叉項-2(pᵢ ∙ pⱼ)。
一、中心化可以消去平方項。
橫條擁有相同‖pᵢ‖²。各個橫條各自減去平均數,可以消去‖pᵢ‖²。橫條中心化消去橫條平方項。同理,直條中心化消去直條平方項。
⎡ ‖p₀‖²+‖p₀‖²-2(p₀∙p₀) ‖p₀‖²+‖p₁‖²-2(p₀∙p₁) ... ⎤
⎢ ‖p₁‖²+‖p₀‖²-2(p₁∙p₀) ‖p₁‖²+‖p₁‖²-2(p₁∙p₁) ... ⎥
M⊙M = ⎢ ‖p₂‖²+‖p₀‖²-2(p₂∙p₀) ‖p₂‖²+‖p₁‖²-2(p₂∙p₁) ... ⎥
⎢ ‖p₃‖²+‖p₀‖²-2(p₃∙p₀) ‖p₃‖²+‖p₁‖²-2(p₃∙p₁) ... ⎥
⎣ : : ⎦
^^^^^ ^^^^^
二、中心化也會改變交叉項。
但是我們需要交叉項。解決方法:假設數據已經中心化。
此時數據任一維度總和為零∑pⱼ = 0,使得橫條交叉項總和為零∑ⱼ(-2(pᵢ ∙ pⱼ)) = -2(pᵢ ∙ (∑pⱼ)) = 0。橫條中心化不改變橫條交叉項。同理,直條中心化不改變直條交叉項。
⎡ ‖p₀‖²+‖p₀‖²-2(p₀∙p₀) ‖p₀‖²+‖p₁‖²-2(p₀∙p₁) ... ⎤
⎢ ‖p₁‖²+‖p₀‖²-2(p₁∙p₀) ‖p₁‖²+‖p₁‖²-2(p₁∙p₁) ... ⎥
M⊙M = ⎢ ‖p₂‖²+‖p₀‖²-2(p₂∙p₀) ‖p₂‖²+‖p₁‖²-2(p₂∙p₁) ... ⎥
⎢ ‖p₃‖²+‖p₀‖²-2(p₃∙p₀) ‖p₃‖²+‖p₁‖²-2(p₃∙p₁) ... ⎥
⎣ : : ⎦
^^^^^^^^^ ^^^^^^^^^
三、橫條中心化、直條中心化,無論誰先做,結果都一樣。
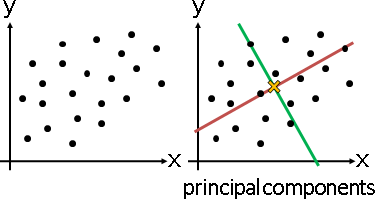
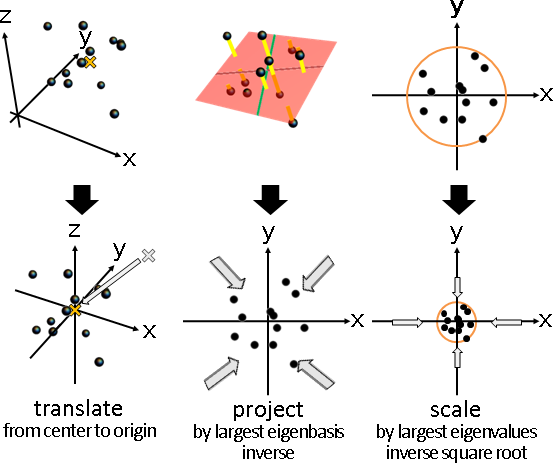
principal coordinate analysis
「主座標分析」。已知距離矩陣,求得數據矩陣。
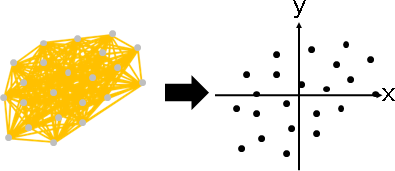
方才已介紹。換句話說吧。
一、距離矩陣M,每項平方,求得距離平方矩陣M⊙M。 二、距離平方矩陣M⊙M,橫條中心化,直條中心化,除以-2,求得點積矩陣XᵀX。 三、點積矩陣XᵀX,共軛分解,求得數據矩陣X。
low-rank principal coordinate analysis
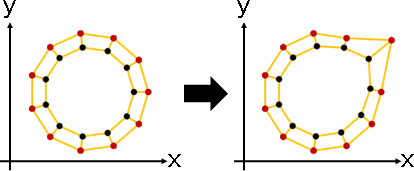
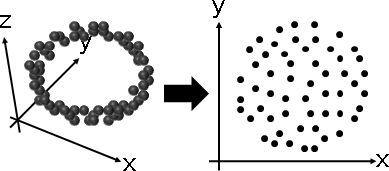
「低秩主座標分析」。已知距離矩陣,求得數據矩陣。降低數據維度,盡量保持原本距離。
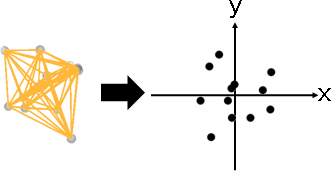
p = {{-0.0561955,-0.00847422,0.453698},{-0.334564,-0.272408,-0.238724},{-0.567886,0.0607641,0.265588},{0.502573,-0.344719,-0.296151},{0.19767,0.450711,0.0407837},{-0.0795941,-0.316957,-0.129278},{0.388671,0.00273937,0.330277},{0.0718672,-0.0904262,0.213121},{0.0928513,-0.312574,0.213095},{0.0484546,0.251097,-0.522902},{0.0447417,0.575007,-0.0364518},{-0.308589,0.00523944,-0.293056}}; a = Flatten[Table[Table[p[[i]], Length[p]], {i, Length[p]}], 1]; b = Flatten[Table[p, Length[p]], 1]; l = Transpose[{a,b}]; Graphics3D[{Black, Specularity[White, 10], Opacity[0.2], Sphere[p, 0.05], Thickness[0.01], CapForm["Butt"], RGBColor[255,192,0], Opacity[0.9], Line[l]}, PlotRange -> {{-.6,.6},{-.6,.6},{-.6,.6}}, Boxed -> False] o = Mean[p]; p = p - Table[o, Length[p]]; G = p . Transpose[p]; e = Eigenvectors[N[G], 2]; v = Eigenvalues[N[G], 2] q = Transpose[DiagonalMatrix[v] . e]; Graphics[{Black, PointSize[0.05], Point[q]}, PlotRange -> {{-.6,.6},{-.6,.6},{-.6,.6}}, Boxed -> False]
修改最後一步。點積矩陣,保留前k大的特徵值們,其餘歸零。特徵分解的右半邊√ΛEᵀ,即是k維數據矩陣。
「low-rank matrix approximation」的最佳解是奇異值分解。點積矩陣是對稱半正定矩陣,於是奇異值分解等同特徵分解。
降維對象是點積矩陣。為何不是距離矩陣呢?這是一個謎,等你發表論文。先中心化再低秩,先低秩再中心化,兩者結果應該不同。
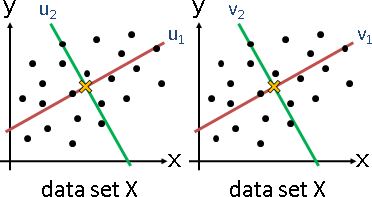
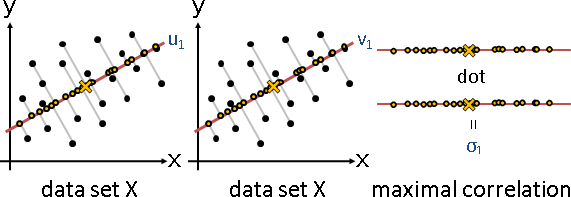
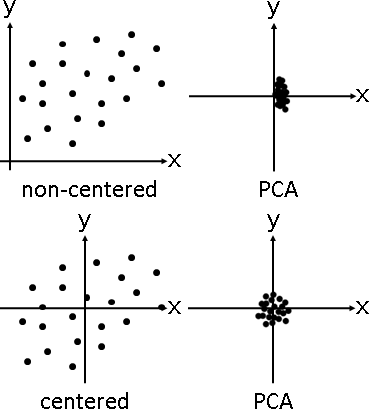
multidimensional scaling
「多維度縮放」。已知原始數據,求得降維數據,盡量保持原本距離。
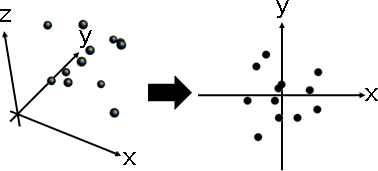
求解步驟較少,不必求得距離矩陣、點積矩陣。
數據矩陣中心化。數據矩陣,保留前k大的奇異值們,其餘歸零。奇異值分解的右半邊ΣVᵀ,即是k維數據矩陣。
XᵀX即是點積矩陣。XᵀX的特徵向量,即是X的右奇異向量。XᵀX的特徵值開根號,即是X的奇異值。√ΛEᵀ = ΣVᵀ。