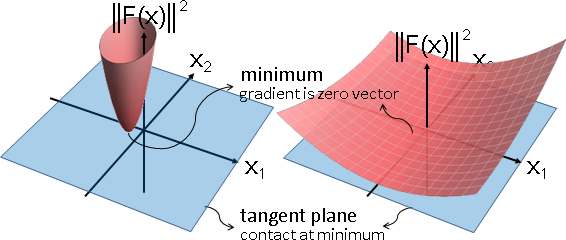
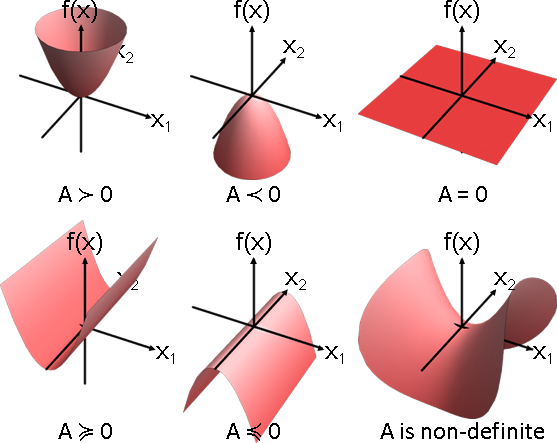
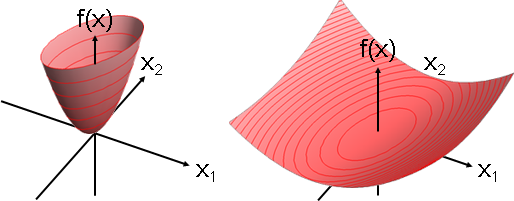
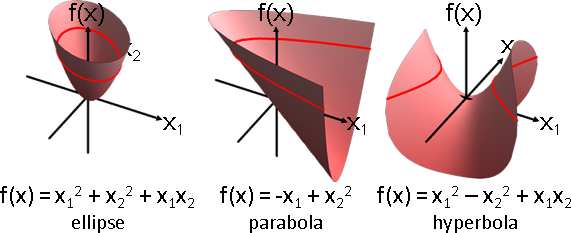
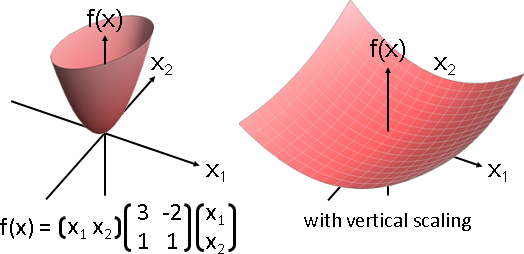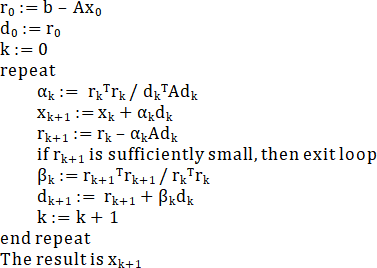人為加工
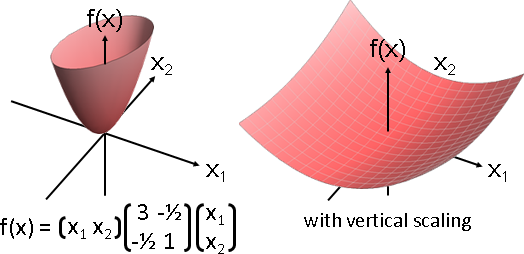
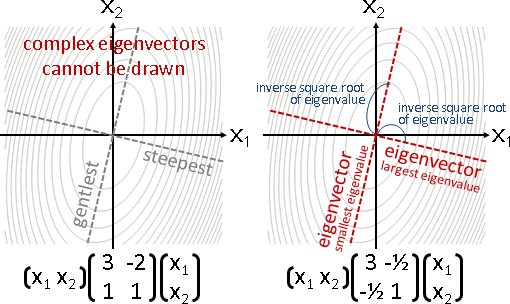
二次最佳化的主要用途是一次方程組求解。當A是對稱正定矩陣,f(x) = 1/2 xᵀAx - bᵀx的最小值位置,即是Ax = b的解。
(正定確保唯一解,對稱確保形成A。)
a unique solution exist
argmin f(x) <=======================> solve f′(x) = 0
let f(x) = 1/2 xᵀAx - bᵀx
f′(x) = 1/2 (A+Aᵀ)x - b
argmin 1/2 xᵀAx - bᵀx
---> solve 1/2 (A+Aᵀ)x - b = 0 (A is positive definite)
---> solve Ax = b (A is symmetric)
這導致世上所有的二次最佳化演算法,全部都是針對f(x) = 1/2 xᵀAx - bᵀx,而非f(x) = xᵀAx + bᵀx + c。非常奇葩。
想要最佳化標準的二次函數f(x) = xᵀAx + bᵀx + c,記得先將A乘以2、將b變號、將c刪掉,才能實施下述演算法。
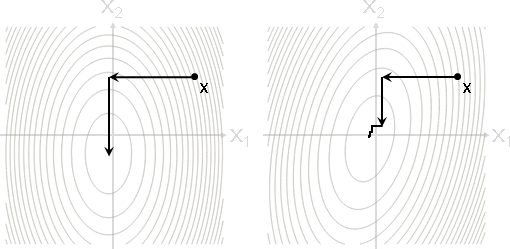
coordinate descent method(座標下降法)
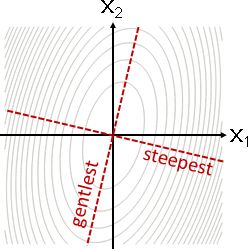
朝著座標軸方向,正向逆向皆可,一步走到最低處。然後輪到下一個座標軸。
橢圓軸線與座標軸方位相同:最多N步,必定抵達最小值。
橢圓軸線與座標軸方位不相同:無限多步,逐步趨近最小值。
ContourPlot[3*x*x + y*y + x + y + 1, {x, -3, 3}, {y, -3, 3}, Frame -> False, ContourShading -> None, Contours -> 21]
總而言之,應該要往其他方向走。
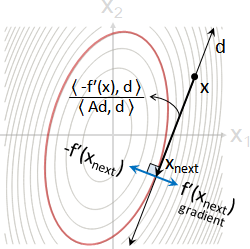
line search(直線搜尋)
給定地點x,給定前進方向d,正向逆向皆可,請一步走到該方向的最低處xnext。
畫成圖形就是等高線的切線d和切點xnext。
ContourPlot[(3x-2y)*x + (x+y)*y + x + 1, {x, -3, 3}, {y, -3, 3}, Frame -> False, ContourShading -> None, Contours -> 21]
也就是說,最低處的梯度方向f′(xnext) = Axnext - b、行進方向d,互相垂直,點積是零。
藉此推導步伐大小α = ⟨-f′(x) , d⟩ / ⟨Ad , d⟩。
數學公式:
α = ⟨-f′(x) , d⟩ / ⟨Ad , d⟩
= ⟨b - Ax , d⟩ / ⟨Ad , d⟩
xnext = x + α d
d: direction
α: step size
f′(x): gradient at position x (normally ∇f(x))
⟨a,b⟩: dot product of vector a and b (normally a∙b)
演算法步驟:
x = random vector
while (true)
{
d = get_direction(x);
α = ⟨b - Ax , d⟩ / ⟨Ad , d⟩
if (α < ε) return x
x = x + α d
}
延伸閱讀:推導過程
f(x) = 1/2 xᵀAx - bᵀx
f′(x) = Ax - b
⎰ xnext = x + α d
⎱ α = argmin f(x + α d)
⟨f′(xnext) , d⟩ = 0 perpendicularity
⟨f′(x + α d) , d⟩ = 0 substitution
⟨A(x + α d) - b , d⟩ = 0 substitution
⟨Ax + α Ad - b , d⟩ = 0 expansion
⟨Ax - b + α Ad , d⟩ = 0 arrangement
⟨Ax - b , d⟩ + α ⟨Ad , d⟩ = 0 distributive law
α = - ⟨Ax - b , d⟩ / ⟨Ad , d⟩ transposition
α = ⟨b - Ax , d⟩ / ⟨Ad , d⟩ arrangement
α = ⟨-f′(x) , d⟩ / ⟨Ad , d⟩ just a coincidence
steepest descent method(最陡下降法)
承上,仔細規定每一步的前進方向:梯度反方向(朝向低處)。
d = -f′(x) = b - Ax
α = ⟨d , d⟩ / ⟨Ad , d⟩
xnext = x + α d
由於人為加工,梯度反方向-f′(x) = b - Ax碰巧等於殘差r = b - Ax。有些書籍將前進方向d改寫成殘差r,看上去比較帥氣。
r = b - Ax
α = ⟨r , r⟩ / ⟨Ar , r⟩
xnext = x + α r
r: residual (equal to negative gradient. just a coincidence.)
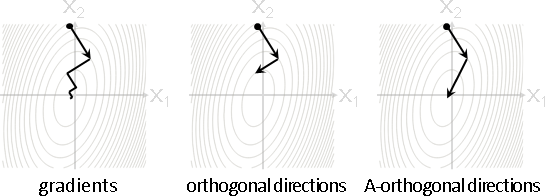
conjugate direction method(共軛方向法)
承上,仔細規定每一步的前進方向:互相傍A垂直。
一、前後垂直 ⟨dᵢ , dᵢ₊₁⟩ = 0:逐步趨近最小值。
二、互相垂直 ⟨dᵢ , dⱼ ⟩ = 0:最多N步,通常無法抵達最小值。
三、互相傍A垂直⟨dᵢ , Adⱼ ⟩ = 0:最多N步,必定抵達最小值。
第一種方式是「最陡下降法」。第三種方式是「共軛方向法」。
挑選N個前進方向,互相傍A垂直,有無限多種方式。步伐大小符合直線搜尋,就能保證N步抵達最小值。
挑選N個前進方向,一種方式是Krylov subspace聯合Gram–Schmidt orthonormalization,將v, Av, A²v, A³v, ..., Aᴺ⁻¹v扳成互相傍A垂直,邊走邊扳。v可以是任意向量,實務上是b。
共軛方向法和Cholesky分解的時間複雜度都是O(N³),但是共軛方向法可以逐步趨近最小值。實務上,共軛方向法只取足夠精確度,得以取消最後幾步,進而縮短時間,優於Cholesky分解。
共軛方向法跟共軛毫無關聯!論文作者誤以為「傍A垂直A-orthogonal」可以稱作「共軛conjugate」。大家將錯就錯。
數學公式:
α = ⟨d , -g⟩ / ⟨d , A d⟩
xnext = x + α d
gnext = g + α A d
dnext = A-orthonomalize(A d)
g: gradient f′(x) = Ax - b
r: residual -f′(x) = b - Ax
演算法步驟:
x₀ = random vector // initial position
g₀ = f′(x₀) = Ax₀ - b // initial gradient
d₀ = random vector // initial direction
d₀ = d₀ / ‖d₀‖ // normalization
if (‖g₀‖ < ε) return x₀ // ‖g₀‖ = sqrt(⟨g₀, g₀⟩)
for (k = 0 ... n-1) // loop all dimensions
{
αk = ⟨dk, -gk⟩ / ⟨dk, A dk⟩ // update step size
xk+1 = xk + αk dk // update position
gk+1 = gk + αk A dk // update gradient
if (‖gk+1‖ < ε) return xk+1 // ‖gk+1‖ = sqrt(⟨gk+1, gk+1⟩)
dk+1 = A dk // update direction
for (t = 0 ... k) // A-orthonormalization
dk+1 -= ⟨dk+1, A dt⟩ dt
dk+1 = dk+1 / ‖dk+1‖ // normalization
}
return xk+1
延伸閱讀:推導過程
一、最小值位置x*的性質:位於一次微分等於零的地方。
f′(x*) = Ax* - b = 0
二、誤差e = x* - x的性質:誤差經過A變換,碰巧是梯度反方向。
Ae = Ax* - Ax = (Ax* - b) - (Ax - b) = f′(x*) - f′(x) = -f′(x)
三、前進方向d的性質:前進方向互相傍A垂直。
⟨dᵢ, Adⱼ⟩ = 0
四、前進方向d的性質:若前進方向互相傍A垂直,則線性獨立。
A-orthogonal directions are linear independent
proof by contradiction
assume dₖ = c₀d₀ + c₁d₁ + ... + cₖ₋₁dₖ₋₁ is not linear independent
1. ⟨dₖ , Adₖ⟩ = c₀ ⟨d₀ , Adₖ⟩ + ... + cₖ₋₁ ⟨dₖ₋₁ , Adₖ⟩ = 0
(A-orthogonal directions)
2. ⟨dₖ , Adₖ⟩ > 0
(A is symmetric positive definite and dₖ ≠ 0)
五、任意向量v的性質:若前進方向互相線性獨立,則N步必能形成任意向量。
v = c₀d₀ + c₁d₁ + ... + cɴ₋₁dɴ₋₁
六、初始誤差e₀ = x* - x₀的性質:N步必能走到最佳解。步伐大小α。
e₀ = α₀d₀ + α₁d₁ + ... + αɴ₋₁dɴ₋₁
七、步伐大小α的性質:恰好等同直線搜尋。
e₀ = α₀d₀ + α₁d₁ + ... + αɴ₋₁dɴ₋₁
Ae₀ = A(α₀d₀ + α₁d₁ + ...)
⟨d₀ , Ae₀⟩ = ⟨d₀ , A(α₀d₀ + α₁d₁ + ...)⟩
⟨d₀ , Ae₀⟩ = α₀ ⟨d₀ , Ad₀⟩ + α₁ ⟨d₀, Ad₁⟩ + ...
⟨d₀ , Ae₀⟩ = α₀ ⟨d₀ , Ad₀⟩
α₀ = ⟨d₀, Ae₀⟩ / ⟨d₀, Ad₀⟩
α₀ = ⟨d₀, -f′(x₀)⟩ / ⟨d₀, Ad₀⟩ line search
similarly,
consider Ae₁ and get α₁ = ⟨d₁, -f′(x₁)⟩ / ⟨d₁, Ad₁⟩
consider Ae₂ and get α₂ = ⟨d₂, -f′(x₂)⟩ / ⟨d₂, Ad₂⟩
:
八、N處梯度g的性質:梯度遞推公式gnext = g + α A d。
g₁ - g₀ = f′(x₁) - f′(x₀) = -Ae₁ + Ae₀ = A(-e₁ + e₀)
= A(x₁ - x* + x* - x₀) = A(x₁ - x₀) = A(α₀ d₀) = α₀ A d₀
g₁ = g₀ + α₀ A d₀
g₂ = g₀ + α₀ A d₀ + α₁ A d₁
g₃ = g₀ + α₀ A d₀ + α₁ A d₁ + α₂ A d₂
:
九、N處位置x的性質:第k步走到當前最佳解(考慮第k個方向能夠觸及的所有位置)。
N處位置x的性質:頭k步走到當前最佳解(考慮頭k個方向能夠觸及的所有位置)。
證明省略。
xk is the optimal solution of min f(x) when x ∈ Dk
D₀ = span(d₀) = span(v)
x₁ = x₀ + α₀d₀ = argmin { f(x) : x ∈ D₀ }
D₁ = span(d₀, d₁) = span(v, Av)
x₂ = x₀ + α₀d₀ + α₁d₁ = argmin { f(x) : x ∈ D₁ }
D₂ = span(d₀, d₁, d₂) = span(v, Av, A²v)
x₃ = x₀ + α₀d₀ + α₁d₁ + α₂d₂ = argmin { f(x) : x ∈ D₂ }
:
十、N處梯度g的性質:垂直於先前所有方向。
證明省略。
g₁ ⟂ D₀ = span(d₀)
g₂ ⟂ D₁ = span(d₀, d₁)
g₃ ⟂ D₂ = span(d₀, d₁, d₂)
:
conjugate gradient method(共軛梯度法)
承上,仔細規定拿來扳正的向量:梯度反方向。
一、任意向量v。v, Av, A²v, A³v, ..., Aᴺ⁻¹v,扳成互相傍A垂直。
二、N個位置的梯度反方向-f′(x₀) ... -f(xɴ₋₁),扳成互相傍A垂直。
第一種方式是「共軛方向法」。第二種方式是「共軛梯度法」。
邊走邊扳。利用遞推公式,製造每一步的前進方向:本次梯度反方向、上次前進方向,兩者的加權平均數,作為本次前進方向。
邊走邊扳。N個位置的梯度反方向,扳正之後所得到的N個行進方向,恰巧導致這N個梯度互相垂直!遞推公式可以稍作簡化!
也就是說,共軛梯度法同時滿足兩個性質:
一、前進方向互相傍A垂直⟨dᵢ , Adⱼ⟩ = 0
二、梯度互相垂直⟨gᵢ , gⱼ⟩ = 0
(殘差互相垂直⟨rᵢ , rⱼ⟩ = 0)
共軛梯度法的時間複雜度也是O(N³),但是計算步驟更少。
數學公式:
α = ⟨g, g⟩ / ⟨d, A d⟩
xnext = x + α d
gnext = g + α A d
β = ⟨gnext, gnext⟩ / ⟨g, g⟩
dnext = -gnext + β d
演算法步驟:
x₀ = random vector // initial position
g₀ = f′(x₀) = Ax₀ - b // initial gradient
d₀ = -g₀ // initial direction
if (‖g₀‖ < ε) return x₀ // ‖g₀‖ = sqrt(⟨g₀, g₀⟩)
for (k = 0 ... n-1) // loop all dimensions
{
αk = ⟨gk, gk⟩ / ⟨dk, A dk⟩ // update step size
xk+1 = xk + αk dk // update position
gk+1 = gk + αk A dk // update gradient
if (‖gk+1‖ < ε) return xk+1 // ‖gk+1‖ = sqrt(⟨gk+1, gk+1⟩)
βk = ⟨gk+1, gk+1⟩ / ⟨gk, gk⟩ // update direction coefficient
dk+1 = -gk+1 + βk dk // update direction
}
return xk+1
演算法步驟(殘差風格),借用一下維基百科的圖片:
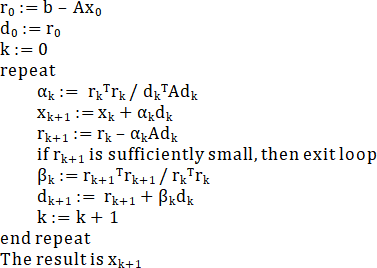
延伸閱讀:推導過程
1. next direction: dk+1
⎰ d0 = -g0 // negative gradient goto minimum
⎱ dk+1 = -gk+1 + βk dk // adaptive gradient descent
2. a special formula: ⟨dk , gk⟩ = ⟨-gk , gk⟩
⎰ dk+1 = -gk+1 + βk dk // adaptive gradient descent
⎱ ⟨dk , gk+1⟩ = 0 // line search
⟨dk+1 , gk+1⟩ = ⟨-gk+1 , gk+1⟩ + βk ⟨dk , gk+1⟩
⟨dk+1 , gk+1⟩ = ⟨-gk+1 , gk+1⟩
⟨dk , gk⟩ = ⟨-gk , gk⟩ // dk = -gk when k = 0
3. alternative step size: αk
αk = ⟨dk , -gk⟩ / ⟨dk , A dk⟩ // line search
αk = ⟨gk , gk⟩ / ⟨dk , A dk⟩ // 2.
4. direction coefficient: βk
⎰ dk+1 = -gk+1 + βk dk // adaptive gradient descent
⎱ ⟨dk+1 , A dk⟩ = 0 // conjugate direction method
⟨dk+1 , A dk⟩ = ⟨-gk+1 , A dk⟩ + βk ⟨dk , A dk⟩
0 = ⟨-gk+1 , A dk⟩ + βk ⟨dk , A dk⟩
βk = ⟨gk+1 , A dk⟩ / ⟨dk , A dk⟩
5. all gradients are orthogonal
5a. gradient gk+1 is orthogonal to direction d₀ ... dk
⟨gk+1 , di⟩ = 0 for i = 0 ... k // conjugate direction method
gk+1 ⟂ Dk = span(d₀, d₁, ..., dk) // conjugate direction method
5b. take all negative gradients for A-orthonormalization
-gi ∈ Dk = span(d₀, d₁, ..., dk) for i = 0 ... k
⟨gi , gk+1⟩ = 0 for i = 0 ... k
6. alternative direction coefficient: βk
βk = ⟨gk+1 , A dk⟩ / ⟨dk , A dk⟩
βk = ⟨gk+1 , αk A dk⟩ / ⟨dk , αk A dk⟩ // expand a fraction
βk = ⟨gk+1 , gk+1 - gk⟩ / ⟨dk , gk+1 - gk⟩ // gradient formula
βk = ⟨gk+1 , gk+1⟩ / ⟨dk , gk+1 - gk⟩ // orthogonal gradients
βk = ⟨gk+1 , gk+1⟩ / ⟨dk , -gk⟩ // line search
βk = ⟨gk+1 , gk+1⟩ / ⟨gk , gk⟩ // 2.