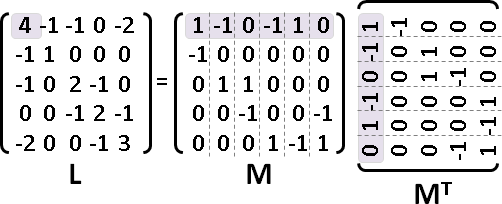adjacency matrix
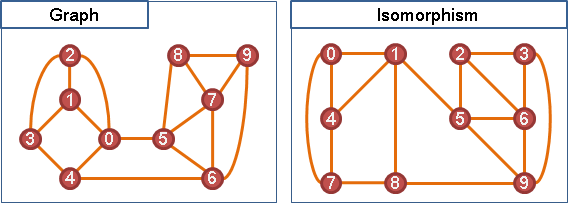
adjacency matrix
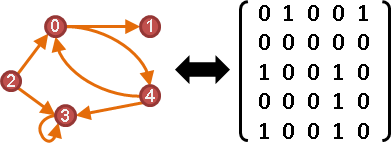
矩陣A。點與點關係。
transpose of adjacency matrix
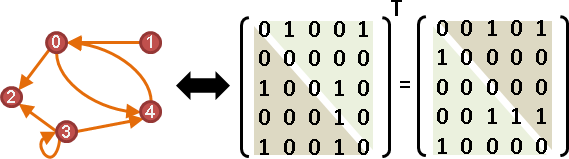
Aᵀ可以翻轉所有邊的方向。
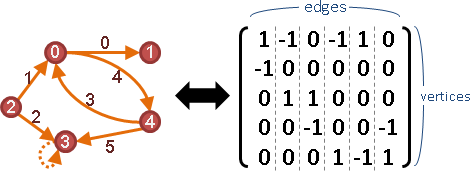
vertex labeling
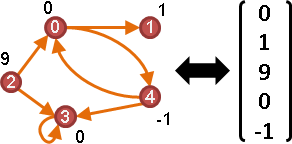
向量x。
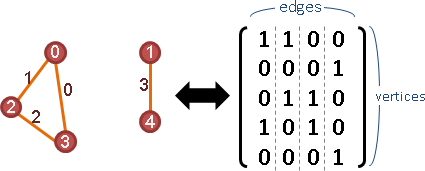
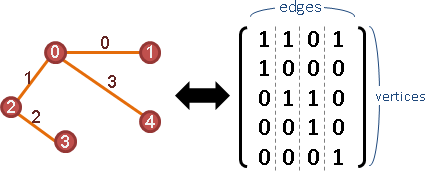
edge labeling
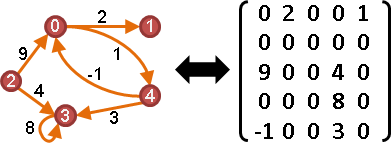
矩陣W。
neighbor
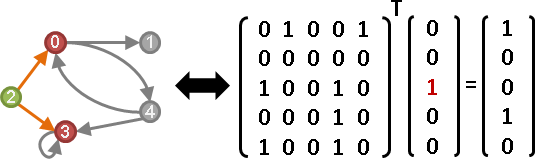
Aᵀx。x的元素們,起點是1,其餘點是0。
元素是布林,元素加法是布林OR,元素乘法是布林AND。
degree
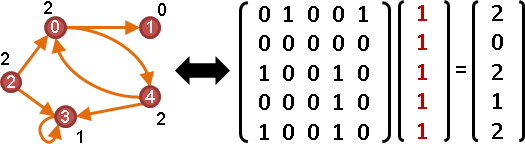
Aᵀx是入邊數量,Ax是出邊數量。x的元素們,通通是1。
元素是實數,元素加法是實數加法,元素乘法是實數乘法。
walk
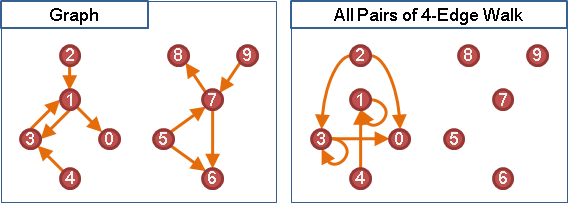
Aᴺ。N是步數。
元素是布林,元素加法是布林OR,元素乘法是布林AND。
矩陣次方,總共O(logN)次矩陣乘法。
矩陣乘法,直接計算O(V³),Strassen's algorithm O(Vω)。
Strassen's algorithm需要用到元素加法反運算,然而布林OR沒有反運算。改弦易轍,以實數代替布林,零當作false,非零當作true。
walk詳細解釋
把一張圖想像成道路地圖,把圖上的點想像成地點,把圖上的邊想像成道路。現在我們在意的是:由某一點開始,走過N條道路後,可以到達哪些點?
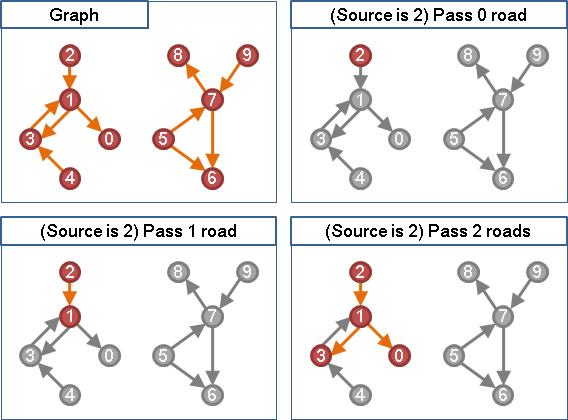
走過零條道路,原地不動。
走過一條道路,跑到隔壁鄰居了。
走過N條道路,各位應該馬上想試試看graph traversal──可是遇到重複地點就沒轍了。graph traversal只能拜訪一個點一次。
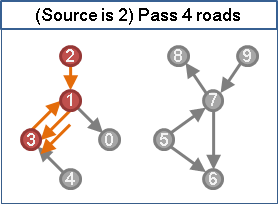
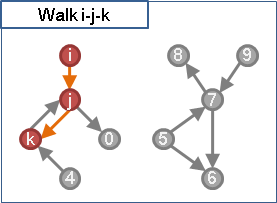
如果i點可以走到某一個j點、這個j點又可以走到k點,那麼就可以由i點走到k點,剛好兩條道路。
窮舉所有可能的j點,就可以判斷i點走到k點,是否剛好兩條道路!
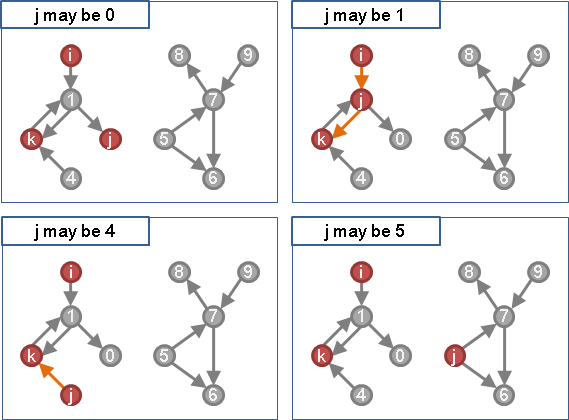
寫成數學式子:
r₂(i, k) = ( r₁(i, 0) AND r₁(0, k) ) OR
( r₁(i, 1) AND r₁(1, k) ) OR
( r₁(i, 2) AND r₁(2, k) ) OR
:
( r₁(i, V-1) AND r₁(V-1, k) )
r₂(i, k):i點走到k點,是否剛好2條道路。
i點到j點,j點到k點,窮舉j點──宛如矩陣乘法求元素(i,k)。一次矩陣乘法就將所有(i,k)配對通通算好。
元素加法是布林OR,元素乘法是布林AND,adjacency matrix自己乘上自己,就是走兩條道路的情況了!
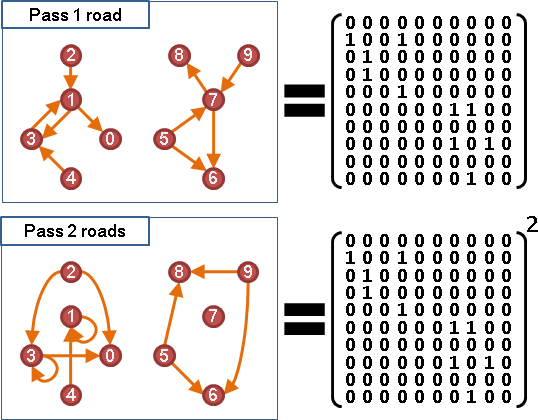
兩條添加一條就是三條,三條添加一條就是四條。逐次添加一條道路,慢慢累積,最後就得到走N條道路的情況。
走兩條道路的矩陣,再乘上一次adjacency matrix,就是走三條道路的矩陣。走N條道路的矩陣,就是N次方。
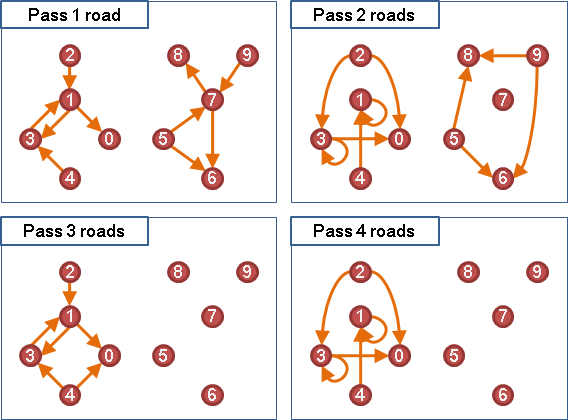
另外這個方法也可以用來計算從一點走到另外一點,走N條道路,總共有幾種走法。各位可以想想看。
UVa 10681
transitive closure
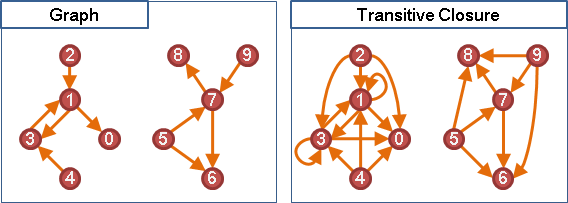
圖上每一個點,可以走到圖上哪些點。
以路徑長度進行分類。每一個點,走零條、走一條、走兩條、……、走無限多條邊,到達圖上哪些點。
A* = I ⋁ A ⋁ A² ⋁ ... ⋁ A∞
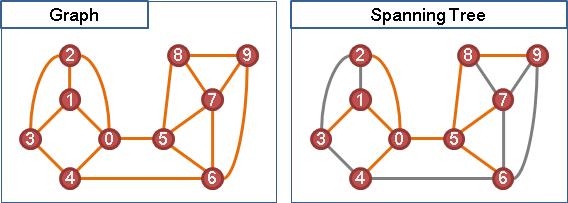
一張圖總共V個點。走路不繞圈子,V-1條邊足矣。
A* = I ⋁ A ⋁ A² ⋁ ... ⋁ AV-1
矩陣多項式,Horner's rule一加一乘。總共O(V)次矩陣乘法與矩陣加法。
(一)以實數代替布林。
A* = I + A + A² + ... + AV-1
矩陣乘法,得以使用Strassen's algorithm O(Vω)。
(二)級數化作分式。
A* = I + A + A² + ... = (I - A)⁻¹
為了收斂,添加一個倍率α,讓α < 1。
A* = I + (αA) + (αA)² + ... = (I - αA)⁻¹
反矩陣,高斯消去法O(V³)。
UVa 12695
strongly connected component
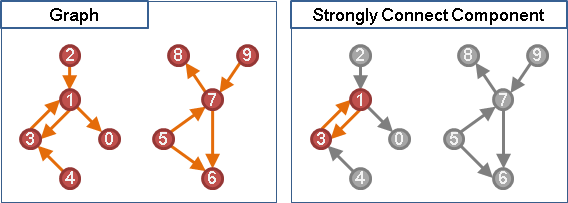
(A* ⋀ A*ᵀ)x。往返,鄰居,一次找一個。
path
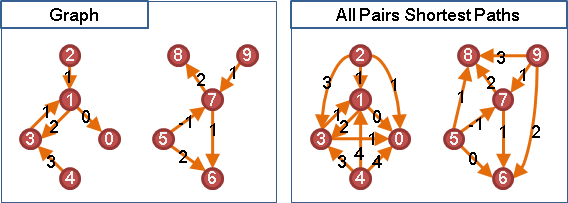
D = ∞I + W + W² + ... + WV-1。
元素是實數,元素加法是實數min,元素乘法是實數加法。
矩陣乘法,然而實數min沒有反運算,必須採用特殊手法避開反運算,例如Seidel's algorithm。
http://theory.stanford.edu/~virgi/cs367/ http://www.lab2.kuis.kyoto-u.ac.jp/keisan-genkai/reports/2006/nhc/Uri_Zwick.pdf http://www.cs.tau.ac.il/~zwick/Adv-Alg-2015/Matrix-Graph-Algorithms.pdf https://resources.mpi-inf.mpg.de/departments/d1/teaching/ss12/AdvancedGraphAlgorithms/Slides14.pdf
circuit
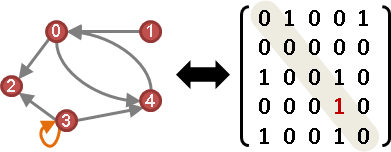
矩陣對角線,即是自環。
矩陣n次方的對角線,即是長度n的迴路。
A¹對角線:一步回到原處。 A²對角線:兩步回到原處。 A³對角線:三步回到原處。
A¹對角線總和:自環數量。 A²對角線總和:邊數的兩倍。(A預先刪除自環) A³對角線總和:三角形數量的六倍。(A預先刪除自環)
tr(A) = L loop number L tr(A²) = 2E when tr(A) = 0 edge number E tr(A³) = 6T when tr(A) = 0 triangle number T
directed acyclic graph
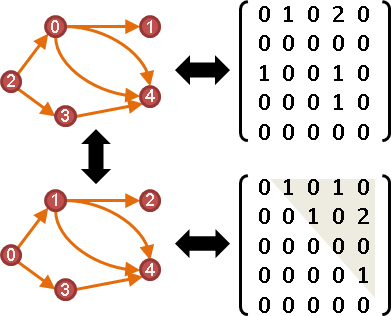
重排編號,重排橫條直條,形成三角矩陣(上下皆可),而且對角線是零。
順帶一提,有向圖可以拆解成一群自環(對角矩陣)、兩個有向無環圖(上下三角矩陣,不含對角線)。重排編號,得到不同拆解方式。
component
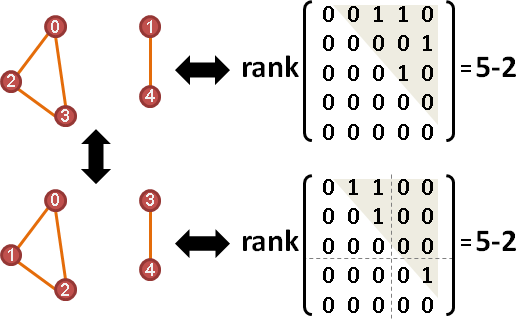
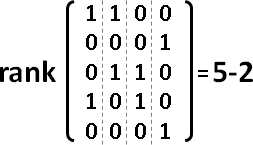
rank(U) = V - C。無向圖的上三角矩陣(不含對角線),矩陣維度=點數-連通分量數量。
換句話說,特徵值為零的數量,等於連通分量數量。
證明手法:重排編號,重排橫條直條,讓連通分量靠在一起,形成分塊矩陣。
matching
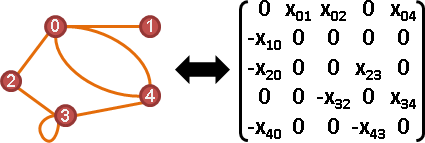
Tutte matrix:權重換成變數。下三角矩陣變號。刪除對角線。
Tᵢⱼ = { xᵢⱼ if i < j and edge (i,j) exists
{ -xⱼᵢ if i > j and edge (i,j) exists
{ 0 otherwise
rank(T):最大匹配的邊數的兩倍。
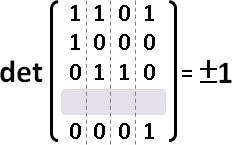
det(T) ≠ 0:完美匹配是否存在。